Chapter 7 Normal Curves and Sampling Distributions Understanding

Chapter 7 Normal Curves and Sampling Distributions Understanding Basic Statistics Fifth Edition By Brase and Brase Prepared by Jon Booze

The Normal Distribution • A continuous distribution used for modeling many natural phenomena. • Sometimes called the Gaussian Distribution, after Carl Gauss. • The defining features of a Normal Distribution are the mean, µ, and the standard deviation, σ. Copyright © Cengage Learning. All rights reserved. 7 | 2
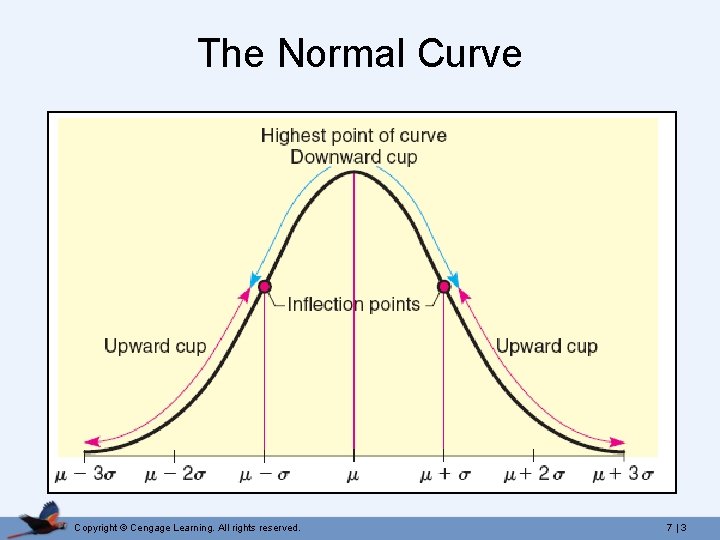
The Normal Curve Copyright © Cengage Learning. All rights reserved. 7 | 3

Features of the Normal Curve • Smooth line and symmetric around µ. • Highest point directly above µ. • The curve never touches the horizontal axis in either direction. • As σ increases, the curve spreads out. • As σ decreases, the curve becomes more peaked around µ. • Inflection points at µ ± σ. Copyright © Cengage Learning. All rights reserved. 7 | 4
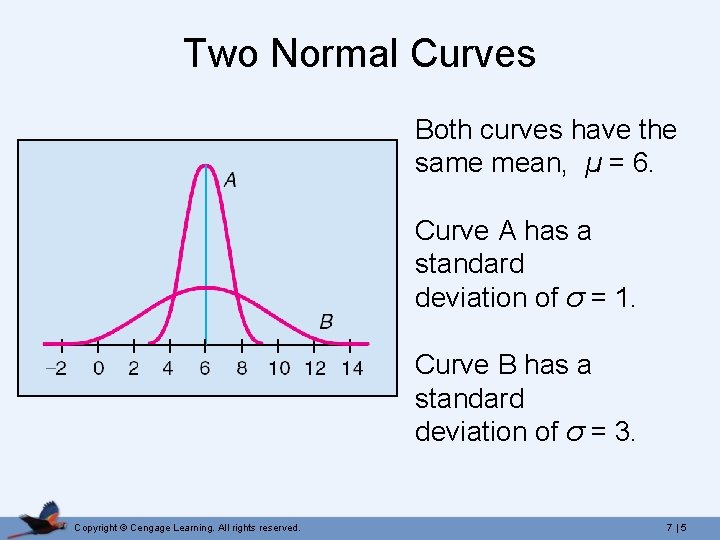
Two Normal Curves Both curves have the same mean, µ = 6. Curve A has a standard deviation of σ = 1. Curve B has a standard deviation of σ = 3. Copyright © Cengage Learning. All rights reserved. 7 | 5

Normal Probability • The area under any normal curve will always be 1. • The portion of the area under the curve within a given interval represents the probability that a measurement will lie in that interval. Copyright © Cengage Learning. All rights reserved. 7 | 6

The Empirical Rule Copyright © Cengage Learning. All rights reserved. 7 | 7
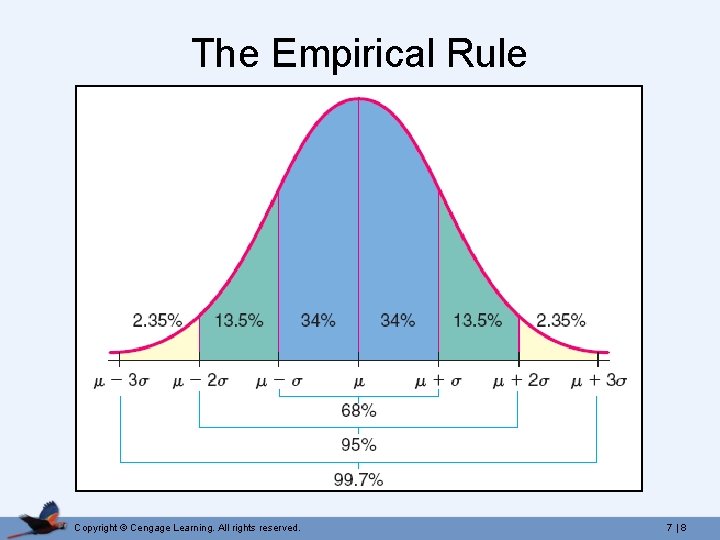
The Empirical Rule Copyright © Cengage Learning. All rights reserved. 7 | 8

The Empirical Rule The masses of the adult ostriches at the Vilas Zoo are normally distributed with a mean of 124 kg and a standard deviation of 10 kg. What is the probability that a randomly-selected ostrich will have a mass between 124 kg and 154 kg? a). 0. 15% b). 99. 85% c). 49. 85% d). 47. 5% Copyright © Cengage Learning. All rights reserved. 7 | 9

The Empirical Rule The masses of the adult ostriches at the Vilas Zoo are normally distributed with a mean of 124 kg and a standard deviation of 10 kg. What is the probability that a randomly-selected ostrich will have a mass between 124 kg and 154 kg? a). 0. 15% b). 99. 85% c). 49. 85% d). 47. 5% Copyright © Cengage Learning. All rights reserved. 7 | 10

Raw Scores and z Scores Copyright © Cengage Learning. All rights reserved. 7 | 11

Raw Scores and z Scores For a distribution with = 10 and = 2. 5, find the z score of the value x = 15. a). z = 2 b). z = 12. 5 c). z = 4 d). z = 3. 16 Copyright © Cengage Learning. All rights reserved. 7 | 12

Raw Scores and z Scores For a distribution with = 10 and = 2. 5, find the z score of the value x = 15. a). z = 2 b). z = 12. 5 c). z = 4 d). z = 3. 16 Copyright © Cengage Learning. All rights reserved. 7 | 13
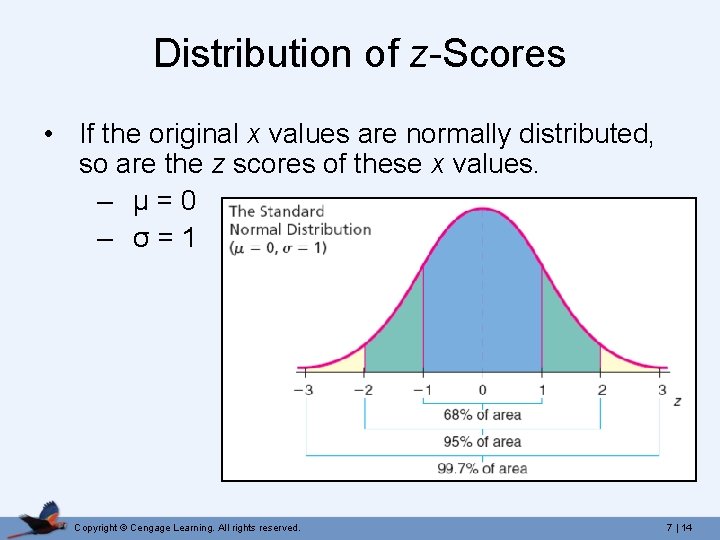
Distribution of z-Scores • If the original x values are normally distributed, so are the z scores of these x values. – µ = 0 – σ = 1 Copyright © Cengage Learning. All rights reserved. 7 | 14

Using the Standard Normal Distribution There are extensive tables for the Standard Normal Distribution. • We can determine probabilities for normal distributions: 1) Transform the measurement to a z score. 2) Utilize Table 3 of the Appendix. Copyright © Cengage Learning. All rights reserved. 7 | 15
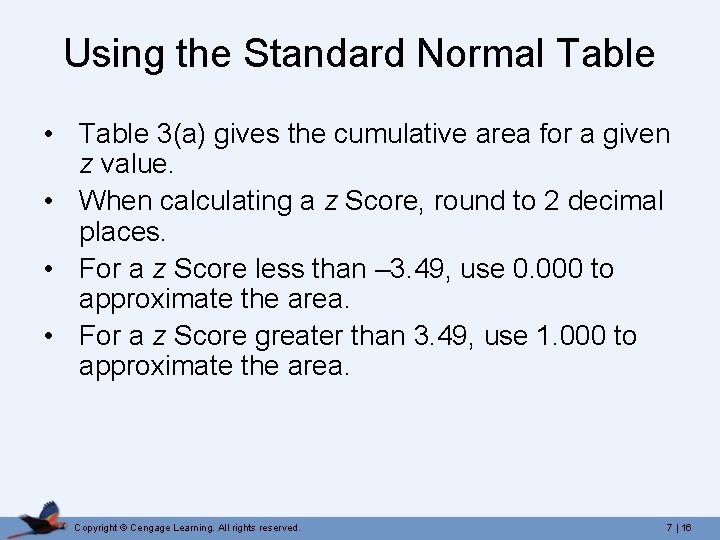
Using the Standard Normal Table • Table 3(a) gives the cumulative area for a given z value. • When calculating a z Score, round to 2 decimal places. • For a z Score less than – 3. 49, use 0. 000 to approximate the area. • For a z Score greater than 3. 49, use 1. 000 to approximate the area. Copyright © Cengage Learning. All rights reserved. 7 | 16
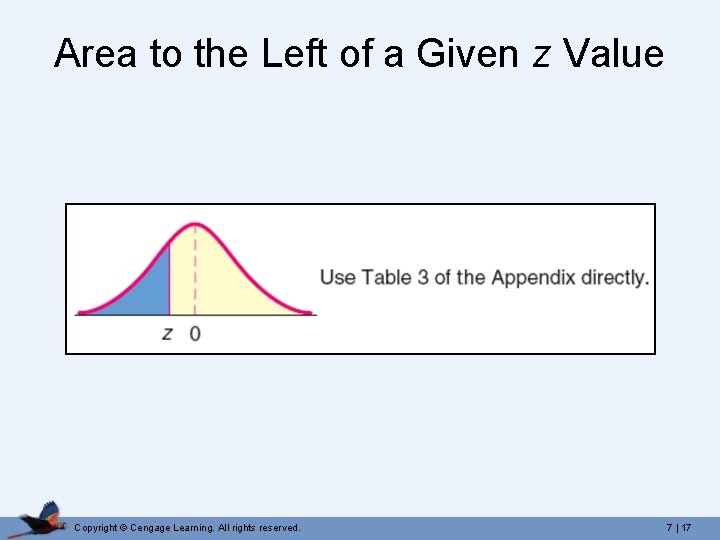
Area to the Left of a Given z Value Copyright © Cengage Learning. All rights reserved. 7 | 17
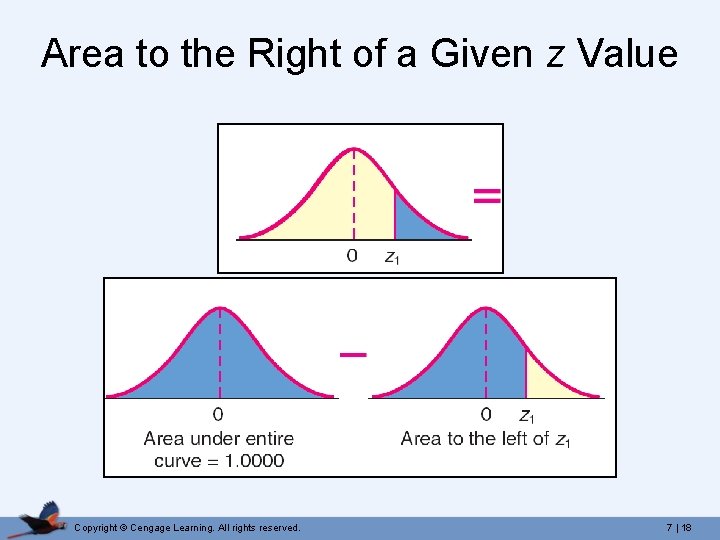
Area to the Right of a Given z Value Copyright © Cengage Learning. All rights reserved. 7 | 18
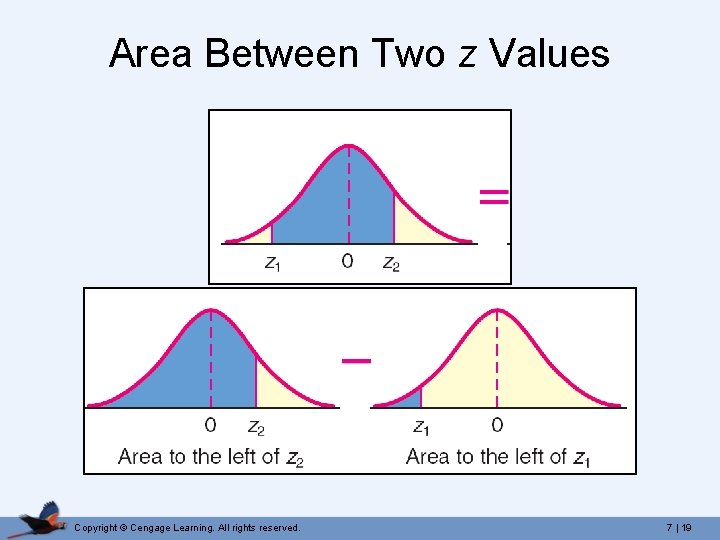
Area Between Two z Values Copyright © Cengage Learning. All rights reserved. 7 | 19
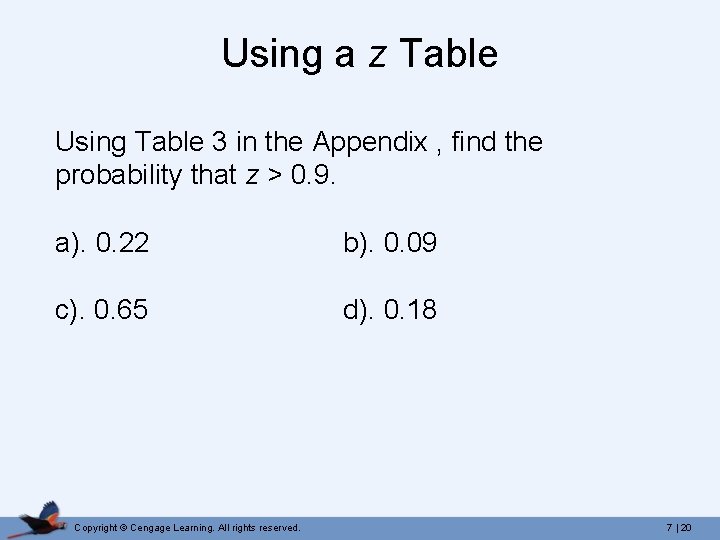
Using a z Table Using Table 3 in the Appendix , find the probability that z > 0. 9. a). 0. 22 b). 0. 09 c). 0. 65 d). 0. 18 Copyright © Cengage Learning. All rights reserved. 7 | 20
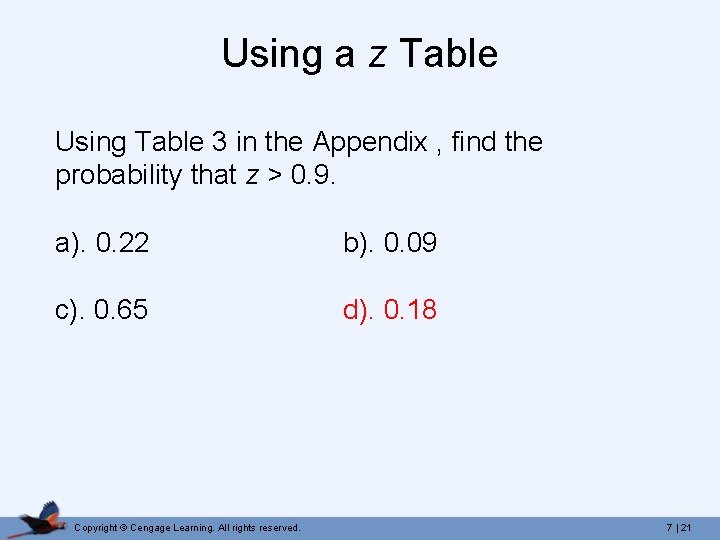
Using a z Table Using Table 3 in the Appendix , find the probability that z > 0. 9. a). 0. 22 b). 0. 09 c). 0. 65 d). 0. 18 Copyright © Cengage Learning. All rights reserved. 7 | 21

Normal Probability Final Remarks • The probability that z equals a certain number is always 0. – P(z = a) = 0 • Therefore, < and ≤ can be used interchangeably. Similarly, > and ≥ can be used interchangeably. – P(z < b) = P(z ≤ b) – P(z > c) = P(z ≥ c) Copyright © Cengage Learning. All rights reserved. 7 | 22

Inverse Normal Distribution • Sometimes we need to find an x or z that corresponds to a given area under the normal curve. – In Table 3, we look up an area and find the corresponding z. Copyright © Cengage Learning. All rights reserved. 7 | 23

Finding z Corresponding to a Given Area A (0 < A < 1) Left-tail case: the given area is to the left of z. Look up the number A in the body of the table and use the corresponding z value. Copyright © Cengage Learning. All rights reserved. 7 | 24
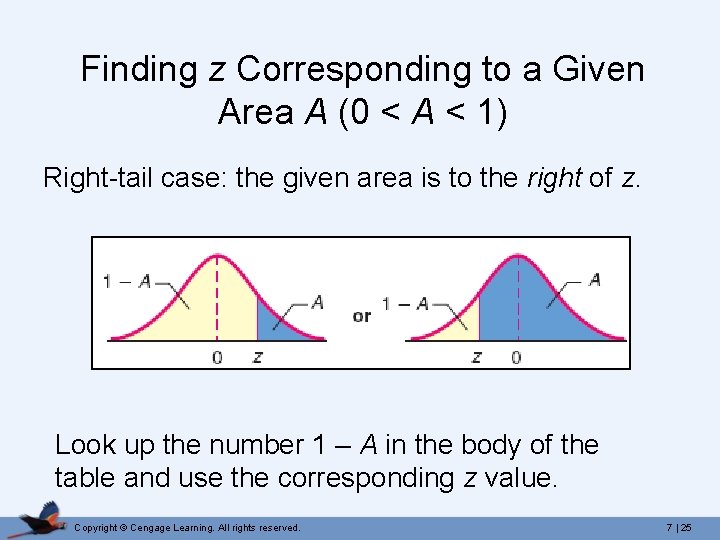
Finding z Corresponding to a Given Area A (0 < A < 1) Right-tail case: the given area is to the right of z. Look up the number 1 – A in the body of the table and use the corresponding z value. Copyright © Cengage Learning. All rights reserved. 7 | 25

Finding z Corresponding to a Given Area A (0 < A < 1) Center-tail case: the given area is symmetric and centered above z = 0. Look up the number (1 – A)/2 in the body of the table and use the corresponding ±z value. Copyright © Cengage Learning. All rights reserved. 7 | 26

Inverse Normal Distribution Using Table 3 in the Appendix, find the range of z scores, centered about the mean, that contain 70% of the probability. a). – 1. 04 to 1. 04 b). – 2. 17 to 2. 17 c). – 0. 30 to 0. 30 d). – 0. 52 to 0. 52 Copyright © Cengage Learning. All rights reserved. 7 | 27

Inverse Normal Distribution Using Table 3 in the Appendix, find the range of z scores, centered about the mean, that contain 70% of the probability. a). – 1. 04 to 1. 04 b). – 2. 17 to 2. 17 c). – 0. 30 to 0. 30 d). – 0. 52 to 0. 52 Copyright © Cengage Learning. All rights reserved. 7 | 28

Critical Thinking – How to tell if data follow a normal distribution? • Histogram – a normal distribution’s histogram should be roughly bell-shaped. • Outliers – a normal distribution should have no more than one outlier Copyright © Cengage Learning. All rights reserved. 7 | 29

Critical Thinking – How to tell if data follow a normal distribution? • Skewness –normal distributions are symmetric. Use the Pearson’s index: Pearson’s index = A Pearson’s index greater than 1 or less than – 1 indicates skewness. • Normal quantile plot – using a statistical software (see the Using Technology feature. ) Copyright © Cengage Learning. All rights reserved. 7 | 30

Terms, Statistics & Parameters • Terms: Population, Sample, Parameter, Statistics Copyright © Cengage Learning. All rights reserved. 7 | 31

Why Sample? • If time and resources are limited, we take samples to learn about the population. Copyright © Cengage Learning. All rights reserved. 7 | 32

Types of Inference 1) Estimation: We estimate the value of a population parameter. 2) Testing: We formulate a decision about a population parameter. 3) Regression: We make predictions about the value of a statistical variable. Copyright © Cengage Learning. All rights reserved. 7 | 33

Sampling Distributions • To evaluate the reliability of our inference, we need to know about the probability distribution of the statistic we are using. • Typically, we are interested in the sampling distributions for sample means and sample proportions. Copyright © Cengage Learning. All rights reserved. 7 | 34

The Central Limit Theorem (Normal) • If x is a random variable with a normal distribution, mean = µ, and standard deviation = σ, then the following holds for any sample size: (n is the sample size) Copyright © Cengage Learning. All rights reserved. 7 | 35

The Standard Error • The standard error is just another name for the standard deviation of the sampling distribution. Copyright © Cengage Learning. All rights reserved. 7 | 36

The Central Limit Theorem (Any Distribution) • If a random variable has any distribution with mean = µ and standard deviation = σ, the sampling distribution of will approach a normal distribution with mean = µ and standard deviation = as n increases without limit. Copyright © Cengage Learning. All rights reserved. 7 | 37

Sample Size Considerations • For the Central Limit Theorem (CLT) to be applicable: – If the x distribution is symmetric or reasonably symmetric, n ≥ 30 should suffice. – If the x distribution is highly skewed or unusual, even larger sample sizes will be required. – If possible, make a graph to visualize how the sampling distribution is behaving. Copyright © Cengage Learning. All rights reserved. 7 | 38

Critical Thinking • Bias – A sample statistic is unbiased if the mean of its sampling distribution equals the value of the parameter being estimated. • Variability – The spread of the sampling distribution indicates the variability of the statistic. Copyright © Cengage Learning. All rights reserved. 7 | 39

Normal Approximation to the Binomial Copyright © Cengage Learning. All rights reserved. 7 | 40

Normal Approximation to the Binomial A fair coin is flipped 200 times and the number of heads, x, is counted. Find the normal approximation of the standard deviation for this experiment. a). 50 b). 7. 07 Copyright © Cengage Learning. All rights reserved. c). 10 d). 100 7 | 41

Normal Approximation to the Binomial A fair coin is flipped 200 times and the number of heads, x, is counted. Find the normal approximation of the standard deviation for this experiment. a). 50 b). 7. 07 Copyright © Cengage Learning. All rights reserved. c). 10 d). 100 7 | 42

Continuity Correction Copyright © Cengage Learning. All rights reserved. 7 | 43
- Slides: 43