CS 3343 Analysis of Algorithms Lecture 21 Introduction













- Slides: 56

CS 3343: Analysis of Algorithms Lecture 21: Introduction to Graphs

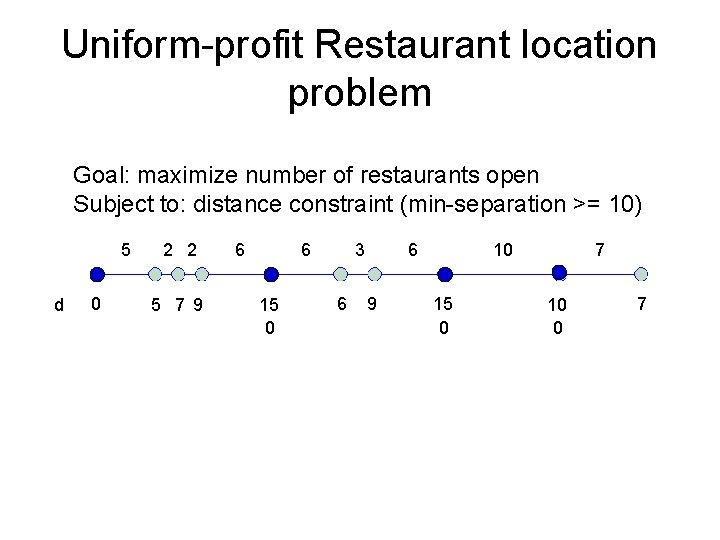
Uniform-profit Restaurant location problem Goal: maximize number of restaurants open Subject to: distance constraint (min-separation >= 10) 5 d 0 2 2 5 7 9 6 6 15 0 3 6 6 9 10 15 0 7 10 0 7

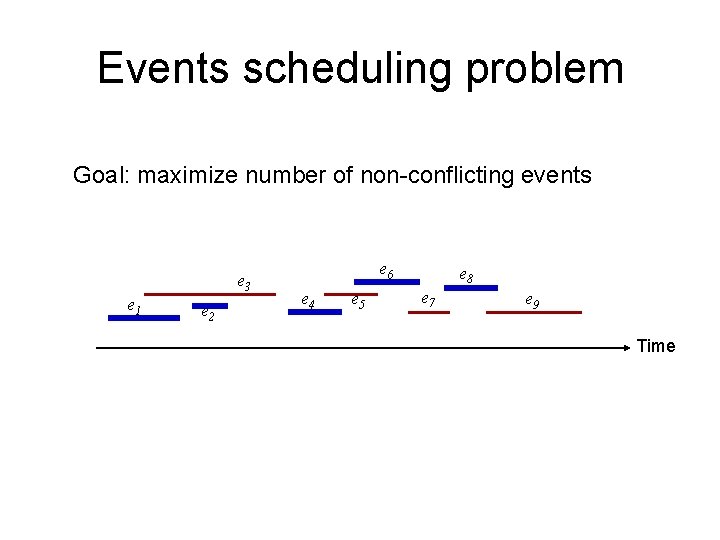
Events scheduling problem Goal: maximize number of non-conflicting events e 3 e 1 e 2 e 6 e 4 e 5 e 8 e 7 e 9 Time

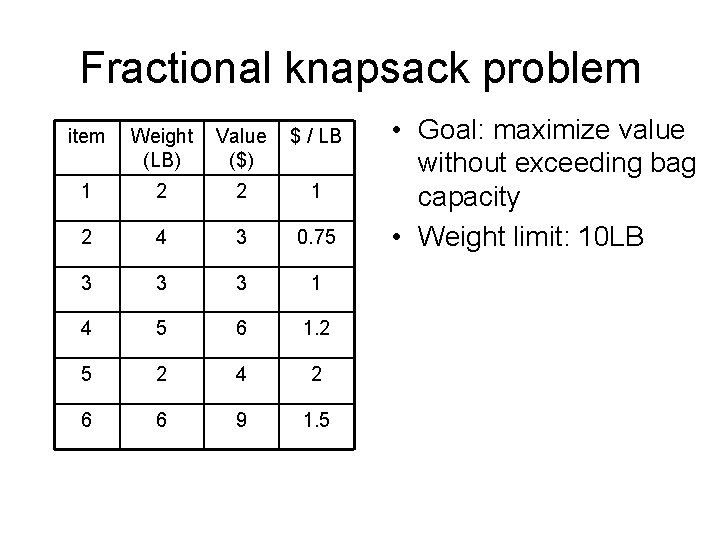
Fractional knapsack problem item Weight (LB) Value ($) $ / LB 1 2 2 1 2 4 3 0. 75 3 3 3 1 4 5 6 1. 2 5 2 4 2 6 6 9 1. 5 • Goal: maximize value without exceeding bag capacity • Weight limit: 10 LB

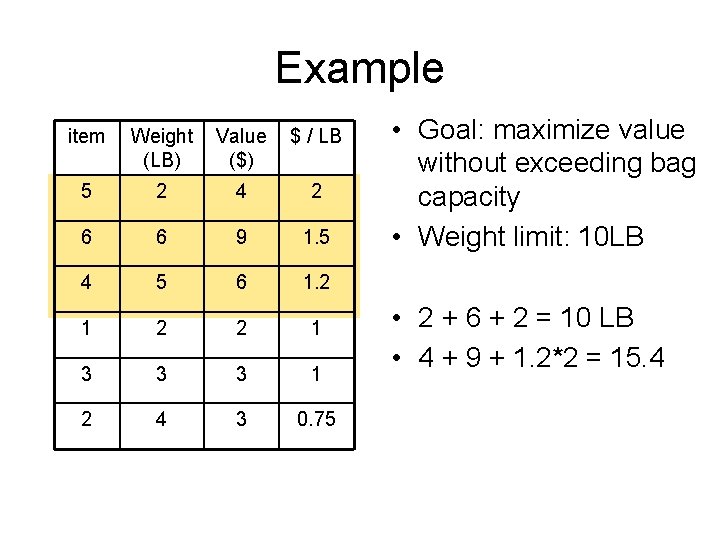
Example item Weight (LB) Value ($) $ / LB 5 2 4 2 6 6 9 1. 5 4 5 6 1. 2 1 2 2 1 3 3 3 1 2 4 3 0. 75 • Goal: maximize value without exceeding bag capacity • Weight limit: 10 LB • 2 + 6 + 2 = 10 LB • 4 + 9 + 1. 2*2 = 15. 4

The remaining lectures • Graph algorithms • Very important in practice – Tons of computational problems can be defined in terms of graphs – We’ll study a few interesting ones • • Minimum spanning tree Shortest path Graph search Topological sort, connected components

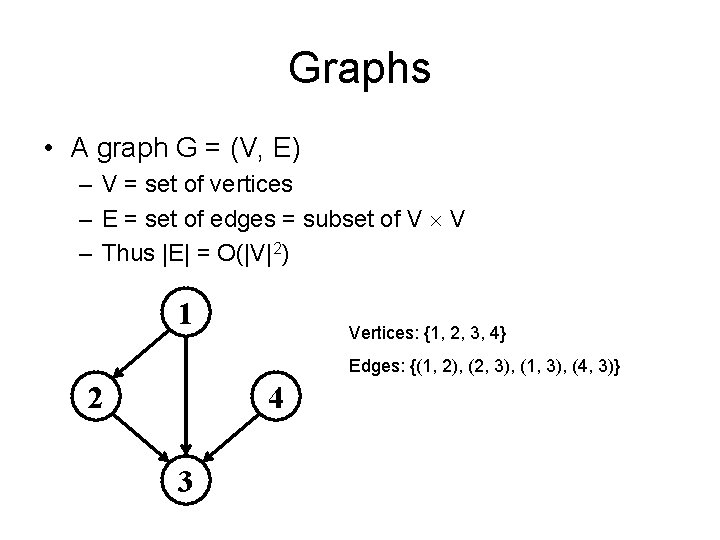
Graphs • A graph G = (V, E) – V = set of vertices – E = set of edges = subset of V V – Thus |E| = O(|V|2) 1 Vertices: {1, 2, 3, 4} Edges: {(1, 2), (2, 3), (1, 3), (4, 3)} 2 4 3

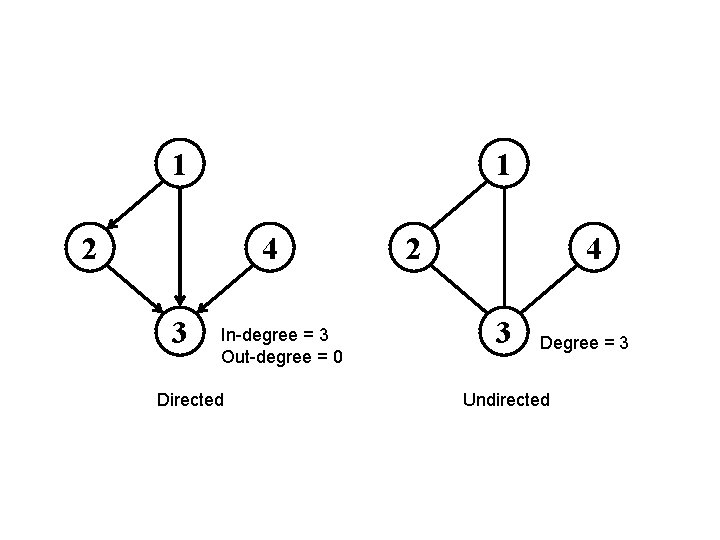
Graph Variations (1) • Directed / undirected: – In an undirected graph: • Edge (u, v) E implies edge (v, u) E • Road networks between cities – In a directed graph: • Edge (u, v): u v does not imply v u • Street networks in downtown – Degree of vertex v: • The number of edges adjacency to v • For directed graph, there are in-degree and out-degree

1 1 2 4 3 In-degree = 3 Out-degree = 0 Directed 2 4 3 Degree = 3 Undirected

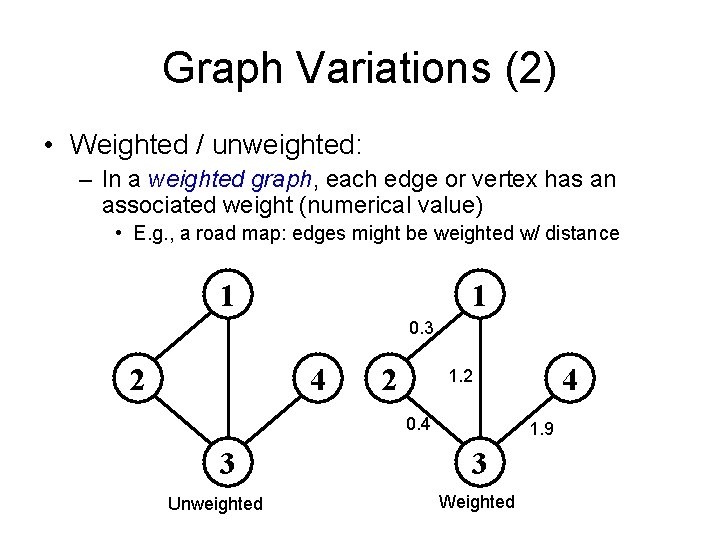
Graph Variations (2) • Weighted / unweighted: – In a weighted graph, each edge or vertex has an associated weight (numerical value) • E. g. , a road map: edges might be weighted w/ distance 1 1 0. 3 2 4 2 0. 4 3 Unweighted 4 1. 2 1. 9 3 Weighted

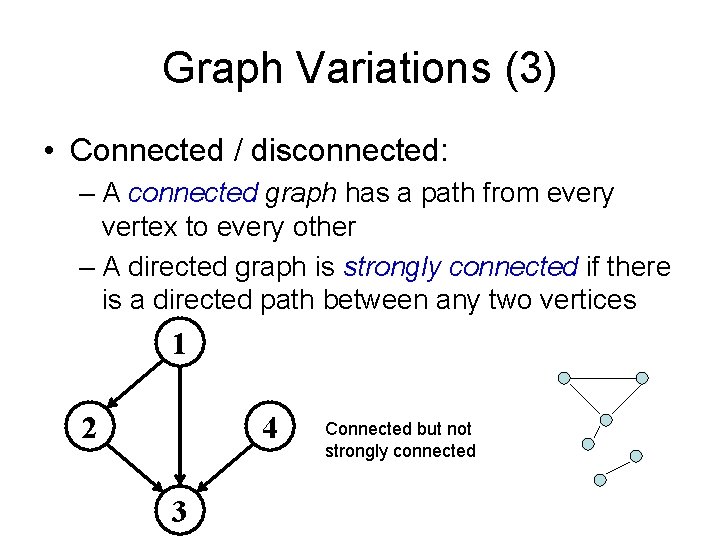
Graph Variations (3) • Connected / disconnected: – A connected graph has a path from every vertex to every other – A directed graph is strongly connected if there is a directed path between any two vertices 1 2 4 3 Connected but not strongly connected

Graph Variations (4) • Dense / sparse: – Graphs are sparse when the number of edges is linear to the number of vertices • |E| O(|V|) – Graphs are dense when the number of edges is quadratic to the number of vertices • |E| O(|V|2) – Most graphs of interest are sparse – If you know you are dealing with dense or sparse graphs, different data structures may make sense

Representing Graphs • Assume V = {1, 2, …, n} • An adjacency matrix represents the graph as a n x n matrix A: – A[i, j] = 1 if edge (i, j) E = 0 if edge (i, j) E • For weighted graph – A[i, j] = wij if edge (i, j) E = 0 if edge (i, j) E • For undirected graph – Matrix is symmetric: A[i, j] = A[j, i]

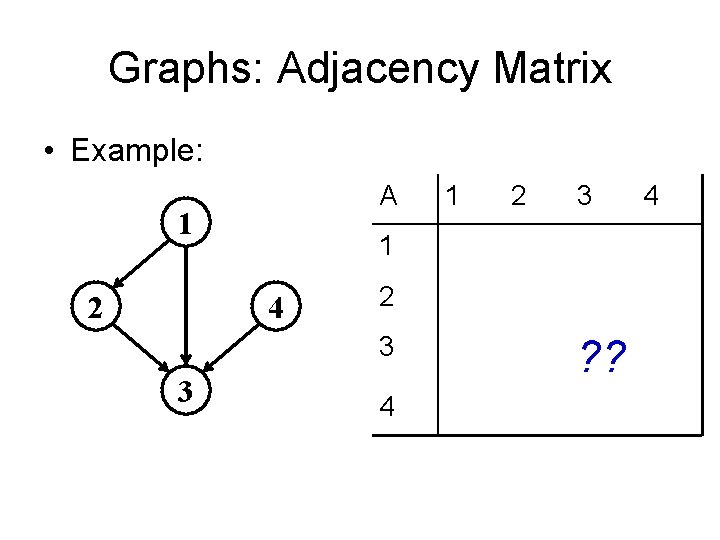
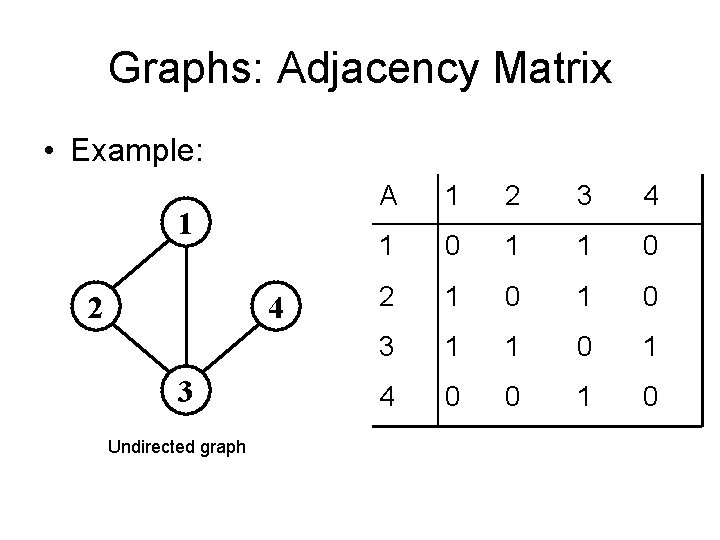
Graphs: Adjacency Matrix • Example: A 1 2 2 3 1 4 2 3 3 1 4 ? ? 4

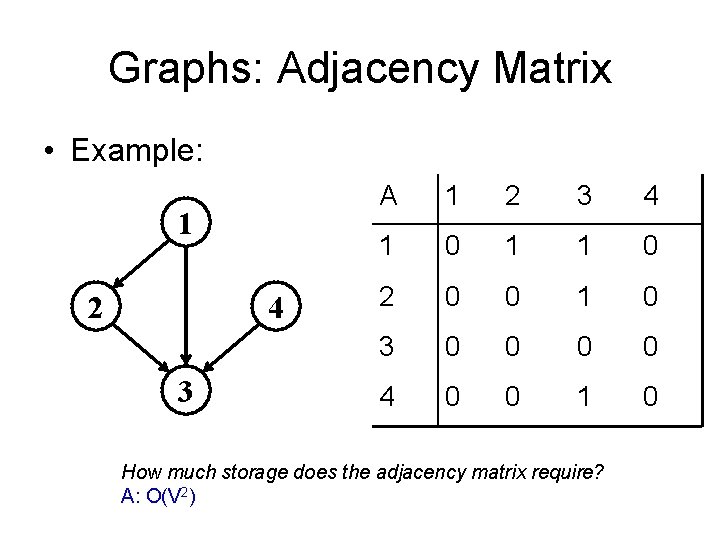
Graphs: Adjacency Matrix • Example: 1 2 4 3 A 1 2 3 4 1 0 1 1 0 2 0 0 1 0 3 0 0 4 0 0 1 0 How much storage does the adjacency matrix require? A: O(V 2)

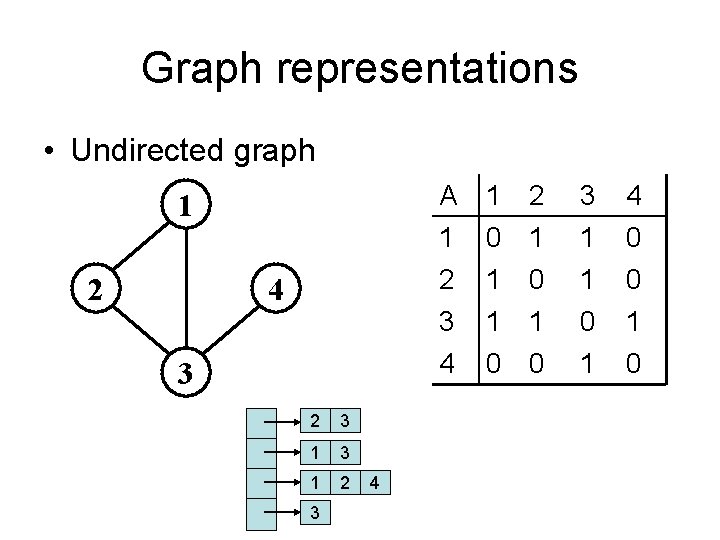
Graphs: Adjacency Matrix • Example: 1 2 4 3 Undirected graph A 1 2 3 4 1 0 1 1 0 2 1 0 3 1 1 0 1 4 0 0 1 0

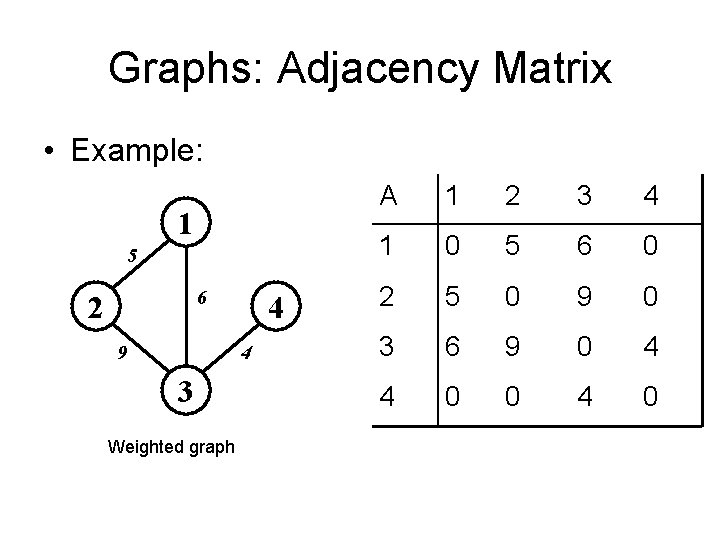
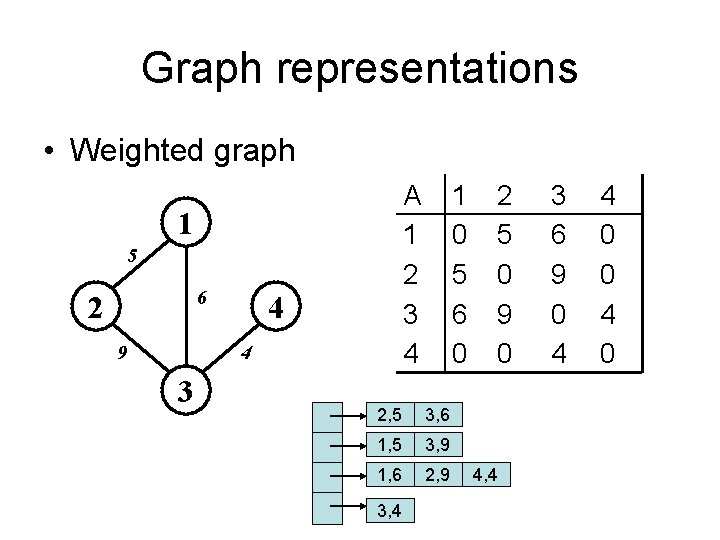
Graphs: Adjacency Matrix • Example: 1 5 6 2 9 4 4 3 Weighted graph A 1 2 3 4 1 0 5 6 0 2 5 0 9 0 3 6 9 0 4 4 0 0 4 0

Graphs: Adjacency Matrix • Time to answer if there is an edge between vertex u and v: Θ(1) • Memory required: Θ(n 2) regardless of |E| – Usually too much storage for large graphs – But can be very efficient for small graphs • Most large interesting graphs are sparse – E. g. , road networks (due to limit on junctions) – For this reason the adjacency list is often a more appropriate representation

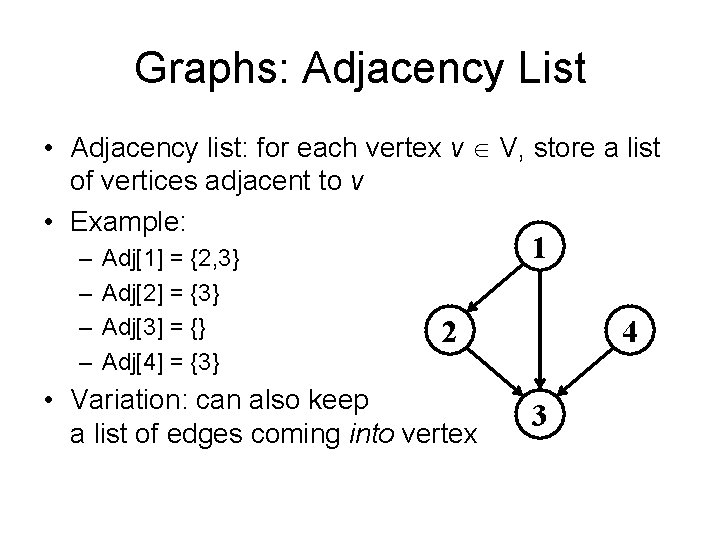
Graphs: Adjacency List • Adjacency list: for each vertex v V, store a list of vertices adjacent to v • Example: – – Adj[1] = {2, 3} Adj[2] = {3} Adj[3] = {} Adj[4] = {3} 1 2 • Variation: can also keep a list of edges coming into vertex 4 3

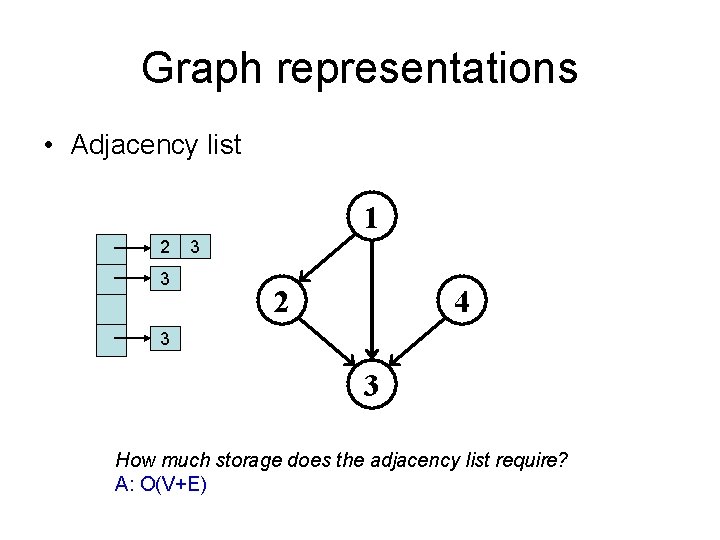
Graph representations • Adjacency list 1 2 3 3 2 4 3 3 How much storage does the adjacency list require? A: O(V+E)

Graph representations • Undirected graph 1 2 4 3 2 3 1 2 3 4 A 1 2 0 1 1 0 3 1 1 4 0 0 3 4 1 1 0 0 0 1 1 0

Graph representations • Weighted graph A 1 2 3 4 1 5 6 2 9 4 4 3 1 0 5 6 0 2, 5 3, 6 1, 5 3, 9 1, 6 2, 9 3, 4 2 5 0 9 0 4, 4 3 6 9 0 4 4 0 0 4 0

Graphs: Adjacency List • How much storage is required? • For directed graphs – |adj[v]| = out-degree(v) – Total # of items in adjacency lists is out-degree(v) = |E| • For undirected graphs – |adj[v]| = degree(v) – # items in adjacency lists is degree(v) = 2 |E| • So: Adjacency lists take (V+E) storage • Time needed to test if edge (u, v) E is O(n)

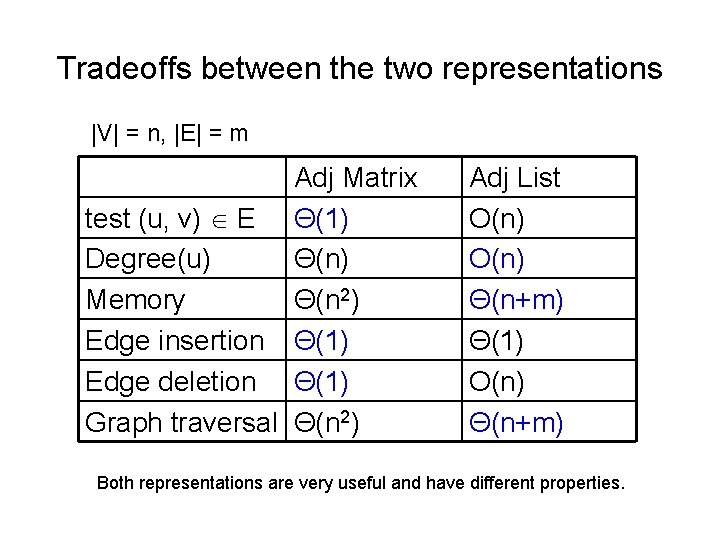
Tradeoffs between the two representations |V| = n, |E| = m Adj Matrix test (u, v) E Θ(1) Degree(u) Θ(n) Memory Θ(n 2) Edge insertion Θ(1) Edge deletion Θ(1) Graph traversal Θ(n 2) Adj List O(n) Θ(n+m) Θ(1) O(n) Θ(n+m) Both representations are very useful and have different properties.

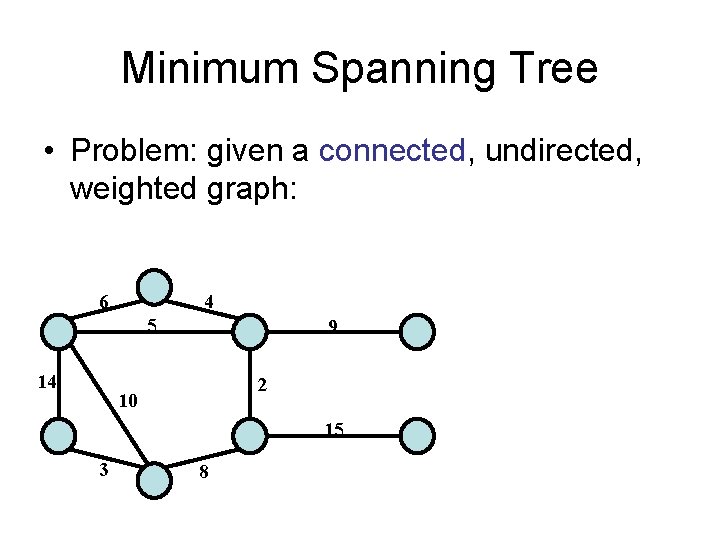
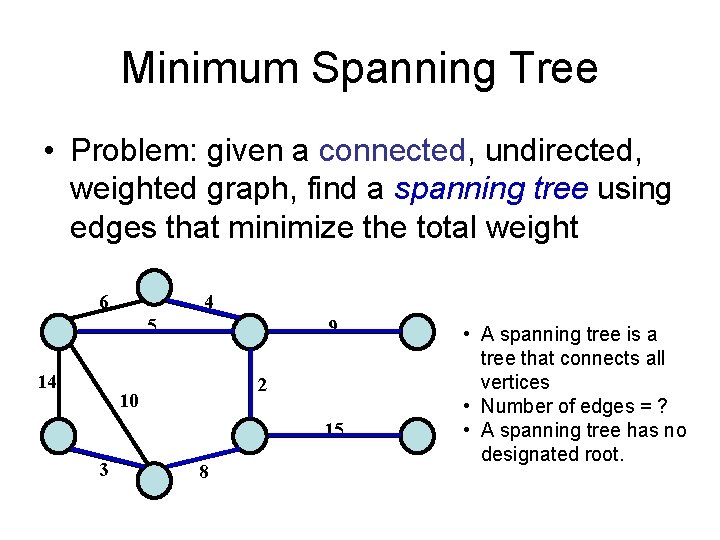
Minimum Spanning Tree • Problem: given a connected, undirected, weighted graph: 6 4 5 14 9 2 10 15 3 8

Minimum Spanning Tree • Problem: given a connected, undirected, weighted graph, find a spanning tree using edges that minimize the total weight 6 4 5 14 9 2 10 15 3 8 • A spanning tree is a tree that connects all vertices • Number of edges = ? • A spanning tree has no designated root.

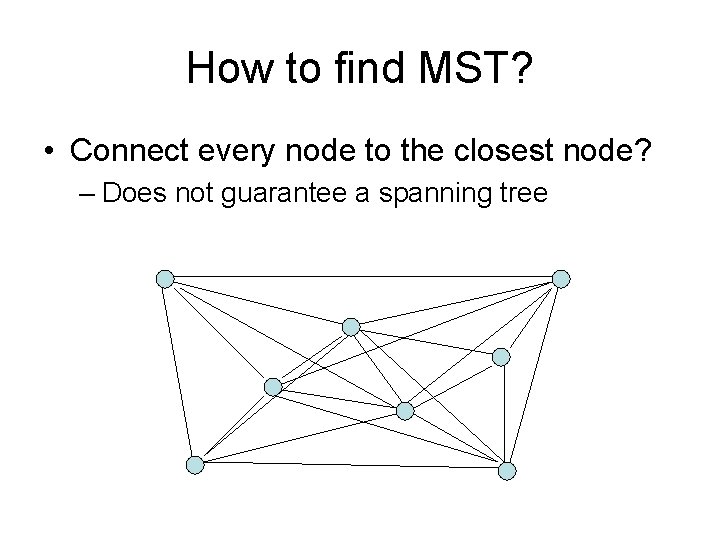
How to find MST? • Connect every node to the closest node? – Does not guarantee a spanning tree

Minimum Spanning Tree • MSTs satisfy the optimal substructure property: an optimal tree is composed of optimal subtrees – Let T be an MST of G with an edge (u, v) in the middle – Removing (u, v) partitions T into two trees T 1 and T 2 – w(T) = w(u, v) + w(T 1) + w(T 2) • Claim 1: T 1 is an MST of G 1 = (V 1, E 1), and T 2 is an MST of G 2 = (V 2, E 2) T 2 T 1 ’ u v Proof by contradiction: • if T 1 is not optimal, we can replace T 1 with a better spanning tree, T 1’ • T 1’, T 2 and (u, v) form a new spanning tree T’ • W(T’) < W(T). Contradiction.

Minimum Spanning Tree • MSTs satisfy the optimal substructure property: an optimal tree is composed of optimal subtrees – Let T be an MST of G with an edge (u, v) in the middle – Removing (u, v) partitions T into two trees T 1 and T 2 – w(T) = w(u, v) + w(T 1) + w(T 2) • Claim 2: (u, v) is the lightest edge connecting G 1 = (V 1, E 1) and G 2 = (V 2, E 2) T 2 T 1 x u v y Proof by contradiction: • if (u, v) is not the lightest edge, we can remove it, and reconnect T 1 and T 2 with a lighter edge (x, y) • T 1, T 2 and (x, y) form a new spanning tree T’ • W(T’) < W(T). Contradiction.

Algorithms • Generic idea: – Compute MSTs for sub-graphs – Connect two MSTs for sub-graphs with the lightest edge • Two of the most well-known algorithms – Prim’s algorithm – Kruskal’s algorithm – Let’s first talk about the ideas behind the algorithms without worrying about the implementation and analysis

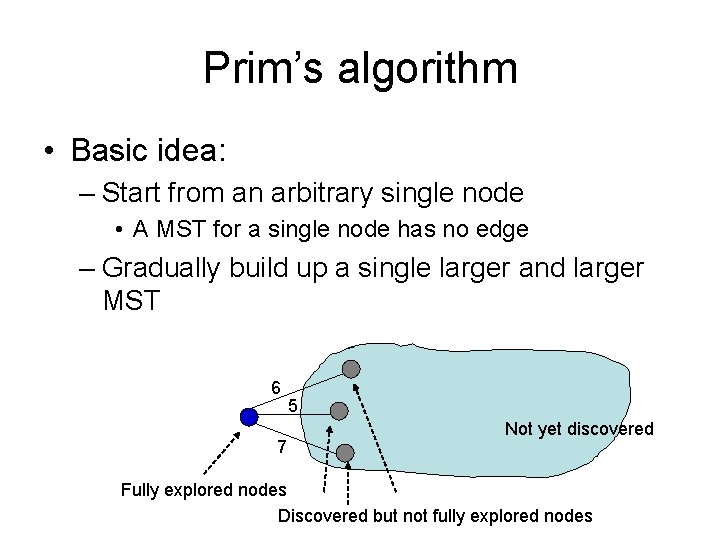
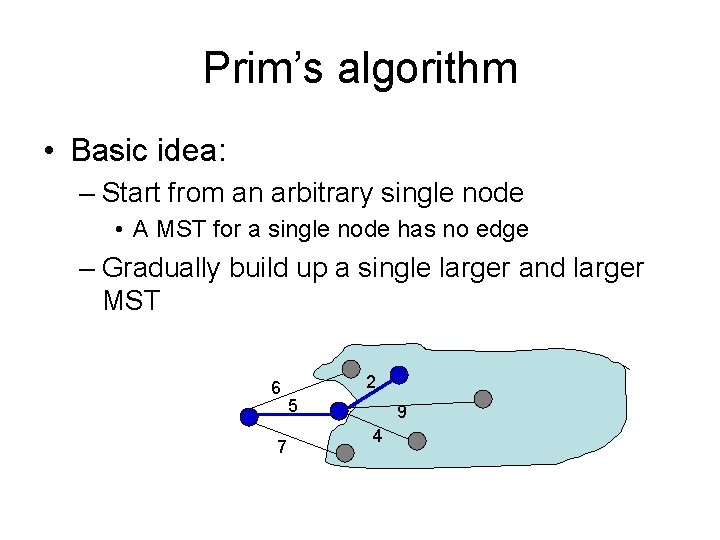
Prim’s algorithm • Basic idea: – Start from an arbitrary single node • A MST for a single node has no edge – Gradually build up a single larger and larger MST 6 7 5 Not yet discovered Fully explored nodes Discovered but not fully explored nodes

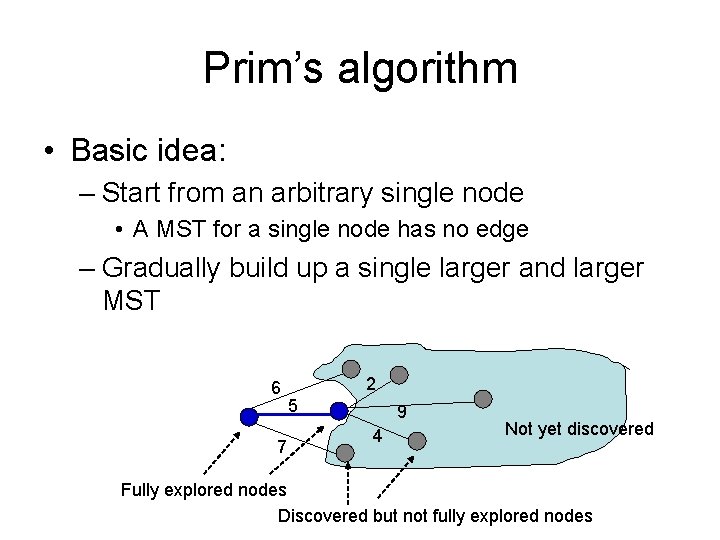
Prim’s algorithm • Basic idea: – Start from an arbitrary single node • A MST for a single node has no edge – Gradually build up a single larger and larger MST 6 7 2 5 9 4 Not yet discovered Fully explored nodes Discovered but not fully explored nodes

Prim’s algorithm • Basic idea: – Start from an arbitrary single node • A MST for a single node has no edge – Gradually build up a single larger and larger MST 6 7 2 5 9 4

Prim’s algorithm in words • Randomly pick a vertex as the initial tree T • Gradually expand into a MST: – For each vertex that is not in T but directly connected to some nodes in T • Compute its minimum distance to any vertex in T – Select the vertex that is closest to T • Add it to T

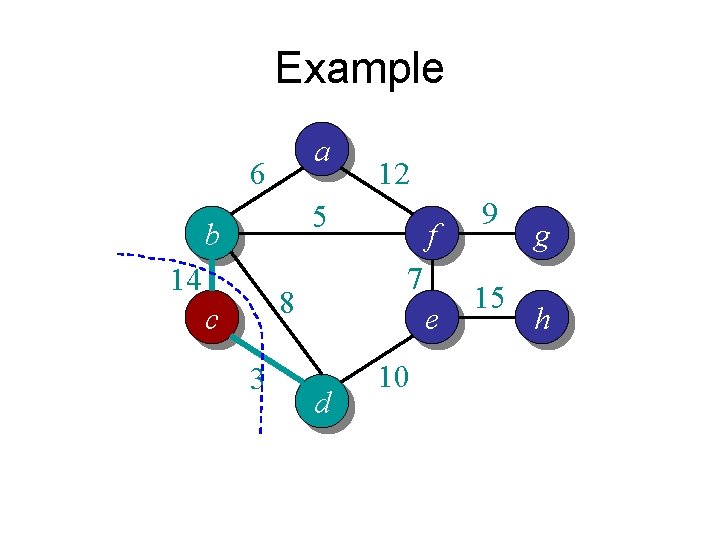
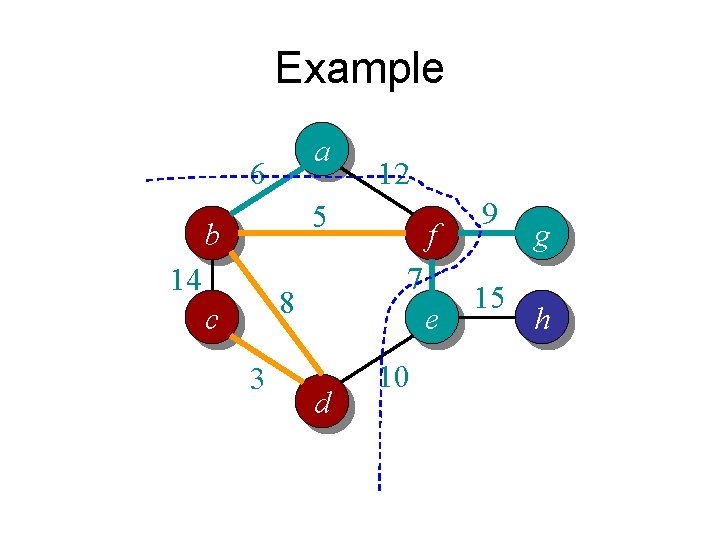
Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

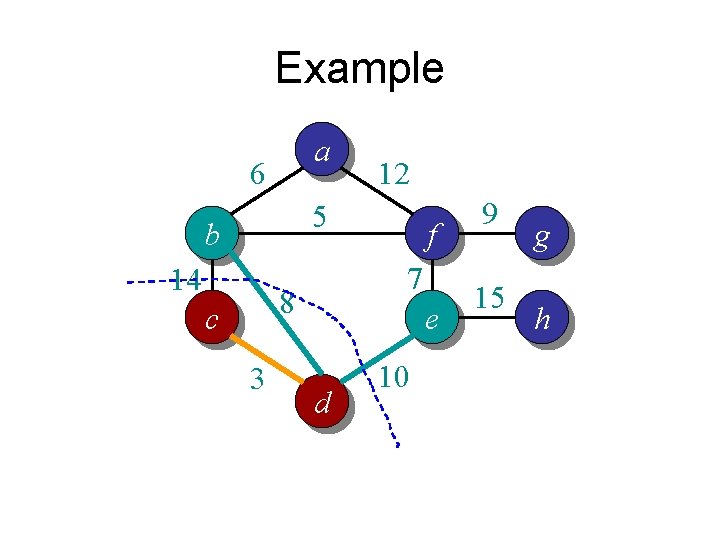
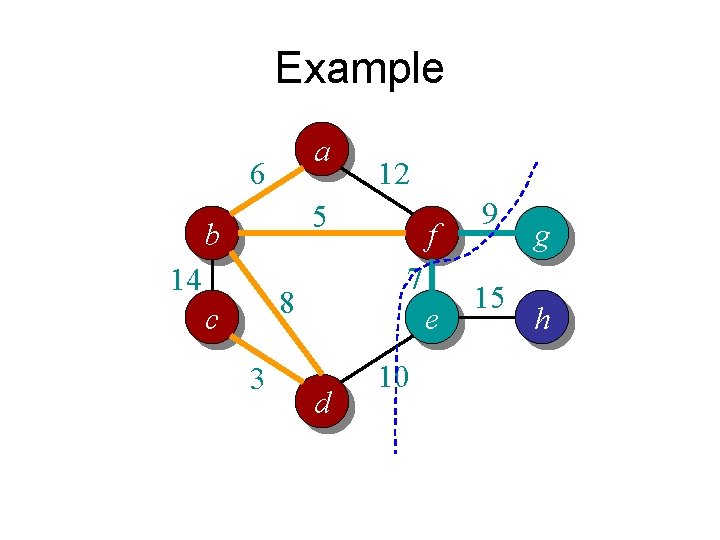
Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

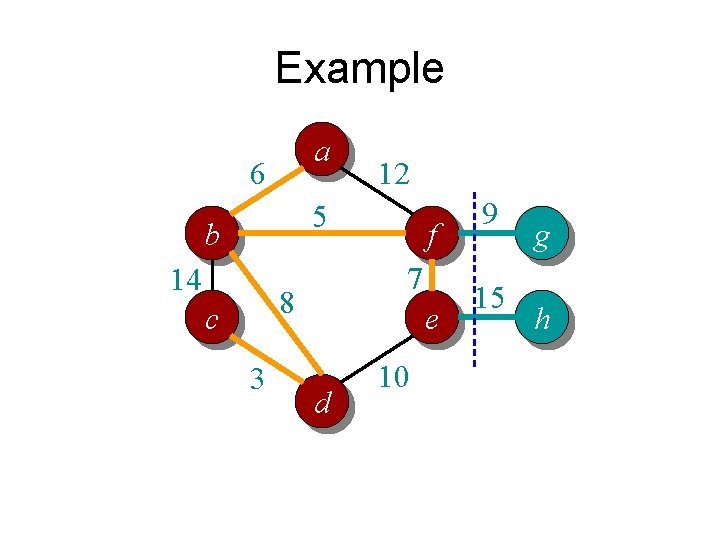
Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

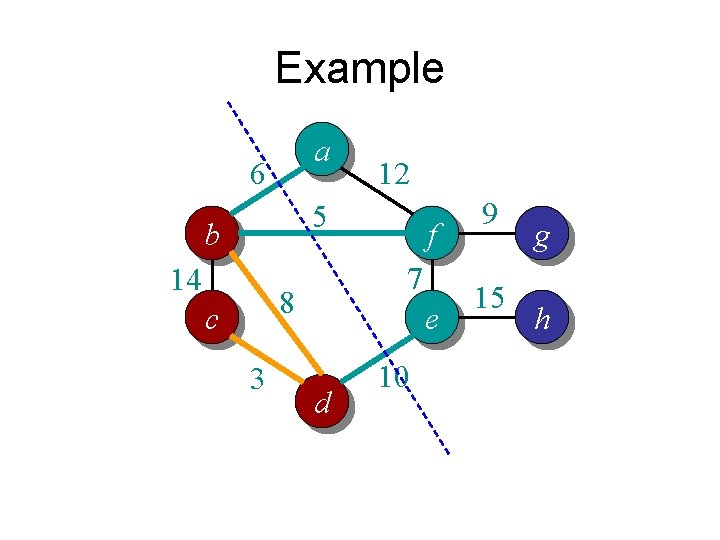
Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

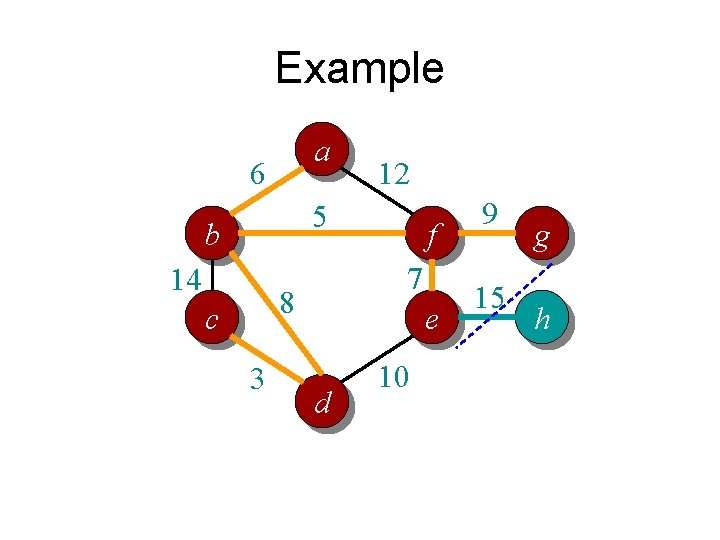
Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

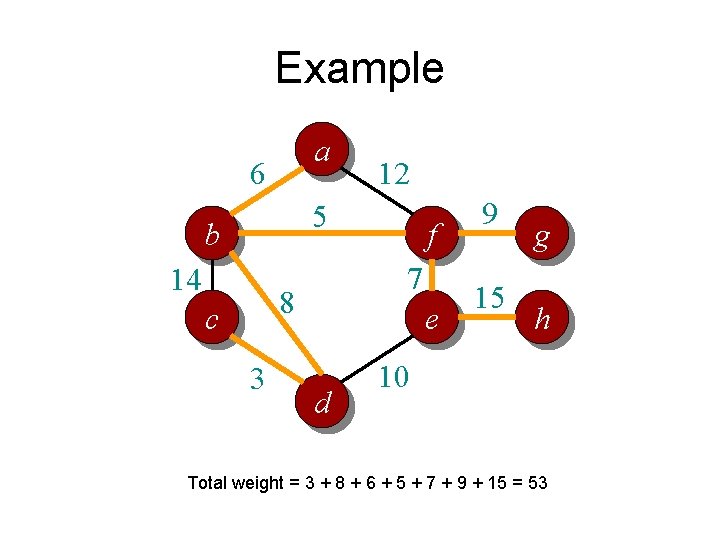
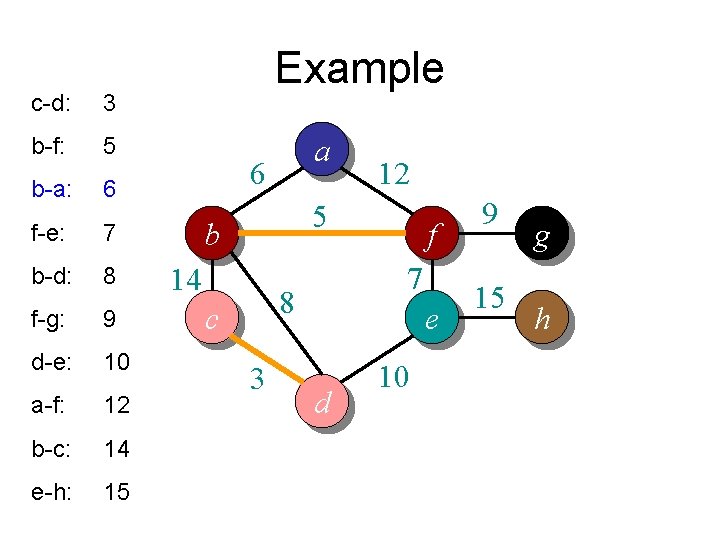
Example a 6 12 5 b 14 7 8 c 3 f e d 9 15 g h 10 Total weight = 3 + 8 + 6 + 5 + 7 + 9 + 15 = 53

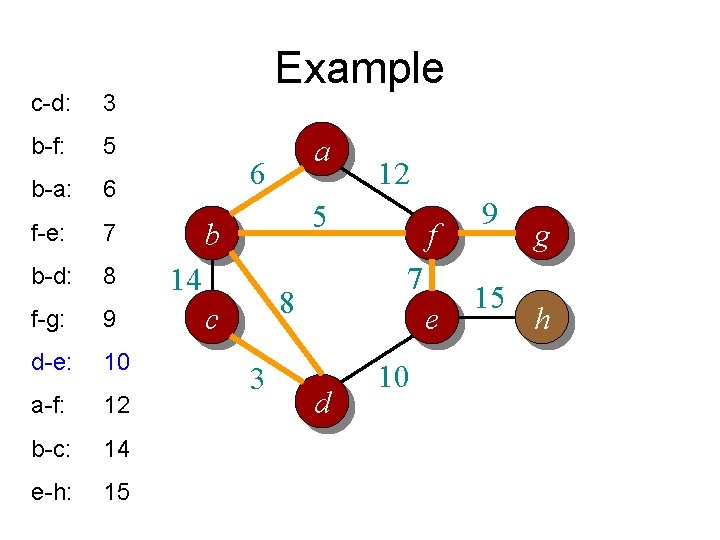
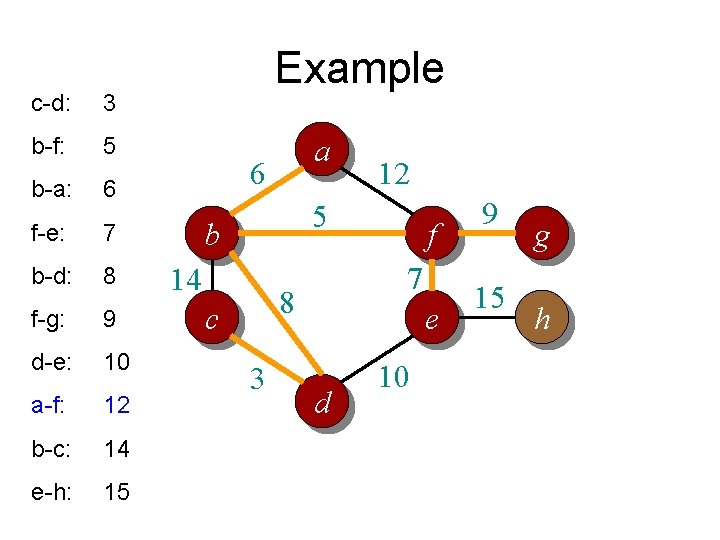
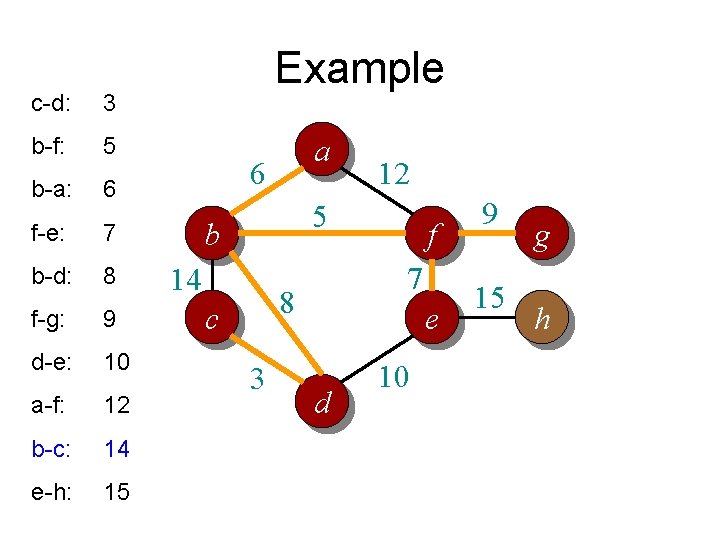
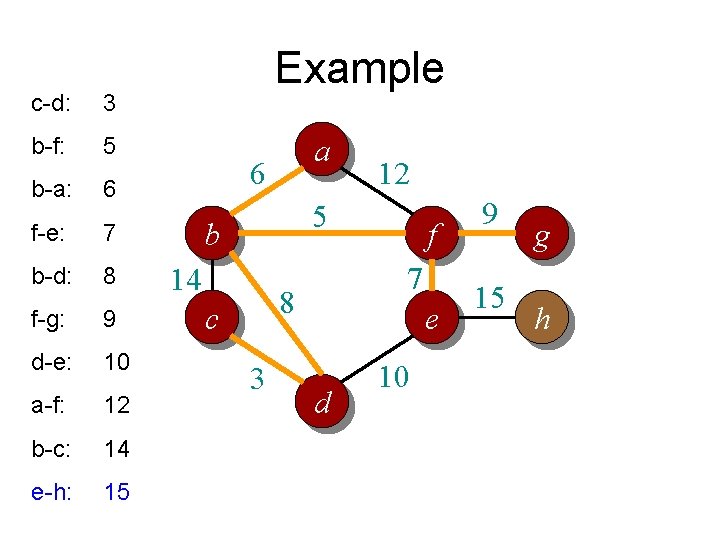
Kruskal’s algorithm • Basic idea: – Grow many small trees – Find two trees that are closest (i. e. , connected with the lightest edge), join them with the lightest edge – Terminate when a single tree forms

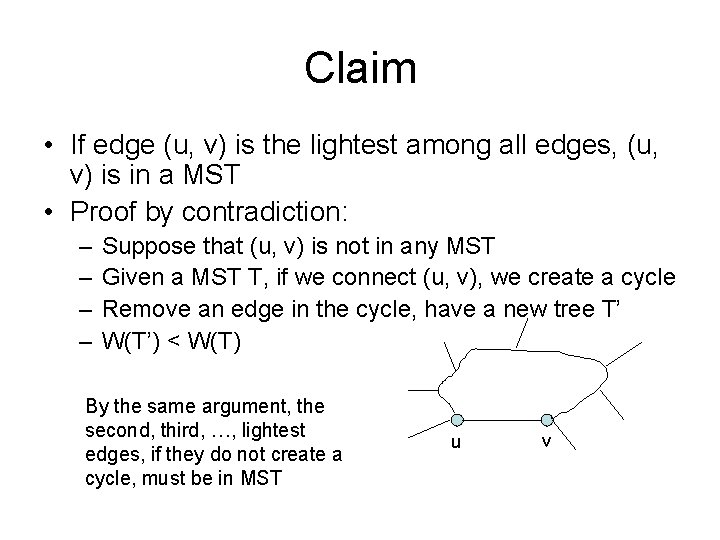
Claim • If edge (u, v) is the lightest among all edges, (u, v) is in a MST • Proof by contradiction: – – Suppose that (u, v) is not in any MST Given a MST T, if we connect (u, v), we create a cycle Remove an edge in the cycle, have a new tree T’ W(T’) < W(T) By the same argument, the second, third, …, lightest edges, if they do not create a cycle, must be in MST u v

Kruskal’s algorithm in words • Procedure: – Sort all edges into non-decreasing order – Initially each node is in its own tree – For each edge in the sorted list • If the edge connects two separate trees, then – join the two trees together with that edge

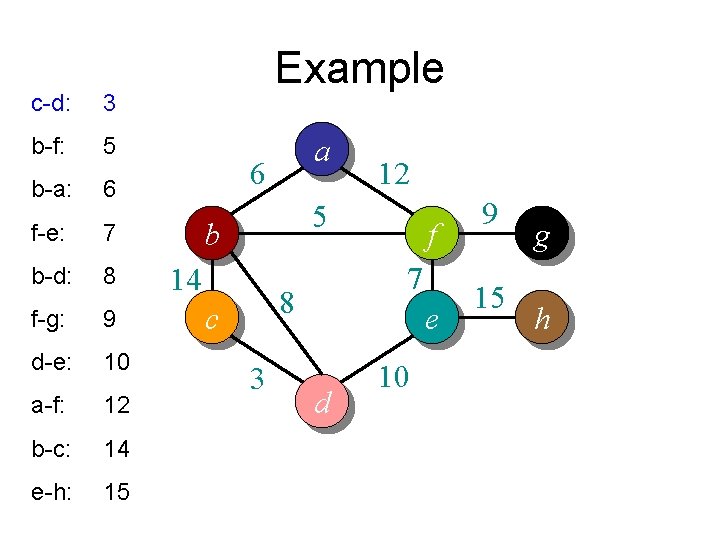
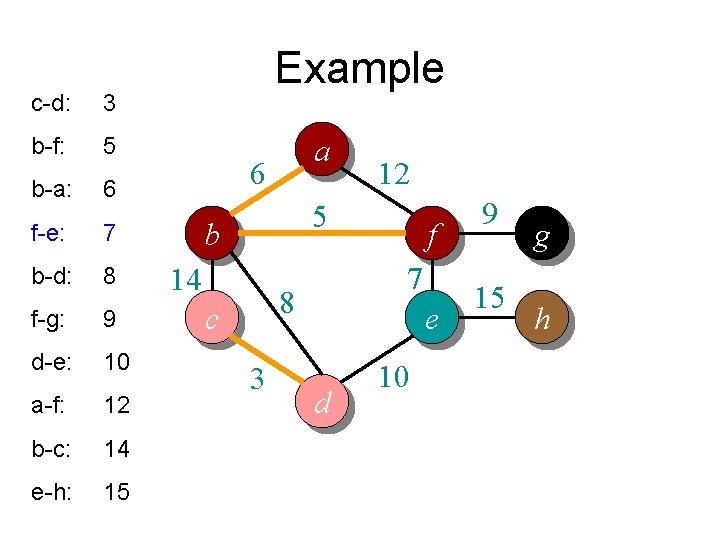
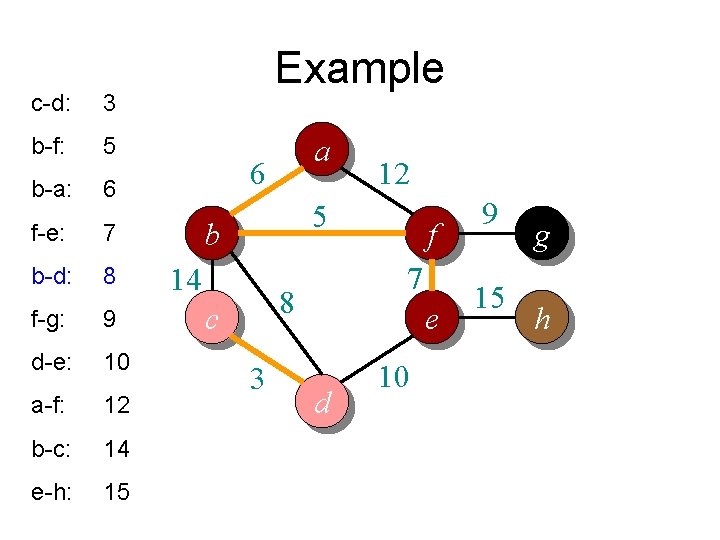
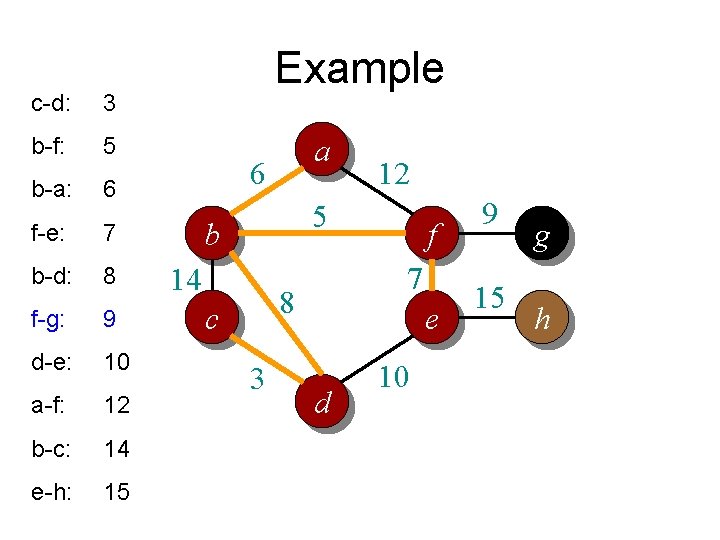
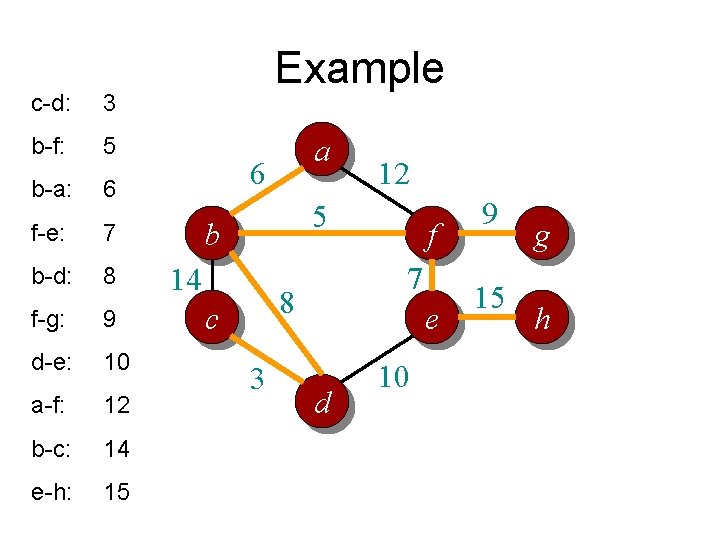
c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

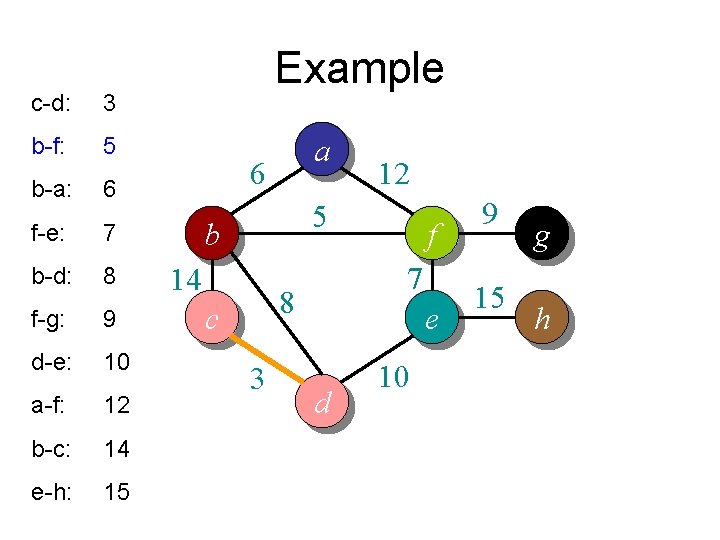
c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h

c-d: 3 b-f: 5 b-a: 6 f-e: 7 b-d: 8 f-g: 9 d-e: 10 a-f: 12 b-c: 14 e-h: 15 Example a 6 12 5 b 14 7 8 c 3 f e d 10 9 15 g h
 Introduction to algorithms lecture notes
Introduction to algorithms lecture notes Analysis of algorithms lecture notes
Analysis of algorithms lecture notes An introduction to the analysis of algorithms
An introduction to the analysis of algorithms Introduction of design and analysis of algorithms
Introduction of design and analysis of algorithms Introduction to the design and analysis of algorithms
Introduction to the design and analysis of algorithms 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad An introduction to bioinformatics algorithms
An introduction to bioinformatics algorithms Introduction to algorithms
Introduction to algorithms Introduction to algorithms slides
Introduction to algorithms slides Introduction to algorithms 2nd edition
Introduction to algorithms 2nd edition Hsinmu
Hsinmu Introduction to sorting algorithms
Introduction to sorting algorithms Introduction to algorithms 2nd edition
Introduction to algorithms 2nd edition Introduction to algorithms 2nd edition
Introduction to algorithms 2nd edition Introduction to bioinformatics algorithms
Introduction to bioinformatics algorithms Bioinformatics
Bioinformatics 1001 design
1001 design What is analysis of algorithm
What is analysis of algorithm Association analysis: basic concepts and algorithms
Association analysis: basic concepts and algorithms Algorithm input output
Algorithm input output Analysis of algorithms
Analysis of algorithms Algorithm analysis examples
Algorithm analysis examples Steps in mathematical analysis of non recursive algorithm
Steps in mathematical analysis of non recursive algorithm Cluster analysis: basic concepts and algorithms
Cluster analysis: basic concepts and algorithms Randomized algorithms and probabilistic analysis
Randomized algorithms and probabilistic analysis Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Cjih
Cjih Goals of analysis of algorithms
Goals of analysis of algorithms Exercise 24
Exercise 24 Binary search in design and analysis of algorithms
Binary search in design and analysis of algorithms Competitive analysis algorithms
Competitive analysis algorithms Design and analysis of algorithms
Design and analysis of algorithms Design and analysis of algorithms
Design and analysis of algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Comp 482
Comp 482 Introduction to biochemistry lecture notes
Introduction to biochemistry lecture notes Introduction to psychology lecture
Introduction to psychology lecture Exploratory data analysis lecture notes
Exploratory data analysis lecture notes Sensitivity analysis lecture notes
Sensitivity analysis lecture notes Factor analysis lecture notes
Factor analysis lecture notes Streak plate
Streak plate Zline 667-36
Zline 667-36 Computational thinking algorithms and programming
Computational thinking algorithms and programming Types of algorithm
Types of algorithm Simple recursive algorithms
Simple recursive algorithms Safe patient handling algorithms
Safe patient handling algorithms Recursive method
Recursive method Types of randomized algorithms
Types of randomized algorithms Process mining algorithms
Process mining algorithms Evolution of logistics ppt
Evolution of logistics ppt Nature-inspired learning algorithms
Nature-inspired learning algorithms Tabu search tsp
Tabu search tsp Making good encryption algorithms
Making good encryption algorithms Statistical algorithms
Statistical algorithms Ajit diwan
Ajit diwan Disadvantages of greedy algorithm
Disadvantages of greedy algorithm N/a greedy
N/a greedy