CS 3343 Analysis of Algorithms Lecture 5 Solving

CS 3343: Analysis of Algorithms Lecture 5: Solving recurrence by recursion-tree method 11/29/2020 1

Problem of the day • How many multiplications do you need to compute 316? 316 =3 x 3 …. x 3 Answer: 15 316 =38 x 38 38 =34 x 34 34 =32 x 32 Answer: 4 32 =3 x 3 11/29/2020 2

Pseudo code int pow (b, n) // compute bn m = n >> 1; p = pow (b, m); p = p * p; if (n % 2) return p * b; else return p; 11/29/2020 3

Pseudo code int pow (b, n) m = n >> 1; p = pow (b, m); p = p * p; if (n % 2) return p * b; else return p; 11/29/2020 int pow (b, n) m = n >> 1; p = pow(b, m) * pow(b, m); if (n % 2) return p * b; else return p; 4

Outline • Review of last lecture – analyzing recursive algorithms – Defining recurrence relation • Today: analyzing recursive algorithms – Solving recurrence relation 11/29/2020 5

Analyzing merge sort T(n) MERGE-SORT A[1. . n] Θ(1) 1. If n = 1, done. 2 T(n/2) 2. Recursively sort A[ 1. . n/2 ] and A[ n/2 +1. . n ]. f(n) 3. “Merge” the 2 sorted lists Sloppiness: Should be T( n/2 ) + T( n/2 ) , but it turns out not to matter asymptotically. 11/29/2020 6

Recurrence for merge sort 1. Divide: Trivial. 2. Conquer: Recursively sort 2 subarrays. 3. Combine: Merge two sorted subarrays T(n) = 2 T(n/2) + Θ(n) # subproblems subproblem size 11/29/2020 Dividing and Combining 7

Binary Search Binary. Search (A[1. . N], value) { if (N == 0) return -1; // not found mid = (1+N)/2; if (A[mid] == value) return mid; // found else if (A[mid] > value) return Binary. Search (A[1. . mid-1], value); else return Binary. Search (A[mid+1, N], value) } 11/29/2020 8

Recursive Insertion Sort Recursive. Insertion. Sort(A[1. . n]) 1. if (n == 1) do nothing; 2. Recursive. Insertion. Sort(A[1. . n-1]); 3. Find index i in A such that A[i] <= A[n] < A[i+1]; 4. Insert A[n] after A[i]; 11/29/2020 9

Compute factorial Factorial (n) if (n == 1) return 1; return n * Factorial (n-1); • Note: here we use n as the size of the input. However, usually for such algorithms we would use log(n), i. e. , the bits needed to represent n, as the input size. 11/29/2020 10

Recurrence for computing power int pow (b, n) m = n >> 1; p = pow (b, m); p = p * p; if (n % 2) return p * b; else return p; T(n) = ? 11/29/2020 int pow (b, n) m = n >> 1; p=pow(b, m)*pow(b, m); if (n % 2) return p * b; else return p; T(n) = ? 11

Recurrence for computing power int pow (b, n) m = n >> 1; p = pow (b, m); p = p * p; if (n % 2) return p * b; else return p; T(n) = T(n/2)+ (1) 11/29/2020 int pow (b, n) m = n >> 1; p=pow(b, m)*pow(b, m); if (n % 2) return p * b; else return p; T(n) = 2 T(n/2)+ (1) 12

What do they mean? Challenge: how to solve the recurrence to get a closed form, e. g. T(n) = Θ (n 2) or T(n) = Θ(nlgn), or at least some bound such as T(n) = O(n 2)? 11/29/2020 13

Solving recurrence • Running time of many algorithms can be expressed in one of the following two recursive forms or Both can be very hard to solve. We focus on relatively easy ones, which you will encounter frequently in many real algorithms (and exams…) 11/29/2020 14

Solving recurrence 1. Recursion tree or iteration method - Good for guessing an answer 2. Substitution method - Generic method, rigid, but may be hard 3. Master method - Easy to learn, useful in limited cases only - Some tricks may help in other cases 11/29/2020 15

Recurrence for merge sort T(n) = (1) if n = 1; 2 T(n/2) + (n) if n > 1. We will usually ignore the base case, assuming it is always a constant (but not 0). 11/29/2020 16

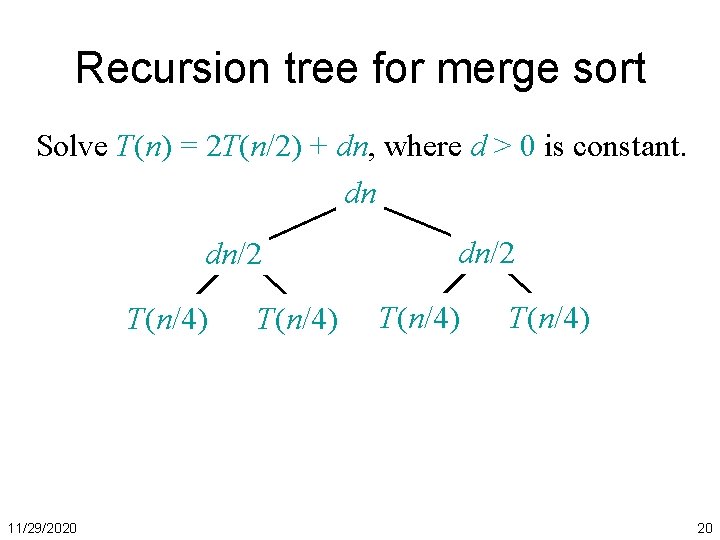
Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. 11/29/2020 17

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. T(n) 11/29/2020 18

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn T(n/2) 11/29/2020 T(n/2) 19

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn/2 T(n/4) 11/29/2020 T(n/4) dn/2 T(n/4) 20

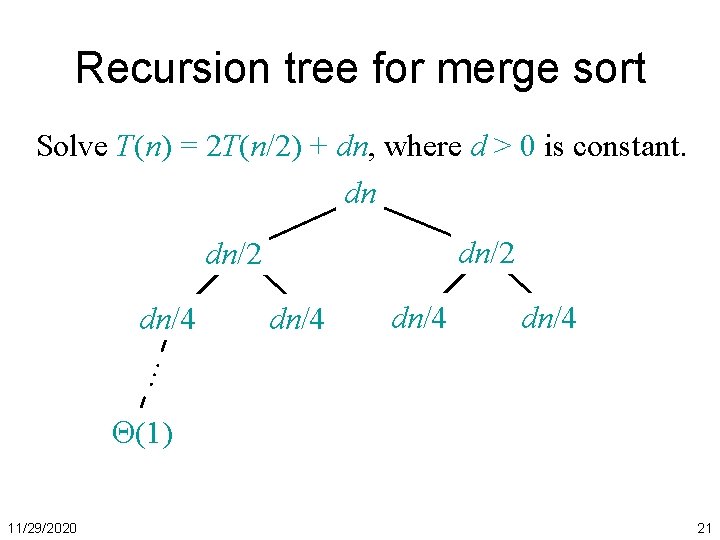
Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn/2 dn/4 … dn/4 (1) 11/29/2020 21

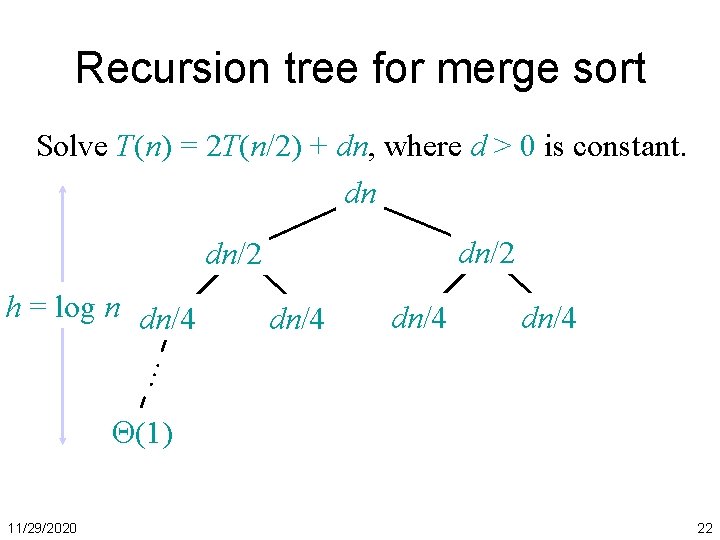
Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn/2 dn/4 … h = log n dn/4 (1) 11/29/2020 22

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 … h = log n dn/4 (1) 11/29/2020 23

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 … h = log n dn/4 dn (1) 11/29/2020 24

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn … h = log n dn/4 dn … dn/2 (1) 11/29/2020 25

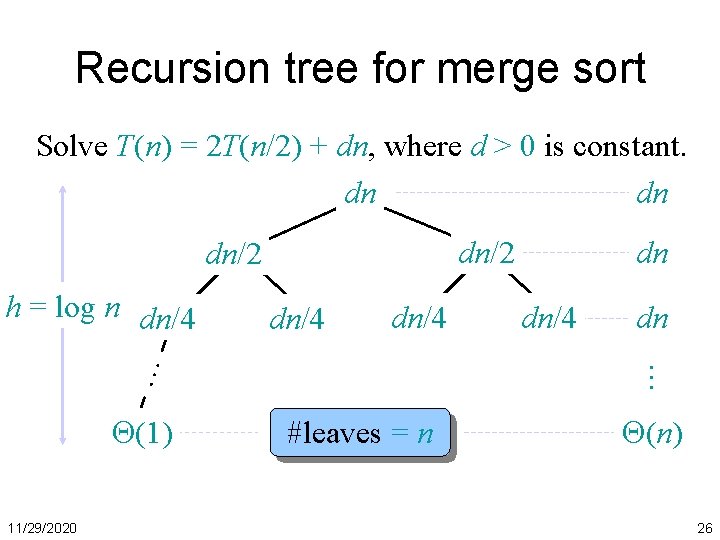
Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 (1) 11/29/2020 dn/4 dn … … h = log n dn/4 dn #leaves = n (n) 26

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 (1) #leaves = n Later we will usually ignore d 11/29/2020 dn/4 dn … … h = log n dn/4 dn (n) Total (n log n) 27

Recurrence for computing power int pow (b, n) m = n >> 1; p = pow (b, m); p = p * p; if (n % 2) return p * b; else return p; T(n) = T(n/2)+ (1) 11/29/2020 int pow (b, n) m = n >> 1; p=pow(b, m)*pow(b, m); if (n % 2) return p * b; else return p; T(n) = 2 T(n/2)+ (1) Which algorithm is more efficient asymptotically? 28

Time complexity for Alg 1 Solve T(n) = T(n/2) + 1 • T(n) = T(n/2) + 1 = T(n/4) + 1 = T(n/8) + 1 + 1 = T(1) + 1 + … + 1 = Θ (log(n)) log(n) Iteration method 11/29/2020 29

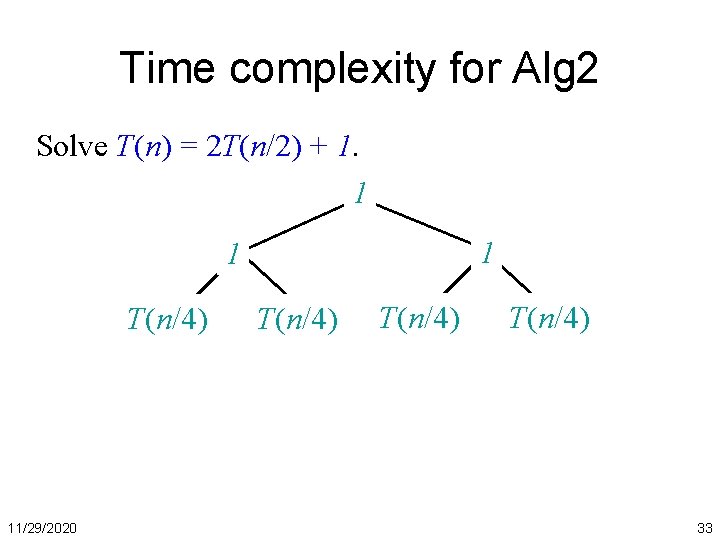
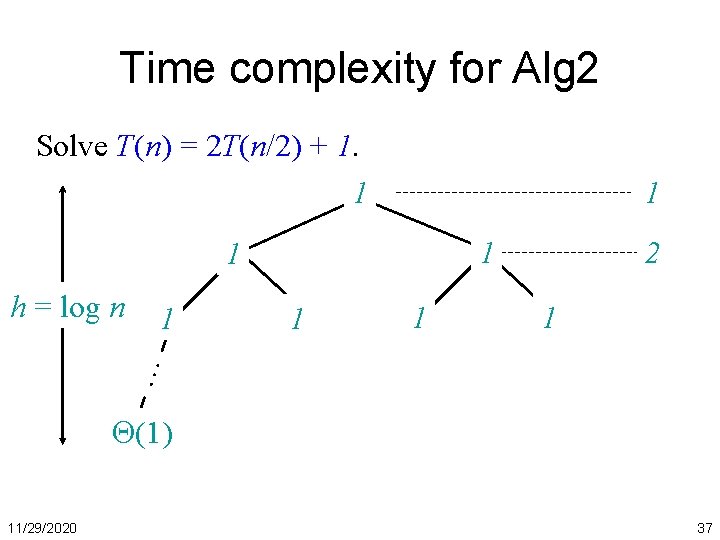
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 11/29/2020 30

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. T(n) 11/29/2020 31

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 T(n/2) 11/29/2020 T(n/2) 32

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 T(n/4) 11/29/2020 T(n/4) 33

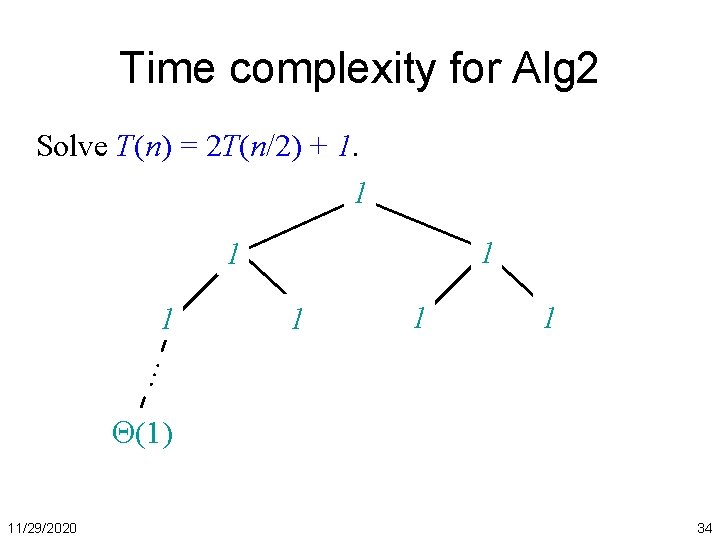
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 … 1 (1) 11/29/2020 34

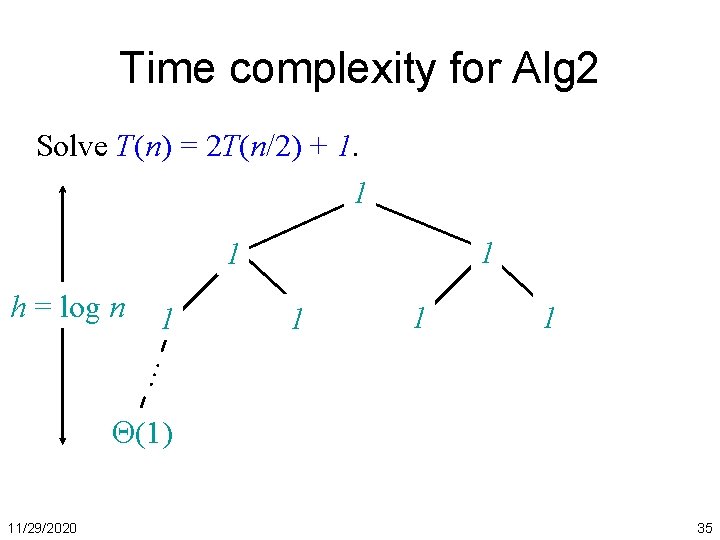
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 1 … h = log n (1) 11/29/2020 35

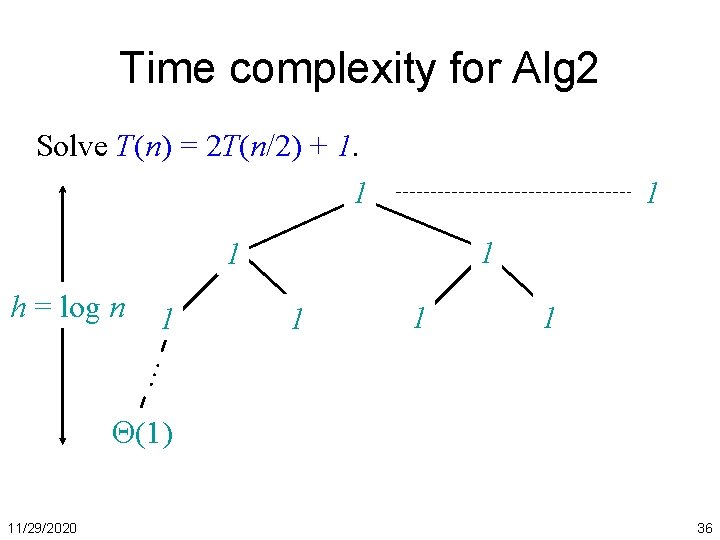
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 1 … h = log n (1) 11/29/2020 36

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 1 … h = log n 2 (1) 11/29/2020 37

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 … h = log n 1 1 2 1 4 … 1 1 (1) 11/29/2020 38

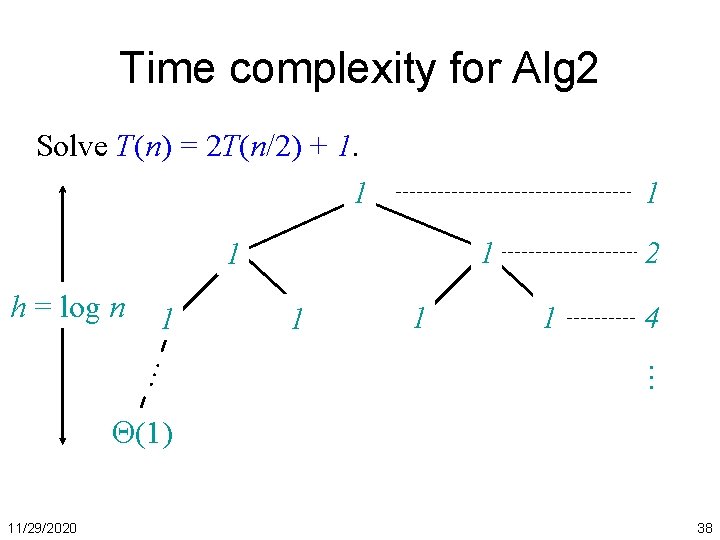
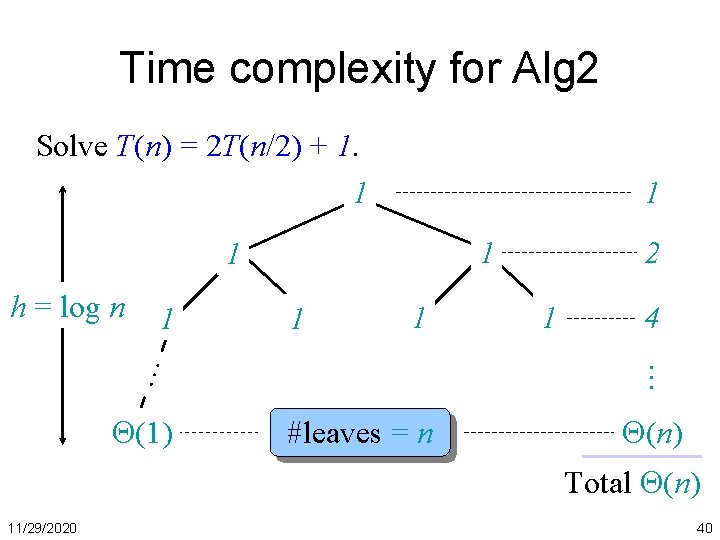
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 1 (1) 11/29/2020 1 4 … … h = log n 2 #leaves = n (n) 39

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 1 (1) 1 4 … … h = log n 2 #leaves = n (n) Total (n) 11/29/2020 40

More iteration method examples • T(n) = T(n-1) + 1 = T(n-2) + 1 = T(n-3) + 1 + 1 = T(1) + 1 + … + 1 = Θ (n) 11/29/2020 n-1 41

More iteration method examples • T(n) = T(n-1) + n = T(n-2) + (n-1) + n = T(n-3) + (n-2) + (n-1) + n = T(1) + 2 + 3 + … + n = Θ (n 2) 11/29/2020 42

3 -way-merge-sort (A[1. . n]) If (n <= 1) return; 3 -way-merge-sort(A[1. . n/3]); 3 -way-merge-sort(A[n/3+1. . 2 n/3]); 3 -way-merge-sort(A[2 n/3+1. . n]); Merge A[1. . n/3] and A[n/3+1. . 2 n/3]; Merge A[1. . 2 n/3] and A[2 n/3+1. . n]; • Is this algorithm correct? • What’s the recurrence function for the running time? • What does the recurrence function solve to? 11/29/2020 43

Unbalanced-merge-sort ub-merge-sort (A[1. . n]) if (n<=1) return; ub-merge-sort(A[1. . n/3]); ub-merge-sort(A[n/3+1. . n]); Merge A[1. . n/3] and A[n/3+1. . n]. • Is this algorithm correct? • What’s the recurrence function for the running time? • What does the recurrence function solve to? 11/29/2020 44

More recursion tree examples (1) • • • T(n) = 3 T(n/3) + n T(n) = T(n/3) + T(2 n/3) + n T(n) = 2 T(n/4) + n 2 T(n) = 3 T(n/2) + n 2 11/29/2020 45

More recursion tree examples (2) • • T(n) = T(n-2) + n T(n) = T(n-2) + 1 T(n) = 2 T(n-2) + n T(n) = 2 T(n-2) + 1 11/29/2020 46