CS 3343 Analysis of Algorithms Lecture 3 Asymptotic















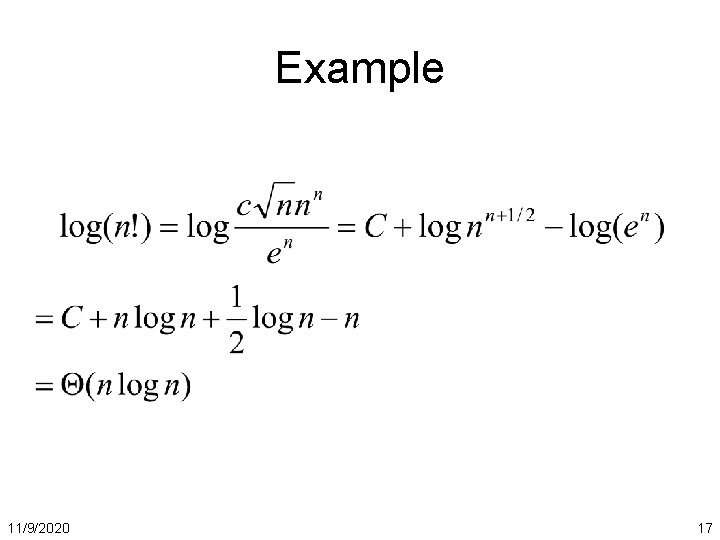















![• Best case – A[1] = A[2] – T(n) = Θ (1) • • Best case – A[1] = A[2] – T(n) = Θ (1) •](https://slidetodoc.com/presentation_image_h/76e36e63ab3973b8291cae41d3e96196/image-33.jpg)













- Slides: 46

CS 3343: Analysis of Algorithms Lecture 3: Asymptotic Notations, Analyzing non-recursive algorithms 11/9/2020 1

Outline • Review of last lecture • Continue on asymptotic notations • Analyzing non-recursive algorithms 11/9/2020 2

Mathematical definitions • O(g(n)) = {f(n): positive constants c and n 0 such that 0 ≤ f(n) ≤ cg(n) n≥n 0} • Ω(g(n)) = {f(n): positive constants c and n 0 such that 0 ≤ cg(n) ≤ f(n) n≥n 0} • Θ(g(n)) = {f(n): positive constants c 1, c 2, and n 0 such that 0 c 1 g(n) f(n) c 2 g(n) n n 0} 11/9/2020 3

Big-Oh • Claim: f(n) = 3 n 2 + 10 n + 5 O(n 2) • Proof by definition: (Hint: Need to find c and n 0 such that f(n) <= cn 2 for all n ≥ n 0. You can be sloppy about the constant factors. Pick a comfortably large c when proving big-O or small one when proving big-Omega. ) (Note: you just need to find one concrete example of c and n 0, but the condition needs to be met for all n ≥ n 0. So do not try to plug in a concrete value of n and show the inequality holds. ) Proof: 3 n 2 + 10 n + 5 3 n 2 + 10 n 2 + 5, n ≥ 1 3 n 2 + 10 n 2 + 5 n 2, n ≥ 1 18 n 2, n ≥ 1 If we let c = 18 and n 0 = 1, we have f(n) c n 2, n ≥ n 0. Therefore by definition 3 n 2 + 10 n + 5 O(n 2). 11/9/2020 4

How to prove logn < n Let f(n) = 1 + log n, g(n) = n. Then f(n)’ = 1/n g(n)’ = 1. f(1) = g(1) = 1. Because f(n)’ ≤ g(n)’ n ≥ 1, by the racetrack principle, we have f(n) ≤ g(n) n ≥ 1, i. e. , 1 + log n ≤ n. Therefore, log n < 1 + log n ≤ n for all n From now on, we will use that fact that log n < n n ≥ 1 without proof. 11/9/2020 5

True or false? 1. 2. 3. 4. 5. 6. 11/9/2020 2 n 2 + 1 = O(n 2) T (also ) Sqrt(n) = O(log n) F ( ) log n = O(sqrt(n)) T (also o) n 2(1 + sqrt(n)) = O(n 2 log n) F ( ) 3 n 2 + sqrt(n) = O(n 2) T (also ) sqrt(n) log n = O(n) T (also o) 6

True or false? 1. 2. 3. 4. 5. 6. 11/9/2020 2 n 2 + 1 = O(n 2) T (also ) Sqrt(n) = O(log n) F ( ) log n = O(sqrt(n)) T (also o) n 2(1 + sqrt(n)) = O(n 2 log n) F ( ) 3 n 2 + sqrt(n) = O(n 2) T (also ) sqrt(n) log n = O(n) T (also o) 7

Questions • If f(n) O(g(n)) 1. compare f(n) and f(n) + g(n) 2. compare g(n) and f(n) + g(n) 3. compare h(n) f(n) and h(n) g(n) where h(n) > 0. • 11/9/2020 How about f(n) Ω (g(n)) and f(n) Θ (g(n))? 8

Asymptotic notations • • • O: <= o: < Ω: >= ω: > Θ: = (in terms of growth rate) 11/9/2020 9

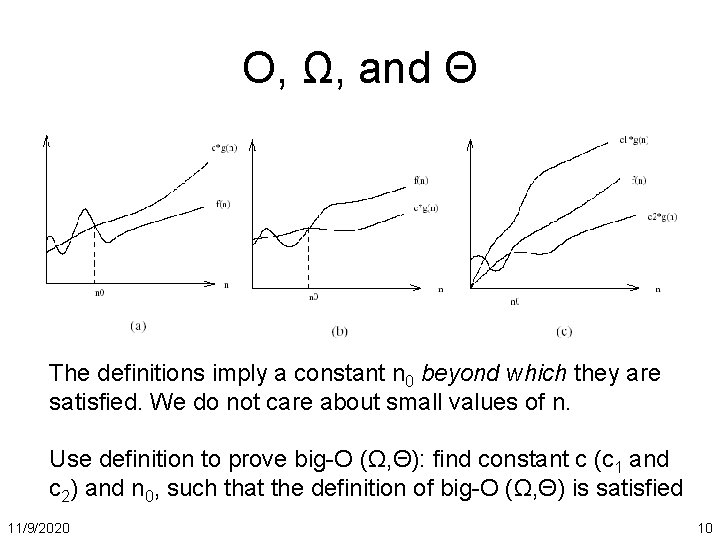
O, Ω, and Θ The definitions imply a constant n 0 beyond which they are satisfied. We do not care about small values of n. Use definition to prove big-O (Ω, Θ): find constant c (c 1 and c 2) and n 0, such that the definition of big-O (Ω, Θ) is satisfied 11/9/2020 10

Use limits to compare orders of growth f(n) o(g(n)) • lim f(n) / g(n) = n→∞ 0 c >0 ∞ f(n) O(g(n)) f(n) Θ (g(n)) f(n) Ω(g(n)) f(n) ω (g(n)) 11/9/2020 11

Examples • Compare 2 n and 3 n n / 3 n = lim(2/3)n = 0 • lim 2 n→∞ • Therefore, 2 n o(3 n), and 3 n ω(2 n) • How about 2 n and 2 n+1? 2 n / 2 n+1 = ½, therefore 2 n = Θ (2 n+1) 11/9/2020 12

L’ Hopital’s rule lim f(n) / g(n) = lim f(n)’ / g(n)’ n→∞ 11/9/2020 n→∞ Condition: If both lim f(n) and lim g(n) = or 0 13

Example • Compare n 0. 5 and log n • lim n 0. 5 / log n = ? n→∞ • • • 11/9/2020 (n 0. 5)’ = 0. 5 n-0. 5 (log n)’ = 1 / n lim (n-0. 5 / 1/n) = lim(n 0. 5) = ∞ Therefore, log n o(n 0. 5) In fact, log n o(nε), for any ε > 0 14

Stirling’s formula or (constant) 11/9/2020 15

Examples • Compare 2 n and n! • Therefore, 2 n = o(n!) • Compare nn and n! • Therefore, nn = ω(n!) • How about log (n!)? 11/9/2020 16
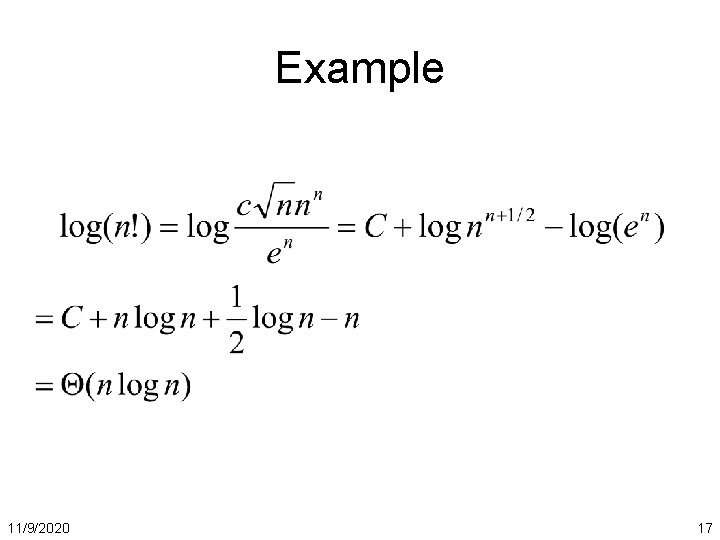
Example 11/9/2020 17

Properties of asymptotic notations • Textbook page 51 • Transitivity f(n) = (g(n)) and g(n) = (h(n)) => f(n) = (h(n)) (holds true for o, O, , and as well). • Symmetry f(n) = (g(n)) if and only if g(n) = (f(n)) • Transpose symmetry f(n) = O(g(n)) if and only if g(n) = (f(n)) f(n) = o(g(n)) if and only if g(n) = (f(n)) 11/9/2020 18

About exponential and logarithm functions • Textbook page 55 -56 • It is important to understand what logarithms are and where they come from. • A logarithm is simply an inverse exponential function. • Saying bx = y is equivalent to saying that x = logb y. • Logarithms reflect how many times we can double something until we get to n, or halve something until we get to 1. • log 21 = ? • log 22 = ? 11/9/2020 19

Binary Search • In binary search we throw away half the possible number of keys after each comparison. • How many times can we halve n before getting to 1? • Answer: ceiling (lg n) 11/9/2020 20

Logarithms and Trees • How tall a binary tree do we need until we have n leaves? • The number of potential leaves doubles with each level. • How many times can we double 1 until we get to n? • Answer: ceiling (lg n) 11/9/2020 21

Logarithms and Bits • How many numbers can you represent with k bits? • Each bit you add doubles the possible number of bit patterns • You can represent from 0 to 2 k – 1 with k bits. A total of 2 k numbers. • How many bits do you need to represent the numbers from 0 to n? • ceiling (lg (n+1)) 11/9/2020 22

logarithms • • 11/9/2020 lg n = log 2 n ln n = loge n, e ≈ 2. 718 lgkn = (lg n)k lg lg n = lg (lg n) = lg(2)n lg(k) n = lg lg lg … lg n lg 24 = ? lg(2)4 = ? Compare lgkn vs lg(k)n? 23

Useful rules for logarithms For all a > 0, b > 0, c > 0, the following rules hold • logba = logca / logcb = lg a / lg b • logban = n logba = a b • • log (ab) = log a + log b – lg (2 n) = ? • log (a/b) = log (a) – log(b) – lg (n/2) = ? – lg (1/n) = ? • logba = 1 / logab 11/9/2020 24

Useful rules for exponentials • For all a > 0, b > 0, c > 0, the following rules hold • a 0 = 1 (00 = ? ) • a 1 = a • a-1 = 1/a • (am)n = amn • (am)n = (an)m • aman = am+n 11/9/2020 25

More advanced dominance ranking 11/9/2020 26

Analyzing the complexity of an algorithm 11/9/2020 27

Kinds of analyses • Worst case – Provides an upper bound on running time • Best case – not very useful, can always cheat • Average case – Provides the expected running time – Very useful, but treat with care: what is “average”? 11/9/2020 28

General plan for analyzing time efficiency of a non-recursive algorithm • Decide parameter (input size) • Identify most executed line (basic operation) • worst-case = average-case? • T(n) = i ti • T(n) = Θ (f(n)) 11/9/2020 29

Example repeated. Element (A, n) // determines whether all elements in a given // array are distinct for i = 1 to n-1 { for j = i+1 to n { if (A[i] == A[j]) return true; } } return false; 11/9/2020 30

Example repeated. Element (A, n) // determines whether all elements in a given // array are distinct for i = 1 to n-1 { for j = i+1 to n { if (A[i] == A[j]) return true; } } return false; 11/9/2020 31

• Best case? • Worst-case? • Average case? 11/9/2020 32
![Best case A1 A2 Tn Θ 1 • Best case – A[1] = A[2] – T(n) = Θ (1) •](https://slidetodoc.com/presentation_image_h/76e36e63ab3973b8291cae41d3e96196/image-33.jpg)
• Best case – A[1] = A[2] – T(n) = Θ (1) • Worst-case – No repeated elements – T(n) = (n-1) + (n-2) + … + 1 = n (n-1) / 2 = Θ (n 2) • Average case? – What do you mean by “average”? – Need more assumptions about data distribution. • How many possible repeats are in the data? – Average-case analysis often involves probability. 11/9/2020 33

Find the order of growth for sums • • • T(n) = i=1. . n i = Θ (n 2) T(n) = i=1. . n log (i) = ? T(n) = i=1. . n n / 2 i = ? T(n) = i=1. . n 2 i = ? … • How to find out the actual order of growth? – Math… – Textbook Appendix A. 1 (page 1058 -60) 11/9/2020 34

Arithmetic series • An arithmetic series is a sequence of numbers such that the difference of any two successive members of the sequence is a constant. e. g. : 1, 2, 3, 4, 5 or 10, 12, 14, 16, 18, 20 • In general: Recursive definition Or: 11/9/2020 Closed form, or explicit formula 35

Sum of arithmetic series If a 1, a 2, …, an is an arithmetic series, then e. g. 1 + 3 + 5 + 7 + … + 99 = ? (series definition: ai = 2 i-1) This is ∑ i = 1 to 50 (ai) = 50 * (1 + 99) / 2 = 2500 11/9/2020 36

Geometric series • A geometric series is a sequence of numbers such that the ratio between any two successive members of the sequence is a constant. e. g. : 1, 2, 4, 8, 16, 32 or 10, 20, 40, 80, 160 or 1, ½, ¼, 1/8, 1/16 • In general: Recursive definition Or: 11/9/2020 Closed form, or explicit formula 37

Sum of geometric series if r < 1 if r > 1 if r = 1 11/9/2020 38

Sum of geometric series if r < 1 if r > 1 if r = 1 11/9/2020 39

Important formulas 11/9/2020 40

Sum manipulation rules Example: 11/9/2020 41

Sum manipulation rules Example: 11/9/2020 42

• i=1. . n n / 2 i = n * i=1. . n (½)i = ? • using the formula for geometric series: i=0. . n (½)i = 1 + ½ + ¼ + … (½)n = 2 • Application: algorithm for allocating dynamic memories 11/9/2020 43

• i=1. . n log (i) = log 1 + log 2 + … + log n = log 1 x 2 x 3 x … x n = log n! = (n log n) • Application: algorithm for selection sort using priority queue 11/9/2020 44

Recursive definition of sum of series • T (n) = i=0. . n i is equivalent to: Recurrence T(n) = T(n-1) + n Boundary condition T(0) = 0 • T(n) = i=0. . n ai is equivalent to: T(n) = T(n-1) + an T(0) = 1 Recursive definition is often intuitive and easy to obtain. It is very useful in analyzing recursive algorithms, and some non-recursive algorithms too. 11/9/2020 45

Recursive definition of sum of series • How to solve such recurrence or more generally, recurrence in the form of: • T(n) = a. T(n-b) + f(n) or • T(n) = a. T(n/b) + f(n) 11/9/2020 46
 Analysis of algorithms lecture notes
Analysis of algorithms lecture notes Asymptotic complexity examples
Asymptotic complexity examples Asymptotic analysis
Asymptotic analysis Little omega
Little omega Introduction to algorithms lecture notes
Introduction to algorithms lecture notes 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Asimtotik adalah
Asimtotik adalah Pengertian kompleksitas algoritma
Pengertian kompleksitas algoritma Aep information theory
Aep information theory Asymptotic run time
Asymptotic run time Asymptotic growth rate
Asymptotic growth rate Lower bounds for sorting
Lower bounds for sorting Notasi omega
Notasi omega Asymptotically tight bound
Asymptotically tight bound Asymptotic notation graph
Asymptotic notation graph Asymptotic freedom
Asymptotic freedom Growth of functions
Growth of functions Small omega notation
Small omega notation 1001 design
1001 design An introduction to the analysis of algorithms
An introduction to the analysis of algorithms How to analyze algorithm
How to analyze algorithm Association analysis: basic concepts and algorithms
Association analysis: basic concepts and algorithms Input and output algorithm
Input and output algorithm Algorithm analysis examples
Algorithm analysis examples Algorithm analysis examples
Algorithm analysis examples Mathematical analysis of non-recursive algorithms
Mathematical analysis of non-recursive algorithms Cluster analysis: basic concepts and algorithms
Cluster analysis: basic concepts and algorithms Probabilistic analysis and randomized algorithms
Probabilistic analysis and randomized algorithms Design and analysis of algorithms introduction
Design and analysis of algorithms introduction Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Cjih
Cjih Goals of analysis of algorithms
Goals of analysis of algorithms Exercise 24
Exercise 24 Binary search in design and analysis of algorithms
Binary search in design and analysis of algorithms Introduction to the design and analysis of algorithms
Introduction to the design and analysis of algorithms Competitive analysis algorithms
Competitive analysis algorithms Design and analysis of algorithms
Design and analysis of algorithms Design and analysis of algorithms
Design and analysis of algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Comp 482
Comp 482 Exploratory data analysis lecture notes
Exploratory data analysis lecture notes Sensitivity analysis lecture notes
Sensitivity analysis lecture notes Factor analysis lecture notes
Factor analysis lecture notes Tiu lecture notes medical analysis
Tiu lecture notes medical analysis Zline 667-36
Zline 667-36 Computational thinking algorithms and programming
Computational thinking algorithms and programming Types of algorithm
Types of algorithm