Asymptotic Growth Rate CutlerHead 1 Function Growth The














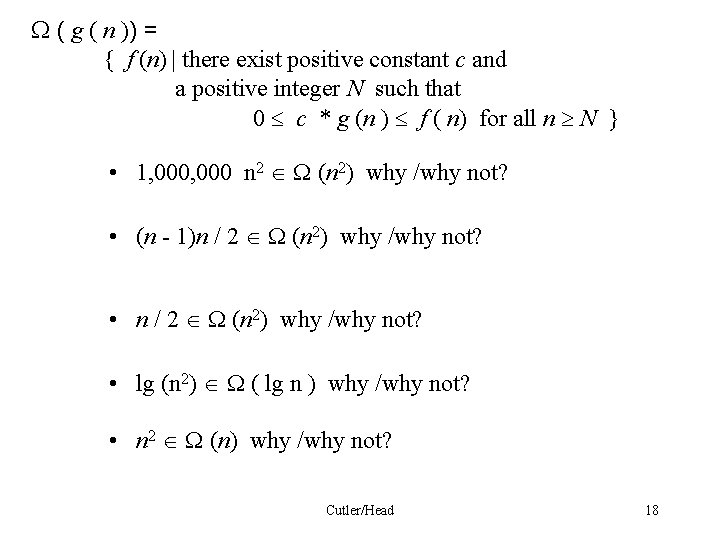


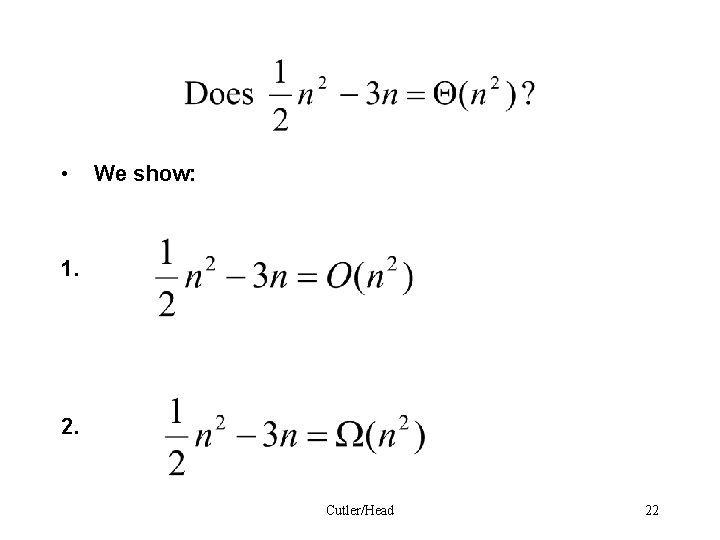

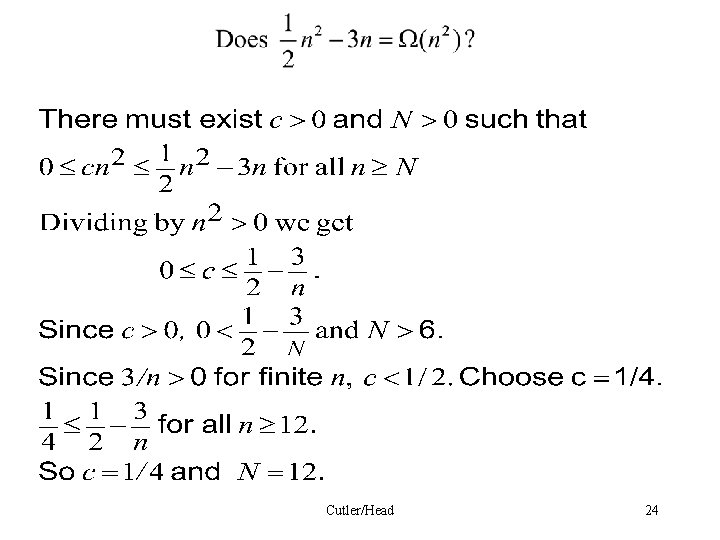
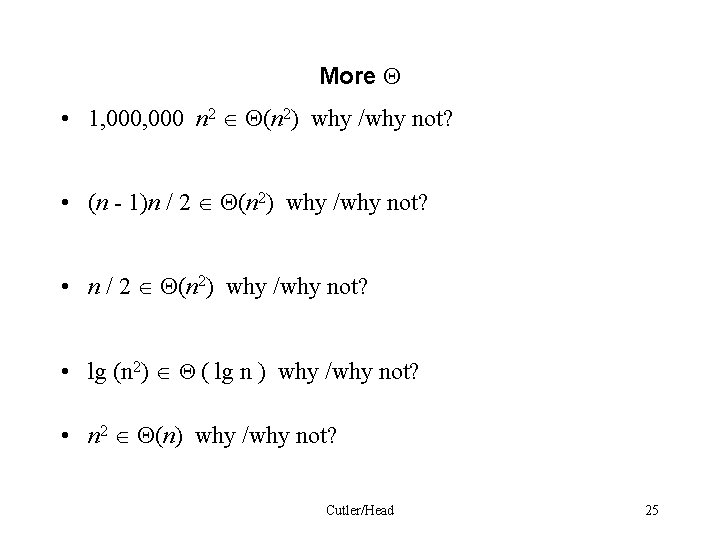





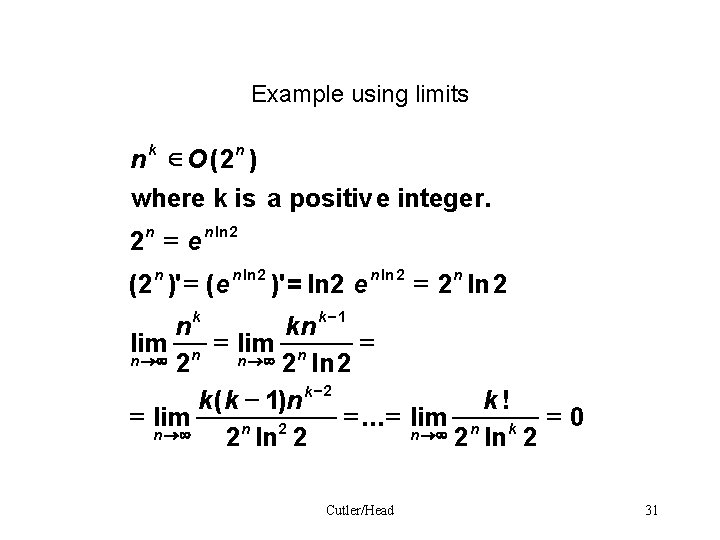





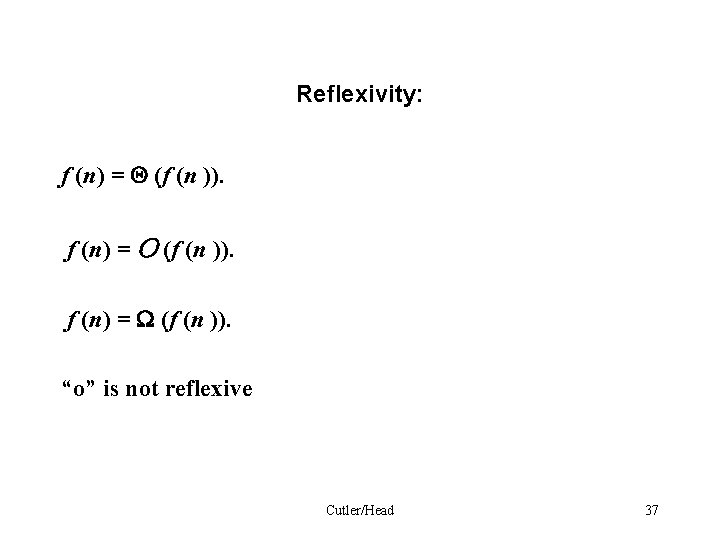
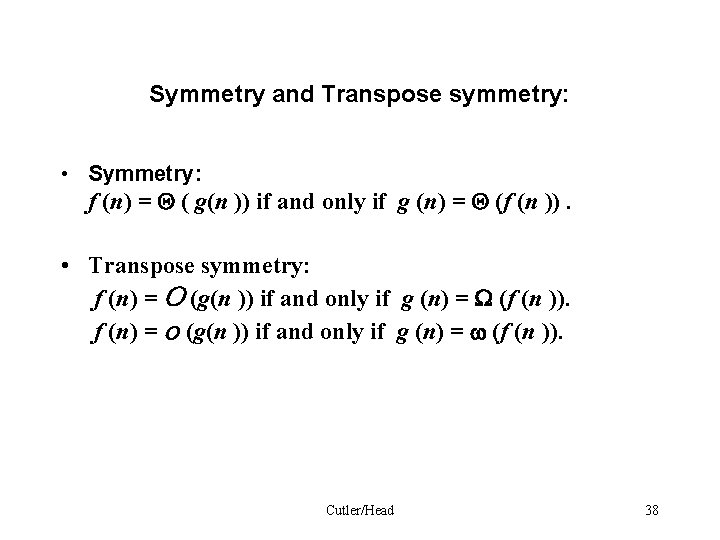




- Slides: 43

Asymptotic Growth Rate Cutler/Head 1

Function Growth • The running time of an algorithm as input size approaches infinity is called the asymptotic running time • We study different notations for asymptotic efficiency. • In particular, we study tight bounds, upper bounds and lower bounds. CS 575 / Class 1 2

Outline • Why do we need the different sets? • Definition of the sets O, Omega and Theta • Classifying examples: – Using the original definition – Using limits • General Properties • Little Oh • Additional properties Cutler/Head 3

The “sets” and their use – big Oh • Big “oh” - asymptotic upper bound on the growth of an algorithm • When do we use Big Oh? 1. Theory of NP-completeness 2. To provide information on the maximum number of operations that an algorithm performs – Insertion sort is O(n 2) in the worst case • This means that in the worst case it performs at most cn 2 operations – Insertion sort is also O(n 6) in the worst case since it also performs at most dn 6 operations Cutler/Head 4

The “sets” and their use – Omega - asymptotic lower bound on the growth of an algorithm or a problem* When do we use Omega? 1. To provide information on the minimum number of operations that an algorithm performs – Insertion sort is (n) in the best case • This means that in the best case its instruction count is at least cn, – It is (n 2) in the worst case • This means that in the worst case its instruction count is at least cn 2 Cutler/Head 5

The “sets” and their use – Omega cont. 2. To provide information on a class of algorithms that solve a problem – Sort algorithms based on comparison of keys are (nlgn) in the worst case • This means that all sort algorithms based only on comparison of keys have to do at least cnlgn operations – Any algorithm based only on comparison of keys to find the maximum of n elements is (n) in every case • This means that all algorithms based only on comparison of keys to find maximum have to do at least cn operations Cutler/Head 6

The “sets” and their use - Theta • Theta - asymptotic tight bound on the growth rate of an algorithm – Insertion sort is (n 2) in the worst and average cases • The means that in the worst case and average cases insertion sort performs cn 2 operations – Binary search is (lg n) in the worst and average cases • The means that in the worst case and average cases binary search performs clgn operations • Note: We want to classify an algorithm using Theta. – In Data Structures used Oh • Little “oh” - used to denote an upper bound that is not asymptotically tight. n is in o(n 3). n is not in o(n) Cutler/Head 7

The functions • Let f(n) and g(n) be asymptotically nonnegative functions whose domains are the set of natural numbers N={0, 1, 2, …}. • A function g(n) is asymptotically nonnegative, if g(n) 0 for all n n 0 where n 0 N CS 575 / Class 1 8

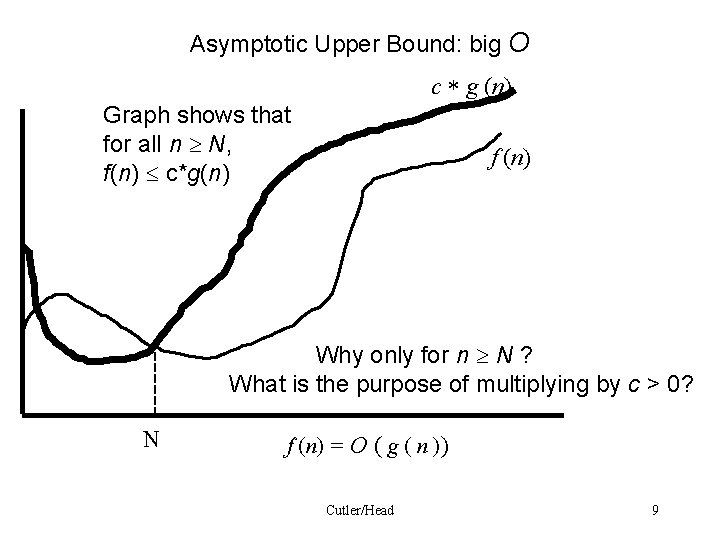
Asymptotic Upper Bound: big O c g (n) Graph shows that for all n N, f(n) c*g(n) f (n) Why only for n N ? What is the purpose of multiplying by c > 0? N f (n) = O ( g ( n )) Cutler/Head 9

Asymptotic Upper Bound: O Definition: Let f (n) and g(n) be asymptotically non-negative functions. We say f (n) is in O ( g ( n )) if there is a real positive constant c and a positive Integer N such that for every n ³ N 0 f (n) c g (n ). Or using more mathematical notation O ( g (n) ) = { f (n )| there exist positive constant c and a positive integer N such that 0 f( n) c g (n ) for all n ³ N } Cutler/Head 10

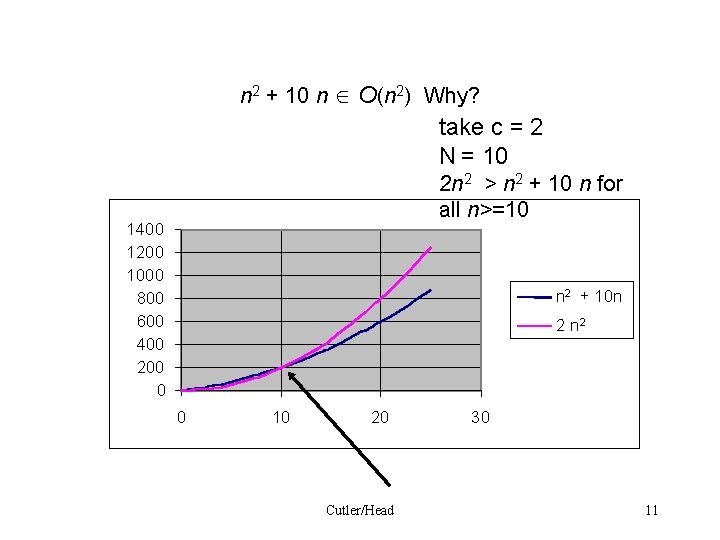
n 2 + 10 n O(n 2) Why? take c = 2 N = 10 2 n 2 > n 2 + 10 n for all n>=10 1400 1200 1000 800 600 400 200 0 n 2 + 10 n 2 0 10 20 Cutler/Head 30 11

Does 5 n+2 O(n)? Proof: From the definition of Big Oh, there must exist c>0 and integer N>0 such that 0 5 n+2 cn for all n N. Dividing both sides of the inequality by n>0 we get: 0 5+2/n c. 2/n 2, 2/n>0 becomes smaller when n increases There are many choices here for c and N. If we choose N=1 then c 5+2/1= 7. If we choose c=6, then 0 5+2/n 6. So N 2. In either case (we only need one!) we have a c>o and N>0 such that 0 5 n+2 cn for all n N. So the definition is satisfied and 5 n+2 O(n) Cutler/Head 12

Does n 2 O(n)? No. We will prove by contradiction that the definition cannot be satisfied. Assume that n 2 O(n). From the definition of Big Oh, there must exist c>0 and integer N>0 such that 0 n 2 cn for all n N. Dividing the inequality by n>0 we get 0 n c for all n N. n c cannot be true for any n >max{c, N }, contradicting our assumption So there is no constant c>0 such that n c is satisfied for all n N, and n 2 O(n) Cutler/Head 13

O ( g (n) ) = { f (n )| there exist positive constant c and positive integer N such that 0 f( n) c g (n ) for all n N } • 1, 000 n 2 O(n 2) why/why not? • (n - 1)n / 2 O(n 2) why /why not? • lg (n 2) O( lg n ) why /why not? • n 2 O(n) why /why not? Cutler/Head 14

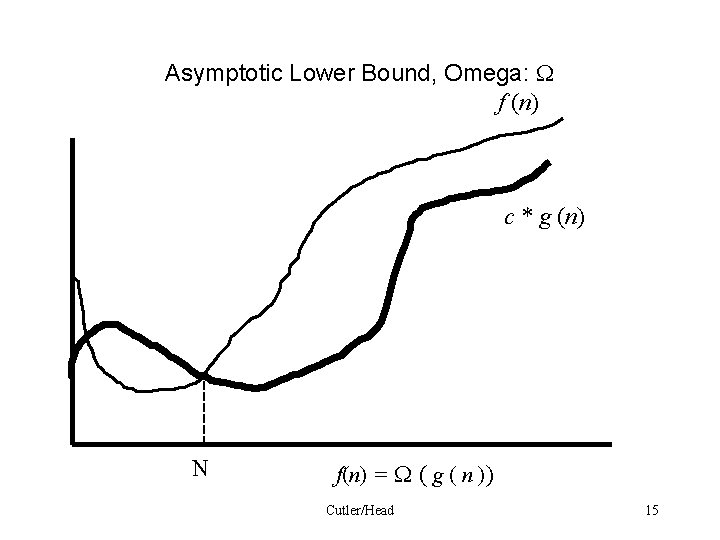
Asymptotic Lower Bound, Omega: f (n) c * g (n) N f(n) = ( g ( n )) Cutler/Head 15

Asymptotic Lower Bound: Definition: Let f (n) and g(n) be asymptotically non-negative functions. We say f (n) is ( g ( n )) if there is a positive real constant c and a positive integer N such that for every n ³ N 0 c * g (n ) f ( n). Or using more mathematical notation ( g ( n )) = { f (n) | there exist positive constant c and a positive integer N such that 0 c * g (n ) f ( n) for all n ³ N } Cutler/Head 16

Is 5 n-20 (n)? Proof: From the definition of Omega, there must exist c>0 and integer N>0 such that 0 cn 5 n-20 for all n N Dividing the inequality by n>0 we get: 0 c 5 -20/n for all n N. 20/n 20, and 20/n becomes smaller as n grows. There are many choices here for c and N. Since c > 0, 5 – 20/n >0 and N >4 For example, if we choose c=4, then 5 – 20/n 4 and N 20 In this case we have a c>o and N>0 such that 0 cn 5 n-20 for all n N. So the definition is satisfied and 5 n-20 (n) Cutler/Head 17
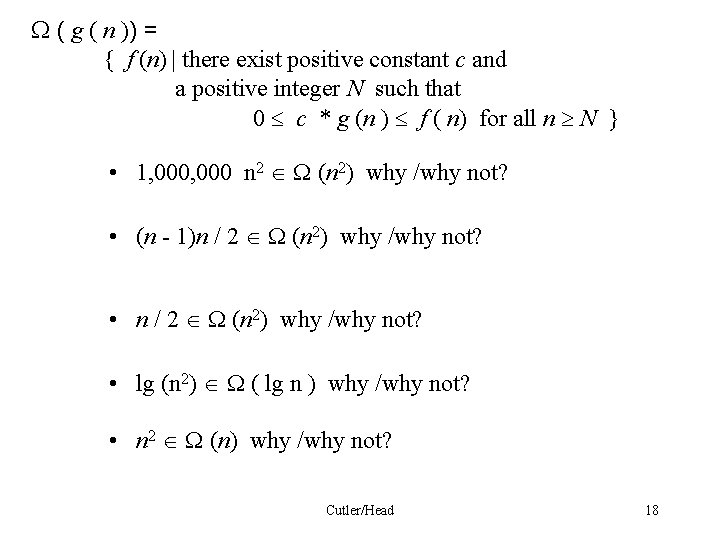
( g ( n )) = { f (n) | there exist positive constant c and a positive integer N such that 0 c * g (n ) f ( n) for all n N } • 1, 000 n 2 (n 2) why /why not? • (n - 1)n / 2 (n 2) why /why not? • lg (n 2) ( lg n ) why /why not? • n 2 (n) why /why not? Cutler/Head 18

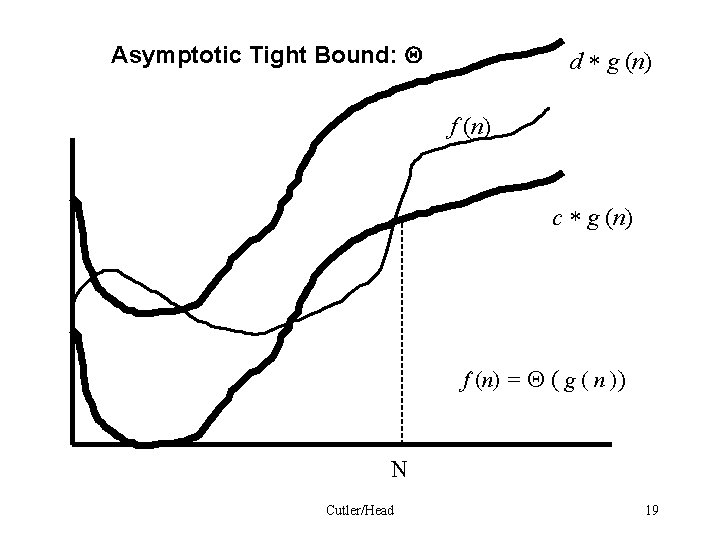
Asymptotic Tight Bound: d g (n) f (n) c g (n) f (n) = ( g ( n )) N Cutler/Head 19

Asymptotic Bound Theta: Definition: Let f (n) and g(n) be asymptotically non-negative functions. We say f (n) is ( g ( n )) if there are positive constants c, d and a positive integer N such that for every n ³ N 0 c g (n ) f ( n) d g ( n ). Or using more mathematical notation ( g ( n )) = { f (n) | there exist positive constants c, d and a positive integer N such that 0 c g (n ) f ( n) d g ( n ). for all n ³ N } Cutler/Head 20

More on • We will use this definition: (g (n)) = O( g (n) ) Ç W ( g (n) ) Cutler/Head 21
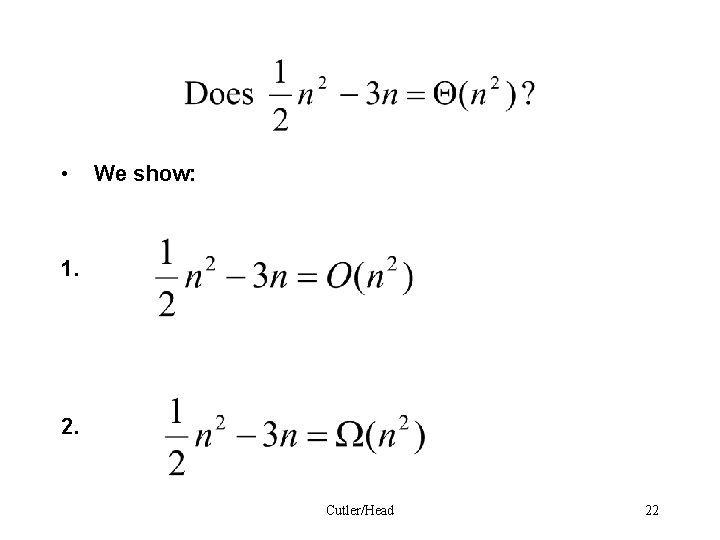
• We show: 1. 2. Cutler/Head 22

Cutler/Head 23
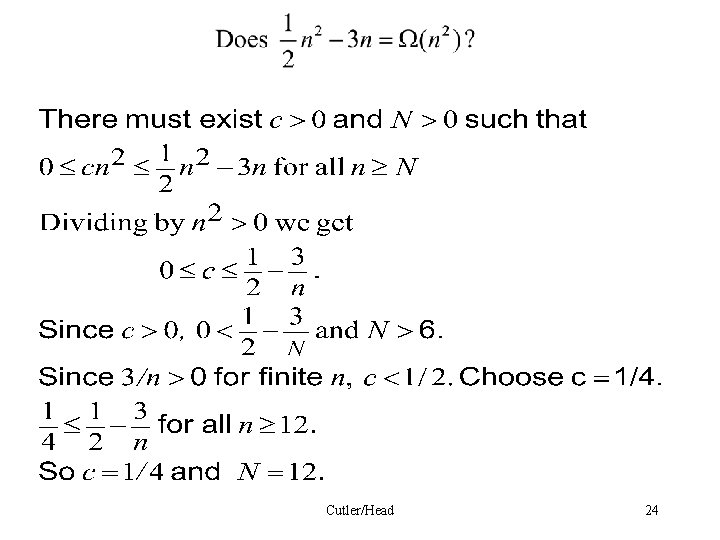
Cutler/Head 24
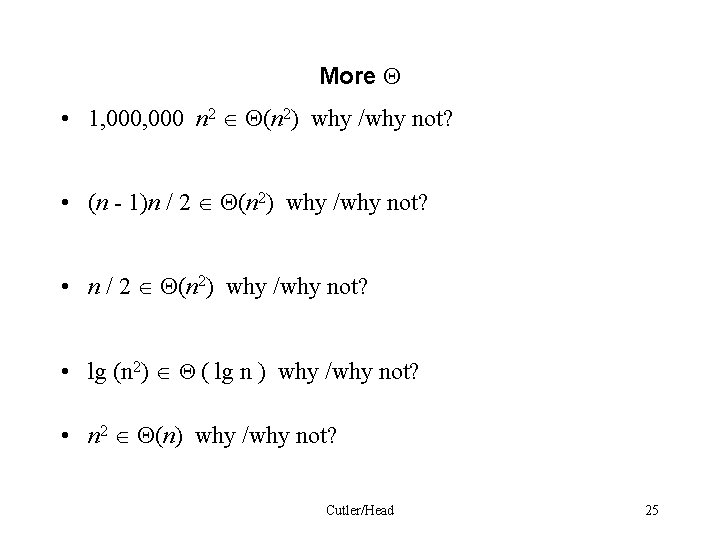
More • 1, 000 n 2 (n 2) why /why not? • (n - 1)n / 2 (n 2) why /why not? • lg (n 2) ( lg n ) why /why not? • n 2 (n) why /why not? Cutler/Head 25

Limits can be used to determine Order { c then f (n) = ( g (n)) if c > 0 if lim f (n) / g (n) = n®¥ 0 or c > 0 then f (n) = o ( g(n)) ¥ or c > 0 then f (n) = ( g (n)) • The limit must exist Cutler/Head 26

Example using limits Cutler/Head 27

L’Hopital’s Rule If f(x) and g(x) are both differentiable with derivatives f’(x) and g’(x), respectively, and if Cutler/Head 28

Example using limits Cutler/Head 29

Example using limits lg n O (n ) ln n lg n = ln 2 æ ln n ö 1 (lg n)' = ç ÷ '= è ln 2 ø nln 2 lg n (lg n)' 1 = lim =0 lim n ®¥ n ln 2 n' Cutler/Head 30
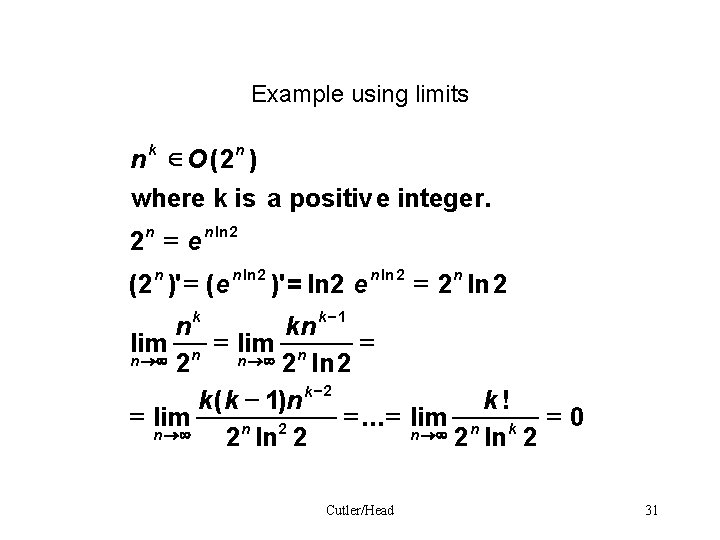
Example using limits n k O (2 n ) where k is a positiv e integer. 2 n = e n ln 2 n = = ( 2 )' (e )'= ln 2 e 2 ln 2 n - nk kn k 1 = lim n n® ¥ 2 n ® ¥ 2 ln 2 k -2 k ( k 1)n k! = lim = =. . . lim n k = 0 2 n n® ¥ n ® ¥ 2 ln 2 Cutler/Head 31

Another upper bound “little oh”: o Definition: Let f (n) and g(n) be asymptotically non-negative functions. . We say f ( n ) is o ( g ( n )) if for every positive real constant c there exists a positive integer N such that for all n ³ N 0 f(n) < c g (n ). o ( g (n) ) = {f(n) : for any positive constant c >0, there exists a positive integer N > 0 such that 0 f( n) < c g (n ) for all n ³ N } • “little omega” can also be defined Cutler/Head 32

main difference between O and o O ( g (n) ) = { f (n )| there exist positive constant c and a positive integer N such that 0 f( n) c g (n ) for all n ³ N } o ( g (n) ) = { f(n) | for any positive constant c >0, there exists a positive integer N such that 0 f( n) < c g (n ) for all n ³ N } For ‘o’ the inequality holds for all positive constants. Whereas for ‘O’ the inequality holds for constants. Cutler/Head some positive 33

Lower-order terms and constants • Lower order terms of a function do not matter since lowerorder terms are dominated by the higher order term. • Constants (multiplied by highest order term) do not matter, since they do not affect the asymptotic growth rate • All logarithms with base b >1 belong to (lg n) since Cutler/Head 34

Asymptotic notation in equations What does n 2 + 2 n + 99 = n 2 + (n) mean? n 2 + 2 n + 99 = n 2 + f(n) Where the function f(n) is from the set (n). In fact f(n) = 2 n + 99. Using notation in this manner can help to eliminate nonaffecting details and clutter in an equation. ? 2 n 2 + 5 n + 21= 2 n 2 + (n ) = (n 2) Cutler/Head 35

Transitivity: If f (n) = (g(n )) and g (n) = (h(n )) then f (n) = (h(n )). If f (n) = O (g(n )) and g (n) = O (h(n )) then f (n) = O (h(n )). If f (n) = W (g(n )) and g (n) = W (h(n )) then f (n) = W (h(n )). If f (n) = o (g(n )) and g (n) = o (h(n )) then f (n) = o (h(n )). If f (n) = w (g(n )) and g (n) = w (h(n )) then f (n) = w (h(n )) Cutler/Head 36
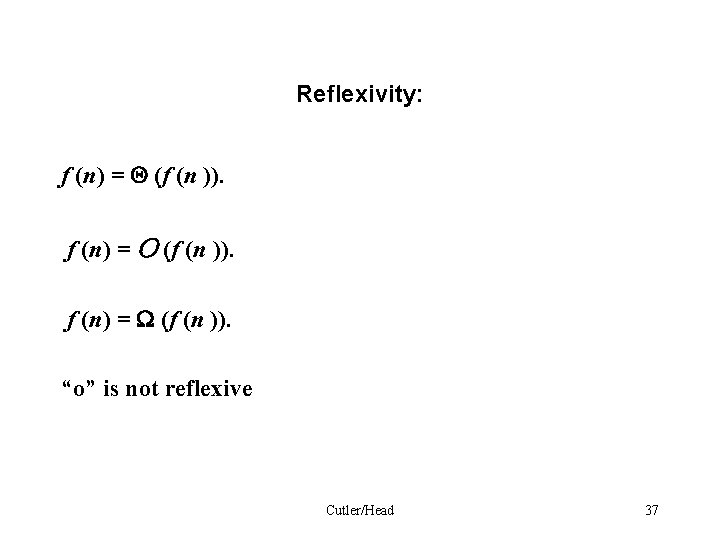
Reflexivity: f (n) = (f (n )). f (n) = O (f (n )). f (n) = W (f (n )). “o” is not reflexive Cutler/Head 37
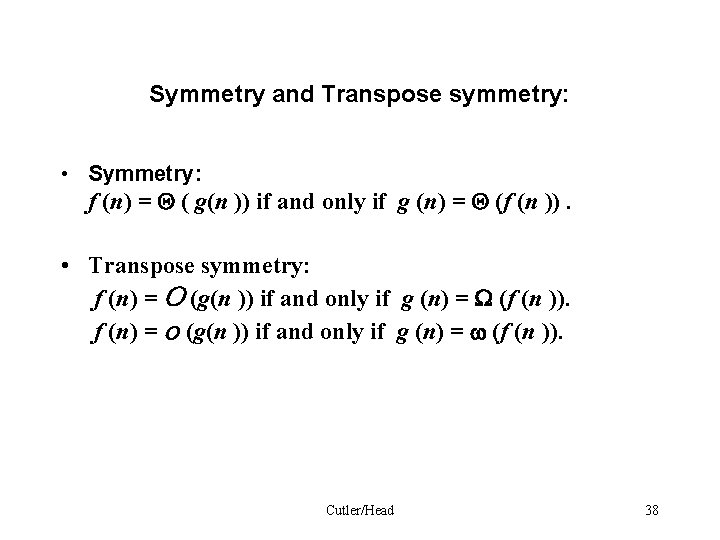
Symmetry and Transpose symmetry: • Symmetry: f (n) = ( g(n )) if and only if g (n) = (f (n )). • Transpose symmetry: f (n) = O (g(n )) if and only if g (n) = W (f (n )). f (n) = o (g(n )) if and only if g (n) = w (f (n )). Cutler/Head 38

Analogy between asymptotic comparison of functions and comparison of real numbers. f (n) = O( g(n)) f (n) = W ( g(n)) f (n) = o ( g(n)) f (n) = w ( g(n)) » » » Cutler/Head a b a³b a=b a<b a>b 39

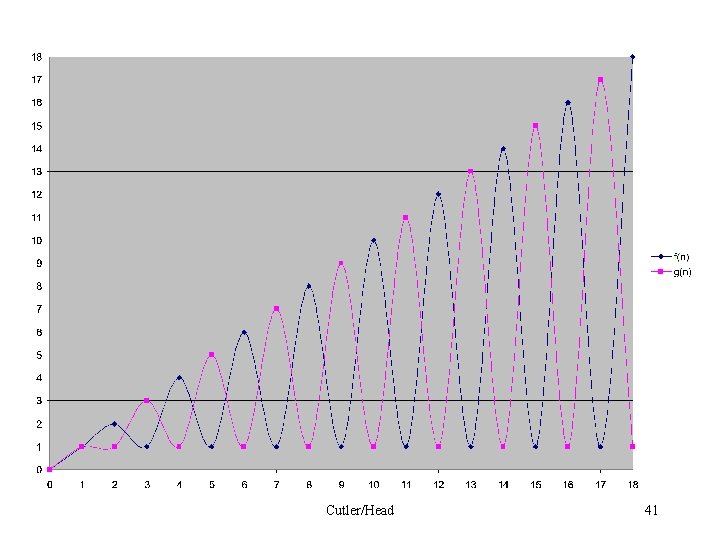
Not All Functions are Comparable The following functions are not asymptotically comparable: Cutler/Head 40

Cutler/Head 41

Is O(g(n)) = (g(n)) o(g(n))? We show a counter example: The functions are: g(n) = n and f(n) O(n) but f(n) and f(n) o(n) Conclusion: O(g(n)) o(g(n)) Cutler/Head 42

General Rules • We say a function f (n ) is polynomially bounded if f (n ) = O ( nk ) for some positive constant k • We say a function f (n ) is polylogarithmic bounded if f (n ) = O ( lgk n) for some positive constant k • Exponential functions – grow faster than positive polynomial functions – grow faster than polylogarithmic functions Cutler/Head 43