CS 3343 Analysis of Algorithms Lecture 2 Asymptotic















![What can S be? Inner loop stops when A[i] <= key, or i = What can S be? Inner loop stops when A[i] <= key, or i =](https://slidetodoc.com/presentation_image_h/04e6a62291833cf2e25209601efcba47/image-21.jpg)
![Best case Inner loop stops when A[i] <= key, or i = 0 i Best case Inner loop stops when A[i] <= key, or i = 0 i](https://slidetodoc.com/presentation_image_h/04e6a62291833cf2e25209601efcba47/image-22.jpg)
![Worst case Inner loop stops when A[i] <= key i j 1 sorted • Worst case Inner loop stops when A[i] <= key i j 1 sorted •](https://slidetodoc.com/presentation_image_h/04e6a62291833cf2e25209601efcba47/image-23.jpg)
![Average case Inner loop stops when A[i] <= key i j 1 sorted • Average case Inner loop stops when A[i] <= key i j 1 sorted •](https://slidetodoc.com/presentation_image_h/04e6a62291833cf2e25209601efcba47/image-24.jpg)

























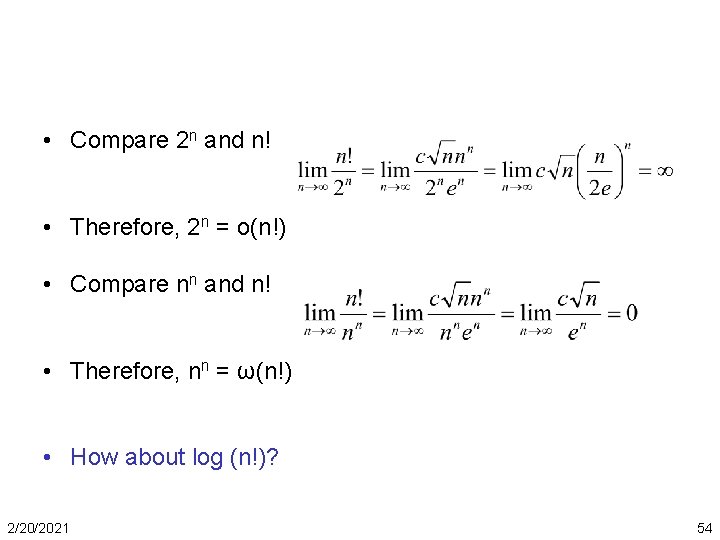
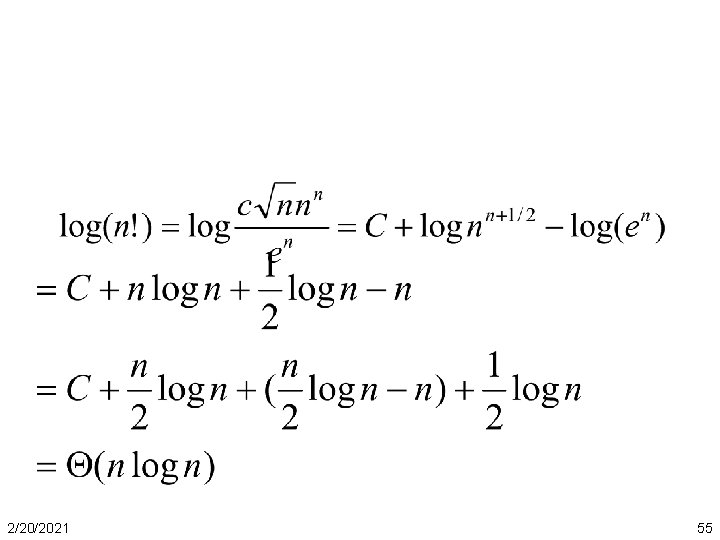


- Slides: 57

CS 3343: Analysis of Algorithms Lecture 2: Asymptotic Notations 2/20/2021 1

Outline • Review of last lecture • Order of growth • Asymptotic notations – Big O, big Ω, Θ 2/20/2021 2

How to express algorithms? Increasing precision Nature language (e. g. English) Pseudocode Real programming languages Ease of expression Describe the ideas of an algorithm in nature language. Use pseudocode to clarify sufficiently tricky details of the algorithm. 2/20/2021 3

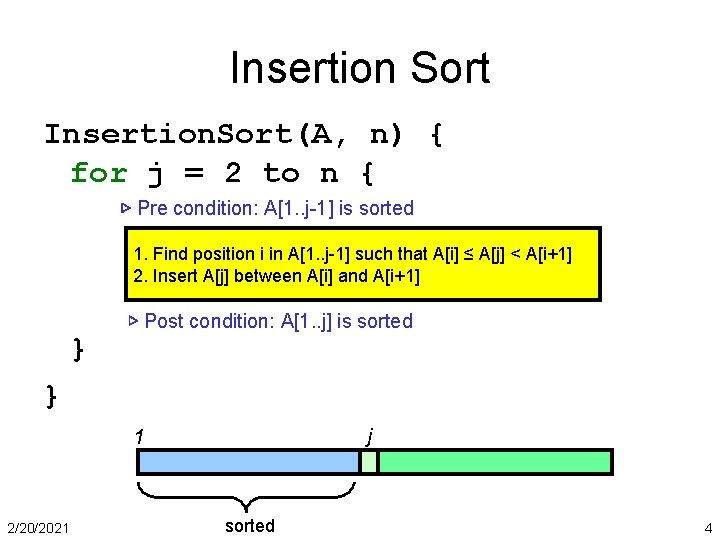
Insertion Sort Insertion. Sort(A, n) { for j = 2 to n { ▷ Pre condition: A[1. . j-1] is sorted 1. Find position i in A[1. . j-1] such that A[i] ≤ A[j] < A[i+1] 2. Insert A[j] between A[i] and A[i+1] } ▷ Post condition: A[1. . j] is sorted } j 1 2/20/2021 sorted 4

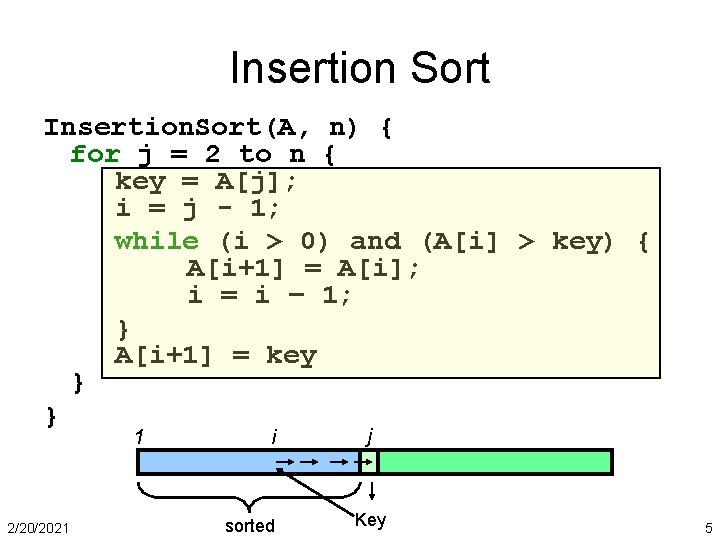
Insertion Sort Insertion. Sort(A, n) { for j = 2 to n { key = A[j]; i = j - 1; while (i > 0) and (A[i] > key) { A[i+1] = A[i]; i = i – 1; } A[i+1] = key } } 1 2/20/2021 i sorted j Key 5

Use loop invariants to prove the correctness of loops • A loop invariant (LI) is a formal statement about the variables in your program which holds true throughout the loop • Proof by induction – Initialization: the LI is true prior to the 1 st iteration – Maintenance: if the LI is true before the jth iteration, it remains true before the (j+1)th iteration – Termination: when the loop terminates, the invariant shows the correctness of the algorithm 2/20/2021 6

Loop invariants and correctness of insertion sort • Claim: at the start of each iteration of the for loop, the subarray consists of the elements originally in A[1. . j-1] but in sorted order. • Proof: by induction 2/20/2021 7

Prove correctness using loop invariants Insertion. Sort(A, n) { for j = 2 to n { key = A[j]; i = j - 1; ▷Insert A[j] into the sorted sequence A[1. . j-1] } } 2/20/2021 while (i > 0) and (A[i] > key) { A[i+1] = A[i]; i = i – 1; } A[i+1] = key Loop invariant: at the start of each iteration of the for loop, the subarray A[1. . j-1] consists of the elements originally in A[1. . j-1] but in sorted order. 8

Initialization Insertion. Sort(A, n) { for j = 2 to n { key = A[j]; i = j - 1; Subarray A[1] is sorted. So loop invariant is true before the loop starts. ▷Insert A[j] into the sorted sequence A[1. . j-1] } while (i > 0) and (A[i] > key) { A[i+1] = A[i]; i = i – 1; } A[i+1] = key } 2/20/2021 9

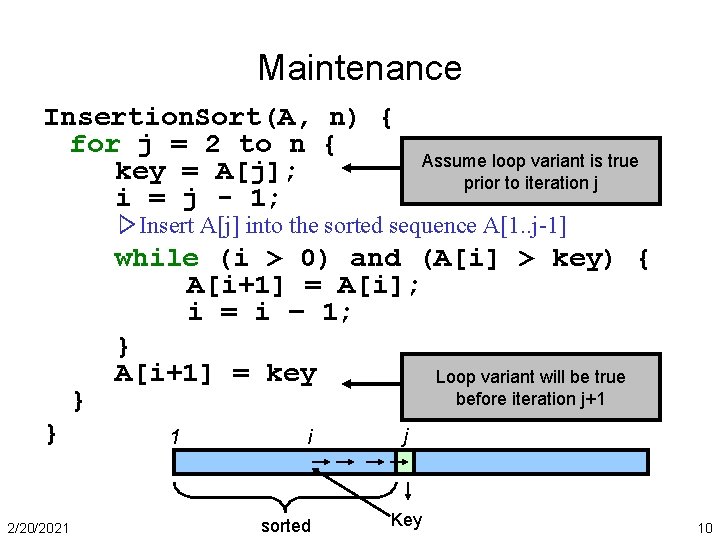
Maintenance Insertion. Sort(A, n) { for j = 2 to n { key = A[j]; i = j - 1; Assume loop variant is true prior to iteration j ▷Insert A[j] into the sorted sequence A[1. . j-1] } } 2/20/2021 while (i > 0) and (A[i] > key) { A[i+1] = A[i]; i = i – 1; } A[i+1] = key Loop variant will be true before iteration j+1 1 i sorted j Key 10

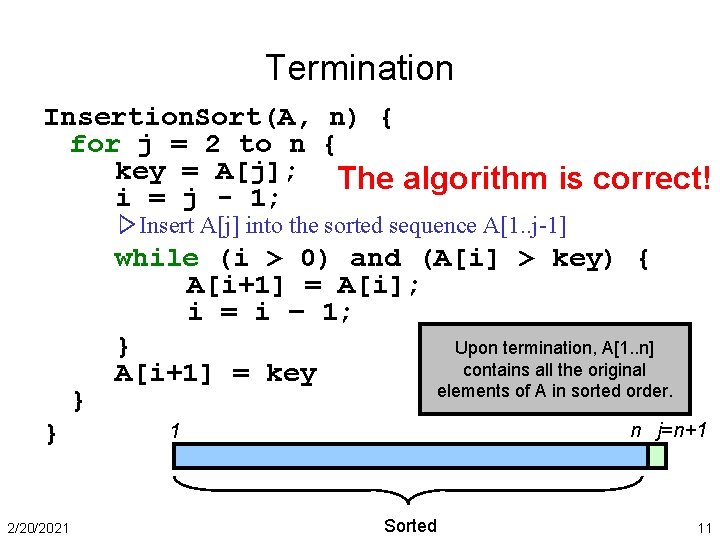
Termination Insertion. Sort(A, n) { for j = 2 to n { key = A[j]; The algorithm is correct! i = j - 1; ▷Insert A[j] into the sorted sequence A[1. . j-1] } } 2/20/2021 while (i > 0) and (A[i] > key) { A[i+1] = A[i]; i = i – 1; } Upon termination, A[1. . n] contains all the original A[i+1] = key elements of A in sorted order. n j=n+1 1 Sorted 11

Efficiency • Correctness alone is not sufficient – Brute-force algorithms exist for most problems – E. g. use permutation to sort – Problem: too slow! • How to measure efficiency? – Accurate running time is not a good measure – It depends on input, computer, and implementation, etc. 2/20/2021 12

Machine-independent • A generic uniprocessor random-access machine (RAM) model – No concurrent operations – Each simple operation (e. g. +, -, =, *, if, for) takes 1 step. • Loops and subroutine calls are not simple operations. – All memory equally expensive to access • Constant word size • Unless we are explicitly manipulating bits 2/20/2021 13

Analysis of insertion Sort Insertion. Sort(A, n) { for j = 2 to n { key = A[j] i = j - 1; while (i > 0) and (A[i] > key) { A[i+1] = A[i] i = i - 1 } A[i+1] = key } How many times will this line execute? } 2/20/2021 14

Analysis of insertion Sort Insertion. Sort(A, n) { for j = 2 to n { key = A[j] i = j - 1; while (i > 0) and (A[i] > key) { A[i+1] = A[i] i = i - 1 } A[i+1] = key } How many times will this line execute? } 2/20/2021 15

Analysis of insertion Sort Statement Insertion. Sort(A, n) { for j = 2 to n { key = A[j] i = j - 1; while (i > 0) and (A[i] > key) { A[i+1] = A[i] i = i - 1 } A[i+1] = key } } cost time__ c 1 c 2 c 3 c 4 c 5 c 6 0 c 7 0 n (n-1) S (S-(n-1)) (n-1) S = t 2 + t 3 + … + tn where tj is number of while th for loop iteration expression evaluations for the j 2/20/2021 16

Analyzing Insertion Sort • T(n) = c 1 n + c 2(n-1) + c 3(n-1) + c 4 S + c 5(S - (n-1)) + c 6(S - (n-1)) + c 7(n-1) = c 8 S + c 9 n + c 10 • What can S be? – Best case -- inner loop body never executed • tj = 1 S = n - 1 • T(n) = an + b is a linear function Θ (n) – Worst case -- inner loop body executed for all previous elements • tj = j S = 2 + 3 + … + n = n(n+1)/2 - 1 • T(n) = an 2 + bn + c is a quadratic function Θ (n 2) – Average case • Can assume that on average, we have to insert A[j] into the middle of A[1. . j-1], so tj = j/2 • S ≈ n(n+1)/4 Θ (n 2) • T(n) is still a quadratic function 2/20/2021 17

Analysis of insertion Sort Statement cost time__ Insertion. Sort(A, n) { for j = 2 to n { key = A[j] i = j - 1; while (i > 0) and (A[i] > key) { A[i+1] = A[i] i = i - 1 } A[i+1] = key } } c 1 c 2 c 3 c 4 c 5 c 6 0 c 7 0 n (n-1) S (S-(n-1)) (n-1) What are the basic operations (most executed lines)? 2/20/2021 18

Analysis of insertion Sort Statement Insertion. Sort(A, n) { for j = 2 to n { key = A[j] i = j - 1; while (i > 0) and (A[i] > key) { A[i+1] = A[i] i = i - 1 } A[i+1] = key } } 2/20/2021 cost time__ c 1 c 2 c 3 c 4 c 5 c 6 0 c 7 0 n (n-1) S (S-(n-1)) (n-1) 19

Analysis of insertion Sort Statement Insertion. Sort(A, n) { for j = 2 to n { key = A[j] i = j - 1; while (i > 0) and (A[i] > key) { A[i+1] = A[i] i = i - 1 } A[i+1] = key } } 2/20/2021 cost time__ c 1 c 2 c 3 c 4 c 5 c 6 0 c 7 0 n (n-1) S (S-(n-1)) (n-1) 20
![What can S be Inner loop stops when Ai key or i What can S be? Inner loop stops when A[i] <= key, or i =](https://slidetodoc.com/presentation_image_h/04e6a62291833cf2e25209601efcba47/image-21.jpg)
What can S be? Inner loop stops when A[i] <= key, or i = 0 i 1 sorted • • 2/20/2021 j Key S = j=2. . n tj Best case: Worst case: Average case: 21
![Best case Inner loop stops when Ai key or i 0 i Best case Inner loop stops when A[i] <= key, or i = 0 i](https://slidetodoc.com/presentation_image_h/04e6a62291833cf2e25209601efcba47/image-22.jpg)
Best case Inner loop stops when A[i] <= key, or i = 0 i j 1 sorted • • 2/20/2021 Key Array already sorted S = j=2. . n tj tj = 1 for all j S = n-1 T(n) = Θ (n) 22
![Worst case Inner loop stops when Ai key i j 1 sorted Worst case Inner loop stops when A[i] <= key i j 1 sorted •](https://slidetodoc.com/presentation_image_h/04e6a62291833cf2e25209601efcba47/image-23.jpg)
Worst case Inner loop stops when A[i] <= key i j 1 sorted • • 2/20/2021 Key Array originally in reverse order sorted S = j=2. . n tj tj = j S = j=2. . n j = 2 + 3 + … + n = (n-1) (n+2) / 2 = Θ (n 2) 23
![Average case Inner loop stops when Ai key i j 1 sorted Average case Inner loop stops when A[i] <= key i j 1 sorted •](https://slidetodoc.com/presentation_image_h/04e6a62291833cf2e25209601efcba47/image-24.jpg)
Average case Inner loop stops when A[i] <= key i j 1 sorted • • Key Array in random order S = j=2. . n tj tj = j / 2 on average S = j=2. . n j/2 = ½ j=2. . n j = (n-1) (n+2) / 4 = Θ (n 2) What if we use binary search? 2/20/2021 Answer: still Θ(n 2) 24

Asymptotic Analysis • Running time depends on the size of the input – Larger array takes more time to sort – T(n): the time taken on input with size n – Look at growth of T(n) as n→∞. “Asymptotic Analysis” • Size of input is generally defined as the number of input elements – In some cases may be tricky 2/20/2021 25

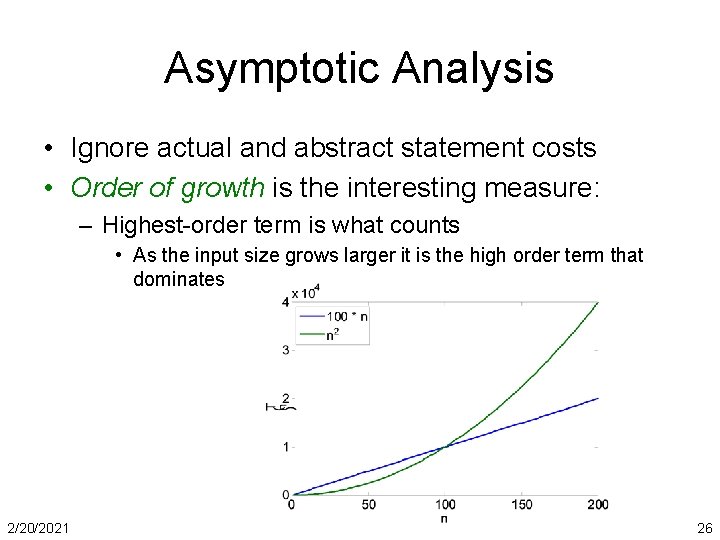
Asymptotic Analysis • Ignore actual and abstract statement costs • Order of growth is the interesting measure: – Highest-order term is what counts • As the input size grows larger it is the high order term that dominates 2/20/2021 26

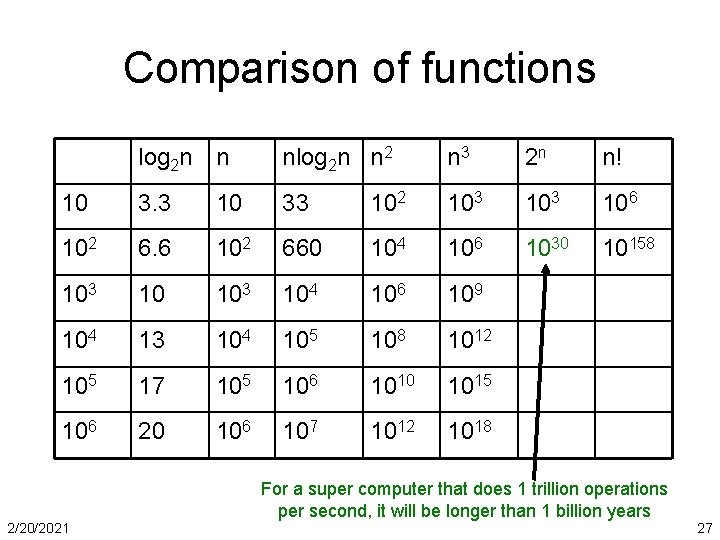
Comparison of functions log 2 n n nlog 2 n n 2 n 3 2 n n! 10 3. 3 10 33 102 103 106 102 660 104 106 1030 10158 103 104 106 109 104 13 104 105 108 1012 105 17 105 106 1010 1015 106 20 106 107 1012 1018 For a super computer that does 1 trillion operations per second, it will be longer than 1 billion years 2/20/2021 27

Order of growth 1 << log 2 n << nlog 2 n << n 2 << n 3 << 2 n << n! (We are slightly abusing of the “<<“ sign. It means a smaller order of growth). 2/20/2021 28

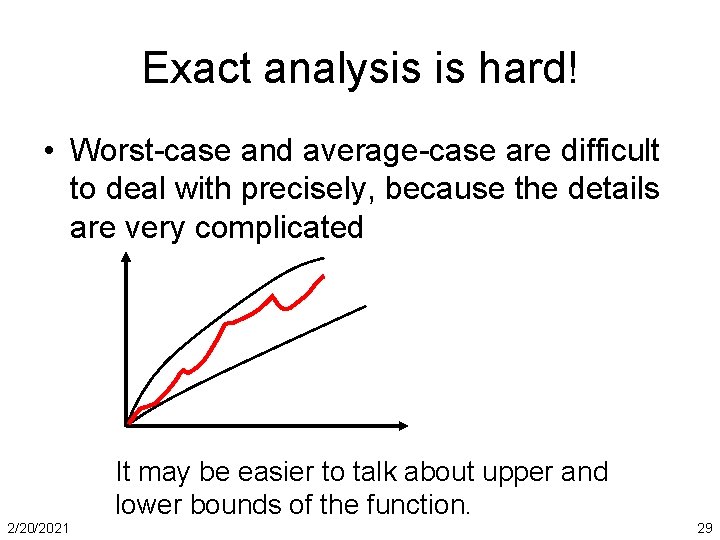
Exact analysis is hard! • Worst-case and average-case are difficult to deal with precisely, because the details are very complicated It may be easier to talk about upper and lower bounds of the function. 2/20/2021 29

Asymptotic notations • • • 2/20/2021 O: Big-Oh Ω: Big-Omega Θ: Theta o: Small-oh ω: Small-omega 30

Big O • Informally, O (g(n)) is the set of all functions with a smaller or same order of growth as g(n), within a constant multiple • If we say f(n) is in O(g(n)), it means that g(n) is an asymptotic upper bound of f(n) – Intuitively, it is like f(n) ≤ g(n) • What is O(n 2)? – The set of all functions that grow slower than or in the same order as n 2 2/20/2021 31

So: n O(n 2) n 2 O(n 2) 1000 n O(n 2) n 2 + n O(n 2) 100 n 2 + n O(n 2) Intuitively, O is like ≤ But: 1/1000 n 3 O(n 2) 2/20/2021 32

small o • Informally, o (g(n)) is the set of all functions with a strictly smaller growth as g(n), within a constant multiple • What is o(n 2)? – The set of all functions that grow slower than n 2 So: 1000 n o(n 2) But: Intuitively, o is like < n 2 o(n 2) 2/20/2021 33

Big Ω • Informally, Ω (g(n)) is the set of all functions with a larger or same order of growth as g(n), within a constant multiple • f(n) Ω(g(n)) means g(n) is an asymptotic lower bound of f(n) – Intuitively, it is like g(n) ≤ f(n) So: Ω(n) 1/1000 n 2 Ω(n) n 2 Intuitively, Ω is like ≥ But: 1000 n Ω(n 2) 2/20/2021 34

small ω • Informally, ω (g(n)) is the set of all functions with a larger order of growth as g(n), within a constant multiple So: n 2 ω(n) 1/1000 n 2 ω(n) n 2 ω(n 2) 2/20/2021 Intuitively, ω is like > 35

Theta (Θ) • Informally, Θ (g(n)) is the set of all functions with the same order of growth as g(n), within a constant multiple • f(n) Θ(g(n)) means g(n) is an asymptotically tight bound of f(n) – Intuitively, it is like f(n) = g(n) • What is Θ(n 2)? – The set of all functions that grow in the same order as n 2 2/20/2021 36

So: n 2 Θ(n 2) n 2 + n Θ(n 2) 100 n 2 + log 2 n Θ(n 2) Intuitively, Θ is like = But: nlog 2 n Θ(n 2) 1000 n Θ(n 2) 1/1000 n 3 Θ(n 2) 2/20/2021 37

Tricky cases • How about sqrt(n) and log 2 n? • How about log 2 n and log 10 n • How about 2 n and 3 n • How about 3 n and n!? 2/20/2021 38

Big-Oh • Definition: There exist For all O(g(n)) = {f(n): positive constants c and n 0 such that 0 ≤ f(n) ≤ cg(n) n>n 0} • lim n→∞ g(n)/f(n) > 0 (if the limit exists. ) • Abuse of notation (for convenience): f(n) = O(g(n)) actually means f(n) O(g(n)) 2/20/2021 39

Big-Oh • Claim: f(n) = 3 n 2 + 10 n + 5 O(n 2) • Proof by definition (Hint: to prove this claim by definition, we need to find some positive constants c and n 0 such that f(n) <= cn 2 for all n > n 0. ) (Note: you just need to find one concrete example of c and n 0 satisfying the condition, but it needs to be correct for all n > n 0. So do not try to plug in a concrete value of n and show the inequality holds. ) Proof: 3 n 2 + 10 n + 5 3 n 2 + 10 n 2 + 5, n > 1 3 n 2 + 10 n 2 + 5 n 2, n > 1 18 n 2, n > 1 If we let c = 30 and n 0 = 1, we have f(n) c n 2, n > n 0. Therefore by definition, f(n) = O(n 2). 2/20/2021 40

Big-Omega • Definition: Ω(g(n)) = {f(n): positive constants c and n 0 such that 0 ≤ cg(n) ≤ f(n) n>n 0} • lim n→∞ f(n)/g(n) > 0 (if the limit exists. ) • Abuse of notation (for convenience): f(n) = Ω(g(n)) actually means f(n) Ω(g(n)) 2/20/2021 41

Big-Omega • Claim: f(n) = n 2 / 10 = Ω(n) • Proof by definition: f(n) = n 2 / 10, g(n) = n Need to find a c and a no to satisfy the definition of f(n) Ω(g(n)), i. e. , f(n) ≥ cg(n) for n > n 0 Proof: n ≤ n 2 / 10 when n ≥ 10 If we let c = 1 and n 0 = 10, we have f(n) ≥ cn, n > n 0. Therefore, by definition, n 2 / 10 = Ω(n). 2/20/2021 42

Theta • Definition: – Θ(g(n)) = {f(n): positive constants c 1, c 2, and n 0 such that 0 c 1 g(n) f(n) c 2 g(n), n n 0 } • f(n) = O(g(n)) and f(n) = Ω(g(n)) • Abuse of notation (for convenience): f(n) = Θ(g(n)) actually means f(n) Θ(g(n)) Θ(1) means constant time. 2/20/2021 43

Theta • Claim: f(n) = 2 n 2 + n = Θ (n 2) • Proof by definition: – Need to find the three constants c 1, c 2, and n 0 such that c 1 n 2 ≤ 2 n 2+n ≤ c 2 n 2 for all n > n 0 – A simple solution is c 1 = 2, c 2 = 3, and n 0 = 1 2/20/2021 44

More Examples • Prove n 2 + 3 n + lg n is in O(n 2) • Need to find c and n 0 such that n 2 + 3 n + lg n <= cn 2 for n > n 0 • Proof: n 2 + 3 n + lg n <= n 2 + 3 n 2 + n 2 <= 5 n 2 for n > 1 Therefore by definition n 2 + 3 n + lg n O(n 2). (Alternatively: n 2 + 3 n + lg n <= n 2 + n 2 for n > 10 <= 3 n 2 for n > 10) 2/20/2021 45

More Examples • Prove n 2 + 3 n + lg n is in Ω(n 2) • Want to find c and n 0 such that n 2 + 3 n + lg n >= cn 2 for n > n 0 n 2 + 3 n + lg n >= n 2 for n > 0 n 2 + 3 n + lg n = O(n 2) and n 2 + 3 n + lg n = Ω (n 2) => n 2 + 3 n + lg n = Θ(n 2) 2/20/2021 46

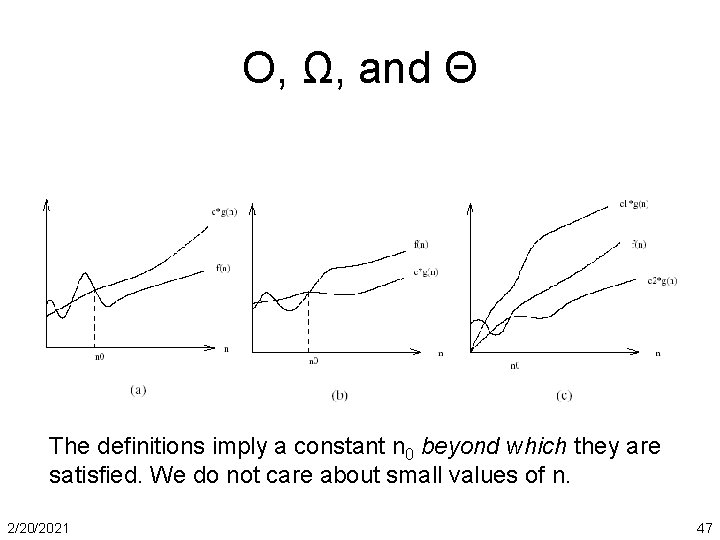
O, Ω, and Θ The definitions imply a constant n 0 beyond which they are satisfied. We do not care about small values of n. 2/20/2021 47

Using limits to compare orders of growth f(n) o(g(n)) • lim f(n) / g(n) = n→∞ 0 c >0 ∞ f(n) O(g(n)) f(n) Θ (g(n)) f(n) Ω(g(n)) f(n) ω (g(n)) 2/20/2021 48

logarithms • compare log 2 n and log 10 n • • 2/20/2021 logab = logcb / logca log 2 n = log 10 n / log 102 ~ 3. 3 log 10 n Therefore lim(log 2 n / log 10 n) = 3. 3 log 2 n = Θ (log 10 n) 49

• Compare 2 n and 3 n n / 3 n = lim(2/3)n = 0 • lim 2 n→∞ • Therefore, 2 n o(3 n), and 3 n ω(2 n) • How about 2 n and 2 n+1? 2 n / 2 n+1 = ½, therefore 2 n = Θ (2 n+1) 2/20/2021 50

L’ Hopital’s rule lim f(n) / g(n) = lim f(n)’ / g(n)’ n→∞ Condition: If both lim f(n) and lim g(n) are or 0 • You can apply this transformation as many times as you want, as long as the condition holds 2/20/2021 51

• Compare n 0. 5 and log n • lim n 0. 5 / log n = ? n→∞ • • • 2/20/2021 (n 0. 5)’ = 0. 5 n-0. 5 (log n)’ = 1 / n lim (n-0. 5 / 1/n) = lim(n 0. 5) = ∞ Therefore, log n o(n 0. 5) In fact, log n o(nε), for any ε > 0 52

Stirling’s formula (constant) 2/20/2021 53
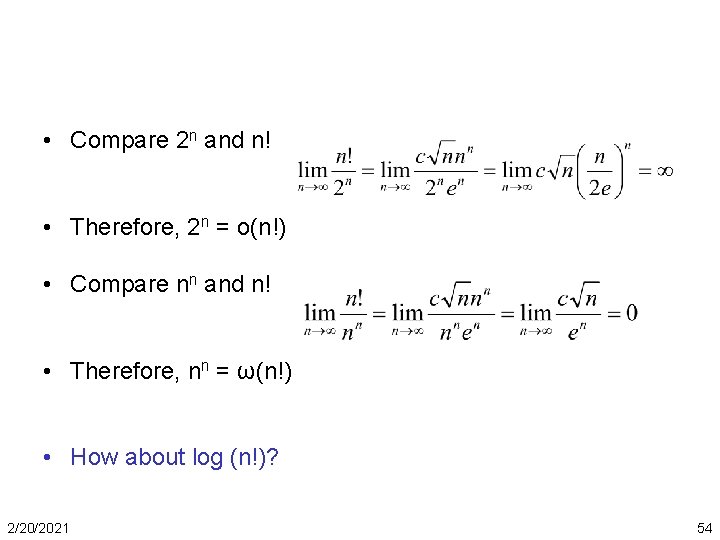
• Compare 2 n and n! • Therefore, 2 n = o(n!) • Compare nn and n! • Therefore, nn = ω(n!) • How about log (n!)? 2/20/2021 54
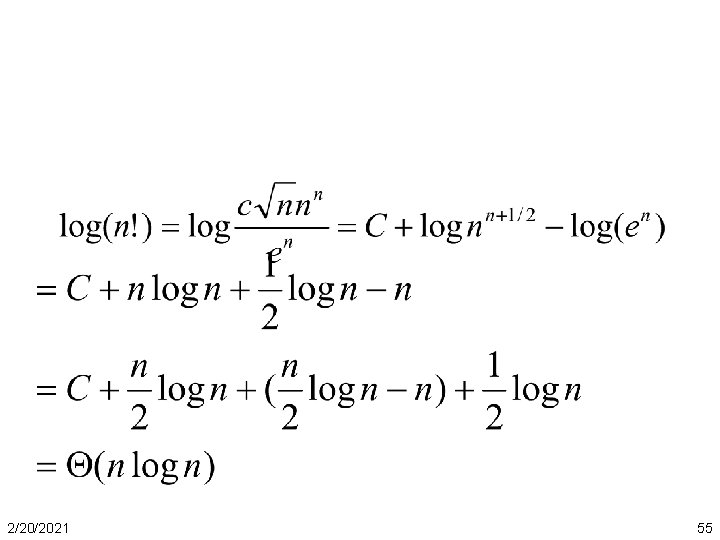
2/20/2021 55

More advanced dominance ranking 2/20/2021 56

Asymptotic notations • • • O: Big-Oh Ω: Big-Omega Θ: Theta o: Small-oh ω: Small-omega Intuitively: O is like o is like < 2/20/2021 is like > is like = 57