CS 3343 Analysis of Algorithms Lecture 26 String

CS 3343: Analysis of Algorithms Lecture 26: String Matching Algorithms

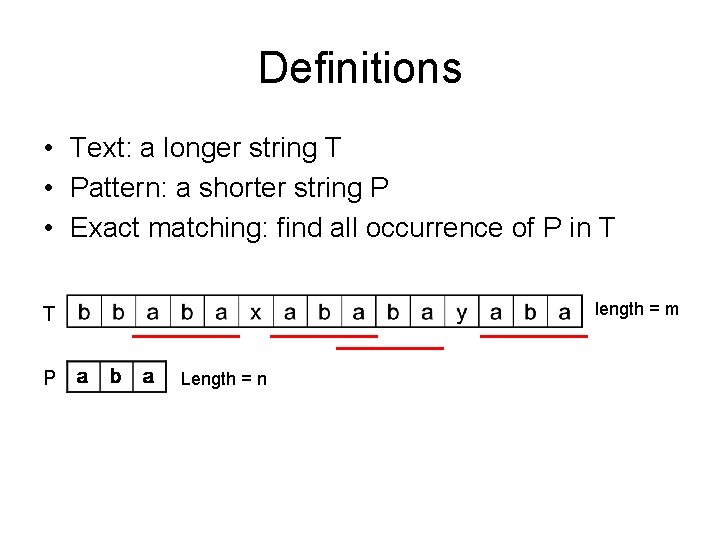
Definitions • Text: a longer string T • Pattern: a shorter string P • Exact matching: find all occurrence of P in T length = m T P Length = n

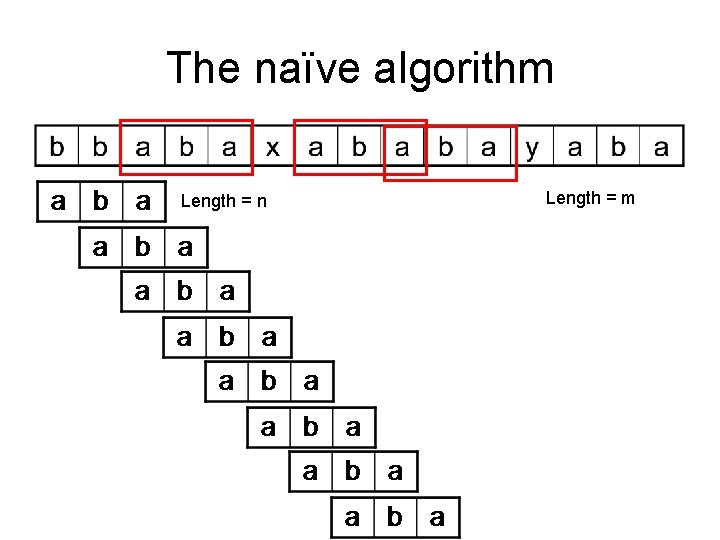
The naïve algorithm Length = n Length = m

Time complexity • Worst case: O(mn) • Best case: O(m) – aaaaaaa vs. baaaaaaa • Average case? – Alphabet size = k – Assume equal probability – How many chars do you need to compare before find a mismatch? • In average: k / (k-1) • Therefore average-case complexity: mk / (k-1) • For large alphabet, ~ m – Not as bad as you thought, huh?

Real strings are not random T: aaaaaaaaaaaaa P: aaaab Plus: O(m) average case is still bad for long strings! Smarter algorithms: O(m + n) in worst case sub-linear in practice how is this possible?

How to speedup? • Pre-processing T or P • Why pre-processing can save us time? – Uncovers the structure of T or P – Determines when we can skip ahead without missing anything – Determines when we can infer the result of character comparisons without actually doing them. ACGTAXACXTAXACGXAX ACGTACA

Cost for exact string matching Overhead Total cost = cost (preprocessing) + cost(comparison) + cost(output) Constant Hope: gain > overhead Minimize

String matching scenarios • One T and one P – Search a word in a document • One T and many P all at once – Search a set of words in a document – Spell checking • One fixed T, many P – Search a completed genome for a short sequence • Two (or many) T’s for common patterns • Would you preprocess P or T? • Always pre-process the shorter seq, or the one that is repeatedly used

Pattern pre-processing algs – Karp – Rabin algorithm • Small alphabet and small pattern – Boyer – Moore algorithm • The choice of most cases • Typically sub-linear time – Knuth-Morris-Pratt algorithm (KMP) – Aho-Corasick algorithm • The algorithm for the unix utility fgrep – Suffix tree • One of the most useful preprocessing techniques • Many applications

Algorithm KMP • Not the fastest • Best known • Good for “real-time matching” – i. e. text comes one char at a time – No memory of previous chars • Idea – Left-to-right comparison – Shift P more than one char whenever possible

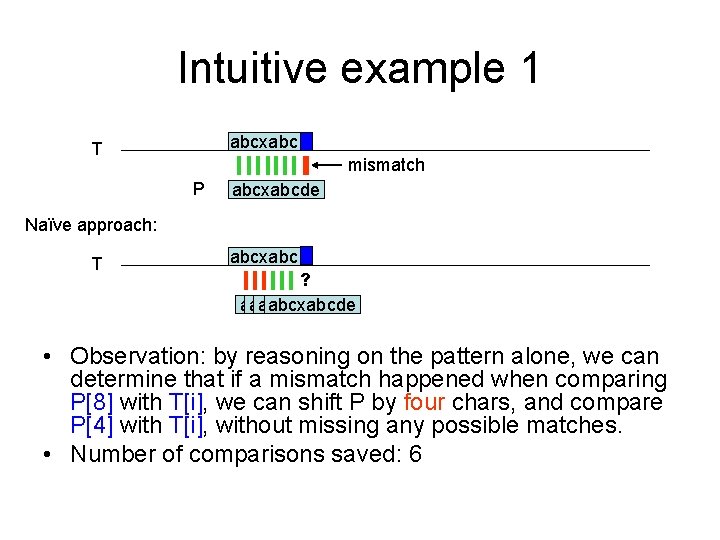
Intuitive example 1 abcxabc T mismatch P abcxabcde Naïve approach: T abcxabc ? abcxabcde • Observation: by reasoning on the pattern alone, we can determine that if a mismatch happened when comparing P[8] with T[i], we can shift P by four chars, and compare P[4] with T[i], without missing any possible matches. • Number of comparisons saved: 6

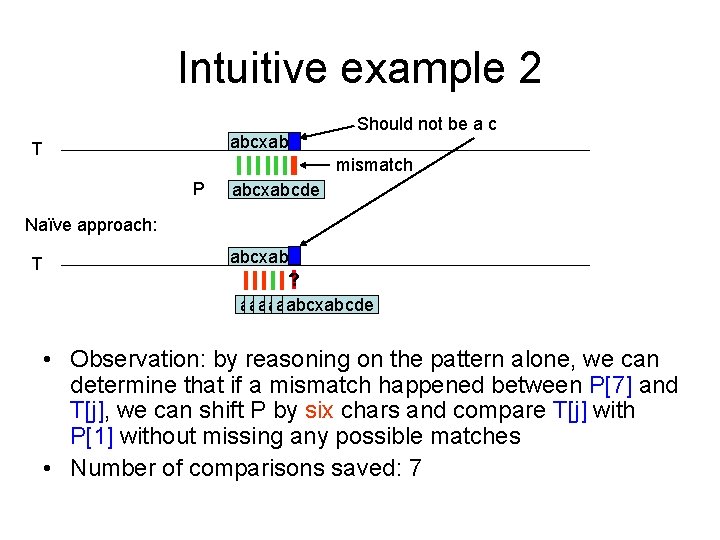
Intuitive example 2 abcxabc T Should not be a c mismatch P abcxabcde Naïve approach: T abcxabc ? abcxabcde abcxabcde • Observation: by reasoning on the pattern alone, we can determine that if a mismatch happened between P[7] and T[j], we can shift P by six chars and compare T[j] with P[1] without missing any possible matches • Number of comparisons saved: 7

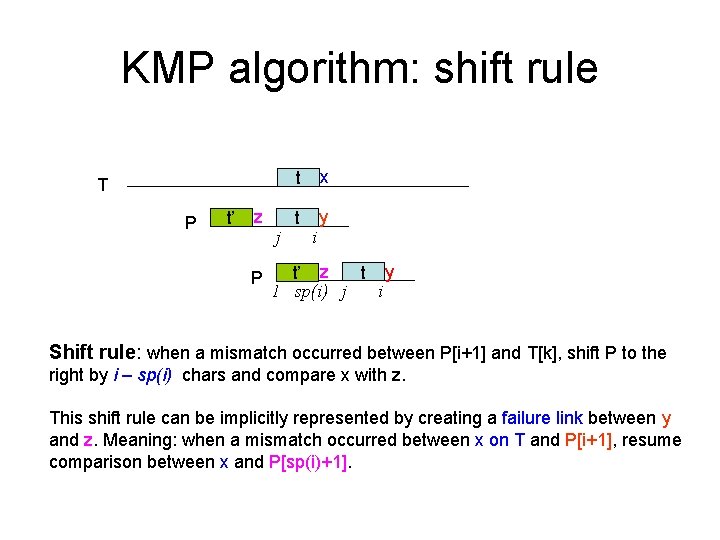
KMP algorithm: pre-processing • Key: the reasoning is done without even knowing what string T is. • Only the location of mismatch in P must be known. T P t’ z P j t x t y t’ i z j t i y Pre-processing: for any position i in P, find P[1. . i]’s longest proper suffix, t = P[j. . i], such that t matches to a prefix of P, t’, and the next char of t is different from the next char of t’ (i. e. , y ≠ z) For each i, let sp(i) = length(t)

KMP algorithm: shift rule T P t’ z P j t x t y i t y t’ z 1 sp(i) j i Shift rule: when a mismatch occurred between P[i+1] and T[k], shift P to the right by i – sp(i) chars and compare x with z. This shift rule can be implicitly represented by creating a failure link between y and z. Meaning: when a mismatch occurred between x on T and P[i+1], resume comparison between x and P[sp(i)+1].

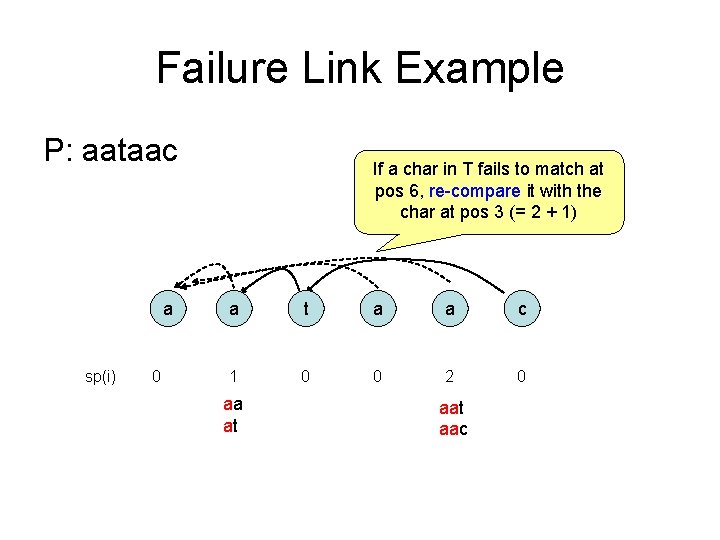
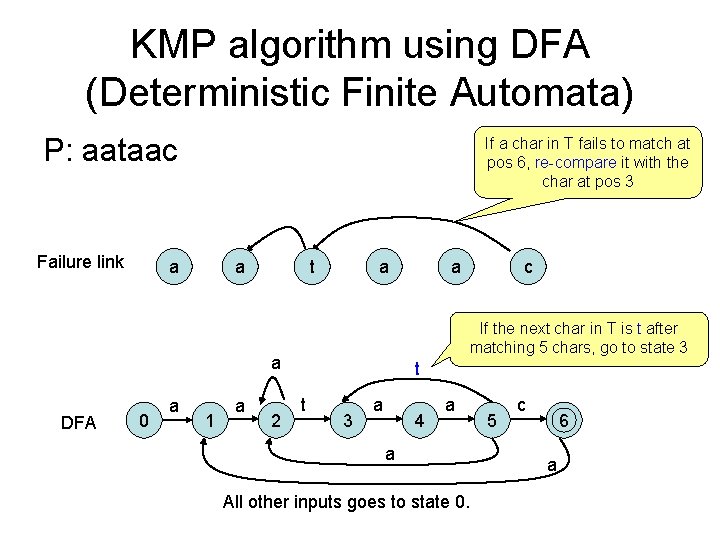
Failure Link Example P: aataac a sp(i) 0 If a char in T fails to match at pos 6, re-compare it with the char at pos 3 (= 2 + 1) a t a a c 1 0 0 2 0 aa at aac

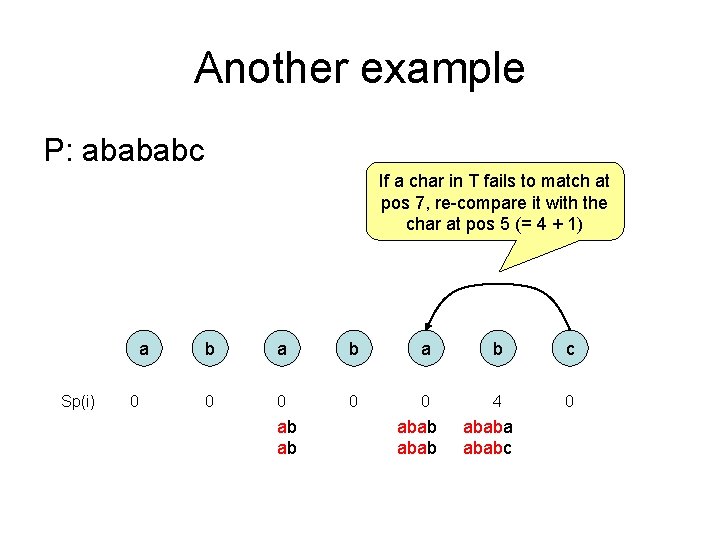
Another example P: abababc If a char in T fails to match at pos 7, re-compare it with the char at pos 5 (= 4 + 1) a Sp(i) 0 b a b c 0 0 4 0 ab ab ababa ababc

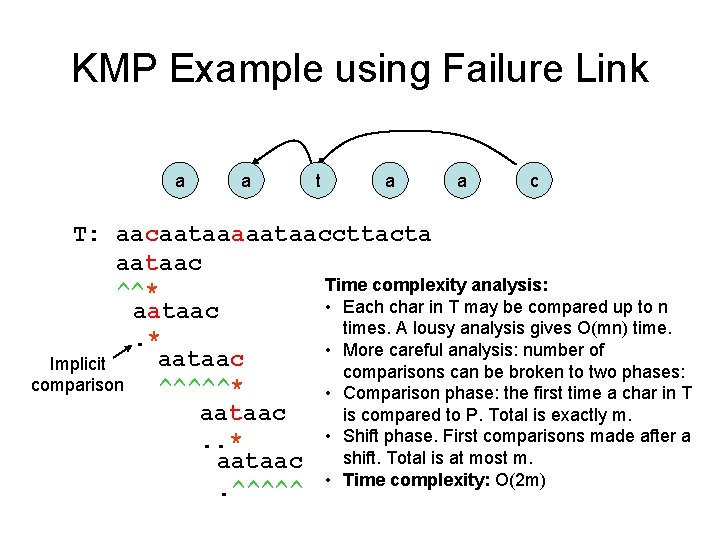
KMP Example using Failure Link a a t a a c T: aacaataaaaataaccttacta aataac Time complexity analysis: ^^* • Each char in T may be compared up to n aataac times. A lousy analysis gives O(mn) time. . * • More careful analysis: number of aataac Implicit comparisons can be broken to two phases: comparison ^^^^^* • Comparison phase: the first time a char in T aataac is compared to P. Total is exactly m. • Shift phase. First comparisons made after a. . * shift. Total is at most m. aataac. ^^^^^ • Time complexity: O(2 m)

KMP algorithm using DFA (Deterministic Finite Automata) P: aataac Failure link If a char in T fails to match at pos 6, re-compare it with the char at pos 3 a a t a DFA 0 1 a 2 c If the next char in T is t after matching 5 chars, go to state 3 a a a t t 3 a 4 a a All other inputs goes to state 0. 5 c 6 a

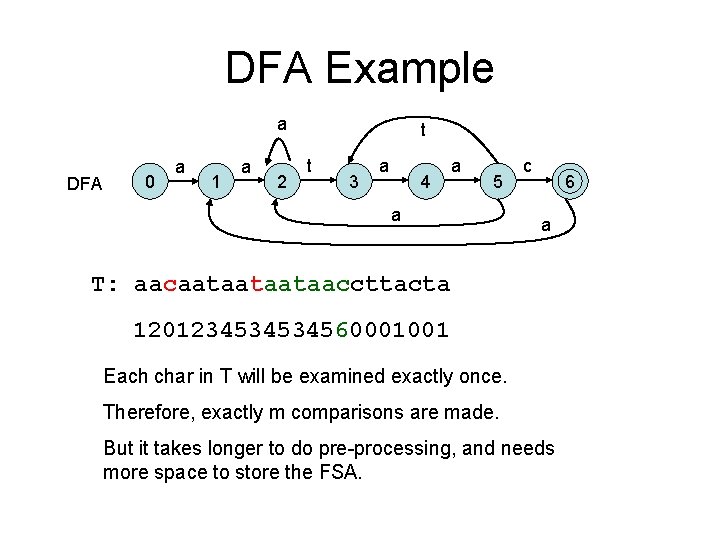
DFA Example a DFA 0 a 1 a 2 t t 3 a 4 a 5 a c 6 a T: aacaataataataaccttacta 1201234534534560001001 Each char in T will be examined exactly once. Therefore, exactly m comparisons are made. But it takes longer to do pre-processing, and needs more space to store the FSA.

Difference between Failure Link and DFA • Failure link – Preprocessing time and space are O(n), regardless of alphabet size – Comparison time is at most 2 m (at least m) • DFA – Preprocessing time and space are O(n | |) • May be a problem for very large alphabet size • For example, each “char” is a big integer • Chinese characters – Comparison time is always m.

The set matching problem • Find all occurrences of a set of patterns in T • First idea: run KMP or BM for each P – O(km + n) • k: number of patterns • m: length of text • n: total length of patterns • Better idea: combine all patterns together and search in one run

A simpler problem: spell-checking • A dictionary contains five words: – – – potato poetry pottery science school • Given a document, check if any word is (not) in the dictionary – Words in document are separated by special chars. – Relatively easy.

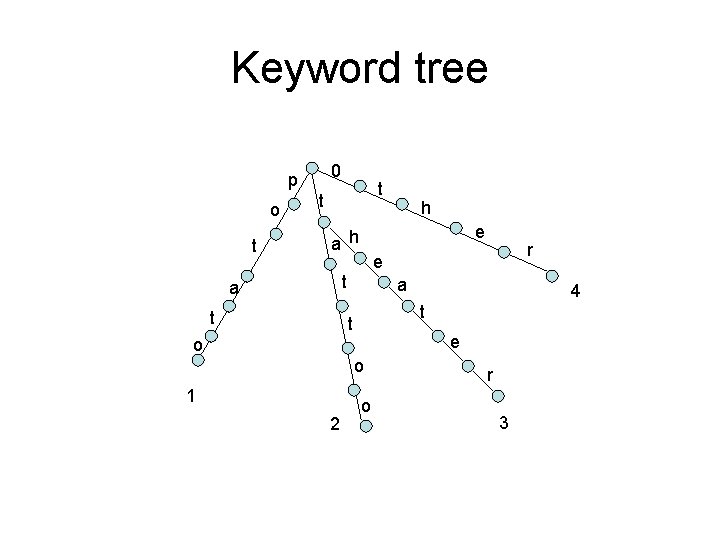
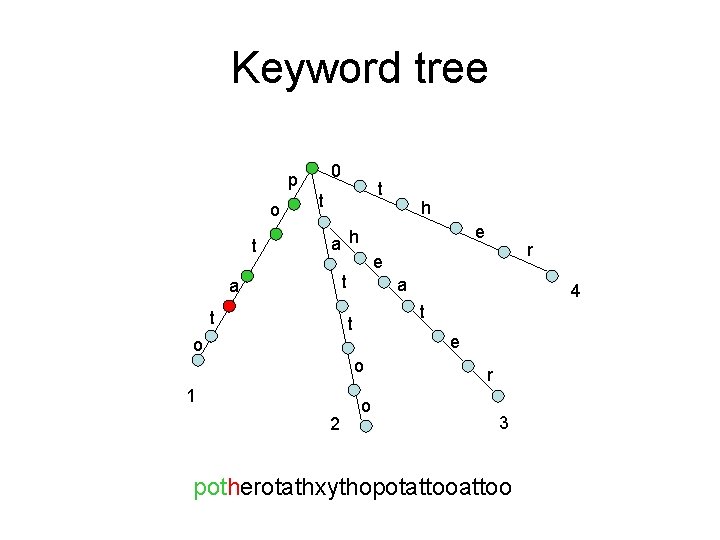
Keyword tree for spell checking This version of the potato gun was inspired by the Weird Science team out of Illinois p s o t o 1 o o l i e t t r e n y c r y 2 • • h e t a c 3 e 4 O(n) time to construct. n: total length of patterns. Search time: O(m). m: length of text Common prefix only need to be compared once. What if there is no space between words? 5

Aho-Corasick algorithm • Basis of the fgrep algorithm • Generalizing KMP – Using failure links • Example: given the following 4 patterns: – potato – tattoo – theater – other

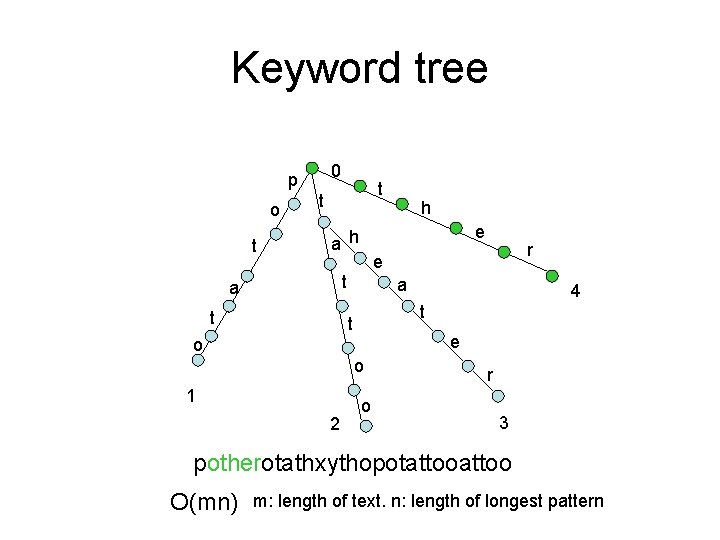
Keyword tree 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3

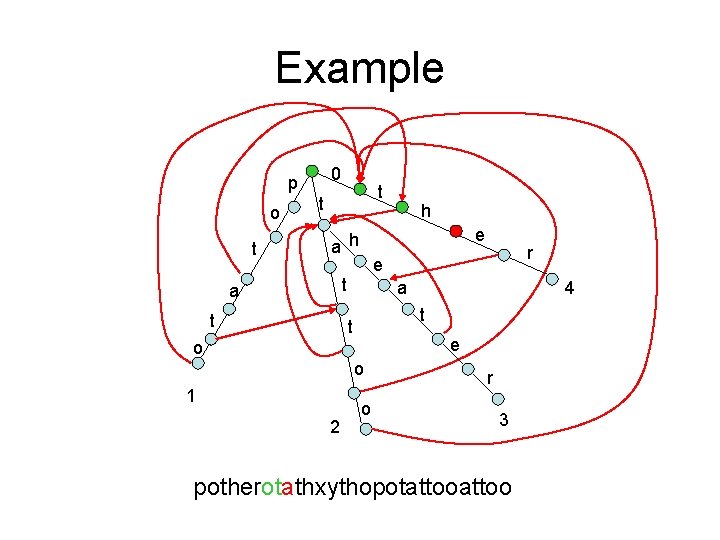
Keyword tree 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3 potherotathxythopotattoo

Keyword tree 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3 potherotathxythopotattoo O(mn) m: length of text. n: length of longest pattern

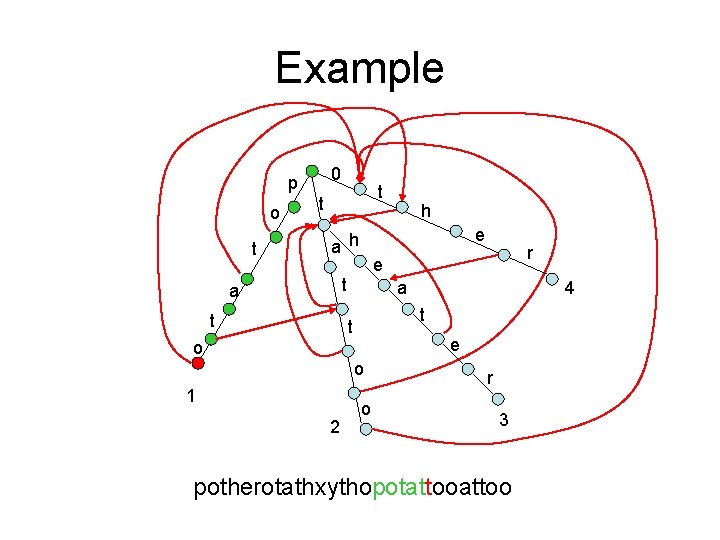
Keyword Tree with a failure link 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3 potherotathxythopotattoo

Keyword Tree with a failure link 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3 potherotathxythopotattoo

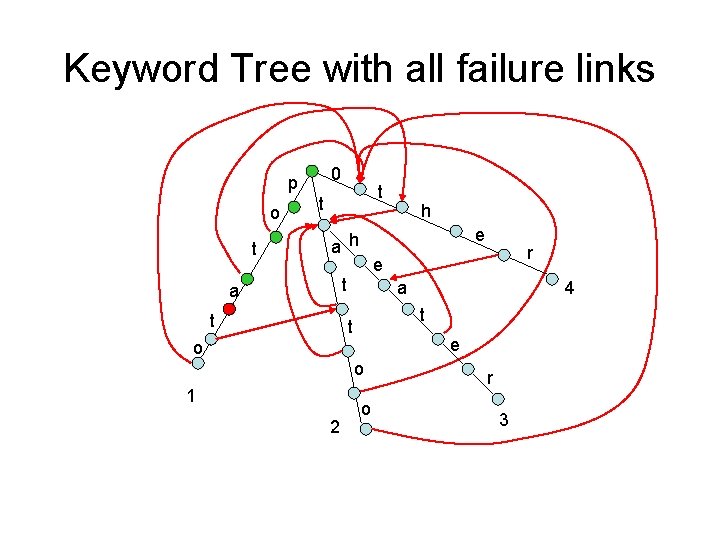
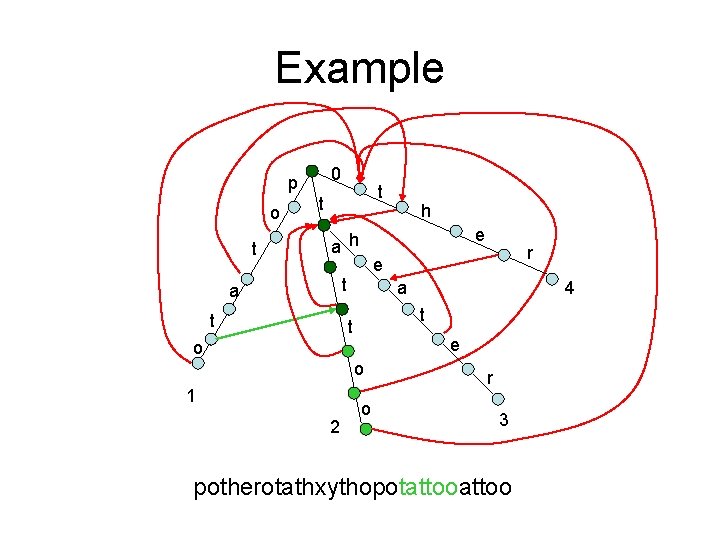
Keyword Tree with all failure links 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3

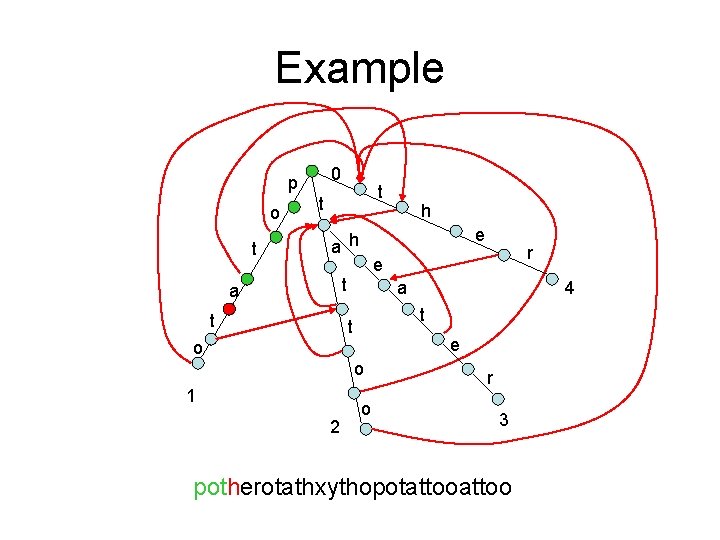
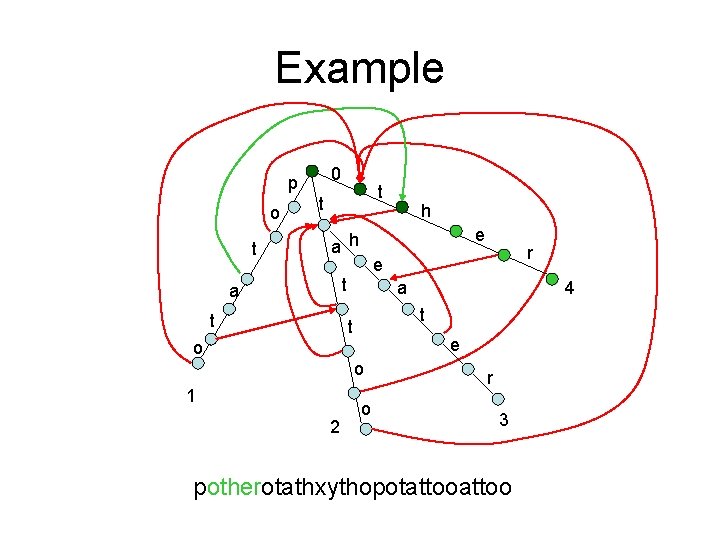
Example 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3 potherotathxythopotattoo

Example 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3 potherotathxythopotattoo

Example 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3 potherotathxythopotattoo

Example 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3 potherotathxythopotattoo

Example 0 p o t t t e a h t a e o o 2 4 t t 1 r e t a h o r 3 potherotathxythopotattoo

Aho-Corasick algorithm • O(n) preprocessing, and O(m+k) searching. – n: total length of patterns. – m: length of text – k is # of occurrence. • Can create a DFA similar as in KMP. – Requires more space, – Preprocessing time depends on alphabet size – Search time is constant

Suffix Tree • All algorithms we talked about so far preprocess pattern(s) – – Karp-Rabin: small pattern, small alphabet Boyer-Moore: fastest in practice. O(m) worst case. KMP: O(m) Aho-Corasick: O(m) • In some cases we may prefer to pre-process T – Fixed T, varying P • Suffix tree: basically a keyword tree of all suffixes

Suffix tree • • T: xabxac Suffixes: 1. 2. 3. 4. 5. 6. xabxac ac c a c 2 a x b c 5 b x a c 6 c b x a c 1 4 3 Naïve construction: O(m 2) using Aho-Corasick. Smarter: O(m). Very technical. big constant factor Difference from a keyword tree: create an internal node only when there is a branch

Suffix tree implementation • Explicitly labeling seq end • T: xabxa$ x a a a 2 x b b x a a 1 $ 3 x a 2 a x b $ 5 b x a $ 3 $ 4 b x a$ 1

Suffix tree implementation • Implicitly labeling edges • T: xabxa$ x a a $ 2 a x b $ 5 b x a $ b x a$ $ 3: $ 5 2 3: $ $ 3 2: 2 1 4 1: 2 3 4 1

Suffix links • Similar to failure link in a keyword tree • Only link internal nodes having branches x b g h j i f d e c a a b xabcf c d f e f g h i j

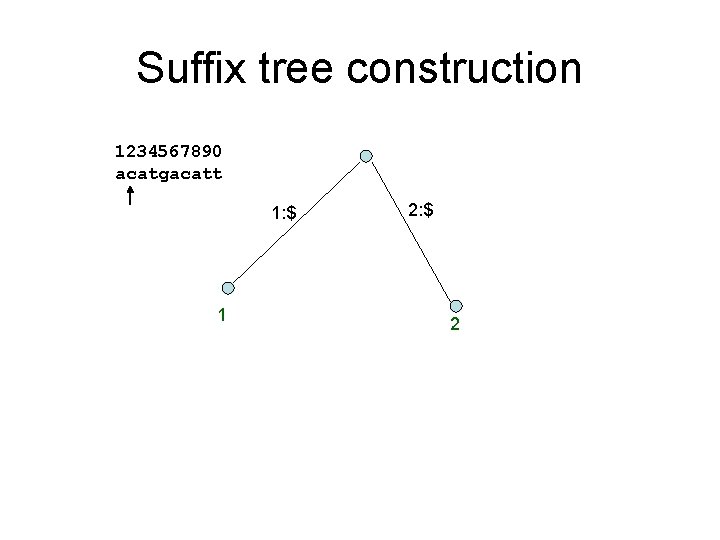
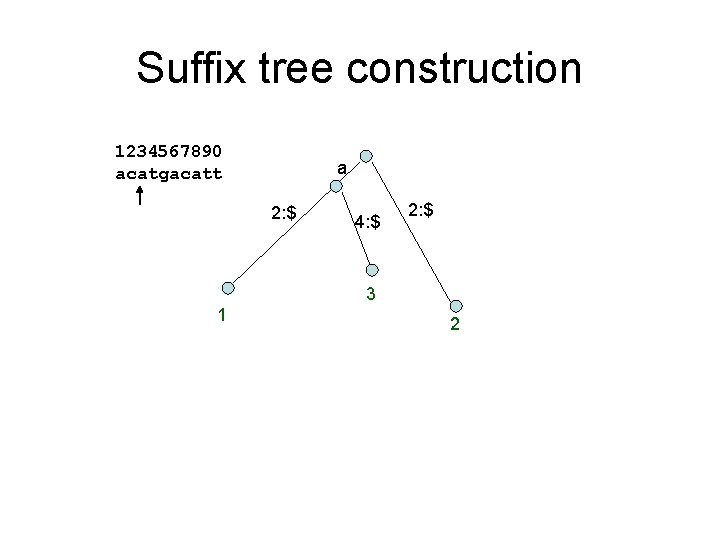
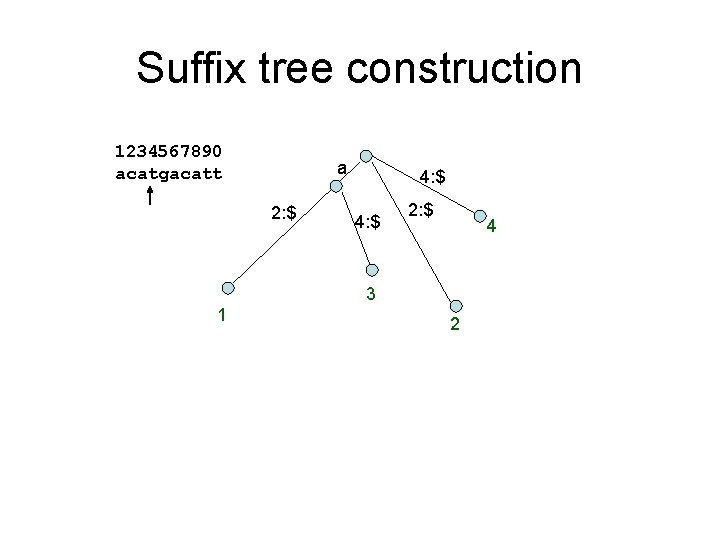
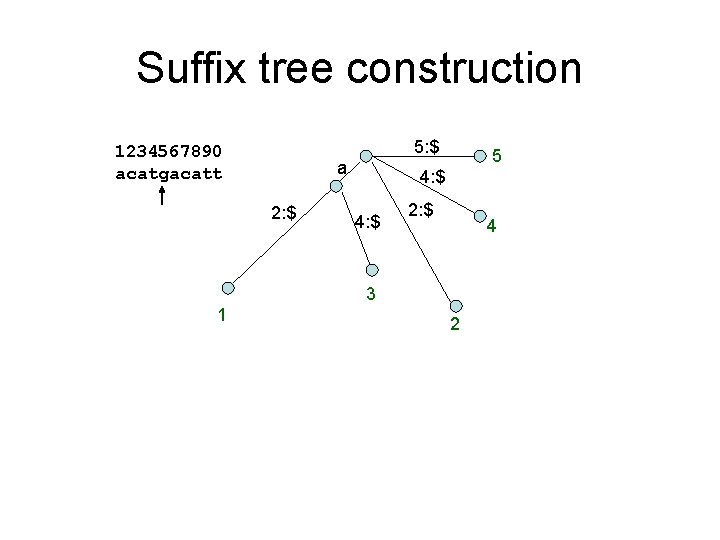
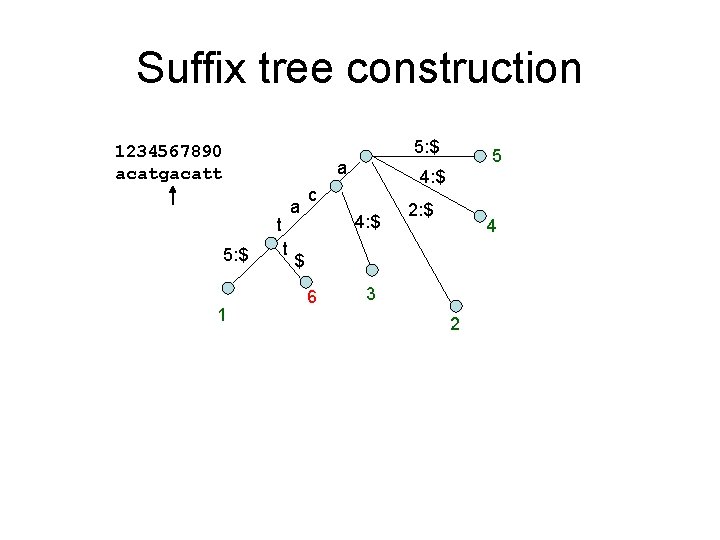
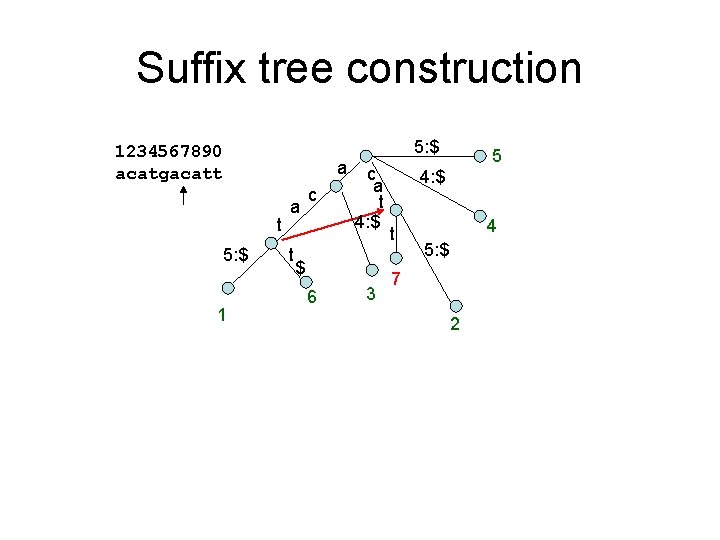
Suffix tree construction 1234567890 acatgacatt 1: $ 1

Suffix tree construction 1234567890 acatgacatt 1: $ 1 2: $ 2

Suffix tree construction 1234567890 acatgacatt a 2: $ 4: $ 2: $ 3 1 2

Suffix tree construction 1234567890 acatgacatt a 2: $ 4: $ 2: $ 4 3 1 2

Suffix tree construction 5: $ 1234567890 acatgacatt a 2: $ 5 4: $ 2: $ 4 3 1 2

Suffix tree construction 5: $ 1234567890 acatgacatt a a t 5: $ 1 t 5 4: $ c 4: $ 2: $ 4 $ 6 3 2

Suffix tree construction 5: $ 1234567890 acatgacatt a t 5: $ 1 a t c c a t 4: $ $ 6 3 5 4: $ t 4 5: $ 7 2

Suffix tree construction 5: $ 1234567890 acatgacatt a t 5: $ 1 a t c t $ 6 8 c a t t 5: $ 3 5 4: $ t 4 5: $ 7 2

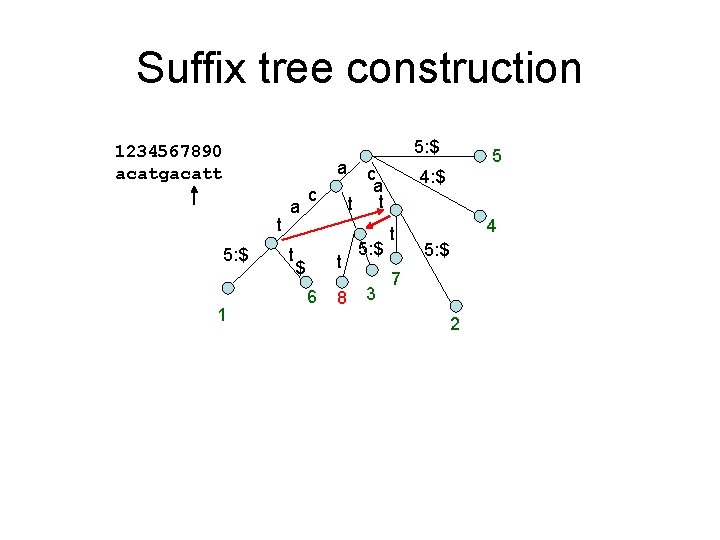
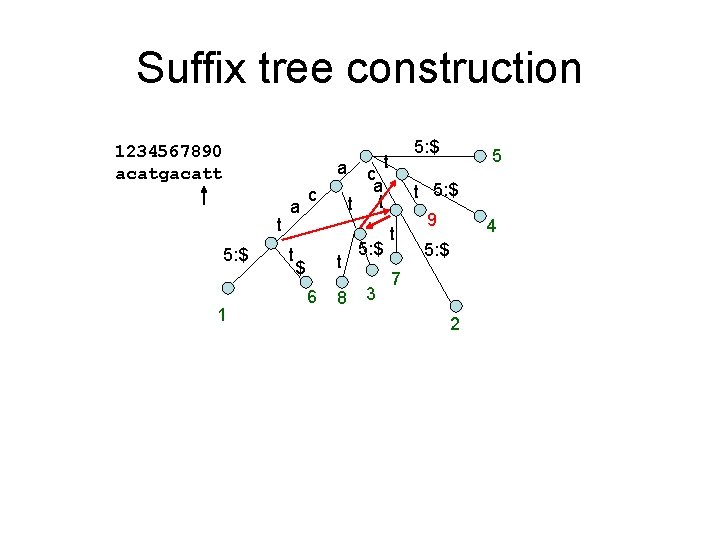
Suffix tree construction 1234567890 acatgacatt a t 5: $ 1 a t c t $ 6 8 5: $ t c a t t 5: $ 3 5 t 5: $ t 9 4 5: $ 7 2

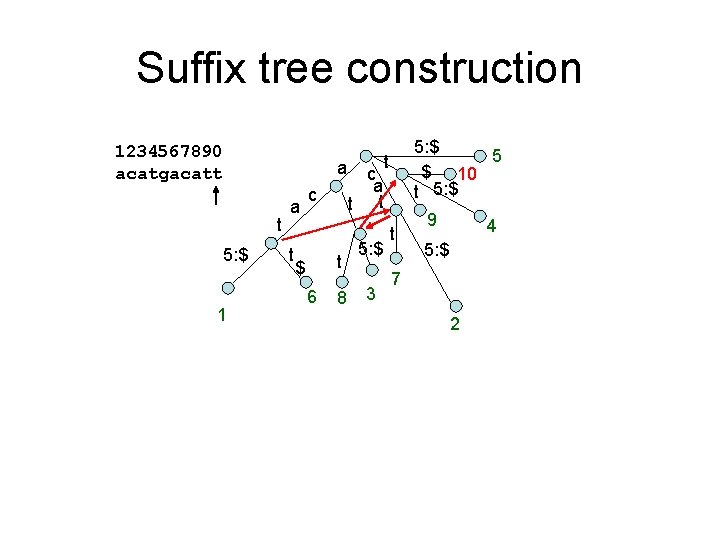
Suffix tree construction 1234567890 acatgacatt a t 5: $ 1 a t c t $ 6 8 5: $ 5 $ 10 t 5: $ t c a t t 5: $ 3 t 9 4 5: $ 7 2

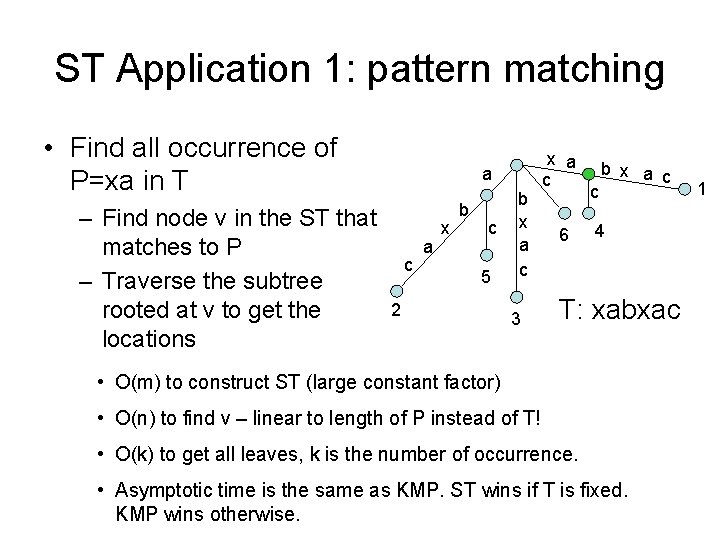
ST Application 1: pattern matching • Find all occurrence of P=xa in T – Find node v in the ST that matches to P – Traverse the subtree rooted at v to get the locations a c a x b c 5 2 b x a c 3 x a c 6 c b x a c 4 T: xabxac • O(m) to construct ST (large constant factor) • O(n) to find v – linear to length of P instead of T! • O(k) to get all leaves, k is the number of occurrence. • Asymptotic time is the same as KMP. ST wins if T is fixed. KMP wins otherwise. 1

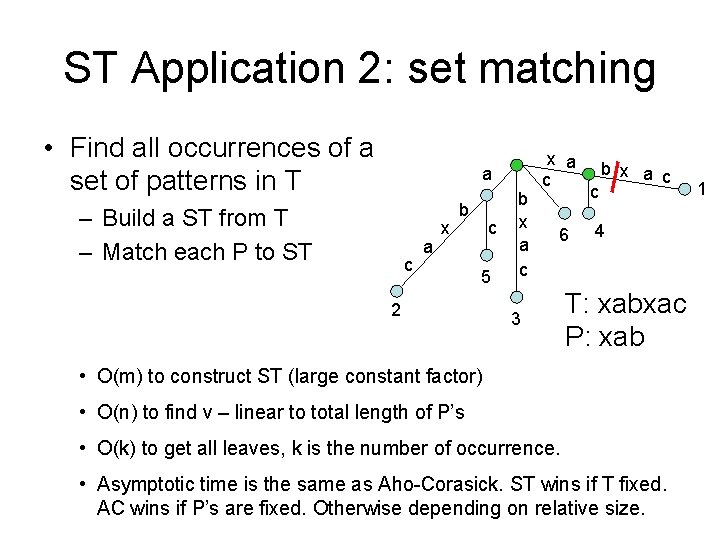
ST Application 2: set matching • Find all occurrences of a set of patterns in T a – Build a ST from T – Match each P to ST c a x b c 5 2 b x a c 6 3 c b x a c 4 T: xabxac P: xab • O(m) to construct ST (large constant factor) • O(n) to find v – linear to total length of P’s • O(k) to get all leaves, k is the number of occurrence. • Asymptotic time is the same as Aho-Corasick. ST wins if T fixed. AC wins if P’s are fixed. Otherwise depending on relative size. 1

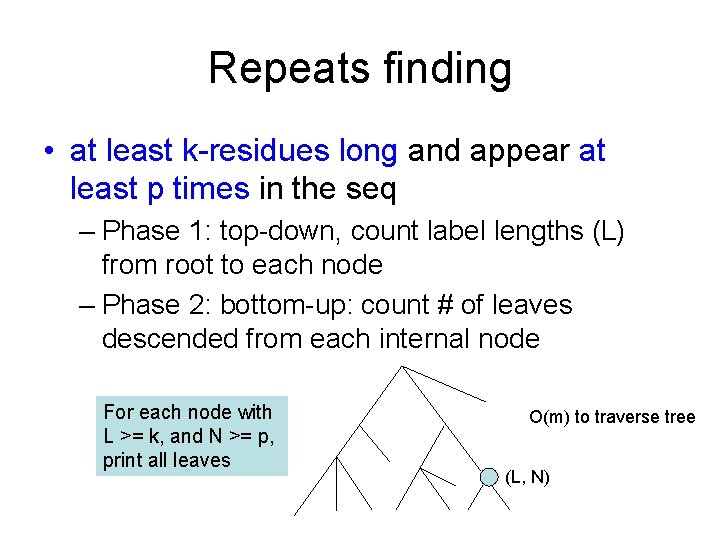
ST application 3: repeats finding • Genome contains many repeated DNA sequences • Repeat sequence length: Varies from 1 nucleotide to millions – Genes may have multiple copies (50 to 10, 000) – Highly repetitive DNA in some non-coding regions • 6 to 10 bp x 100, 000 to 1, 000 times • Problem: find all repeats that are at least kresidues long and appear at least p times in the genome

Repeats finding • at least k-residues long and appear at least p times in the seq – Phase 1: top-down, count label lengths (L) from root to each node – Phase 2: bottom-up: count # of leaves descended from each internal node For each node with L >= k, and N >= p, print all leaves O(m) to traverse tree (L, N)

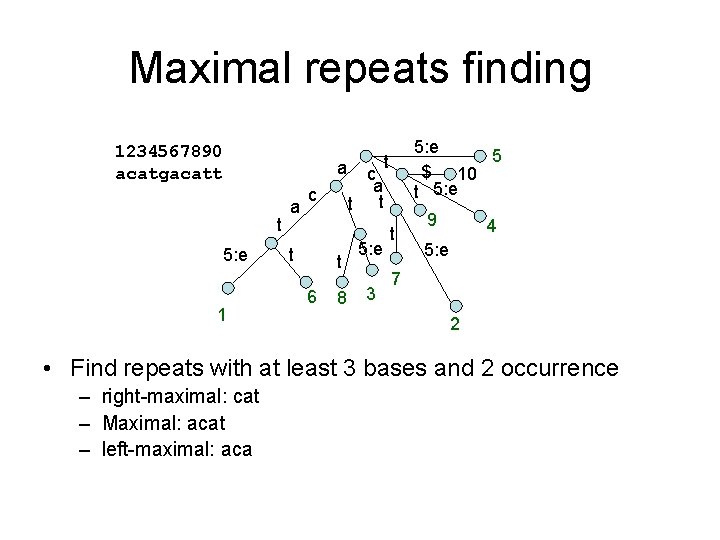
Maximal repeats finding 1. Right-maximal repeat – S[i+1. . i+k] = S[j+1. . j+k], – but S[i+k+1] != S[j+k+1] 2. Left-maximal repeat acatgacatt 1. cat 2. aca 3. acat – S[i+1. . i+k] = S[j+1. . j+k] – But S[i] != S[j] 3. Maximal repeat – S[i+1. . i+k] = S[j+1. . j+k] – But S[i] != S[j], and S[i+k+1] != S[j+k+1]

Maximal repeats finding 1234567890 acatgacatt a t 5: e 1 a c t t 6 8 5: e 5 $ 10 t 5: e t c a t t 5: e 3 t 9 4 5: e 7 2 • Find repeats with at least 3 bases and 2 occurrence – right-maximal: cat – Maximal: acat – left-maximal: aca

Maximal repeats finding 1234567890 acatgacatt a t 5: e 1 Left char = [] a c t c a t t t 6 5: e 5 $ 10 t 5: e t 8 5: e 3 9 t 4 5: e 7 2 g c c a a • How to find maximal repeat? – A right-maximal repeats with different left chars

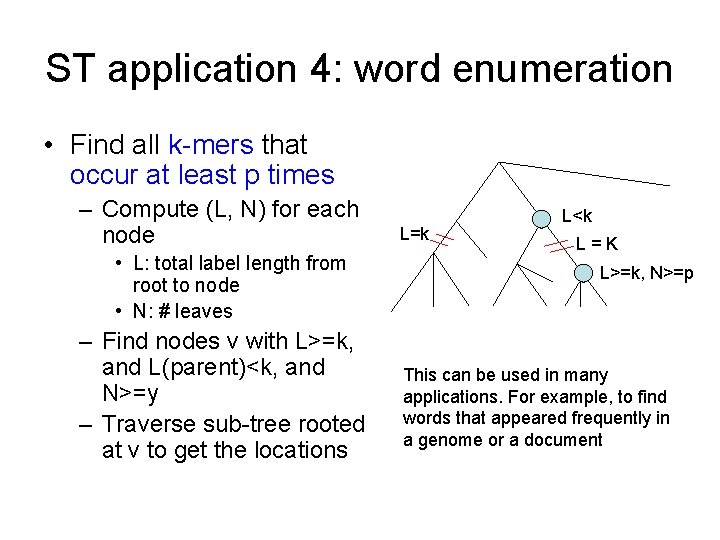
ST application 4: word enumeration • Find all k-mers that occur at least p times – Compute (L, N) for each node • L: total label length from root to node • N: # leaves – Find nodes v with L>=k, and L(parent)<k, and N>=y – Traverse sub-tree rooted at v to get the locations L=k L<k L=K L>=k, N>=p This can be used in many applications. For example, to find words that appeared frequently in a genome or a document

Joint Suffix Tree • • • Build a ST for many than two strings Two strings S 1 and S 2 S* = S 1 & S 2 Build a suffix tree for S* in time O(|S 1| + |S 2|) The separator will only appear in the edge ending in a leaf

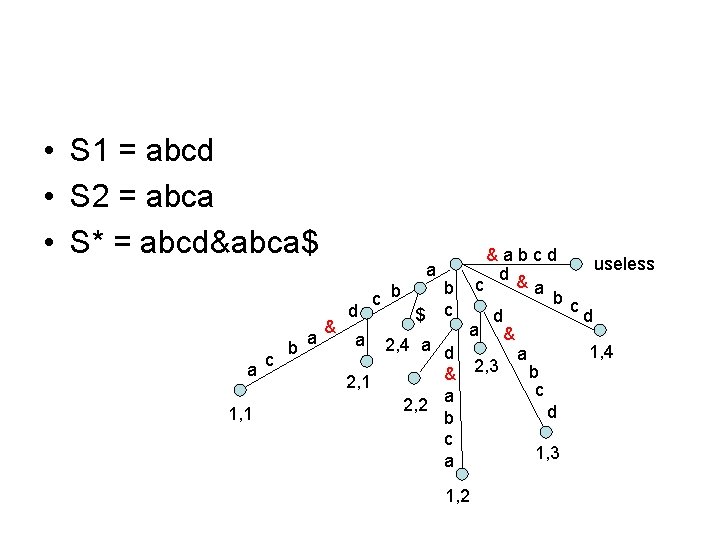
• S 1 = abcd • S 2 = abca • S* = abcd&abca$ a 1, 1 c b a a & d a c b $ b c 2, 4 a d & 2, 1 a 2, 2 b c a &abcd useless d & c a b c d d a & 1, 4 a 2, 3 b c d 1, 2 1, 3

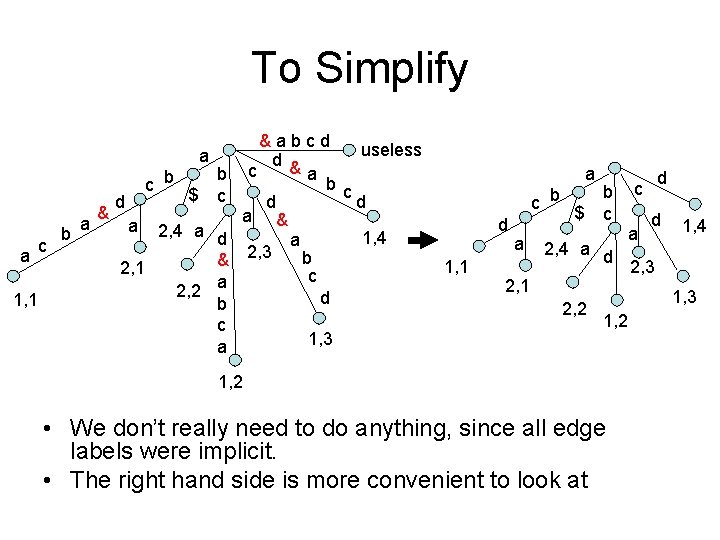
To Simplify a a 1, 1 c b a & c b d a $ b c 2, 4 a d & 2, 1 a 2, 2 b c a &abcd useless d & c a b c d d a & 1, 4 a 2, 3 b c d 1, 3 a c b d 1, 1 a $ b c 2, 4 a d 2, 1 2, 2 d c a d 1, 4 2, 3 1, 2 • We don’t really need to do anything, since all edge labels were implicit. • The right hand side is more convenient to look at

Application of JST • Longest common substring – For each internal node v, keep a bit vector B – B[1] = 1 if a child of v is a suffix of S 1 – Find all internal nodes with B[1] = B[2] = 1 – Report one with the longest label – Can be extended to k sequences. Just use a longer bit vector. Not subsequence a c b d 1, 1 a $ b c 2, 4 a d 2, 1 2, 2 d c a d 1, 4 2, 3 1, 2

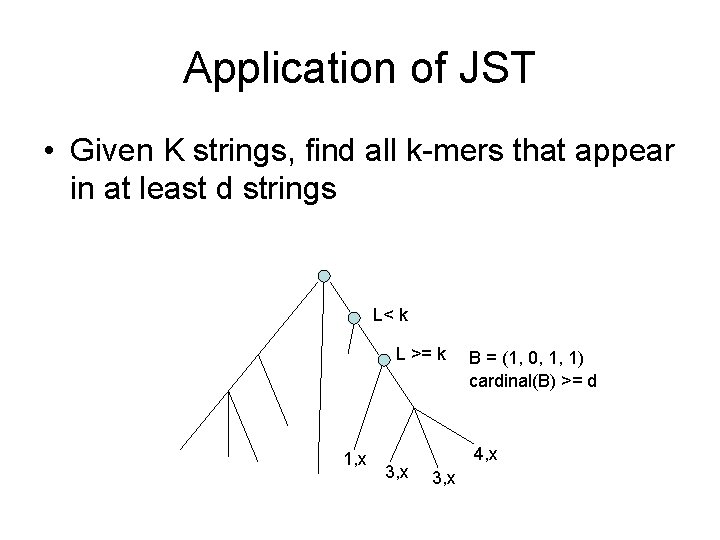
Application of JST • Given K strings, find all k-mers that appear in at least d strings L< k L >= k 1, x 3, x B = (1, 0, 1, 1) cardinal(B) >= d 4, x 3, x

Many other applications • Reproduce the behavior of Aho-Corasick • Recognizing computer virus – A database of known computer viruses – Does a file contain virus? • DNA finger printing – A database of people’s DNA sequence – Given a short DNA, which person is it from? • … • Catch – Large constant factor for space requirement – Large constant factor for construction – Suffix array: trade off time for space

Summary • One T, one P – Boyer-Moore is the choice – KMP works but not the best Alphabet independent • One T, many P – Aho-Corasick – Suffix Tree Alphabet dependent • One fixed T, many varying P – Suffix tree • Two or more T’s – Suffix tree, joint suffix tree, suffix array

Pattern pre-processing algs – Karp – Rabin algorithm • Small alphabet and small pattern – Boyer – Moore algorithm • The choice of most cases • Typically sub-linear time – Knuth-Morris-Pratt algorithm (KMP) – Aho-Corasick algorithm • The algorithm for the unix utility fgrep – Suffix tree • One of the most useful preprocessing techniques • Many applications

Karp – Rabin Algorithm • Let’s say we are dealing with binary numbers Text: 0101000101100101001 Pattern: 101100 • Convert pattern to integer 101100 = 2^5 + 2^3 + 2^2 = 44

Karp – Rabin algorithm Text: 0101000101100101001 Pattern: 101100 = 44 decimal 101100101001 = 2^5 + 0 + 2^3 + 2^2 + 2^1 = 46 101100101001 = 46 * 2 – 64 + 1 = 29 101100101001 = 29 * 2 - 0 + 1 = 59 101100101001 = 59 * 2 - 64 + 0 = 54 101100101001 = 54 * 2 - 64 + 0 = 44 Θ(m+n)

Karp – Rabin algorithm What if the pattern is too long to fit into a single integer? Pattern: 101100. What if each word in our computer has only 4 bits? Basic idea: hashing. 44 % 13 = 5 101100101001 = 46 (% 13 = 7) 101100101001 = 46 * 2 – 64 + 1 = 29 (% 13 = 3) 101100101001 = 29 * 2 - 0 + 1 = 59 (% 13 = 7) 101100101001 = 59 * 2 - 64 + 0 = 54 (% 13 = 2) 101100101001 = 54 * 2 - 64 + 0 = 44 (% 13 = 5) Θ(m+n) expected running time

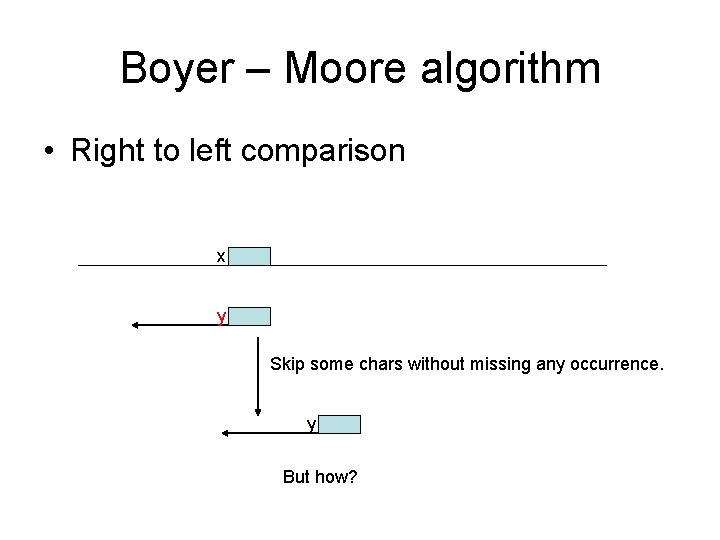
Boyer – Moore algorithm • Three ideas: – Right-to-left comparison – Bad character rule – Good suffix rule

Boyer – Moore algorithm • Right to left comparison x y Skip some chars without missing any occurrence. y But how?

Bad character rule 0 1 12345678901234567 T: xpbctbxabpqqaabpq P: tpabxab *^^^^ What would you do now?

Bad character rule 0 1 12345678901234567 T: xpbctbxabpqqaabpq P: tpabxab *^^^^ P: tpabxab

Bad character rule 0 1 123456789012345678 T: xpbctbxabpqqaabpqz P: tpabxab *^^^^ P: tpabxab * P: tpabxab

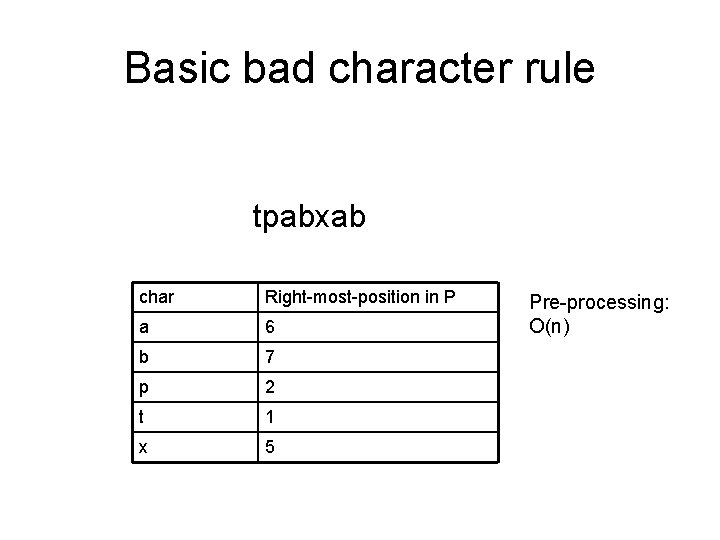
Basic bad character rule tpabxab char Right-most-position in P a 6 b 7 p 2 t 1 x 5 Pre-processing: O(n)

Basic bad character rule k T: xpbctbxabpqqaabpqz P: tpabxab When rightmost T(k) in *^^^^ P is left to i, shift pattern P to align T(k) with the rightmost T(k) in P i=3 Shift 3 – 1 = 2 P: tpabxab char Right-most-position in P a 6 b 7 p 2 t 1 x 5

Basic bad character rule k T: xpbctbxabpqqaabpqz P: tpabxab * When T(k) is not in i=7 P, shift left end of P to align with T(k+1) Shift 7 – 0 = 7 P: tpabxab char Right-most-position in P a 6 b 7 p 2 t 1 x 5

Basic bad character rule k T: xpbctbxabpqqaabpqz P: tpabxab When rightmost T(k) *^^ in P is right to i, shift pattern P one pos i=5 P: tpabxab char Right-most-position in P a 6 b 7 p 2 t 1 x 5 5 – 6 < 0. so shift 1

Extended bad character rule k T: xpbctbxabpqqaabpqz P: tpabxab *^^ Find T(k) in P that is immediately left to i, shift P to align T(k) with that position i=5 5 – 3 = 2. so shift 2 P: tpabxab char Position in P a 6, 3 b 7, 4 p 2 t 1 x 5 Preprocessing still O(n)

Extended bad character rule • Best possible: m / n comparisons • Works better for large alphabet size • In some cases the extended bad character rule is sufficiently good • Worst-case: O(mn) • What else can we do?

0 1 123456789012345678 T: prstabstubabvqxrst P: qcabdabdab *^^ According to extended bad character rule P: qcabdabdab

(weak) good suffix rule 0 1 123456789012345678 T: prstabstubabvqxrst P: qcabdabdab *^^ P: qcabdabdab

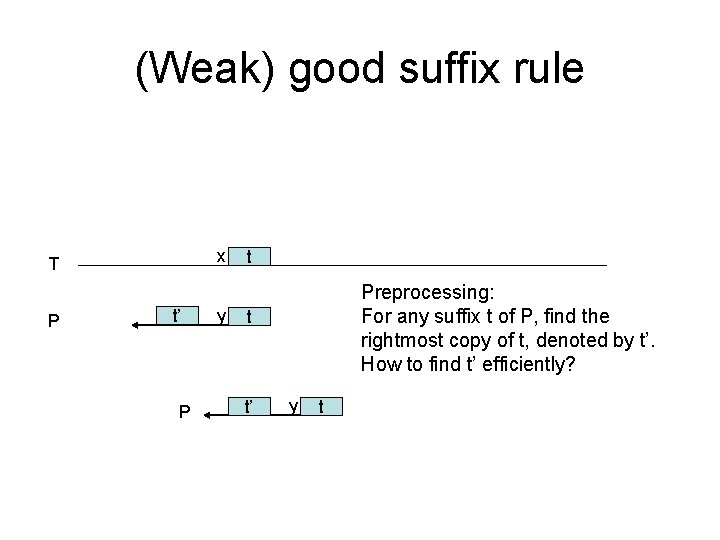
(Weak) good suffix rule x T P t’ P y t Preprocessing: For any suffix t of P, find the rightmost copy of t, denoted by t’. How to find t’ efficiently? t t’ y t

(Strong) good suffix rule 0 1 123456789012345678 T: prstabstubabvqxrst P: qcabdabdab *^^

(Strong) good suffix rule 0 1 123456789012345678 T: prstabstubabvqxrst P: qcabdabdab *^^ P: qcabdabdab

(Strong) good suffix rule 0 1 123456789012345678 T: prstabstubabvqxrst P: qcabdabdab *^^ P: qcabdabdab

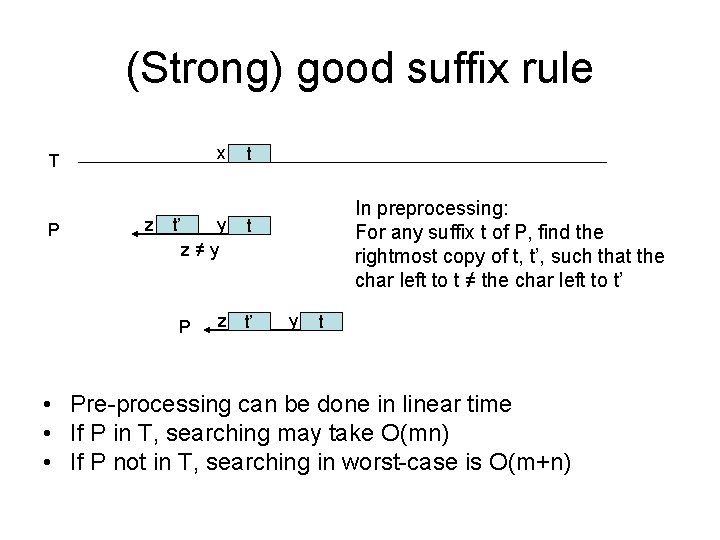
(Strong) good suffix rule x T P z t’ y z≠y P t In preprocessing: For any suffix t of P, find the rightmost copy of t, t’, such that the char left to t ≠ the char left to t’ t z t’ y t • Pre-processing can be done in linear time • If P in T, searching may take O(mn) • If P not in T, searching in worst-case is O(m+n)

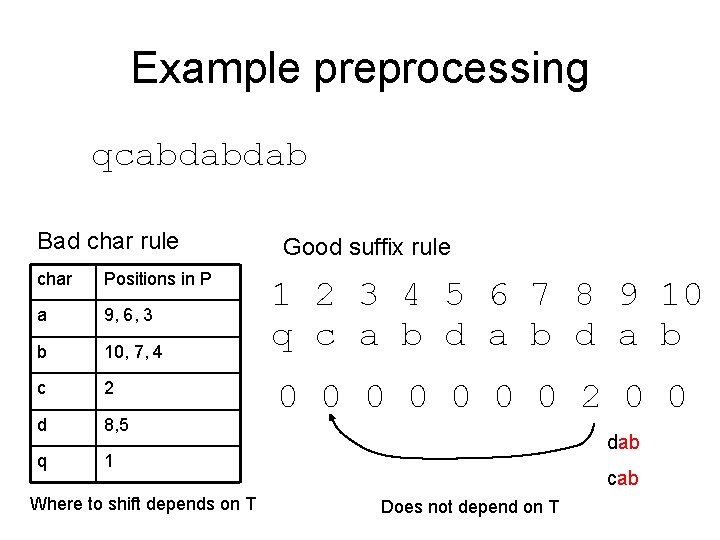
Example preprocessing qcabdabdab Bad char rule char Positions in P a 9, 6, 3 b 10, 7, 4 c 2 d 8, 5 q 1 Where to shift depends on T Good suffix rule 1 2 3 4 5 6 7 8 9 10 q c a b d a b 0 0 0 0 2 0 0 dab cab Does not depend on T