CS 3343 Analysis of Algorithms Lecture 24 Graph

CS 3343: Analysis of Algorithms Lecture 24: Graph searching, Topological sort

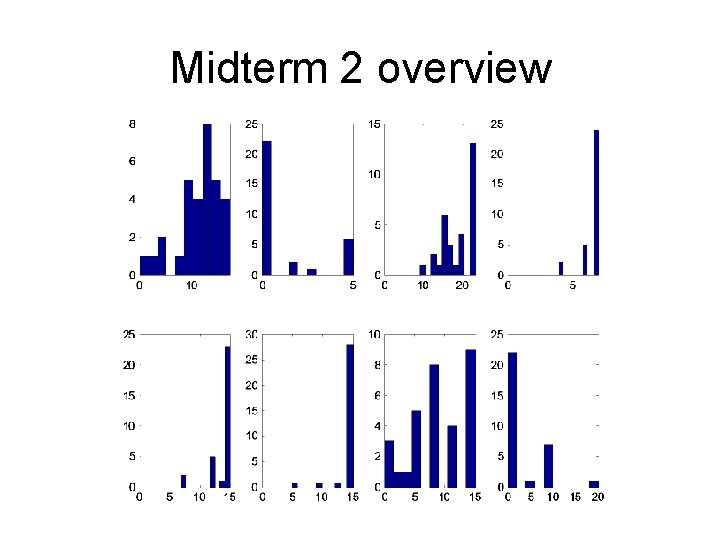
Midterm 2 overview

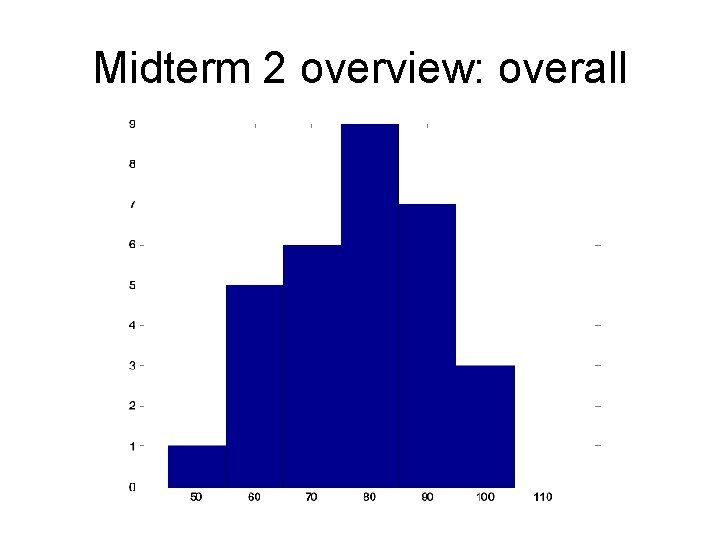
Midterm 2 overview: overall

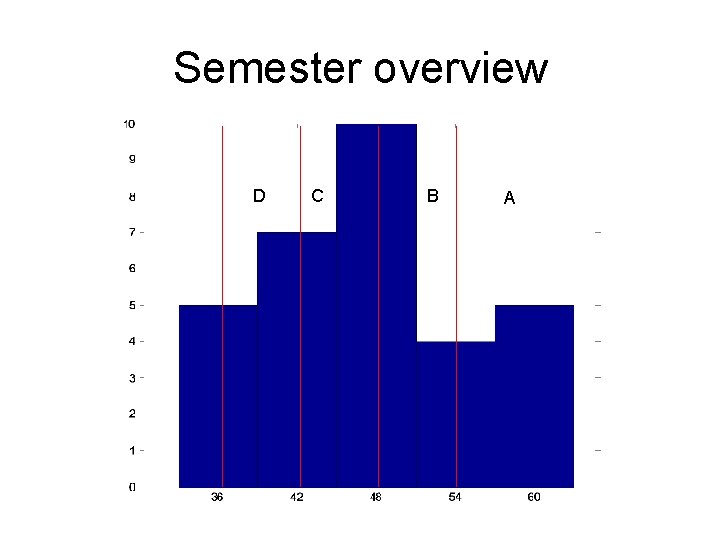
Semester overview D C B A

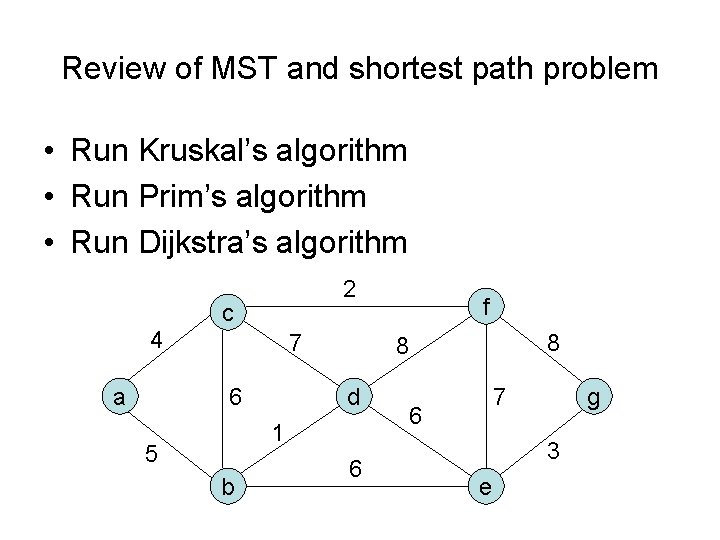
Review of MST and shortest path problem • Run Kruskal’s algorithm • Run Prim’s algorithm • Run Dijkstra’s algorithm 2 c 4 a 7 1 5 b 8 8 d 6 f 6 g 7 6 3 e

Graph Searching • Given: a graph G = (V, E), directed or undirected • Goal: methodically explore every vertex (and every edge) • Ultimately: build a tree on the graph – Pick a vertex as the root – Find (“discover”) its children, then their children, etc. – Note: might also build a forest if graph is not connected – Here we only consider that the graph is connected

Breadth-First Search • “Explore” a graph, turning it into a tree – Pick a source vertex to be the root – Expand frontier of explored vertices across the breadth of the frontier

Breadth-First Search • Associate vertex “colors” to guide the algorithm – White vertices have not been discovered • All vertices start out white – Grey vertices are discovered but not fully explored • They may be adjacent to white vertices – Black vertices are discovered and fully explored • They are adjacent only to black and gray vertices • Explore vertices by scanning adjacency list of grey vertices

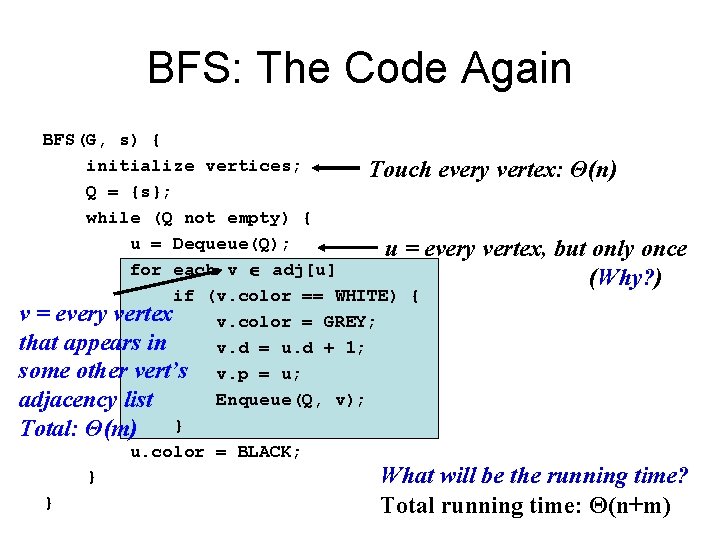
Breadth-First Search BFS(G, s) { initialize vertices; // mark all vertices as white Q = {s}; // Q is a queue; initialize to s while (Q not empty) { u = Dequeue(Q); for each v adj[u] if (v. color == WHITE) { v. color = GREY; What does v. d represent? v. d = u. d + 1; What does v. p represent? v. p = u; Enqueue(Q, v); } u. color = BLACK; } }

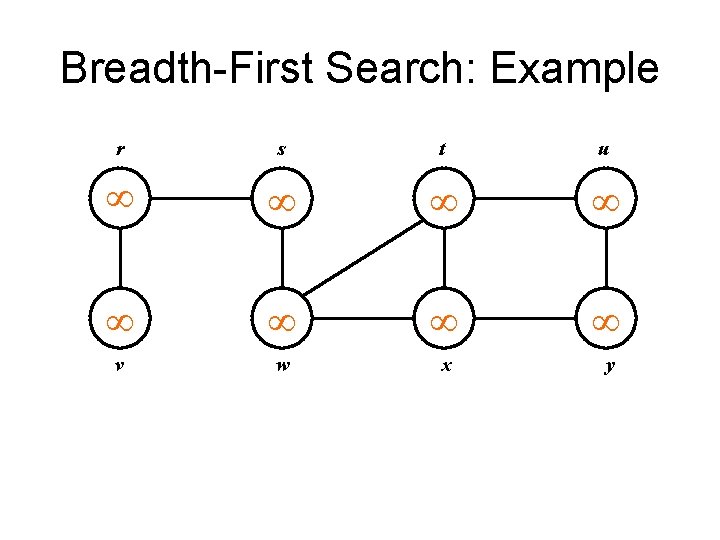
Breadth-First Search: Example r s t u v w x y

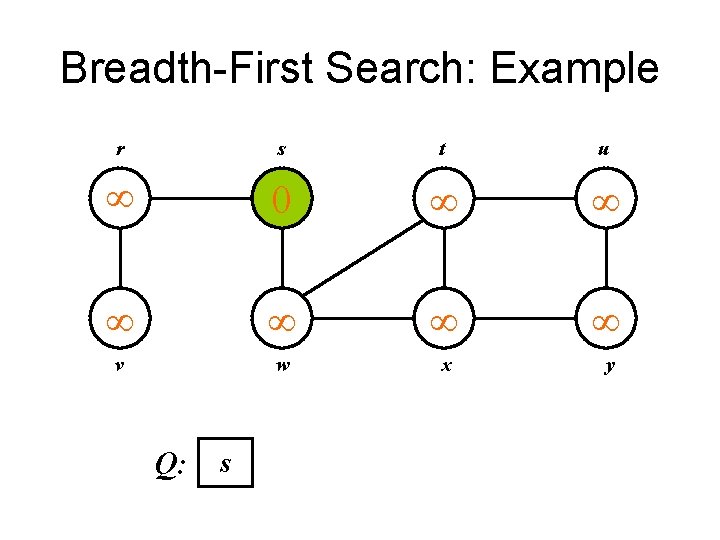
Breadth-First Search: Example r s t u 0 v w x y Q: s

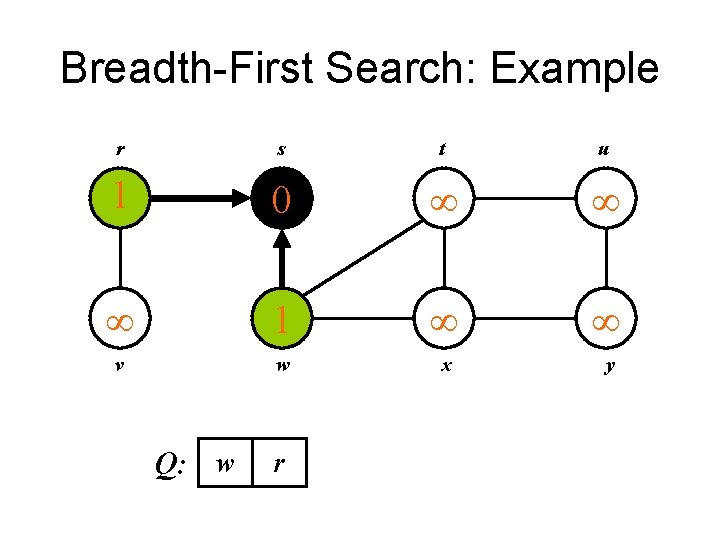
Breadth-First Search: Example r s t u 1 0 1 v w x y Q: w r

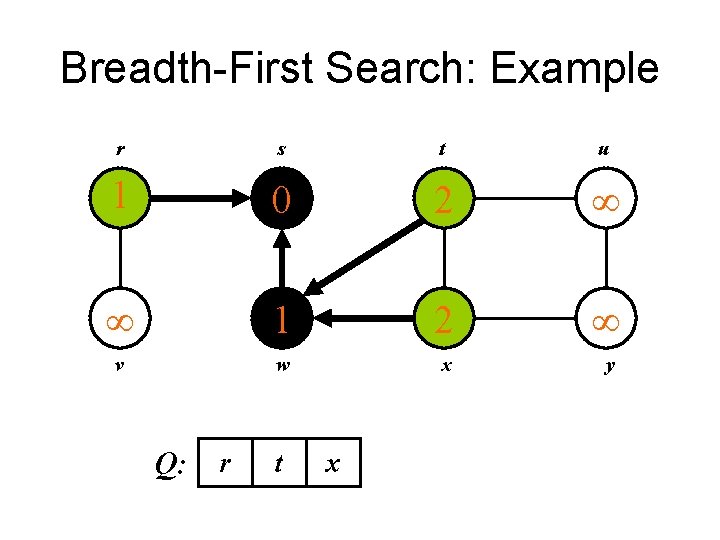
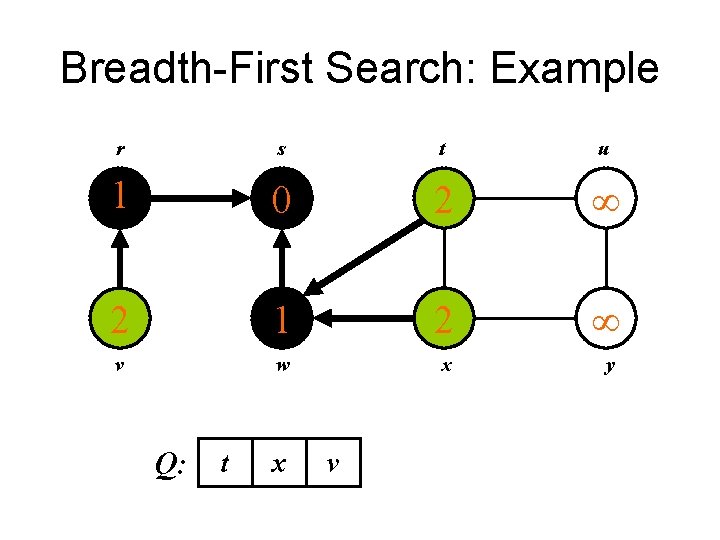
Breadth-First Search: Example r s t u 1 0 2 1 2 v w x y Q: r t x

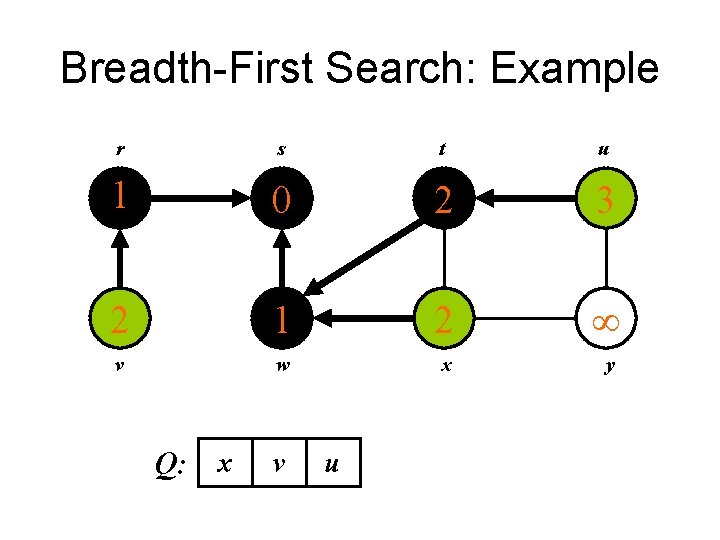
Breadth-First Search: Example r s t u 1 0 2 2 1 2 v w x y Q: t x v

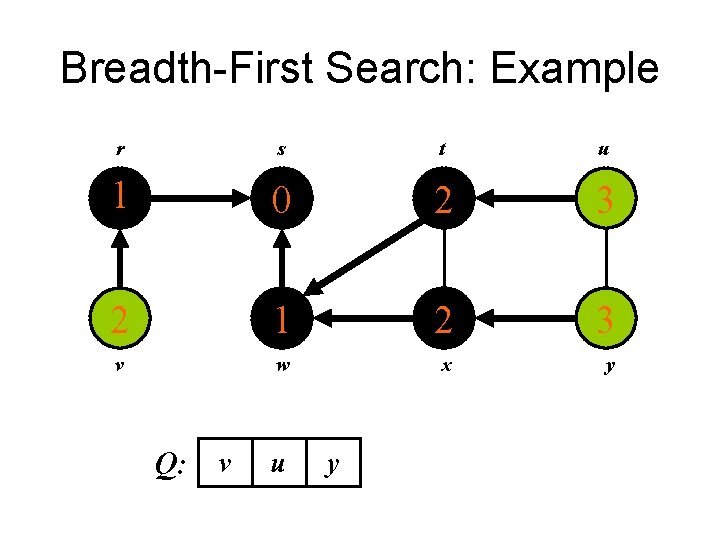
Breadth-First Search: Example r s t u 1 0 2 3 2 1 2 v w x y Q: x v u

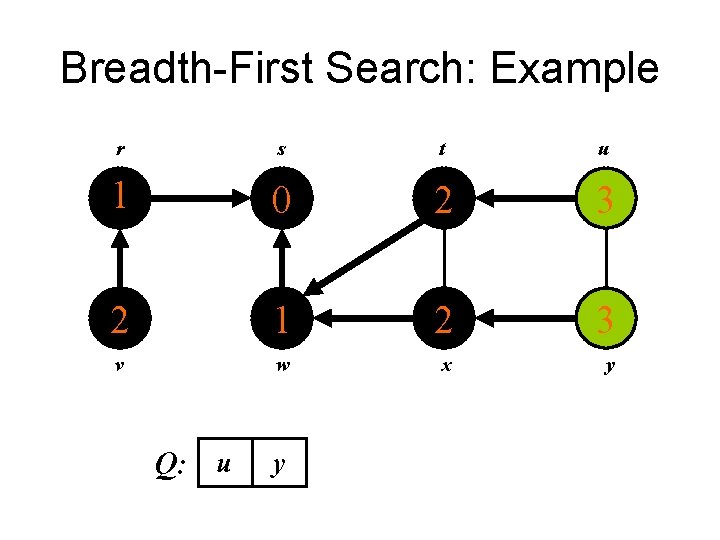
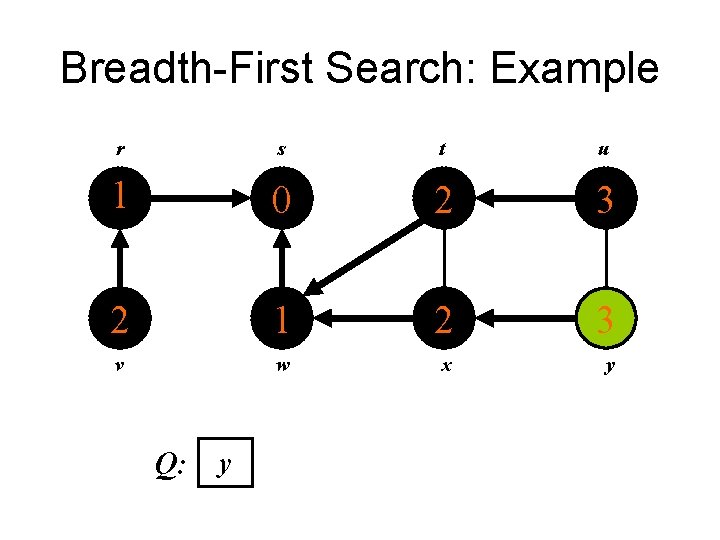
Breadth-First Search: Example r s t u 1 0 2 3 2 1 2 3 v w x y Q: v u y

Breadth-First Search: Example r s t u 1 0 2 3 2 1 2 3 v w x y Q: u y

Breadth-First Search: Example r s t u 1 0 2 3 2 1 2 3 v w x y Q: y

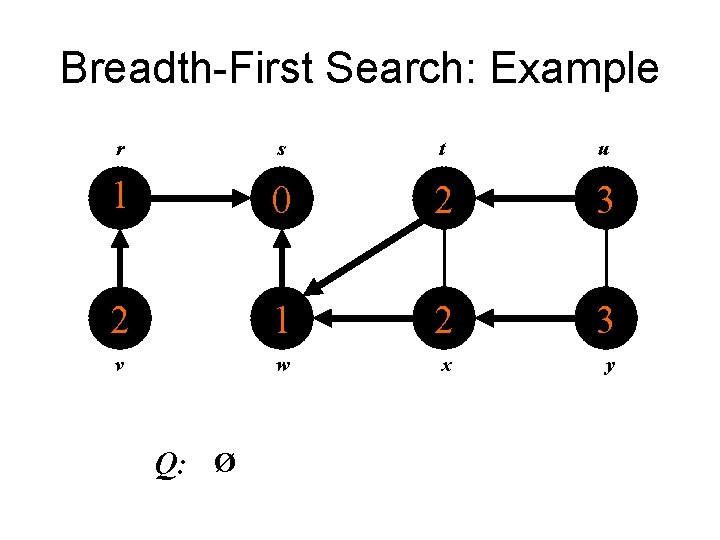
Breadth-First Search: Example r s t u 1 0 2 3 2 1 2 3 v w x y Q: Ø

BFS: The Code Again BFS(G, s) { initialize vertices; Touch every vertex: Θ(n) Q = {s}; while (Q not empty) { u = Dequeue(Q); u = every vertex, but only once for each v adj[u] (Why? ) if (v. color == WHITE) { v = every vertex v. color = GREY; that appears in v. d = u. d + 1; some other vert’s v. p = u; Enqueue(Q, v); adjacency list Total: Θ(m) } u. color = BLACK; } What will be the running time? } Total running time: Θ(n+m)

Depth-First Search • Depth-first search is another strategy for exploring a graph – Explore “deeper” in the graph whenever possible – Edges are explored out of the most recently discovered vertex v that still has unexplored edges – When all of v’s edges have been explored, backtrack to the vertex from which v was discovered

Depth-First Search • Vertices initially colored white • Then colored gray when discovered • Then black when finished

Depth-First Search: The Code DFS(G) { for each vertex u G->V { u->color = WHITE; } time = 0; for each vertex u G->V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; }

Depth-First Search: The Code DFS(G) { for each vertex u G->V { u->color = WHITE; } time = 0; for each vertex u G->V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; } What does u->d represent?

Depth-First Search: The Code DFS(G) { for each vertex u G->V { u->color = WHITE; } time = 0; for each vertex u G->V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; } What does u->f represent?

Depth-First Search: The Code DFS(G) { for each vertex u G->V { u->color = WHITE; } time = 0; for each vertex u G->V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; } Will all vertices eventually be colored black? (How about in BFS? )

Depth-First Search: The Code DFS(G) { for each vertex u G->V { u->color = WHITE; } time = 0; for each vertex u G->V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; } What will be the running time?

Depth-First Search: The Code DFS(G) { for each vertex u G->V { u->color = WHITE; } time = 0; for each vertex u G->V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; } How many times will DFS_Visit() be called?

Depth-First Search: The Code DFS(G) { for each vertex u G->V { u->color = WHITE; } time = 0; for each vertex u G->V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; } How much time is needed within each DFS_Visit()?

Depth-First Search: The Code DFS(G) { for each vertex u G->V { u->color = WHITE; } time = 0; for each vertex u G->V { if (u->color == WHITE) DFS_Visit(u); } } DFS_Visit(u) { u->color = GREY; time = time+1; u->d = time; for each v u->Adj[] { if (v->color == WHITE) DFS_Visit(v); } u->color = BLACK; time = time+1; u->f = time; } So, running time of DFS = O(V+E)

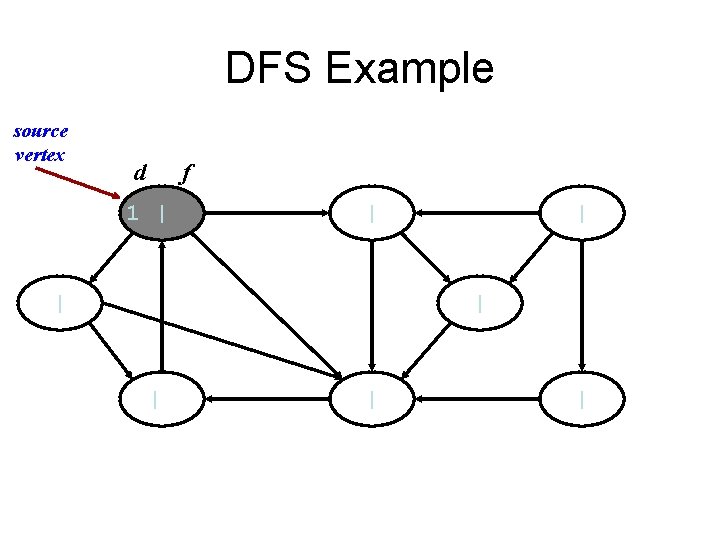
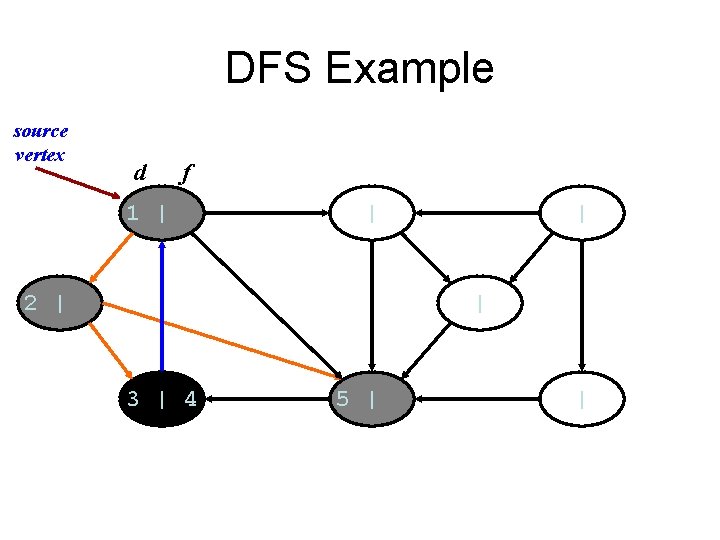
DFS Example source vertex

DFS Example source vertex d f 1 | | | |

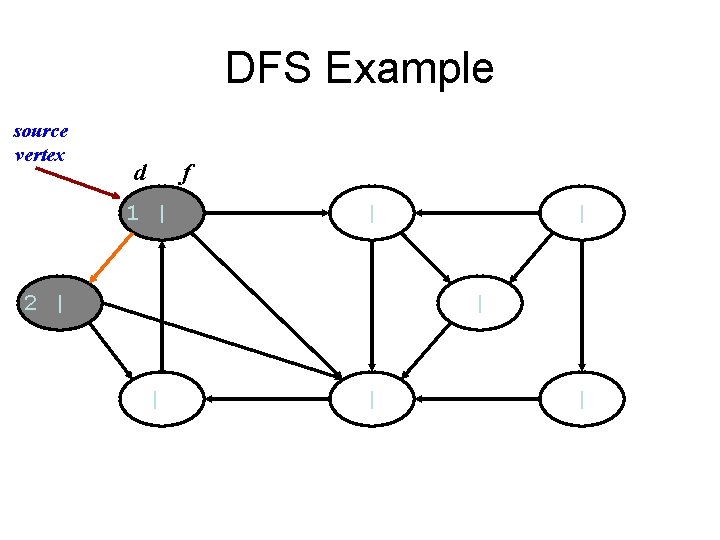
DFS Example source vertex d f 1 | | 2 | | |

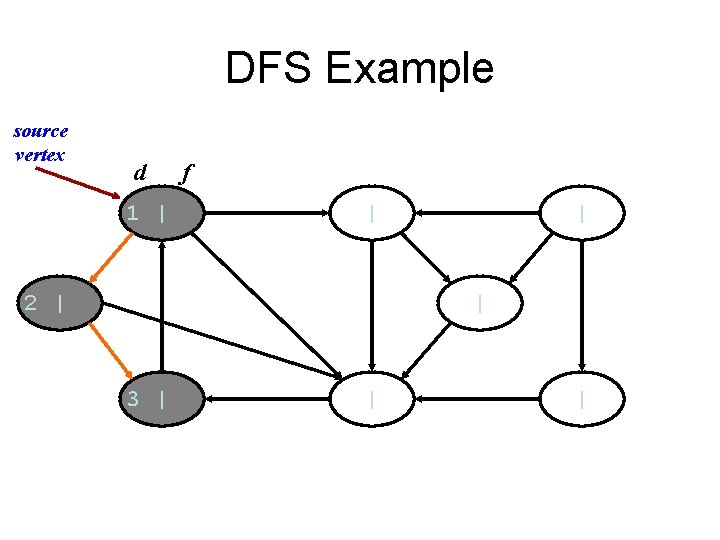
DFS Example source vertex d 1 | f | 2 | | | 3 | | |

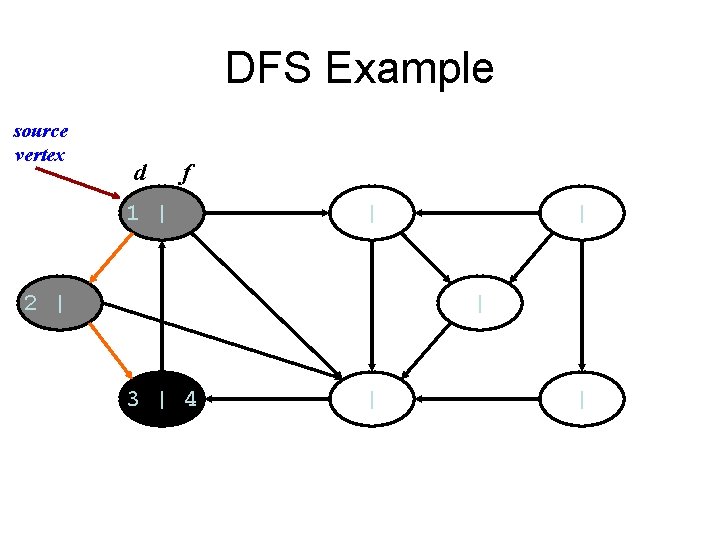
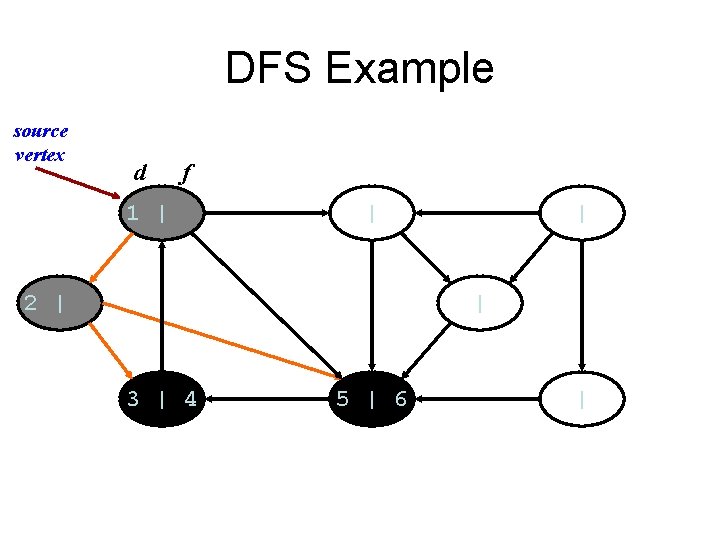
DFS Example source vertex d f 1 | | 2 | | | 3 | 4 | |

DFS Example source vertex d f 1 | | 2 | | | 3 | 4 5 | |

DFS Example source vertex d f 1 | | 2 | | | 3 | 4 5 | 6 |

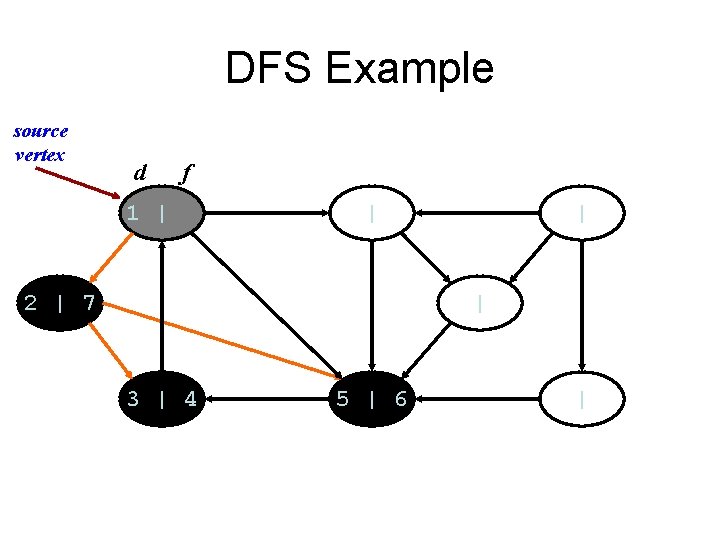
DFS Example source vertex d f 1 | | 2 | 7 | | 3 | 4 5 | 6 |

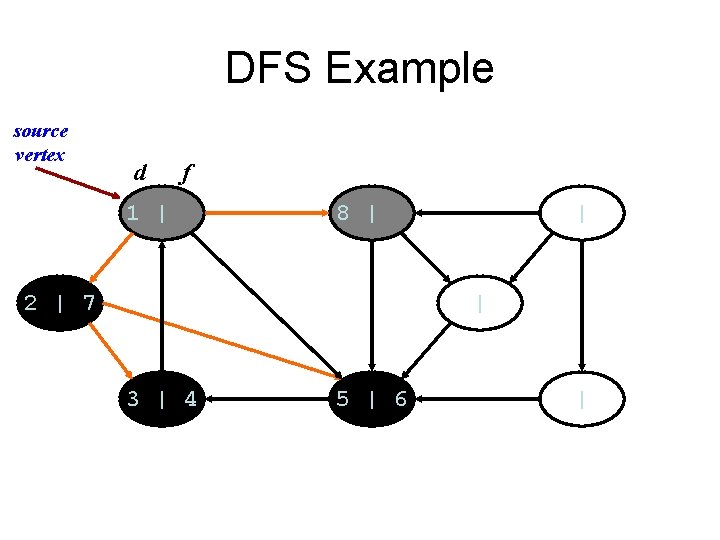
DFS Example source vertex d f 1 | 8 | 2 | 7 | | 3 | 4 5 | 6 |

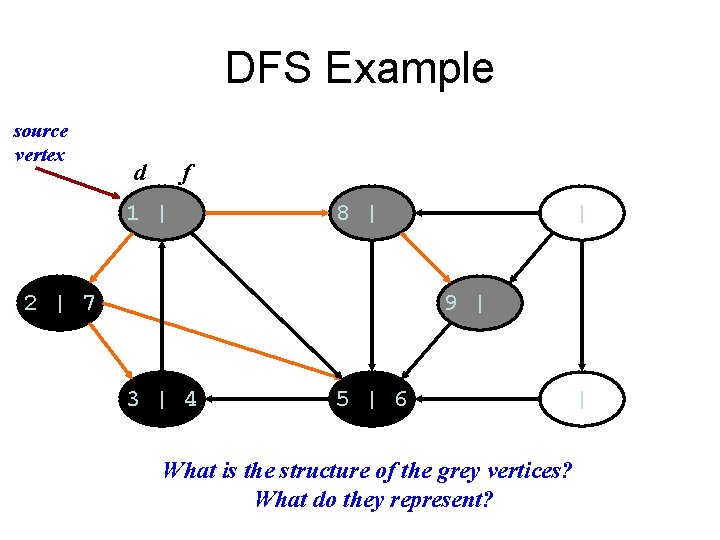
DFS Example source vertex d f 1 | 8 | 2 | 7 | 9 | 3 | 4 5 | 6 What is the structure of the grey vertices? What do they represent? |

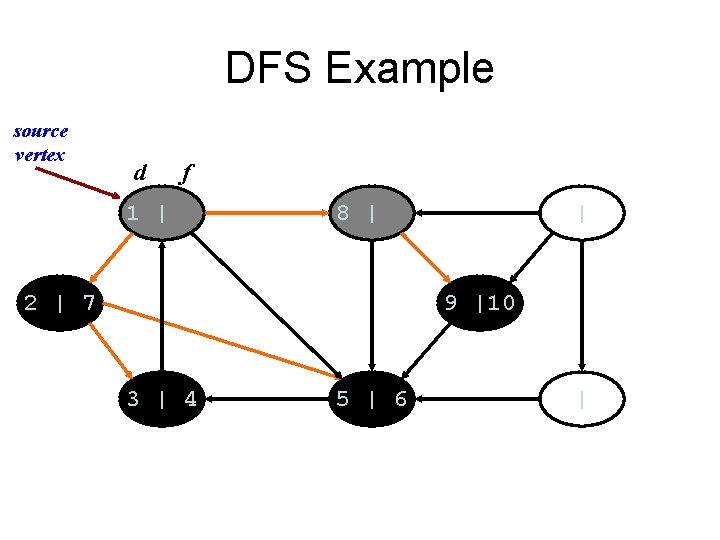
DFS Example source vertex d f 1 | 8 | 2 | 7 | 9 |10 3 | 4 5 | 6 |

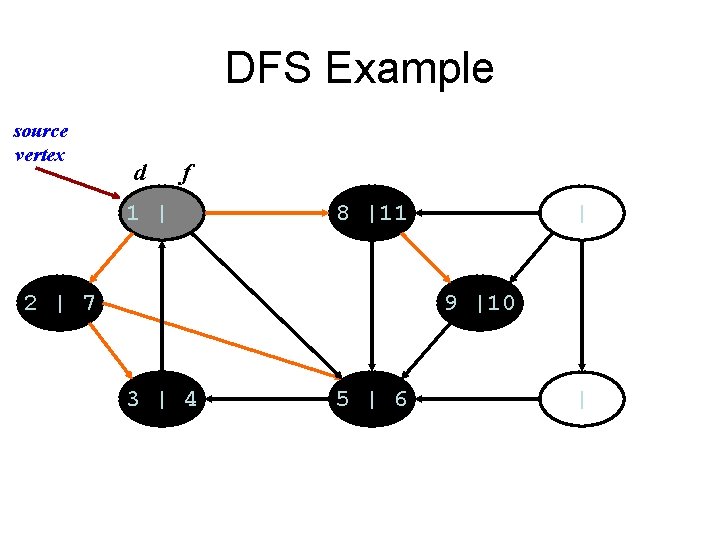
DFS Example source vertex d f 1 | 8 |11 2 | 7 | 9 |10 3 | 4 5 | 6 |

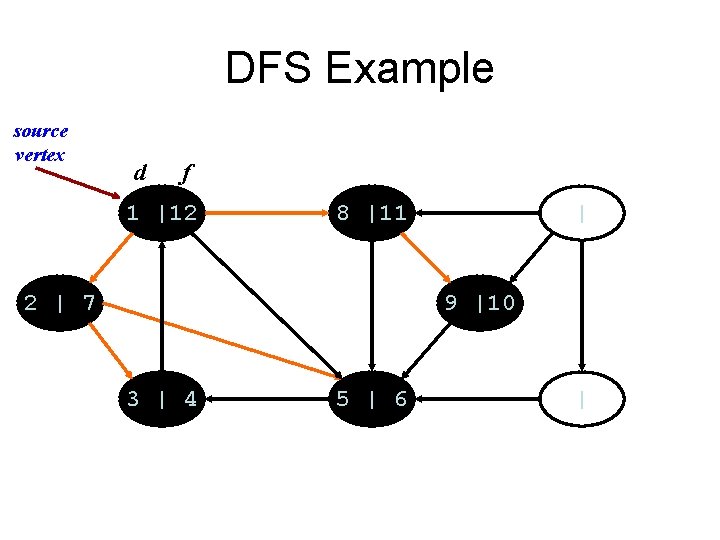
DFS Example source vertex d f 1 |12 8 |11 2 | 7 | 9 |10 3 | 4 5 | 6 |

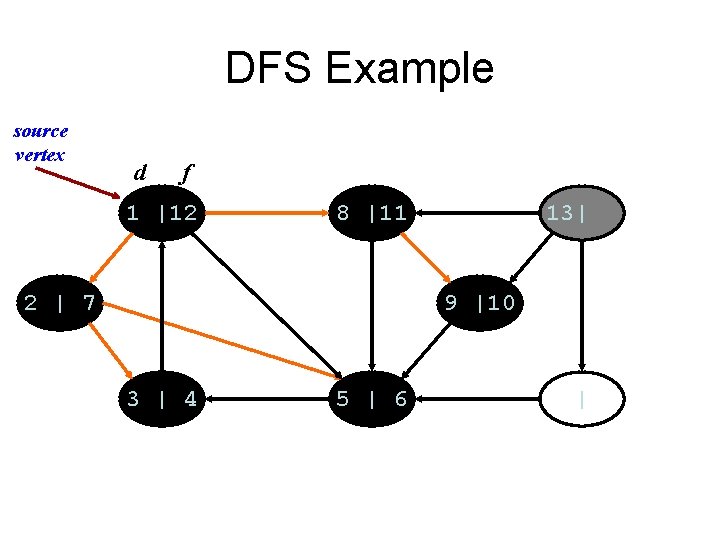
DFS Example source vertex d f 1 |12 8 |11 2 | 7 13| 9 |10 3 | 4 5 | 6 |

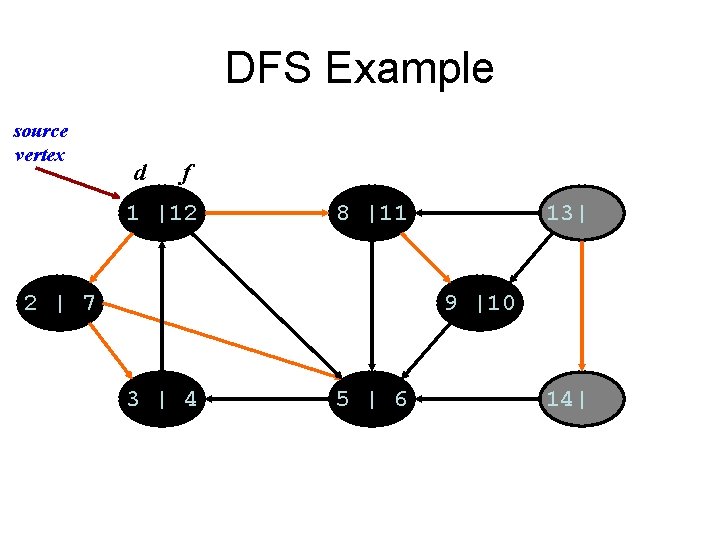
DFS Example source vertex d f 1 |12 8 |11 2 | 7 13| 9 |10 3 | 4 5 | 6 14|

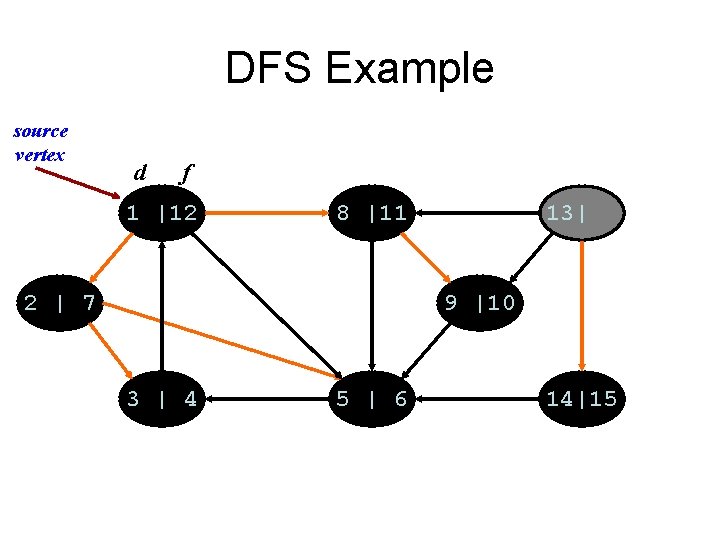
DFS Example source vertex d f 1 |12 8 |11 2 | 7 13| 9 |10 3 | 4 5 | 6 14|15

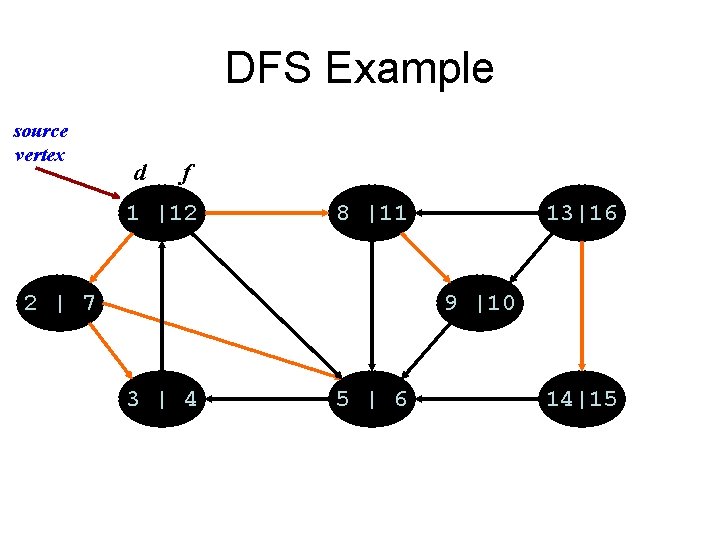
DFS Example source vertex d f 1 |12 8 |11 2 | 7 13|16 9 |10 3 | 4 5 | 6 14|15

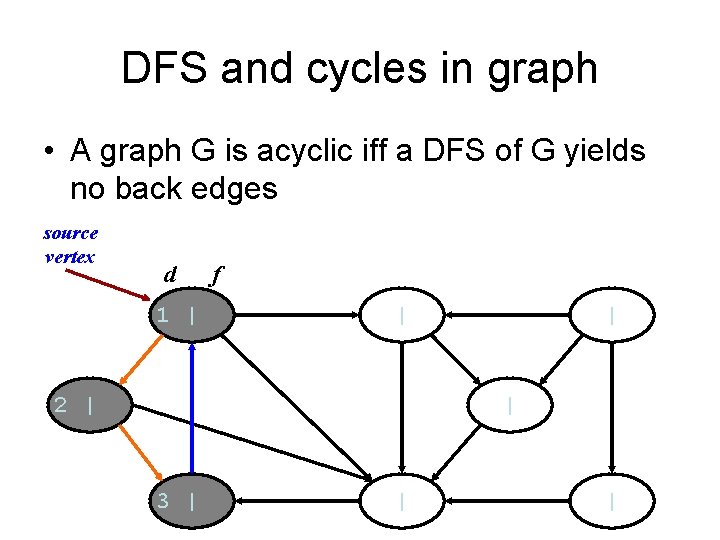
DFS and cycles in graph • A graph G is acyclic iff a DFS of G yields no back edges source vertex d 1 | f | 2 | | | 3 | | |

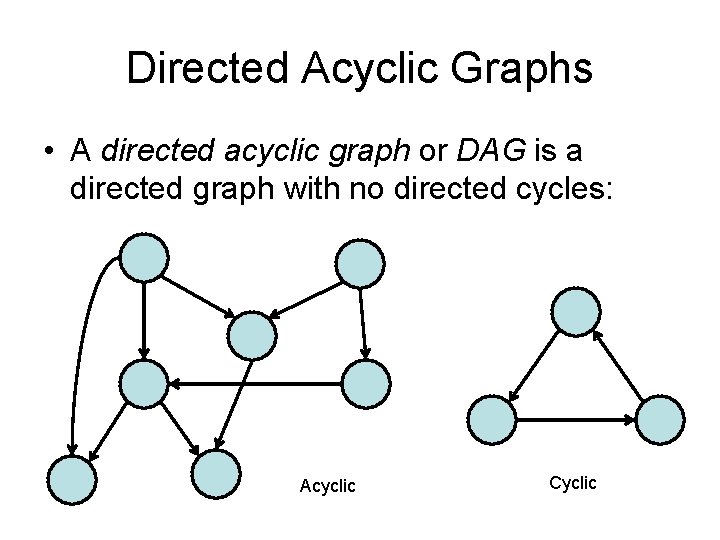
Directed Acyclic Graphs • A directed acyclic graph or DAG is a directed graph with no directed cycles: Acyclic Cyclic

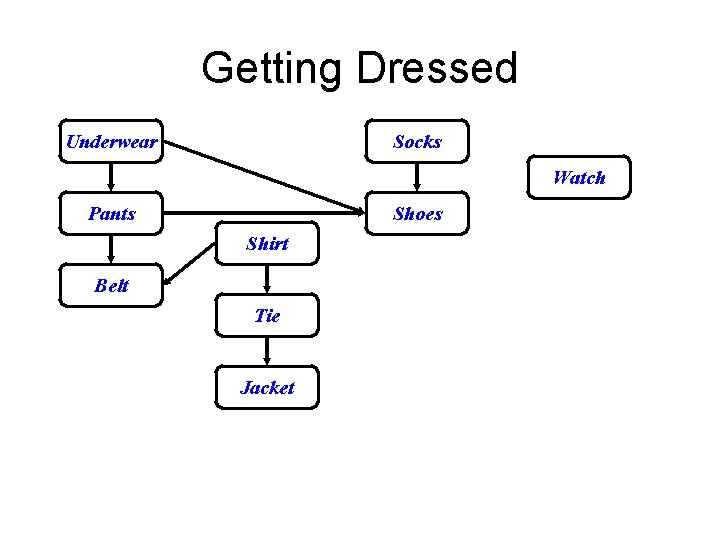
Topological Sort • Topological sort of a DAG: – Linear ordering of all vertices in graph G such that vertex u comes before vertex v if edge (u, v) G • Real-world example: getting dressed

Getting Dressed Underwear Socks Watch Pants Shoes Shirt Belt Tie Jacket

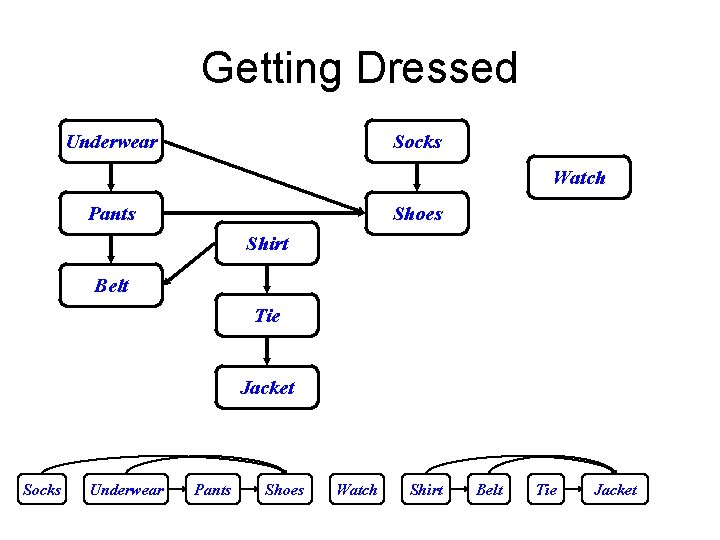
Getting Dressed Underwear Socks Watch Pants Shoes Shirt Belt Tie Jacket Socks Underwear Pants Shoes Watch Shirt Belt Tie Jacket

Topological Sort Algorithm Topological-Sort() { // condition: the graph is a DAG Run DFS When a vertex is finished, output it Vertices are output in reverse topological order } • Time: O(V+E) • Correctness: Want to prove that (u, v) G u f > v f

Correctness of Topological Sort • Claim: (u, v) G u f > v f – When (u, v) is explored, u is grey • v = grey (u, v) is back edge. Contradiction (Why? ) • v = white v becomes descendent of u v f < u f (since must finish v before backtracking and finishing u) • v = black v already finished v f < u f

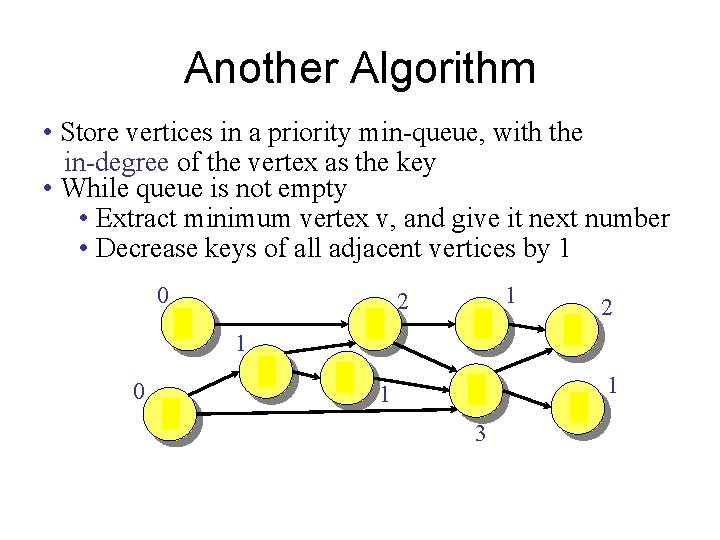
Another Algorithm • Store vertices in a priority min-queue, with the in-degree of the vertex as the key • While queue is not empty • Extract minimum vertex v, and give it next number • Decrease keys of all adjacent vertices by 1 0 0 2 1 1 4 3 5 1 2 7 6 3 1 8 9 2 1

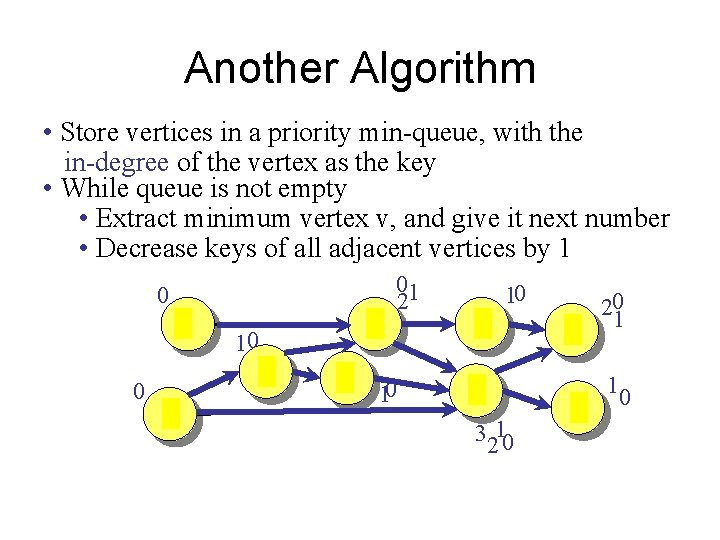
Another Algorithm • Store vertices in a priority min-queue, with the in-degree of the vertex as the key • While queue is not empty • Extract minimum vertex v, and give it next number • Decrease keys of all adjacent vertices by 1 0 0 1 10 3 2 4 5 01 2 10 7 10 6 3210 8 9 201 10

Topological Sort Runtime: • O(|V|) to build heap + O(|E|) DECREASE-KEY ops O(|V| + |E| log |V|) with a binary heap O(|V|2) with an array Compare to DFS: O(|V|+|E|)