CS 3343 Analysis of Algorithms Lecture 14 Order

CS 3343: Analysis of Algorithms Lecture 14: Order Statistics

Order statistics • The ith order statistic in a set of n elements is the ith smallest element • The minimum is thus the 1 st order statistic • The maximum is the nth order statistic • The median is the n/2 order statistic • If n is even, there are 2 medians • How can we calculate order statistics? • What is the running time?

Order statistics – selection problem • Select the ith smallest of n elements • Naive algorithm: Sort. – Worst-case running time Q(n log n) using merge sort or heapsort (not quicksort). • We will show: – A practical randomized algorithm with Q(n) expected running time – A cool algorithm of theoretical interest only with Q(n) worst-case running time

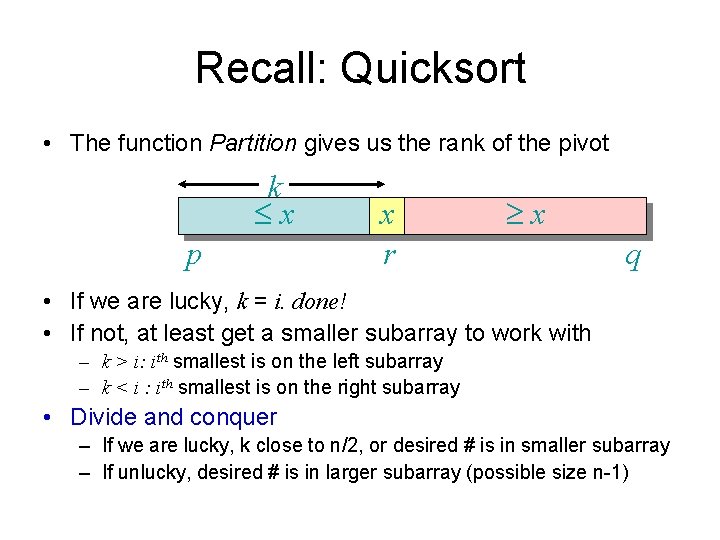
Recall: Quicksort • The function Partition gives us the rank of the pivot k x p x r x q • If we are lucky, k = i. done! • If not, at least get a smaller subarray to work with – k > i: ith smallest is on the left subarray – k < i : ith smallest is on the right subarray • Divide and conquer – If we are lucky, k close to n/2, or desired # is in smaller subarray – If unlucky, desired # is in larger subarray (possible size n-1)

Randomized divide-and-conquer algorithm RAND-SELECT(A, p, q, i) ⊳ i th smallest of A[ p. . q] if p = q & i > 1 then error! r RAND-PARTITION(A, p, q) k r–p+1 ⊳ k = rank(A[r]) if i = k then return A[ r] if i < k then return RAND-SELECT( A, p, r – 1, i ) else return RAND-SELECT( A, r + 1, q, i – k ) k A[r] p A[r] r q

Randomized Partition • Randomly choose an element as pivot – Every time need to do a partition, throw a die to decide which element to use as the pivot – Each element has 1/n probability to be selected Rand-Partition(A, p, q){ d = random(); // draw a random number between 0 and 1 index = p + floor((q-p+1) * d); // p<=index<=q swap(A[p], A[index]); Partition(A, p, q); // now use A[p] as pivot }

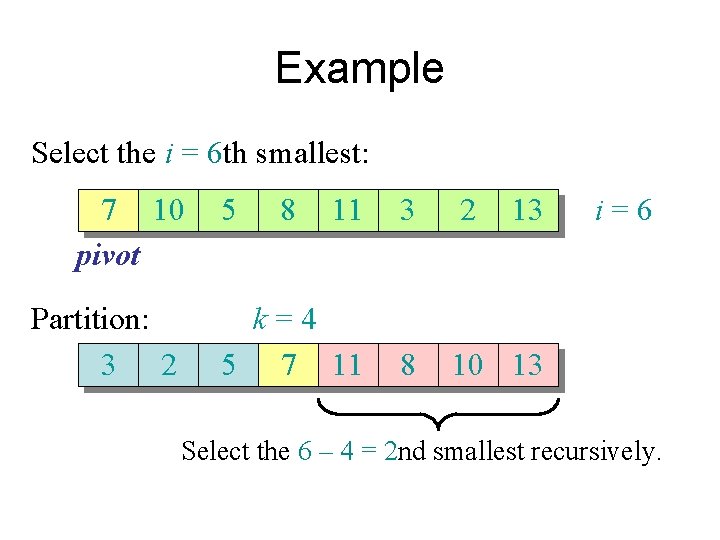
Example Select the i = 6 th smallest: 7 10 pivot Partition: 3 2 5 8 11 3 2 13 k=4 5 7 11 8 10 13 i=6 Select the 6 – 4 = 2 nd smallest recursively.

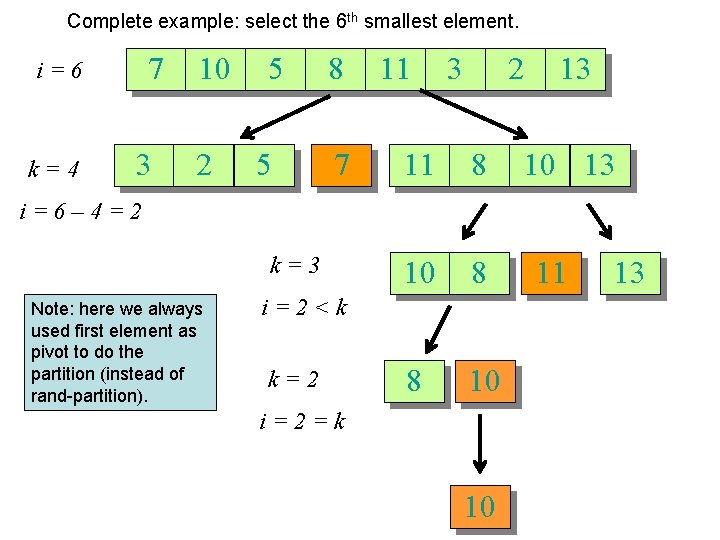
Complete example: select the 6 th smallest element. 7 i=6 k=4 3 10 2 5 5 8 7 11 3 2 11 8 10 8 8 10 13 i=6– 4=2 k=3 Note: here we always used first element as pivot to do the partition (instead of rand-partition). i=2<k k=2 i=2=k 10 11 13

Intuition for analysis (All our analyses today assume that all elements are distinct. ) Lucky: T(n) = T(9 n/10) + Q(n) CASE 3 = Q(n) Unlucky: T(n) = T(n – 1) + Q(n) arithmetic series = Q(n 2) Worse than sorting!

Running time of randomized selection T(n) ≤ T(max(0, n– 1)) + n T(max(1, n– 2)) + n M T(max(n– 1, 0)) + n if 0 : n– 1 split, if 1 : n– 2 split, if n– 1 : 0 split, • For upper bound, assume ith element always falls in larger side of partition • The expected running time is an average of all cases Expectation

Substitution method Want to show T(n) = O(n). So need to prove T(n) ≤ cn for n > n 0 Assume: T(k) ≤ ck for all k < n Therefore, T(n) = O(n) if c ≥ 4

Summary of randomized selection • Works fast: linear expected time. • Excellent algorithm in practice. • But, the worst case is very bad: Q(n 2). Q. Is there an algorithm that runs in linear time in the worst case? A. Yes, due to Blum, Floyd, Pratt, Rivest, and Tarjan [1973]. IDEA: Generate a good pivot recursively.

Worst-case linear-time selection SELECT(i, n) 1. Divide the n elements into groups of 5. Find the median of each 5 -element group by rote. 2. Recursively SELECT the median x of the ën/5û group medians to be the pivot. 3. Partition around the pivot x. Let k = rank(x). 4. if i = k then return x elseif i < k then recursively SELECT the i th smallest element in the lower part else recursively SELECT the (i–k)th smallest element in the upper part Same as RANDSELECT

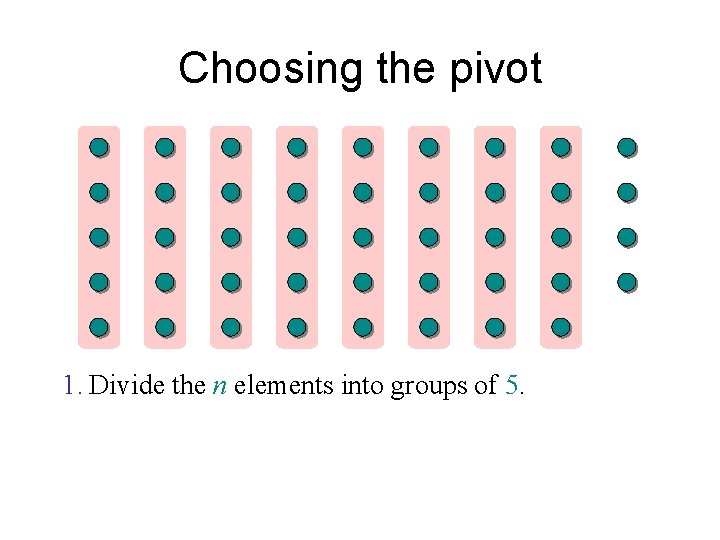
Choosing the pivot

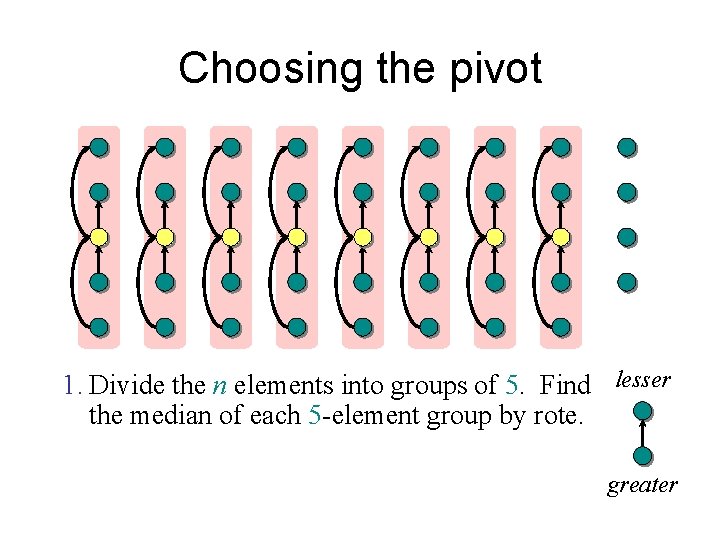
Choosing the pivot 1. Divide the n elements into groups of 5.

Choosing the pivot 1. Divide the n elements into groups of 5. Find lesser the median of each 5 -element group by rote. greater

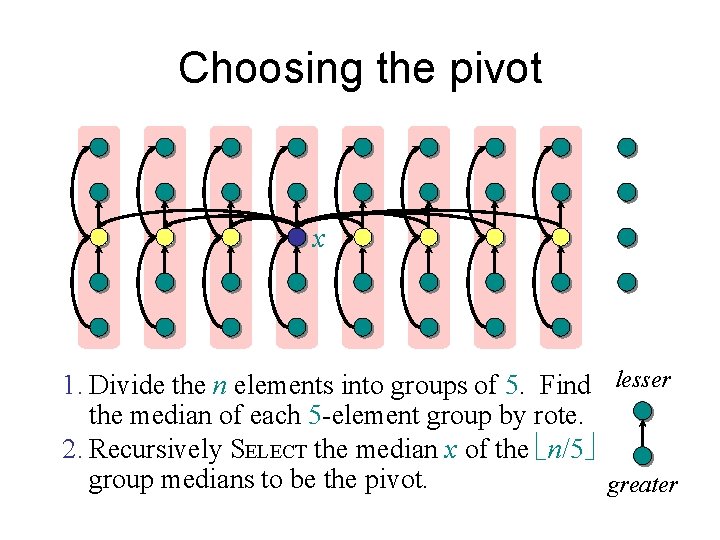
Choosing the pivot x 1. Divide the n elements into groups of 5. Find lesser the median of each 5 -element group by rote. 2. Recursively SELECT the median x of the ë n/5û group medians to be the pivot. greater

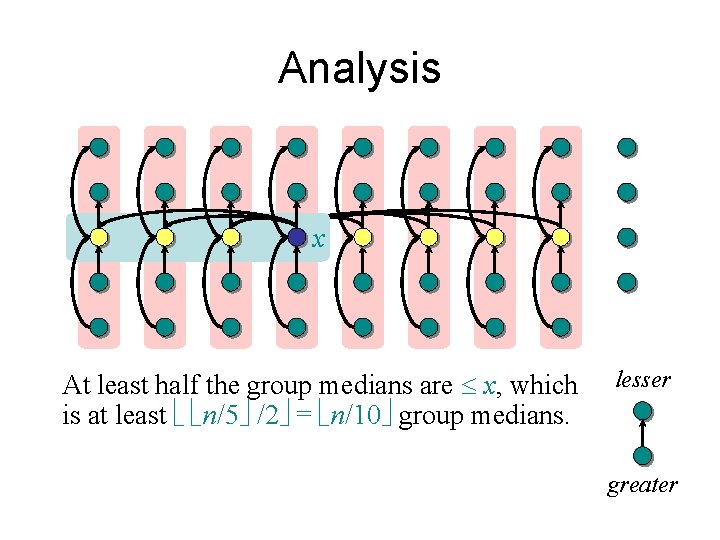
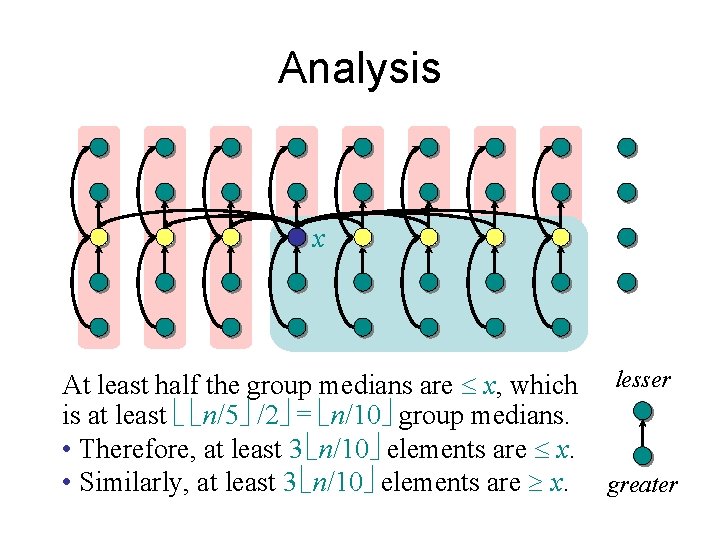
Analysis x At least half the group medians are x, which is at least ë ë n/5û /2û = ë n/10û group medians. lesser greater

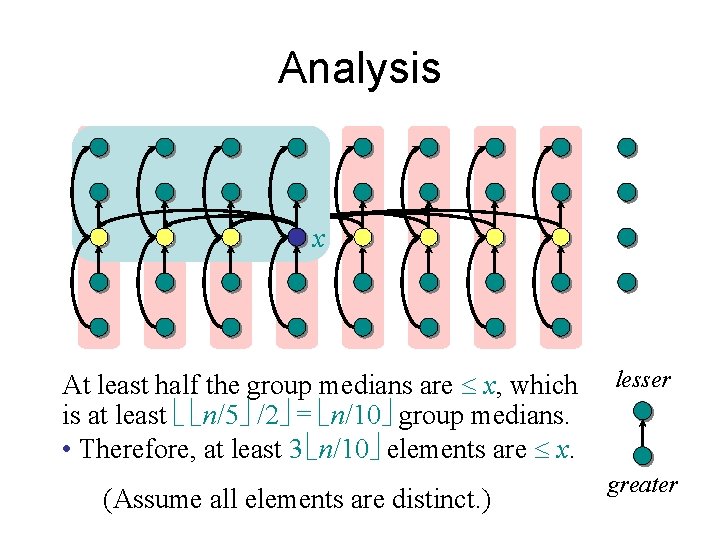
Analysis x At least half the group medians are x, which is at least ë ë n/5û /2û = ë n/10û group medians. • Therefore, at least 3 ë n/10û elements are x. (Assume all elements are distinct. ) lesser greater

Analysis x At least half the group medians are x, which is at least ë ë n/5û /2û = ë n/10û group medians. • Therefore, at least 3 ë n/10û elements are x. • Similarly, at least 3 ë n/10û elements are x. lesser greater

Analysis Need “at most” for worst-case runtime • At least 3 ë n/10û elements are x at most n-3 ë n/10û elements are x • The recursive call to SELECT in Step 4 is executed recursively on at most n-3 ë n/10û elements. 3 ë n/10û Possible position for pivot 3 ë n/10û

Analysis • Use fact that ë a/bû > a/b-1 • n-3 ë n/10û < n-3(n/10 -1) 7 n/10 + 3 3 n/4 if n ≥ 60 • The recursive call to SELECT in Step 4 is executed recursively on at most 7 n/10+3 elements.

Developing the recurrence T(n) Q(n) T(n/5) Q(n) T(7 n/10 +3) SELECT(i, n) 1. Divide the n elements into groups of 5. Find the median of each 5 -element group by rote. 2. Recursively SELECT the median x of the ën/5û group medians to be the pivot. 3. Partition around the pivot x. Let k = rank(x). 4. if i = k then return x elseif i < k then recursively SELECT the i th smallest element in the lower part else recursively SELECT the (i–k)th smallest element in the upper part

Solving the recurrence Assumption: T(k) ck for all k < n if n ≥ 60 if c ≥ 20 and n ≥ 60

Conclusions • Since the work at each level of recursion is basically a constant fraction (19/20) smaller, the work per level is a geometric series dominated by the linear work at the root. • In practice, this algorithm runs slowly, because the constant in front of n is large. • The randomized algorithm is far more practical. Exercise: Try to divide into groups of 3 or 7. Exercise: Think about an application in sorting.