CS 3343 Analysis of Algorithms Lecture 25 P


















![SAT is NP-complete • Fact: SAT NP • Theorem [Cook’ 71]: For any ∏’ SAT is NP-complete • Fact: SAT NP • Theorem [Cook’ 71]: For any ∏’](https://slidetodoc.com/presentation_image_h/8f73f6cc56069da81469ec89974755fd/image-24.jpg)




- Slides: 35

CS 3343: Analysis of Algorithms Lecture 25: P and NP

Have seen so far • Algorithms for various problems – Sorting, order statistics, LCS, scheduling, MST, shortest path, etc – Running times O(n 2) , O(n log n), O(nm), etc. – i. e. , polynomial in the input size – Those are called tractable problems • Can we solve all (or most of) interesting problems in polynomial time?

Example difficult problem • Traveling Salesperson Problem (TSP) – Input: undirected graph with lengths on edges – Output: shortest tour that visits each vertex exactly once – An optimization problem • Best known algorithm: O(n 2 n) time. • Intractable 2 5 10 8 9 6 4 9 11 3 5 7

Comparison of functions log 2 n n nlog 2 n n 2 n 3 2 n n! 10 3. 3 10 33 102 103 106 102 660 104 106 1030 10158 103 104 106 109 104 13 104 105 108 1012 105 17 105 106 1010 1015 106 20 106 107 1012 1018 11/23/2020 For a super computer that does 1 trillion operations per second, it will be longer than 1 billion years 4

Another difficult problem • Maximum Clique: – Input: undirected graph G=(V, E) – Output: largest subset C of V such that every pair of vertices in C has an edge between them – An optimization problem • Best known algorithm: O(n 2 n) time

What can we do ? • Spend more time designing algorithms for those problems – People tried for a few decades, no luck • Prove there is no polynomial time algorithm for those problems – Would be great – Seems really difficult

What else can we do ? • Show that those hard problems are essentially equivalent. i. e. , if we can solve one of them in polynomial time, then all others can be solved in polynomial time as well. • Works for at least 10 000 hard problems

The benefits of equivalence • Combines research efforts • If one problem has polynomial time solution, then all of them do • More realistically: Once an exponential lower bound is shown for one problem, it holds for all of them P 1 P 2 P 3

Summing up • If we show that a problem ∏ is equivalent to ten thousand other well studied problems without efficient algorithms, then we get a very strong evidence that ∏ is hard. • We need to: – Identify the class of problems of interest – Define the notion of equivalence – Prove the equivalence(s)

Classes of problems: P and NP • Implicitly, we mean decision problems: answer YES or NO – Other problems can be converted into decision problems – k-clique: is there a clique of size = k? • P is set of problems that can be solved in polynomial time • NP (nondeterministic polynomial time) is the set of problems that can be solved in polynomial time by a nondeterministic computer

Nondeterminism • Think of a non-deterministic computer as a computer that magically “guesses” a solution, then has to verify that it is correct – If a solution exists, computer always guesses it – One way to imagine it: a parallel computer that can freely spawn an infinite number of processes • Have one processor work on each possible solution • All processors attempt to verify that their solution works • If a processor finds it has a working solution – So: NP = problems verifiable in polynomial time

P and NP • P = problems that can be solved in polynomial time • NP = problems for which a solution can be verified in polynomial time • K-clique problem is in NP: – Easy to verify solution in polynomial time • Is sorting in NP? – Not a decision problem • Is sortedness in NP? – Yes. Easy to verify

P and NP • Is P = NP? – The biggest open problem in CS – Most suspect not – the Clay Mathematics Institute has offered a $1 million prize for the first proof NP P or P = NP?

NP-Complete Problems • We will see that NP-Complete problems are the “hardest” problems in NP: – If any one NP-Complete problem can be solved in polynomial time… – …then every NP-Complete problem can be solved in polynomial time… – …and in fact every problem in NP can be solved in polynomial time (which would show P = NP) – Thus: solve TSP in O(n 100) time, you’ve proved that P = NP. Retire rich & famous.

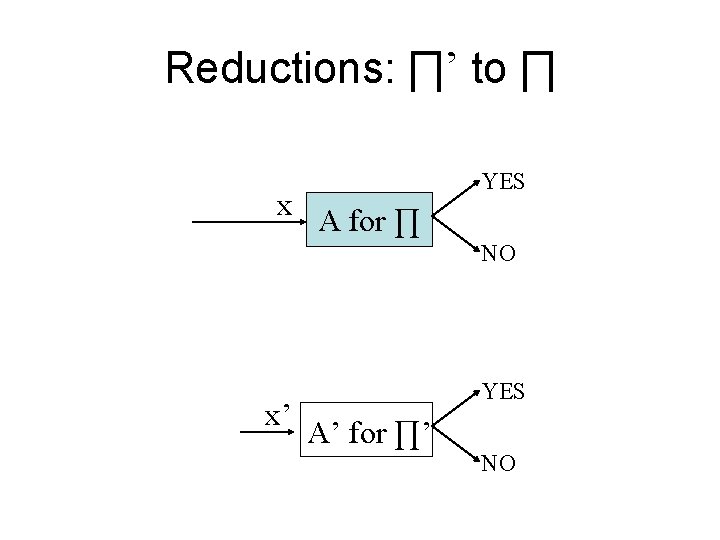
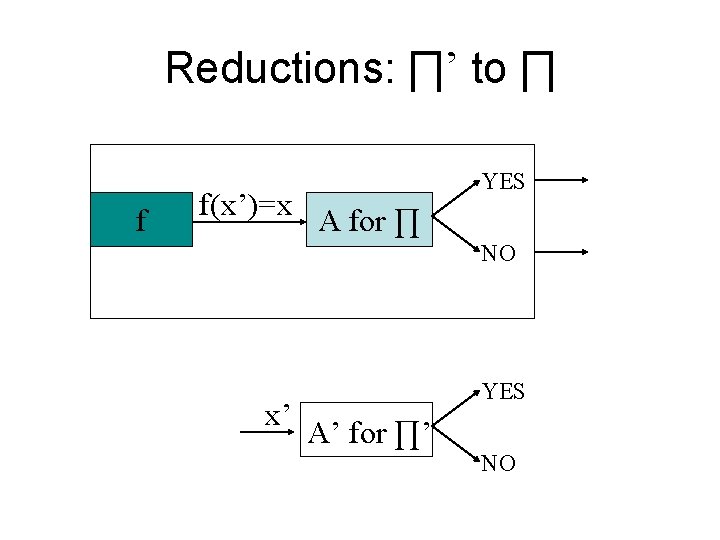
Reduction • The crux of NP-Completeness is reducibility – Informally, a problem ’ can be reduced to another problem if any instance of ’ can be “easily rephrased” as an instance of , the solution to which provides a solution to the instance of ’ • What do you suppose “easily” means? • This rephrasing is called transformation – Intuitively: If ’ reduces to , ’ is “no harder to solve” than

Reductions: ∏’ to ∏ x YES A for ∏ NO x’ YES A’ for ∏’ NO

Reductions: ∏’ to ∏ f f(x’)= x YES A for ∏ NO x’ YES A’ for ∏’ NO

Reduction: an example – ’: Given a set of Booleans, is at least one TRUE? – : Given a set of integers, is their sum positive? – Transformation: (x 1, x 2, …, xn) = (y 1, y 2, …, yn) where yi = 1 if xi = TRUE, yi = 0 if xi = FALSE

Reductions • ∏’ is polynomial time reducible to ∏ ( ∏’≤p ∏) iff there is a polynomial time function f that maps inputs x’ for ∏’ into inputs x for ∏, such that for any x’ ∏’(x’)=∏(f(x’)) • Fact 1: if ∏ P and ∏’ ≤p ∏ then ∏’ P • Fact 2: if ∏ NP and ∏’ ≤p ∏ then ∏’ NP • Fact 3 (transitivity): if ∏’’ ≤p ∏’ and ∏’ ≤p ∏ then ∏” ≤p ∏

Recap • We defined a large class of interesting problems, namely NP • We have a way of saying that one problem is not harder than another (∏’ ≤p ∏) • Our goal: show equivalence between hard problems

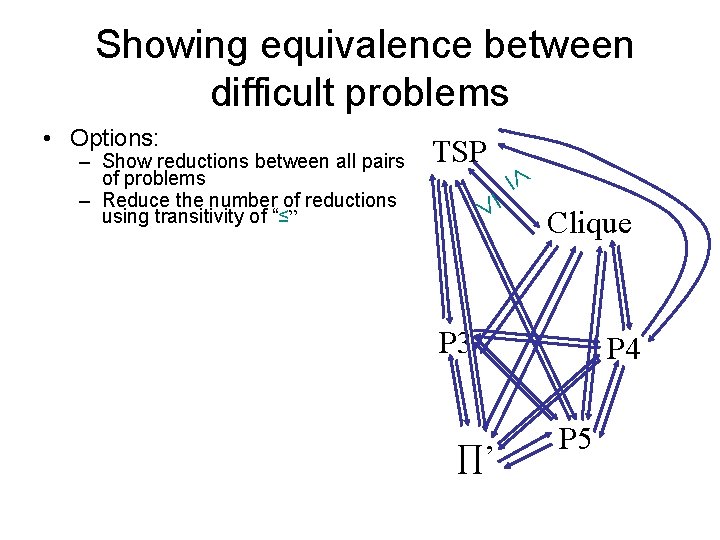
Showing equivalence between difficult problems TSP – Show reductions between all pairs of problems – Reduce the number of reductions using transitivity of “≤” • Options: Clique P 3 ∏’ P 4 P 5

Showing equivalence between difficult problems To show that some problem ∏’ NP is equivalent to all difficult problems, we only show ∏ ≤p ∏’. TSP – Show reductions between all pairs of problems – Reduce the number of reductions using transitivity of “≤” – Show that all problems in NP are reducible to a fixed ∏. Clique ∏ P 3 P 4 • Options: ∏’ P 5

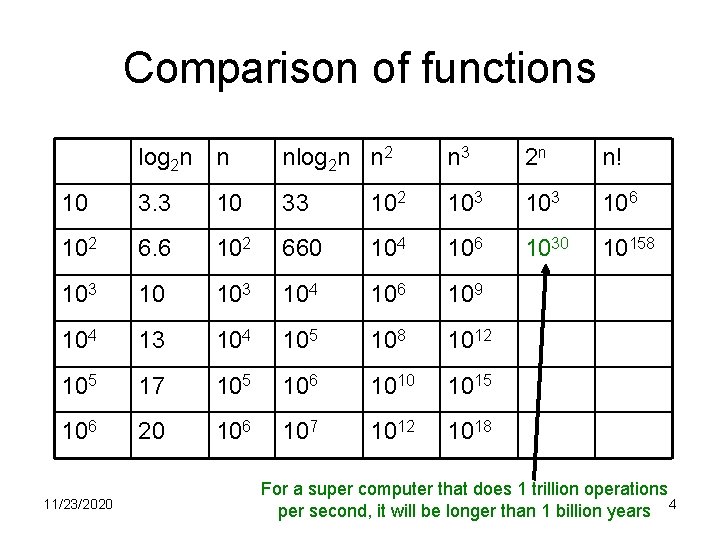
The first problem ∏ • Boolean satisfiability problem (SAT): – Given: a formula φ with m clauses over n variables, e. g. , x 1 v x 2 v x 5 , x 3 v ¬ x 5 – Check if there exists TRUE/FALSE assignments to the variables that makes the formula satisfiable • Any SAT can be rewritten into conjunctive normal form (CNF) – a conjunction of clauses, where a clause is a disjunction of literals • A literal is a Boolean variable or its negation – E. g. (A B) ( B C D) is in CNF (A B) ( A C D) is not in CNF
![SAT is NPcomplete Fact SAT NP Theorem Cook 71 For any SAT is NP-complete • Fact: SAT NP • Theorem [Cook’ 71]: For any ∏’](https://slidetodoc.com/presentation_image_h/8f73f6cc56069da81469ec89974755fd/image-24.jpg)
SAT is NP-complete • Fact: SAT NP • Theorem [Cook’ 71]: For any ∏’ NP , we have ∏’ ≤ SAT. • Definition: A problem ∏ such that for any ∏’ NP we have ∏’ ≤p ∏, is called NP-hard – Not necessarily decision problem • Definition: An NP-hard problem that belongs to NP is called NP-complete • Corollary: SAT is NP-complete.

• SAT: the boolean satisfiability problem formulas in conjunctive normal form • 0 -1 INTEGER PROGRAMMING • CLIQUE (see also independent set problem) Karp's 21 NP-complete • SET PACKING problems, 1972 • VERTEX COVER Since then thousands • SET COVERING problems have been • FEEDBACK NODE SET • FEEDBACK ARC SET proved to be NP • DIRECTED HAMILTONIAN CIRCUIT complete • UNDIRECTED HAMILTONIAN CIRCUIT • 3 -SAT • CHROMATIC NUMBER (also called the Graph Coloring Problem) • CLIQUE COVER • EXACT COVER • HITTING SET • STEINER TREE • 3 -dimensional MATCHING • KNAPSACK (Karp's definition of Knapsack is closer to Subset sum) • JOB SEQUENCING • PARTITION • MAX-CUT

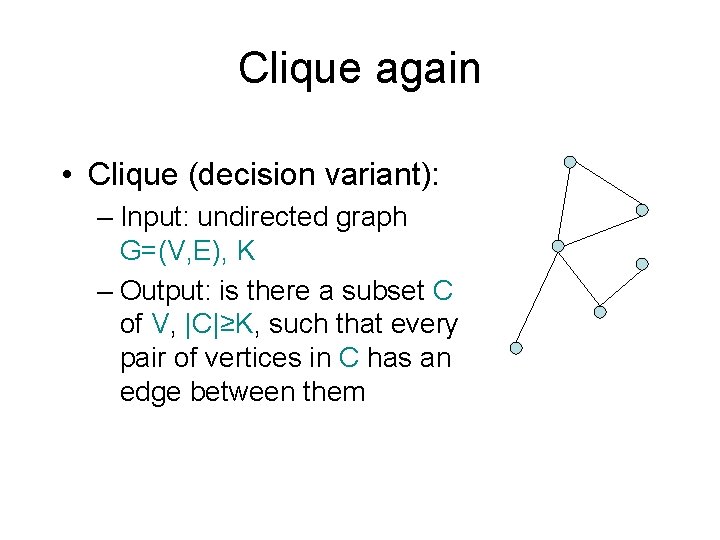
Clique again • Clique (decision variant): – Input: undirected graph G=(V, E), K – Output: is there a subset C of V, |C|≥K, such that every pair of vertices in C has an edge between them

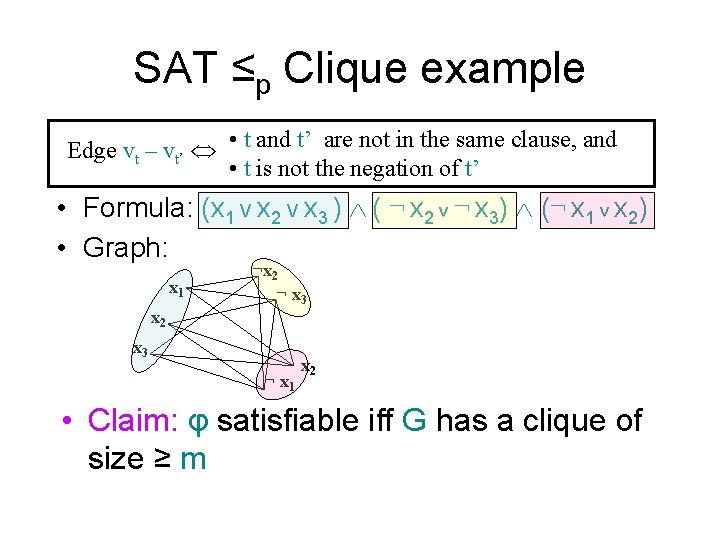
SAT ≤p Clique x’ • Given a SAT formula φ=C 1, …, Cm over x 1, …, xn, we need to produce G=(V, E) and K, f(x’)=x such that φ satisfiable iff G has a clique of size ≥ K.

SAT ≤p Clique reduction • For each literal t occurring in φ, create a vertex vt • Create an edge vt – vt’ iff: – t and t’ are not in the same clause, and – t is not the negation of t’

SAT ≤p Clique example Edge vt – vt’ • t and t’ are not in the same clause, and • t is not the negation of t’ • Formula: (x 1 V x 2 V x 3 ) ( ¬ x 2 v ¬ x 3) (¬ x 1 v x 2) • Graph: x 1 x 2 ¬ x 3 ¬ x 1 x 2 • Claim: φ satisfiable iff G has a clique of size ≥ m

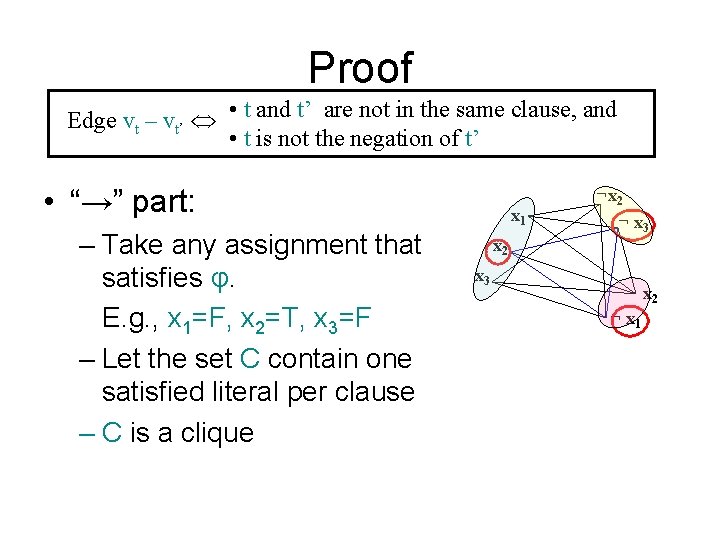
Proof Edge vt – vt’ • t and t’ are not in the same clause, and • t is not the negation of t’ • “→” part: – Take any assignment that satisfies φ. E. g. , x 1=F, x 2=T, x 3=F – Let the set C contain one satisfied literal per clause – C is a clique x 1 x 2 ¬ x 3 x 2 ¬ x 1

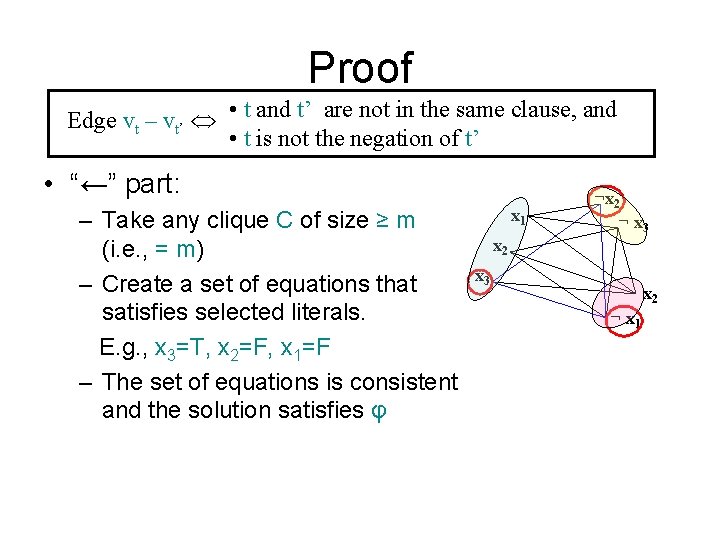
Proof Edge vt – vt’ • t and t’ are not in the same clause, and • t is not the negation of t’ • “←” part: – Take any clique C of size ≥ m (i. e. , = m) – Create a set of equations that satisfies selected literals. E. g. , x 3=T, x 2=F, x 1=F – The set of equations is consistent and the solution satisfies φ x 1 x 2 ¬ x 3 x 2 ¬ x 1

Altogether • We constructed a reduction that maps: – YES inputs to SAT to YES inputs to Clique – NO inputs to SAT to NO inputs to Clique • The reduction works in polynomial time • Therefore, SAT ≤p Clique →Clique NPhard • Clique is in NP → Clique is NP-complete

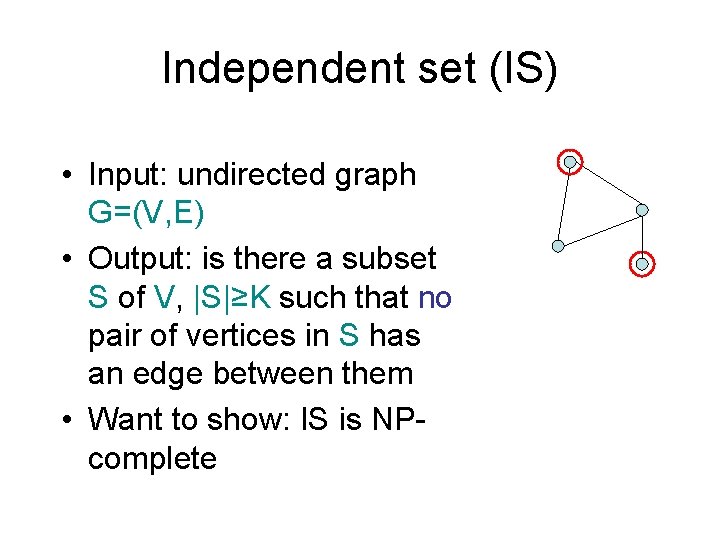
Independent set (IS) • Input: undirected graph G=(V, E) • Output: is there a subset S of V, |S|≥K such that no pair of vertices in S has an edge between them • Want to show: IS is NPcomplete

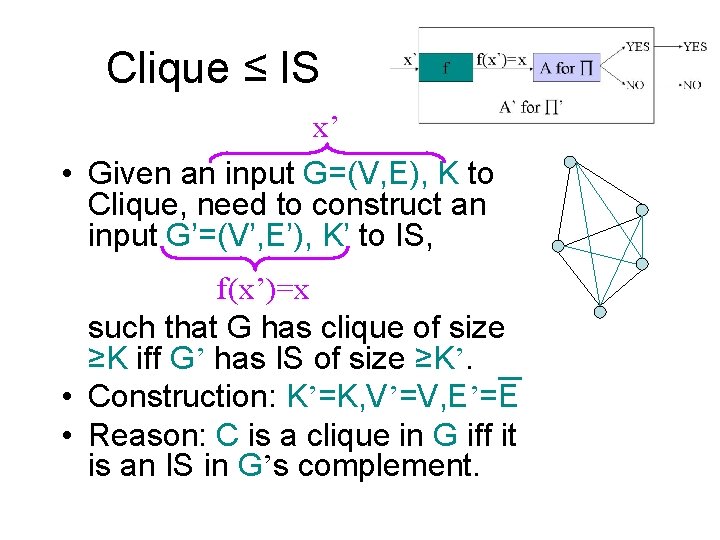
Clique ≤ IS x’ • Given an input G=(V, E), K to Clique, need to construct an input G’=(V’, E’), K’ to IS, f(x’)=x such that G has clique of size ≥K iff G’ has IS of size ≥K’. • Construction: K’=K, V’=V, E’=E • Reason: C is a clique in G iff it is an IS in G’s complement.

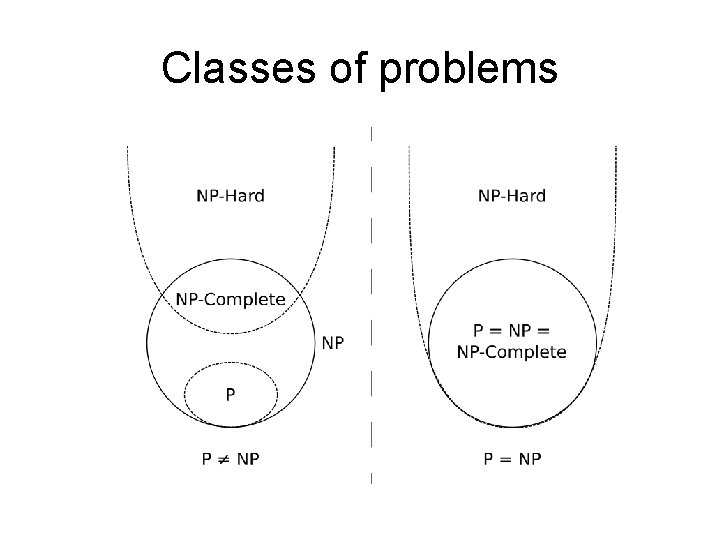
Classes of problems