Corso di Teoria dei Giochi Laurea specialistica in

Corso di Teoria dei Giochi Laurea specialistica in Economia Applicata Docente: Giovanni D’Orio E-mail: giovanni. dorio@unical. it Giochi dinamici ad informazione completa Teoria dei giochi - D'Orio - seconda parte 1

Panoramica dei giochi dinamici ad informazione completa Giochi dinamici ad informazione completa Rappresentazione in forma estensiva (o estesa) Giochi dinamici ad informazione completa e perfetta Albero del gioco Equilibrio di Nash perfetto nei sottogiochi Backward induction (Induzione all’indietro) Applicazioni Giochi dinamici ad informazione completa ed imperfetta n Altre applicazioni n Giochi ripetuti n n n n Teoria dei giochi - D'Orio - seconda parte 2

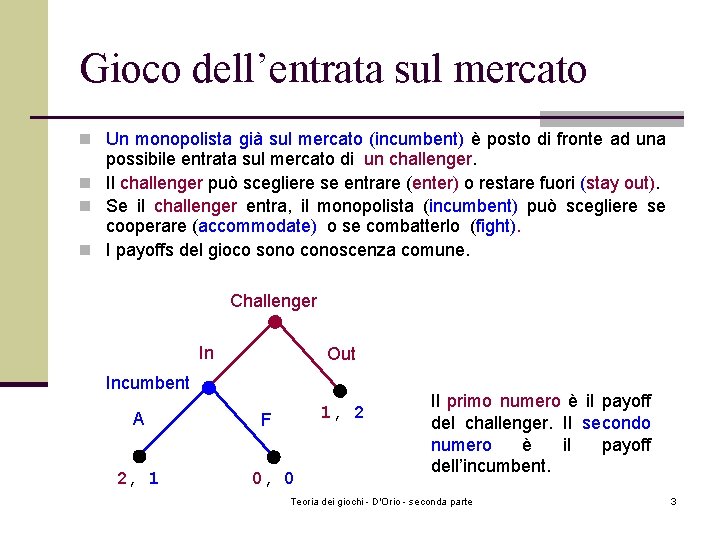
Gioco dell’entrata sul mercato n Un monopolista già sul mercato (incumbent) è posto di fronte ad una possibile entrata sul mercato di un challenger. n Il challenger può scegliere se entrare (enter) o restare fuori (stay out). n Se il challenger entra, il monopolista (incumbent) può scegliere se cooperare (accommodate) o se combatterlo (fight). n I payoffs del gioco sono conoscenza comune. Challenger In Out Incumbent A 2, 1 1, 2 F 0, 0 Il primo numero è il payoff del challenger. Il secondo numero è il payoff dell’incumbent. Teoria dei giochi - D'Orio - seconda parte 3

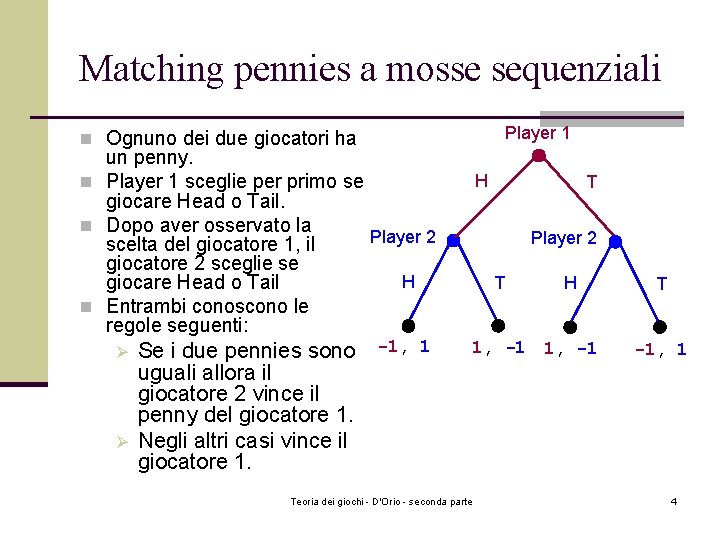
Matching pennies a mosse sequenziali Player 1 n Ognuno dei due giocatori ha un penny. n Player 1 sceglie per primo se giocare Head o Tail. n Dopo aver osservato la Player 2 scelta del giocatore 1, il giocatore 2 sceglie se H giocare Head o Tail n Entrambi conoscono le regole seguenti: Ø Ø Se i due pennies sono -1, 1 uguali allora il giocatore 2 vince il penny del giocatore 1. Negli altri casi vince il giocatore 1. H T Player 2 T H 1, -1 Teoria dei giochi - D'Orio - seconda parte T -1, 1 4

Giochi dinamici ad informazione perfetta (o a mosse sequenziali) n Un insieme di giocatori n Chi muove quando e quali scelte sono disponibili? n Cosa sanno i giocatori quando muovono? n I payoff dei giocatori sono determinati dalle proprie scelte. n Tutte le scelte possibili sono conoscenza comune dei due giocatori. Teoria dei giochi - D'Orio - seconda parte 5

Definizione: rappresentazione in forma estensiva (o estesa) n La forma estesa di un gioco specifica: Ø I giocatori del gioco Ø Quando ogni giocatore deve muovere Ø Cosa può fare ogni giocatore quando è il suo turno Ø Cosa conosce ogni giocatore quando è il suo turno Ø il payoff ricevuto da ogni giocatore per ogni combinazione mosse che potrebbe essere scelta dai giocatori Teoria dei giochi - D'Orio - seconda parte 6

Giochi dinamici ad informazione completa e perfetta n Informazione perfetta Ø Tutte le mosse precedenti sono osservabili prima che venga scelta la prossima mossa. Ø Un giocatore sa Chi ha mosso e Cosa ha fatto prima che esso prenda una decisione Teoria dei giochi - D'Orio - seconda parte 7

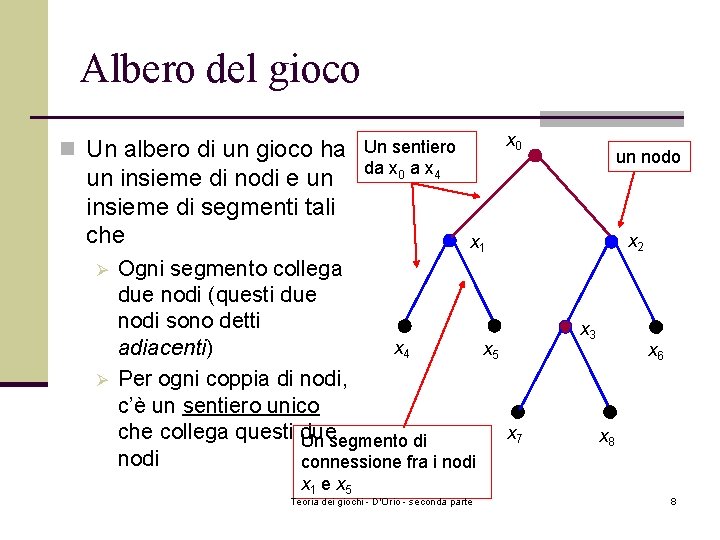
Albero del gioco x 0 n Un albero di un gioco ha Un sentiero un insieme di nodi e un insieme di segmenti tali che Ø Ø x 2 x 1 Ogni segmento collega due nodi (questi due nodi sono detti x 4 adiacenti) x 5 Per ogni coppia di nodi, c’è un sentiero unico x 7 che collega questi due Un segmento di nodi connessione fra i nodi x 1 e x 5 un nodo da x 0 a x 4 Teoria dei giochi - D'Orio - seconda parte x 3 x 6 x 8 8

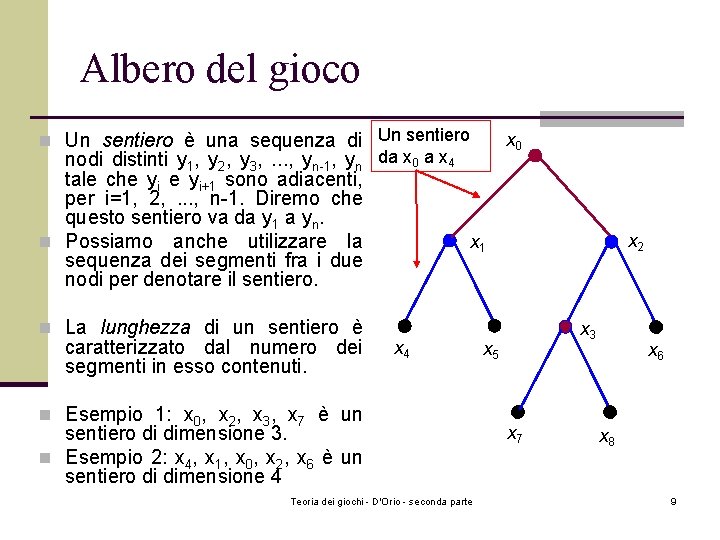
Albero del gioco n Un sentiero è una sequenza di Un sentiero nodi distinti y 1, y 2, y 3, . . . , yn-1, yn da x 0 a x 4 tale che yi+1 sono adiacenti, per i=1, 2, . . . , n-1. Diremo che questo sentiero va da y 1 a yn. n Possiamo anche utilizzare la sequenza dei segmenti fra i due nodi per denotare il sentiero. n La lunghezza di un sentiero è caratterizzato dal numero dei segmenti in esso contenuti. x 0 x 2 x 1 x 4 n Esempio 1: x 0, x 2, x 3, x 7 è un sentiero di dimensione 3. n Esempio 2: x 4, x 1, x 0, x 2, x 6 è un sentiero di dimensione 4 Teoria dei giochi - D'Orio - seconda parte x 3 x 5 x 7 x 6 x 8 9

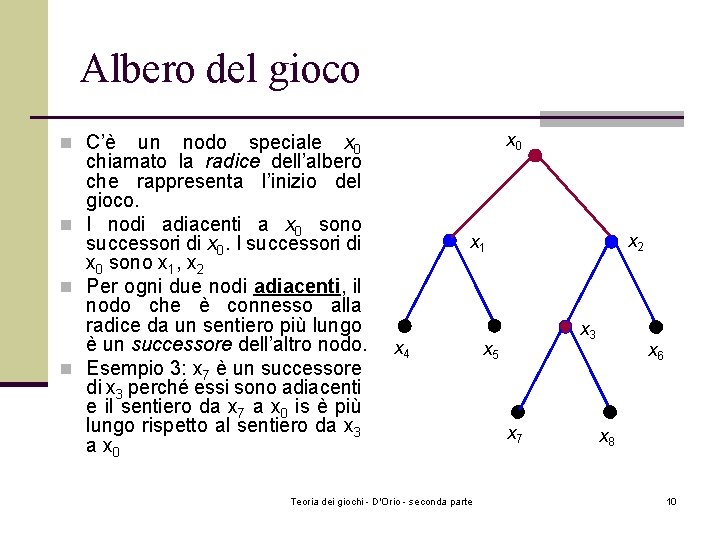
Albero del gioco un nodo speciale x 0 chiamato la radice dell’albero che rappresenta l’inizio del gioco. n I nodi adiacenti a x 0 sono successori di x 0. I successori di x 0 sono x 1, x 2 n Per ogni due nodi adiacenti, il nodo che è connesso alla radice da un sentiero più lungo è un successore dell’altro nodo. n Esempio 3: x 7 è un successore di x 3 perché essi sono adiacenti e il sentiero da x 7 a x 0 is è più lungo rispetto al sentiero da x 3 a x 0 n C’è x 2 x 1 x 4 Teoria dei giochi - D'Orio - seconda parte x 3 x 5 x 7 x 6 x 8 10

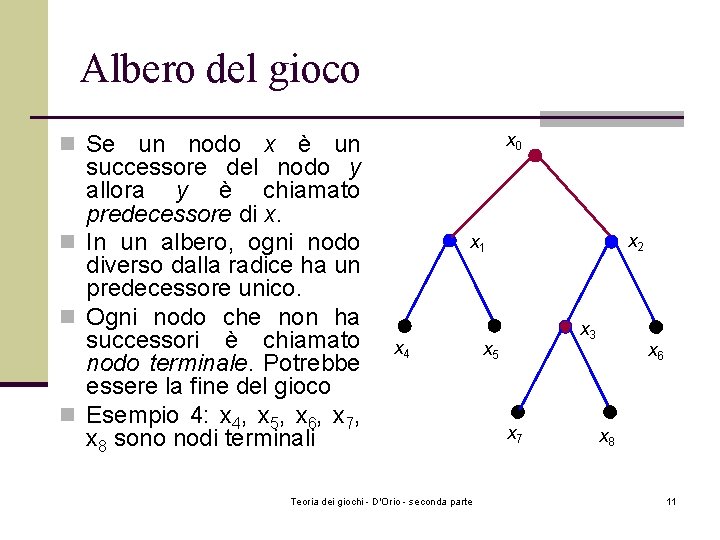
Albero del gioco un nodo x è un successore del nodo y allora y è chiamato predecessore di x. n In un albero, ogni nodo diverso dalla radice ha un predecessore unico. n Ogni nodo che non ha successori è chiamato nodo terminale. Potrebbe essere la fine del gioco n Esempio 4: x 4, x 5, x 6, x 7, x 8 sono nodi terminali x 0 n Se x 2 x 1 x 4 Teoria dei giochi - D'Orio - seconda parte x 3 x 5 x 7 x 6 x 8 11

Albero del gioco Player 1 n Ogni nodo diverso dai nodi terminali rappresenta qualche giocatore. n Per un nodo diverso da un terminale, I segmenti che lo collegano con i successori rappresentano le azioni disponibili per il giocatore rappresentato in quel nodo. H T Player 2 H -1, 1 T H 1, -1 Teoria dei giochi - D'Orio - seconda parte T -1, 1 12

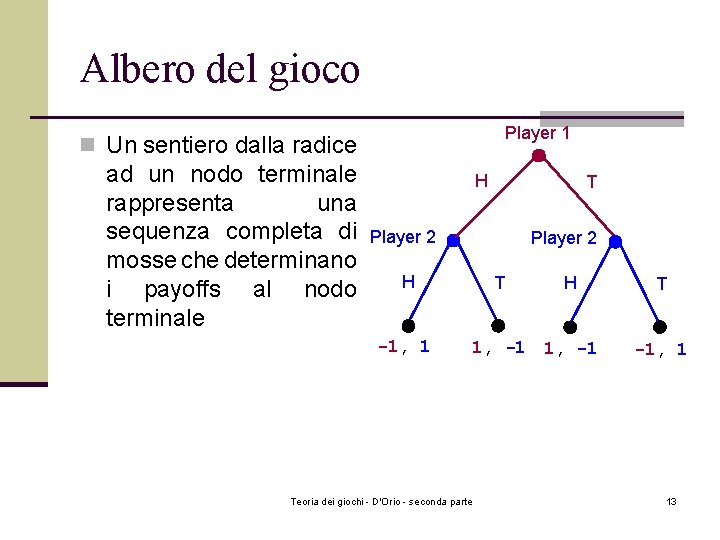
Albero del gioco Player 1 n Un sentiero dalla radice ad un nodo terminale rappresenta una sequenza completa di mosse che determinano i payoffs al nodo terminale H T Player 2 H -1, 1 T H 1, -1 Teoria dei giochi - D'Orio - seconda parte T -1, 1 13

Strategia n La strategia di un giocatore è un piano di azioni completo. n La strategia (o il piano completo di azioni) specifica una azione possibile per il giocatore in qualsiasi contingenza esso potrebbe essere chiamato in azione. Teoria dei giochi - D'Orio - seconda parte 14

Gioco dell’entrata nel mercato n Strategie del Challenger Ø Ø In Out n Strategie dell’Incumbent Ø Ø Accommodate (se il challenger gioca In) Fight (se il challenger gioca In) n Payoffs n Rappresentazione in forma Normale Incumbent Accommodate Challenger Fight In 2 , 1 0 , 0 Out 1 , 2 Teoria dei giochi - D'Orio - seconda parte 15

Strategie e payoff n In un albero, la strategia di un giocatore è rappresentata da un insieme di segmenti. n Una combinazione di strategie (insiemi dei segmenti), una per ogni giocatore, sviluppa un sentiero dalla radice al nodo terminale, il quale determina i payoffs di tutti i giocatori. Teoria dei giochi - D'Orio - seconda parte 16

Matching pennies a mosse sequenziali n Strategie del giocatore 1 Ø Head Ø Tail n Strategie del giocatore 2 Ø H se player 1 gioca H, H se player 1 gioca T Ø H se player 1 gioca H, T se player 1 gioca T Ø T se player 1 gioca H, H se player 1 gioca T Ø T se player 1 gioca H, T se player 1 gioca T Le strategie del giocatore 2 sono denotate rispettivamente da HH, HT, TH e TT. Teoria dei giochi - D'Orio - seconda parte 17

Matching pennies a mosse sequenziali n I payoffs n Rappresentazione in forma Normale Player 2 Player 1 H HH -1 , 1 T 1 , -1 HT -1 , 1 TH 1 , -1 -1 , -1 1 Teoria dei giochi - D'Orio - seconda parte TT 1 , -1 -1 , 1 18

Equilibrio di Nash n L’insieme degli equilibri di Nash in un gioco dinamico ad informazione completa è l’insieme degli equilibri di Nash nella sua forma normale. n Come trovare l’equilibrio di Nash in un gioco dinamico ad informazione completa Costruite la forma normale del gioco dinamico ad informazione completa Ø Trovate l’equilibrio di Nash nella forma normale. Ø Teoria dei giochi - D'Orio - seconda parte 19

Equilibrio di Nash nel gioco dell’entrata nel mercato n Due equilibri di Nash Ø ( In, Accommodate ) Ø ( Out, Fight ) n Ha senso considerare il secondo equilibrio ( Out, Fight )? n Minacce non credibili Incumbent Accommodate Challenger Fight In 2 , 1 0 , 0 Out 1 , 2 Teoria dei giochi - D'Orio - seconda parte 20

Rimozione degli equilibri di Nash non ragionevole n L’equilibrio di Nash perfetto nei sottogiochi è una “raffinazione” dell’equilibrio di Nash n Questo processo di “refinement” può eliminare equilibri di Nash non ragionevoli oppure minacce non credibili Teoria dei giochi - D'Orio - seconda parte 21

Riassunto n Giochi dinamici ad informazione completa e perfetta n Rappresentazione dei giochi in forma estesa n Albero del gioco n Prossimo argomento n Sottogioco n Equilibrio di Nash perfetto nei sottogiochi n Backward induction (induzione all’indietro) Teoria dei giochi - D'Orio - seconda parte 22

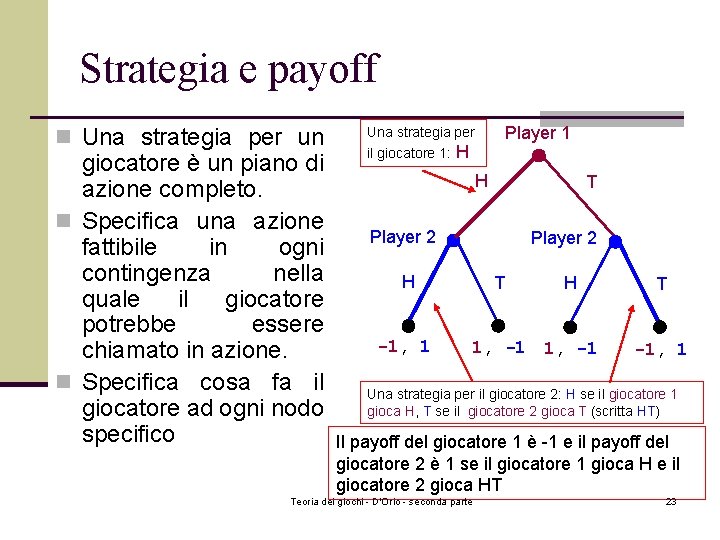
Strategia e payoff n Una strategia per un giocatore è un piano di azione completo. n Specifica una azione fattibile in ogni contingenza nella quale il giocatore potrebbe essere chiamato in azione. n Specifica cosa fa il giocatore ad ogni nodo specifico Una strategia per il giocatore 1: H Player 1 H T Player 2 H -1, 1 T H 1, -1 T -1, 1 Una strategia per il giocatore 2: H se il giocatore 1 gioca H, T se il giocatore 2 gioca T (scritta HT) Il payoff del giocatore 1 è -1 e il payoff del giocatore 2 è 1 se il giocatore 1 gioca H e il giocatore 2 gioca HT Teoria dei giochi - D'Orio - seconda parte 23

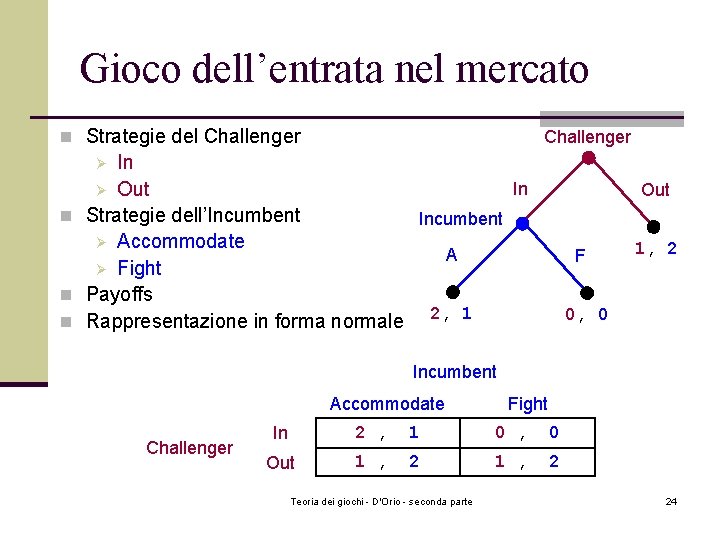
Gioco dell’entrata nel mercato n Strategie del Challenger In In Ø Out n Strategie dell’Incumbent Ø Accommodate A Ø Fight n Payoffs n Rappresentazione in forma normale 2, 1 Ø Out F 1, 2 0, 0 Incumbent Accommodate Challenger Fight In 2 , 1 0 , 0 Out 1 , 2 Teoria dei giochi - D'Orio - seconda parte 24

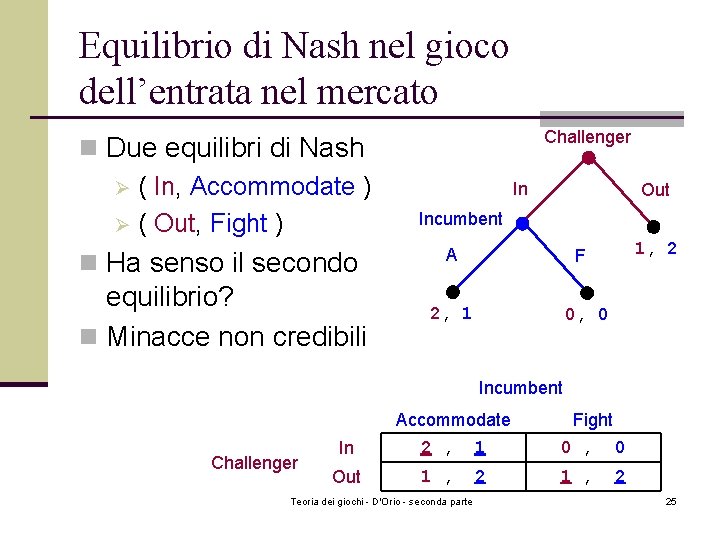
Equilibrio di Nash nel gioco dell’entrata nel mercato n Due equilibri di Nash Ø ( In, Accommodate ) Ø ( Out, Fight ) Challenger In Out Incumbent n Ha senso il secondo A equilibrio? n Minacce non credibili 2, 1 1, 2 F 0, 0 Incumbent Accommodate Challenger Fight In 2 , 1 0 , 0 Out 1 , 2 Teoria dei giochi - D'Orio - seconda parte 25

Rimozione degli NE non credibili n SNE (equilibrio di Nash nei sottogiochi) è un equilibrio di Nash “raffinato” n Può eliminare NE che non hanno senso o minacce non credibili n Dobbiamo però definire prima i sottogiochi Teoria dei giochi - D'Orio - seconda parte 26

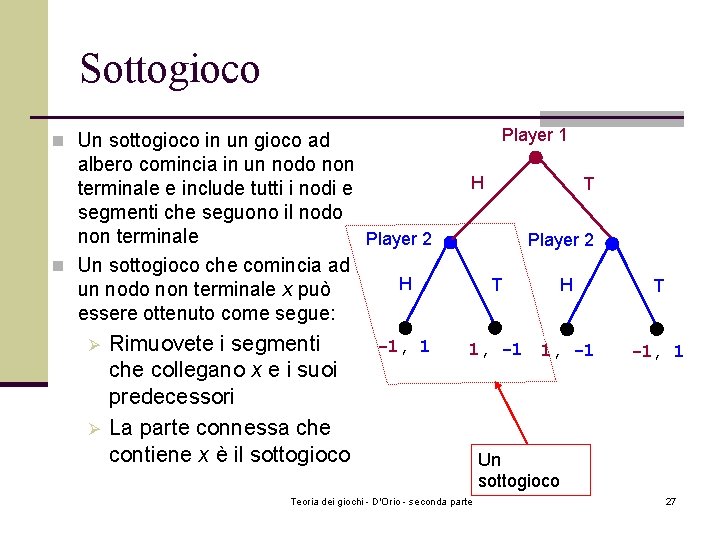
Sottogioco Player 1 n Un sottogioco in un gioco ad albero comincia in un nodo non terminale e include tutti i nodi e segmenti che seguono il nodo non terminale Player 2 n Un sottogioco che comincia ad H un nodo non terminale x può essere ottenuto come segue: Ø Ø Rimuovete i segmenti che collegano x e i suoi predecessori La parte connessa che contiene x è il sottogioco -1, 1 H T Player 2 T H 1, -1 Teoria dei giochi - D'Orio - seconda parte T -1, 1 Un sottogioco 27

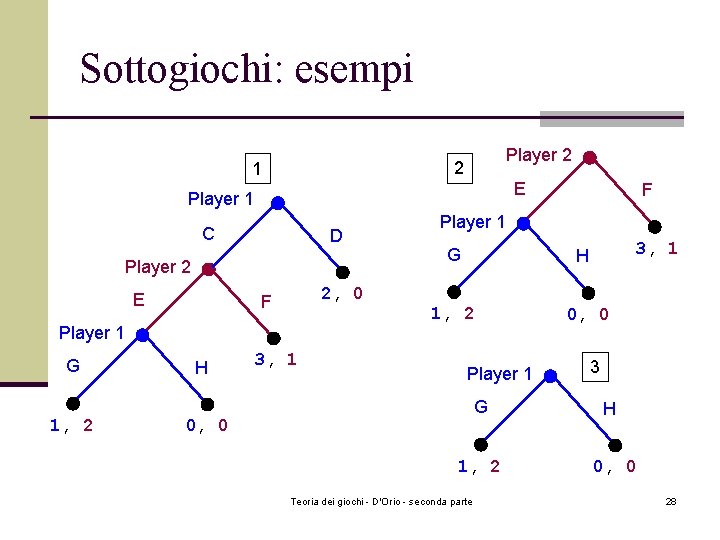
Sottogiochi: esempi Player 2 2 1 E Player 1 C D Player 2 E 2, 0 F Player 1 G 1, 2 H 3, 1 F Player 1 G 3, 1 H 1, 2 Player 1 G 0, 0 1, 2 Teoria dei giochi - D'Orio - seconda parte 0, 0 3 H 0, 0 28

Equilibrio di Nash perfetto nei sottogiochi (SNE) n Un equilibrio di Nash equilibrium of a dynamic gadi un gioco dinamico è perfetto nei sottogiochi se le strategie del NE costituiscono un NE in ogni sottogioco del gioco stesso. n SNE è un NE. Teoria dei giochi - D'Orio - seconda parte 29

Gioco dell’entrata nel mercato n Due equilibri di Nash Ø ( In, Accommodate ) è un SNE. Ø ( Out, Fight ) non è un SNE perché non costituisce un NE nel sottogioco che comincia dall’Incumbent. Challenger Incumbent In Out A 1, 2 2, 1 F Incumbent A 2, 1 F 0, 0 Accommodate è il NE di questo sottogioco. Teoria dei giochi - D'Orio - seconda parte 30

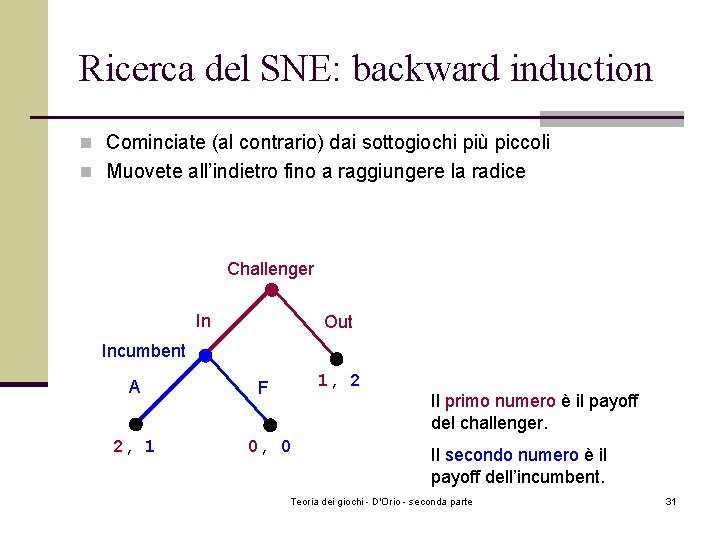
Ricerca del SNE: backward induction n Cominciate (al contrario) dai sottogiochi più piccoli n Muovete all’indietro fino a raggiungere la radice Challenger In Out Incumbent A 2, 1 1, 2 F Il primo numero è il payoff del challenger. 0, 0 Il secondo numero è il payoff dell’incumbent. Teoria dei giochi - D'Orio - seconda parte 31

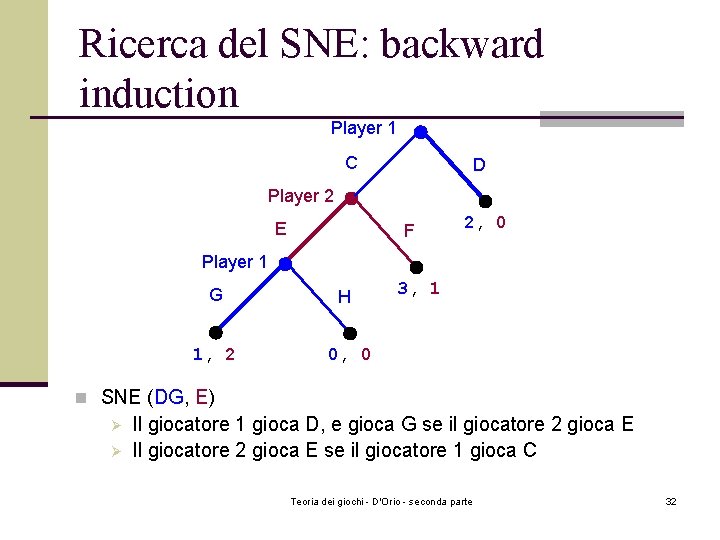
Ricerca del SNE: backward induction Player 1 C D Player 2 E F 2, 0 Player 1 G 1, 2 H 3, 1 0, 0 n SNE (DG, E) Ø Ø Il giocatore 1 gioca D, e gioca G se il giocatore 2 gioca E Il giocatore 2 gioca E se il giocatore 1 gioca C Teoria dei giochi - D'Orio - seconda parte 32

Esistenza del SNE n Ogni gioco dinamico finito ad informazione perfetta e completa ha un SNE che può essere ricavato per backward induction. Teoria dei giochi - D'Orio - seconda parte 33

Contrattazione sequenziale (2. 1. D del Gibbons) n I giocatori 1 e 2 stanno contrattando su un dollaro. La sequenza n n n è come segue: All’inizio del primo periodo, il giocatore 1 propone di prendere una quota s 1 del dollaro, lasciando 1 -s 1 al giocatore 2. Il giocatore 2 o accetta l’offerta o la rifiuta (in questo caso il gioco passa al secondo stadio) All’inizio del secondo stadio, il giocatore 2 propone al giocatore 1 di prendersi una quota s 2 del dollaro, lasciando 1 -s 2 al giocatore 2. Il giocatore 1 o accetta l’offerta o la rifiuta (in questo caso il gioco passa al terzo stadio) All’inizio del terzo periodo, il giocatore 1 riceve una quota s del dollaro, lasciando 1 -s al giocatore 2, dove 0<s <1. I giocatori sono impazienti. Essi scontano i payoff di un tasso di sconto pari a , dove 0< <1 Teoria dei giochi - D'Orio - seconda parte 34

Contrattazione sequenziale (2. 1. D del Gibbons) Player 1 propone un’offerta ( s 1 , 1 -s 1 ) Periodo 1 Player 2 accetta s 1 , 1 -s 1 rifiuta Player 2 Periodo 2 Propone un’offerta ( s 2 , 1 -s 2 ) Player 1 accetta s 2 , 1 -s 2 rifiuta Periodo 3 s , 1 -s Teoria dei giochi - D'Orio - seconda parte 35

Soluzione del gioco di contrattazione con la backward induction n Periodo 2: Ø Il giocatore 1 accetta s 2 se e solo se s 2 s. (assumiamo che l’offerta verrà accettata se si è indifferenti) Ø Il giocatore 2 si trova di fronte a queste due opzioni: (1) offre s 2 = s al giocatore 1, lasciando 1 -s 2 = 1 - s per se stesso a questo periodo, oppure (2) offre s 2 < s al giocatore 1 (e il giocatore 1 rifiuterà), e riceve 1 -s al prossimo periodo. Il calore scontato di questa somma è (1 -s) Ø Dato che (1 -s)<1 - s, il giocatore 2 dovrebbe proporre un’offerta (s 2* , 1 -s 2* ), dove s 2* = s. Il giocatore 1 la accetterà. Teoria dei giochi - D'Orio - seconda parte 36

Contrattazione sequenziale (2. 1. D del Gibbons) Player 1 propone un offerta ( s 1 , 1 -s 1 ) Periodo 1 Player 2 accetta rifiuta Player 2 Periodo 2 s 1 , 1 -s 1 s , 1 - s Propone un’offerta ( s 2 , 1 -s 2 ) Player 1 accetta s 2 , 1 -s 2 rifiuta Periodo 3 s , 1 -s Teoria dei giochi - D'Orio - seconda parte 37

Soluzione del gioco di contrattazione con la backward induction n Periodo 1: Ø Il giocatore 2 accetta 1 -s 1 se e solo se 1 -s 1 (1 -s 2*)= (1 - s) o s 1 1 - (1 -s 2*), dove s 2* = s. Ø Il giocatore 1 ha due opzioni: (1) offre 1 -s 1 = (1 -s 2*)= (1 - s) al giocatore 2, tenendosi s 1 = 1 - (1 -s 2*)=1 - + s per se stesso in questo periodo, oppure (2) offre 1 -s 1 < (1 -s 2*) al giocatore 2 (il giocatore 2 rifiuterà), e riceve s 2* = s il prossimo periodo. Il suo valore scontato sarà però s Ø Dato che s < 1 - + s, il giocatore 1 dovrà proporre un’offerta (s 1* , 1 -s 1* ), dove s 1* = 1 - + s Teoria dei giochi - D'Orio - seconda parte 38

Riassunto n SNE n Backward induction n Prossimo argomento n Il Modello del duopolio di Stackelberg n Salari e occupazione in una impresa sindacalizzata Teoria dei giochi - D'Orio - seconda parte 39

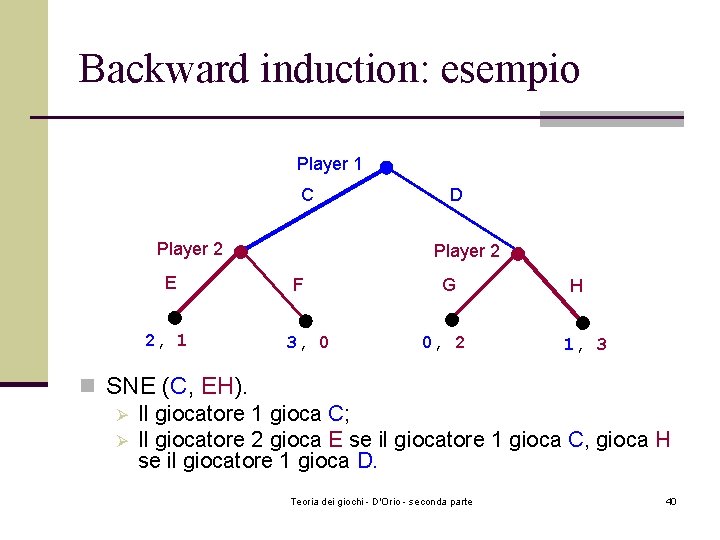
Backward induction: esempio Player 1 C Player 2 E 2, 1 D Player 2 F 3, 0 G 0, 2 H 1, 3 n SNE (C, EH). Ø Il giocatore 1 gioca C; Ø Il giocatore 2 gioca E se il giocatore 1 gioca C, gioca H se il giocatore 1 gioca D. Teoria dei giochi - D'Orio - seconda parte 40

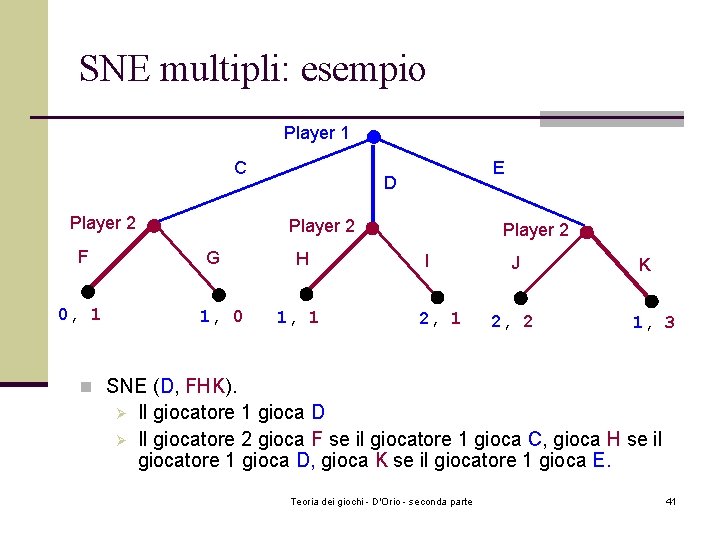
SNE multipli: esempio Player 1 C Player 2 F D Player 2 G 0, 1 E 1, 0 H 1, 1 Player 2 I 2, 1 J 2, 2 K 1, 3 n SNE (D, FHK). Ø Ø Il giocatore 1 gioca D Il giocatore 2 gioca F se il giocatore 1 gioca C, gioca H se il giocatore 1 gioca D, gioca K se il giocatore 1 gioca E. Teoria dei giochi - D'Orio - seconda parte 41

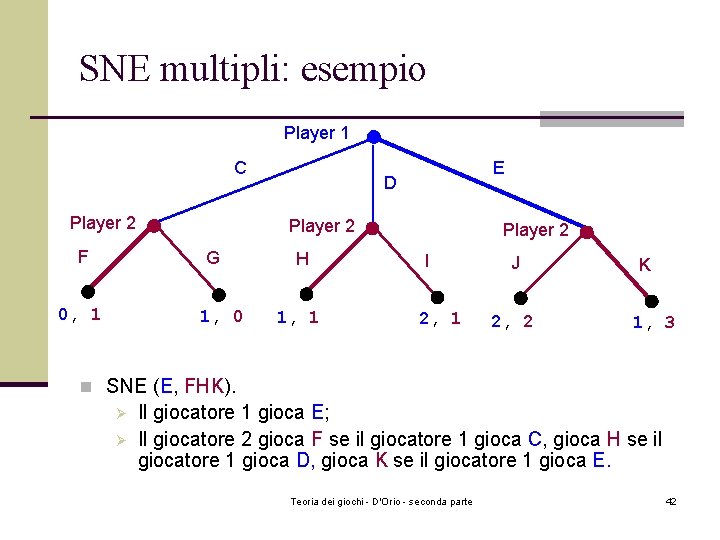
SNE multipli: esempio Player 1 C Player 2 F D Player 2 G 0, 1 E 1, 0 H 1, 1 Player 2 I 2, 1 J 2, 2 K 1, 3 n SNE (E, FHK). Ø Ø Il giocatore 1 gioca E; Il giocatore 2 gioca F se il giocatore 1 gioca C, gioca H se il giocatore 1 gioca D, gioca K se il giocatore 1 gioca E. Teoria dei giochi - D'Orio - seconda parte 42

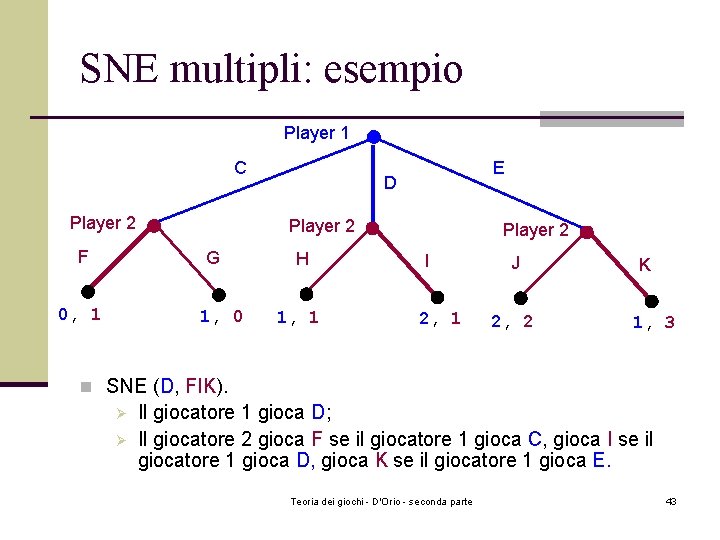
SNE multipli: esempio Player 1 C Player 2 F D Player 2 G 0, 1 E 1, 0 H 1, 1 Player 2 I 2, 1 J 2, 2 K 1, 3 n SNE (D, FIK). Ø Ø Il giocatore 1 gioca D; Il giocatore 2 gioca F se il giocatore 1 gioca C, gioca I se il giocatore 1 gioca D, gioca K se il giocatore 1 gioca E. Teoria dei giochi - D'Orio - seconda parte 43

Il modello di duopolio alla Stackelberg n Un prodotto omogeneo è prodotto solo da due imprese: firm 1 and firm 2. Le quantità sono indicate rispettivamente come q 1 e q 2. n La sequenza di questo gioco è come segue: Ø Ø Firm 1 sceglie una quantità q 1 0. Firm 2 osserva q 1 e quindi sceglie una quantità q 2 0. n Il prezzo di mercato è P(Q)=a –Q, dove a è una costante e Q=q 1+q 2. n Il costo dell’impresa i di produrre la quantità qi è Ci(qi)=cqi. n Le funzioni di Payoff sono : u 1(q 1, q 2)=q 1(a–(q 1+q 2)–c) u 2(q 1, q 2)=q 2(a–(q 1+q 2)–c) Teoria dei giochi - D'Orio - seconda parte 44

Il modello di duopolio alla Stackelberg n Trovare, per backward induction, il SNE Ø Prima risolviamo il problema dell’impresa 2 per ogni q 1 0 in modo da ottenre la funzione di risposta ottima dell’impresa 2 a q 1. Vale a dire, risolviamo tutti i sottogiochi che cominciano dalla mossa dell’impresa 2. Ø Fatto ciò, risolviamo il problema dell’impresa 1. Vale a dire, risolviamo il sottogioco che ha inizio dalla mossa dell’impresa 1 Teoria dei giochi - D'Orio - seconda parte 45

Il modello di duopolio alla Stackelberg n Risolvere il problema dell’impresa 2 per ogni q 1 0 in modo da ottenere la risposta ottima dell’impresa 2 a ogni q 1. Ø Max u 2(q 1, q 2)=q 2(a–(q 1+q 2)–c) s. a 0 q 2 +∞ FOC: a – 2 q 2 – q 1 – c = 0 Ø Ø La risposta ottima dell’impresa 2 sarà, R 2(q 1) = (a – q 1 – c)/2 se q 1 a– c = 0 se q 1 > a– c Teoria dei giochi - D'Orio - seconda parte 46

Il modello di duopolio alla Stackelberg n Risolvere il problema dell’impresa 1. Notate che l’impresa 1 può risolvere anche il problema dell’impresa 2 (common knowledge). Vale a dire, l’impresa 1 conosce la risposta ottima dell’impresa 2 a ogni quantità 1 q 1. Quindi, il problema dell’impresa 1 sarà: Ø Max u 1(q 1, R 2(q 1))=q 1(a–(q 1+R 2(q 1))–c) s. a 0 q 1 +∞ Vale a dire, Max u 1(q 1, R 2(q 1))=q 1(a–q 1–c)/2 s. a 0 q 1 +∞ FOC: (a – 2 q 1 – c)/2 = 0 q 1 = (a – c)/2 Teoria dei giochi - D'Orio - seconda parte 47

Il modello di duopolio alla Stackelberg n Equilibrio di Nash perfetto nei sottogiochi Ø ( (a – c)/2, R 2(q 1) ), dove R 2(q 1) = (a – q 1 – c)/2 se q 1 a– c = 0 if q 1 > a– c Ø Vale a dire, l’impresa 1 sceglie una quantità (a – c)/2, l’impresa 2 sceglie una quantità R 2(q 1) se l’impresa 1 sceglierà una quantità q 1. Ø Il risultato della backward induction è ( (a – c)/2, (a – c)/4 ). Ø L’impresa 1 sceglie una quantità (a – c)/2, l’impresa 2 sceglie una quantità (a – c)/4. Teoria dei giochi - D'Orio - seconda parte 48

Il modello di duopolio alla Stackelberg n L’impresa 1 produrrà q 1=(a – c)/2 e il suo profitto sarà q 1(a–(q 1+ q 2)–c)=(a–c)2/8 n L’impresa 3 produrrà q 2=(a – c)/4 e il suo profitto sarà q 2(a–(q 1+ q 2)–c)=(a–c)2/16 n La quantità totale prodotta dalle due imprese sarà 3(a – c)/4. Teoria dei giochi - D'Orio - seconda parte 49

Il modello di duopolio alla Cournot n L’impresa 1 produce q 1=(a – c)/3 e il suo profitto sarà q 1(a–(q 1+ q 2)–c)=(a–c)2/9 n L’impresa 2 produce q 2=(a – c)/3 e il suo profitto sarà q 2(a–(q 1+ q 2)–c)=(a–c)2/9 n La quantità totale prodotta dalle due imprese sarà 2(a – c)/3. Teoria dei giochi - D'Orio - seconda parte 50

Il monopolio n Supponiate che ci sia una sola impresa, un monopolio, che produce il prodotto. Il monopolista, per decidere la quantità qm, deve risolvere il seguente problema: n Max qm (a–qm–c) s. a 0 qm +∞ FOC: a – 2 qm – c = 0 qm = (a – c)/2 n Il monopolista produce qm=(a – c)/2 e il suo profitto sarà qm(a–qm–c)=(a–c)2/4 Teoria dei giochi - D'Orio - seconda parte 51

Il modello di duopolio alla Bertrand: mosse successive e prodotti differenziati n Due imprese: impresa 1 e impresa 2. n Ogni impresa sceglie il prezzo per il proprio prodotto. I prezzi sono rispettivamente indicati con p 1 e p 2. n La sequenza di questo gioco è come segue: Ø Ø L’impresa 1 sceglie un prezzo p 1 0. L’impresa 2 osserva p 1 e quindi sceglie p 2 0. n La quantità domandata dai consumatori all’impresa 1: q 1(p 1, p 2) = a – p 1 + bp 2. n La quantità domandata dai consumatori all’impresa 2: q 2(p 1, p 2) = a – p 2 + bp 1. n I costi dell’impresa i di produrre la quantità qi sono: Ci(qi)=cqi. Teoria dei giochi - D'Orio - seconda parte 52

Il modello di duopolio alla Bertrand: mosse successive e prodotti differenziati n Risolvere il problema dell’impresa 2 per ogni p 1 0 per ottenere la funzione di risposta ottima ad ogni p 1. Ø Max u 2(p 1, p 2)=(a – p 2 + bp 1 )(p 2 – c) s. a 0 p 2 +∞ FOC: a + c – 2 p 2 + bp 1 = 0 p 2 = (a + c + bp 1)/2 Ø La Ø risposta ottima dell’impresa 2 sarà, R 2(p 1) = (a + c + bp 1)/2 Teoria dei giochi - D'Orio - seconda parte 53

Il modello di duopolio alla Bertrand: mosse successive e prodotti differenziati n Risolvere il problema dell’impresa 1. Notate che l’impresa 1 può risolvere il problema dell’impresa 2 (common knowledge). L’impresa 1 conosce quindi la funzione di risposta ottima dell’impresa 2 a p 1. Quindi il problema dell’impresa 1 sarà: Ø Max u 1(p 1, R 2(p 1))=(a – p 1 + b R 2(p 1) )(p 1 – c) s. a 0 p 1 +∞ Vale a dire, Max u 1(p 1, R 2(p 1))=(a – p 1 + b (a + c + bp 1)/2 )(p 1 – c) s. a 0 p 1 +∞ Ø F. O. C. : a – p 1 + b (a + c + bp 1)/2+(– 1+b 2/2) (p 1 – c) = 0 p 1 = (a+c+(ab+bc–b 2 c)/2)/(2–b 2) Teoria dei giochi - D'Orio - seconda parte 54

Il modello di duopolio alla Bertrand: mosse successive e prodotti differenziati n Equilibrio di Nash perfetto nei sottogiochi 2 2 Ø ((a+c+(ab+bc–b c)/2)/(2–b ), R 2(p 1) ), dove R 2(p 1) = (a + c + bp 1)/2 Ø L’impresa 1 sceglie un prezzo (a+c+(ab+bc–b 2 c)/2)/(2–b 2), Ø L’impresa 2 sceglie un prezzo R 2(p 1) se l’impresa 1 sceglie un prezzo p 1. Teoria dei giochi - D'Orio - seconda parte 55

Riassunto n Equilibrio di Nash perfetto nei sottogiochi n Backward induction n Modello di duopolio alla Stackelberg n Modello di duopolio alla Bertrand a mosse successive e prodotti differenziati n Prossimo argomento n Giochi dinamici ad informazione completa ma imperfetta Teoria dei giochi - D'Orio - seconda parte 56

Giochi dinamici ad informazione completa ed imperfetta n Informazione imperfetta Ø Un giocatore potrebbe non conoscere CHI ha fatto COSA nel momento in cui si trova a dover compiere una scelta. Ø Esempio: Il giocatore 2 fa la sua scelta dopo il giocatore 1. Il giocatore 2 ha bisogno di prendere la propria decisione senza sapere cosa ha fatto il giocatore 1. Teoria dei giochi - D'Orio - seconda parte 57

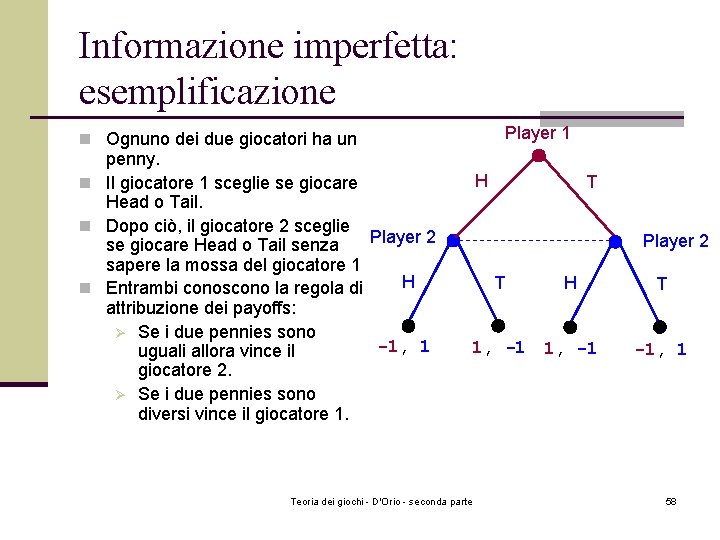
Informazione imperfetta: esemplificazione Player 1 n Ognuno dei due giocatori ha un penny. n Il giocatore 1 sceglie se giocare Head o Tail. n Dopo ciò, il giocatore 2 sceglie Player 2 se giocare Head o Tail senza sapere la mossa del giocatore 1 H n Entrambi conoscono la regola di attribuzione dei payoffs: Ø Se i due pennies sono -1, 1 uguali allora vince il giocatore 2. Ø Se i due pennies sono diversi vince il giocatore 1. H T Player 2 T H 1, -1 Teoria dei giochi - D'Orio - seconda parte T -1, 1 58

Insieme informativo n Definizione del Gibbons: Un insieme informativo per un giocatore è una serie di nodi che soddisfa: Ø Ø Il giocatore ha la mossa ad ogni nodo dell’insieme informativo, e Quando il gioco raggiunge un nodo in un insieme informativo, il giocatore che deve muovere non sa quale nodo dell’insieme informativo è stato raggiunto. n Tutti i nodi di un insieme informativo appartengono allo stesso giocatore n Il giocatore deve avere lo stesso insieme di azioni possibili ad ogni nodo dell’insieme informativo. Teoria dei giochi - D'Orio - seconda parte 59

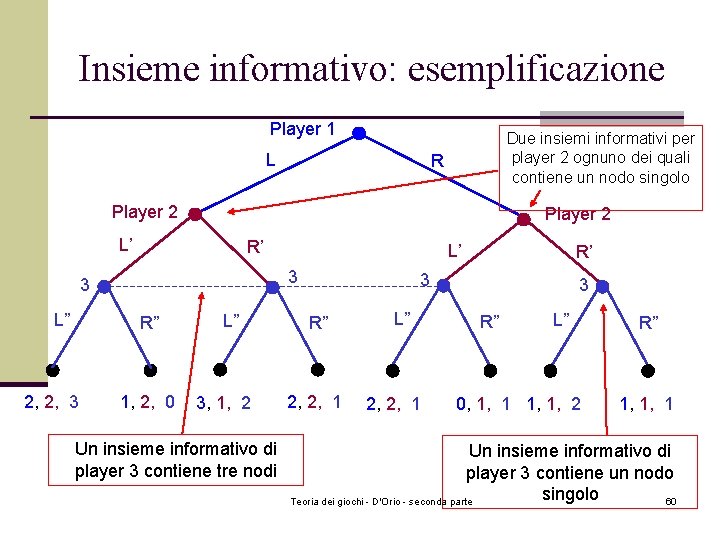
Insieme informativo: esemplificazione Player 1 L Due insiemi informativi per player 2 ognuno dei quali contiene un nodo singolo R Player 2 L’ R’ 3 3 L” R” 2, 2, 3 L’ 1, 2, 0 L” 3, 1, 2 Un insieme informativo di player 3 contiene tre nodi R’ 3 R” 2, 2, 1 L” 2, 2, 1 3 R” L” 0, 1, 1, 2 R” 1, 1, 1 Un insieme informativo di player 3 contiene un nodo singolo Teoria dei giochi - D'Orio - seconda parte 60

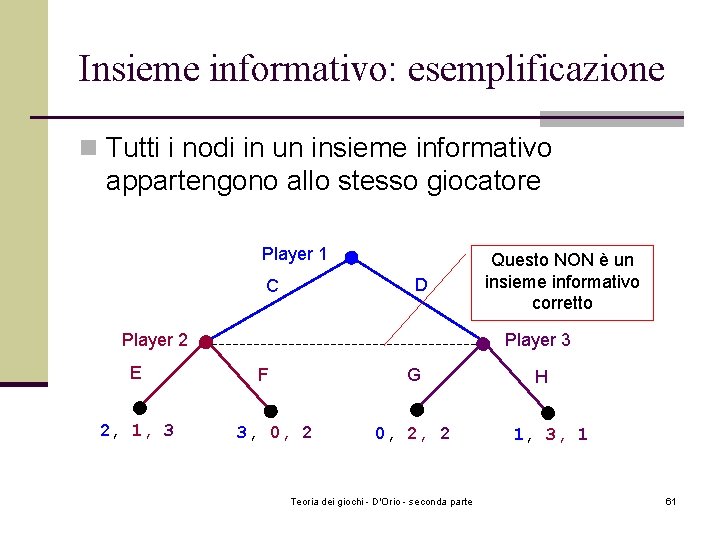
Insieme informativo: esemplificazione n Tutti i nodi in un insieme informativo appartengono allo stesso giocatore Player 1 D C Player 2 E 2, 1, 3 Questo NON è un insieme informativo corretto Player 3 F G 3, 0, 2, 2 Teoria dei giochi - D'Orio - seconda parte H 1, 3, 1 61

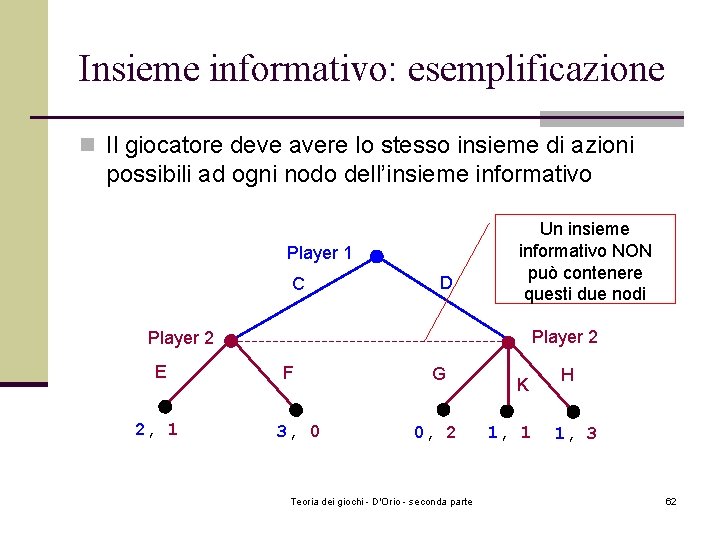
Insieme informativo: esemplificazione n Il giocatore deve avere lo stesso insieme di azioni possibili ad ogni nodo dell’insieme informativo Player 1 C D Un insieme informativo NON può contenere questi due nodi Player 2 E 2, 1 F 3, 0 G 0, 2 Teoria dei giochi - D'Orio - seconda parte K 1, 1 H 1, 3 62

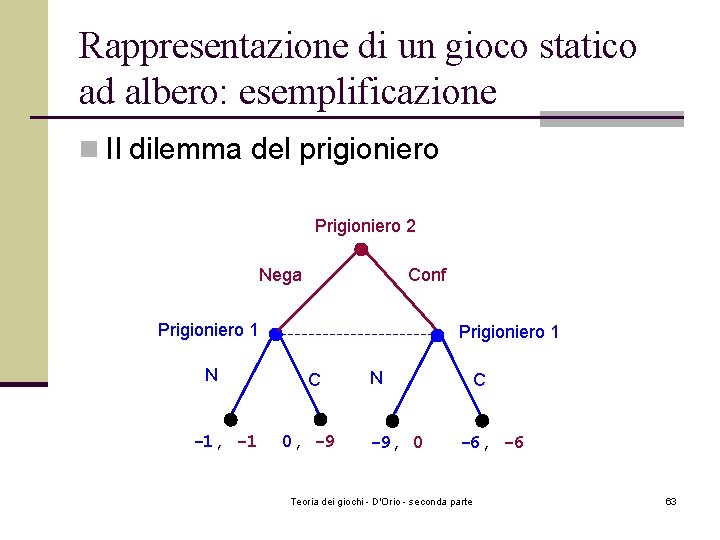
Rappresentazione di un gioco statico ad albero: esemplificazione n Il dilemma del prigioniero Prigioniero 2 Nega Conf Prigioniero 1 N -1, -1 Prigioniero 1 C 0, -9 N -9, 0 C -6, -6 Teoria dei giochi - D'Orio - seconda parte 63

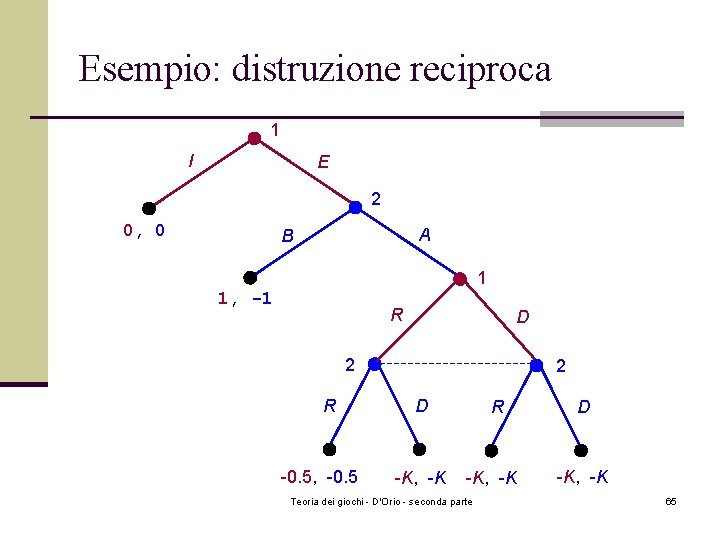
Esempio: distruzione mutualmente assicurata n Fra le due superpotenze, 1 e 2, c’è stato un incidente diplomatico. La sequenza è come segue: n Il gioco comincia con la scelta della superpotenza 1 che può ignorare l’incidente ( I ), ottenendo i payoffs (0, 0), o esasperare la situazione ( E ). n Se la superpotenza 1 esaspera, La superpotenza 2 può ritrattare ( B ), perdendo la faccia e ottenendo quindi un payoff negativo (1, -1), o può scegliere una risposta con attacco atomico ( A ). Su questa scelta, le due superpotenze giocano il seguente gioco a mosse simultanee. n Possono entrambe Ritrattare ( R ) o scegliere l’Attacco ( D ) nel qual caso il mondo è distrutto. Se entrambe scelgono di ritrattare entrambe hanno una piccola perdita e il payoff sarà (0. 5, -0. 5). Se entrambe scelgono l’attacco atomico il payoff sarà (-K, -K), dove K è un numero molto grande. Teoria dei giochi - D'Orio - seconda parte 64

Esempio: distruzione reciproca 1 I E 2 0, 0 A B 1 1, -1 R D 2 R -0. 5, -0. 5 2 D -K, -K R -K, -K Teoria dei giochi - D'Orio - seconda parte D -K, -K 65

Informazione perfetta e informazione imperfetta n Un gioco dinamico nel quale ogni insieme informativo contiene esattamente un nodo è chiamato gioco ad informazione perfetta. n Un gioco dinamico nel quale alcuni insiemi informativi contengono più di un nodo è chiamato gioco ad informazione imperfetta. Teoria dei giochi - D'Orio - seconda parte 66

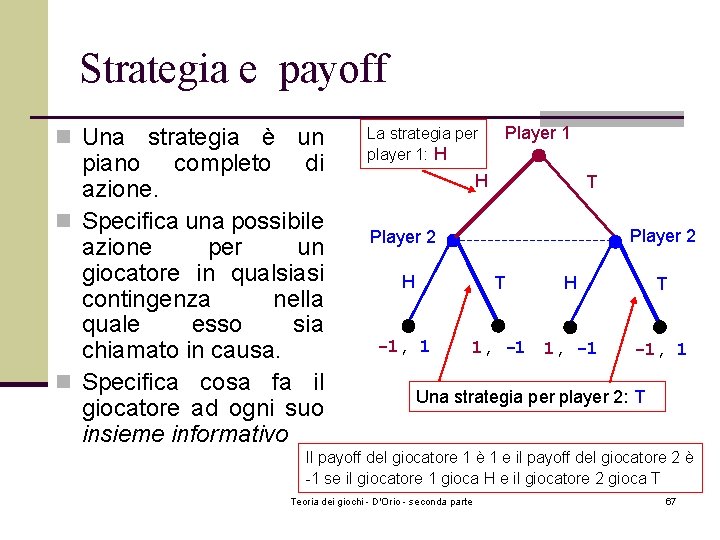
Strategia e payoff n Una strategia è un piano completo di azione. n Specifica una possibile azione per un giocatore in qualsiasi contingenza nella quale esso sia chiamato in causa. n Specifica cosa fa il giocatore ad ogni suo insieme informativo La strategia per player 1: H Player 1 H T Player 2 H T -1, 1 H 1, -1 T -1, 1 Una strategia per player 2: T Il payoff del giocatore 1 è 1 e il payoff del giocatore 2 è -1 se il giocatore 1 gioca H e il giocatore 2 gioca T Teoria dei giochi - D'Orio - seconda parte 67

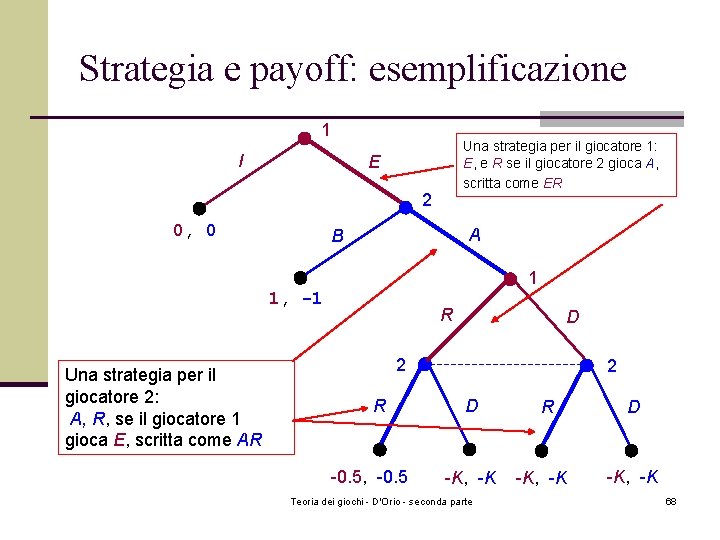
Strategia e payoff: esemplificazione 1 I Una strategia per il giocatore 1: E, e R se il giocatore 2 gioca A, scritta come ER E 2 0, 0 A B 1 1, -1 Una strategia per il giocatore 2: A, R, se il giocatore 1 gioca E, scritta come AR R D 2 R -0. 5, -0. 5 2 D -K, -K Teoria dei giochi - D'Orio - seconda parte R -K, -K D -K, -K 68

Il NE in un gioco dinamico n Possiamo usare anche la forma normale per rappresentare un gioco dinamico n L’insieme degli NE in un gioco dinamico ad informazione completa è l’insieme degli Nenella sua forma normale n Come trovare l’NE in un gioco dinamico ad informazione completa Costruite la forma normale del gioco dinamico ad informazione completa Ø Trovate l’NE nella forma normale Ø Teoria dei giochi - D'Orio - seconda parte 69

Rimuovere gli NE non ragionevoli n SNE è un NE raffinato n Puo eliminare NE non ragionevoli o minacce non credibili n Ma prima dobbiamo definire i sottogiochi Teoria dei giochi - D'Orio - seconda parte 70

Sottogioco n Un sottogioco in un albero di gioco dinamico Ø Ø Ø Comincia ad un insieme informativo singletone (che contiene un nodo singolo), e Include tutti i nodi e segmenti che seguono il singleton, e NON spezza nessun insieme informativo; vale a dire, se un nodo di un insieme informativo appartiene a questo sottogioco allora tutti i nodi dell’insieme informativo devono anche appartenere al sottogioco. Teoria dei giochi - D'Orio - seconda parte 71

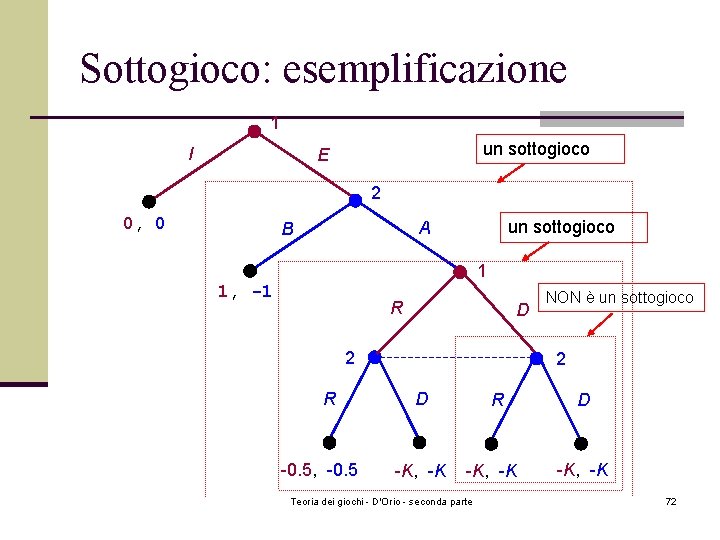
Sottogioco: esemplificazione 1 I un sottogioco E 2 0, 0 un sottogioco A B 1 1, -1 R D 2 R -0. 5, -0. 5 NON è un sottogioco 2 D -K, -K R -K, -K Teoria dei giochi - D'Orio - seconda parte D -K, -K 72

Equilibrio di Nash perfetto nei sottogiochi n L’NE di un gioco dinamico è perfetto nei sottogiochi se le strategie del NE costituiscono o inducono un NE in ogni sottogioco del gioco. n SNE è un NE. Teoria dei giochi - D'Orio - seconda parte 73

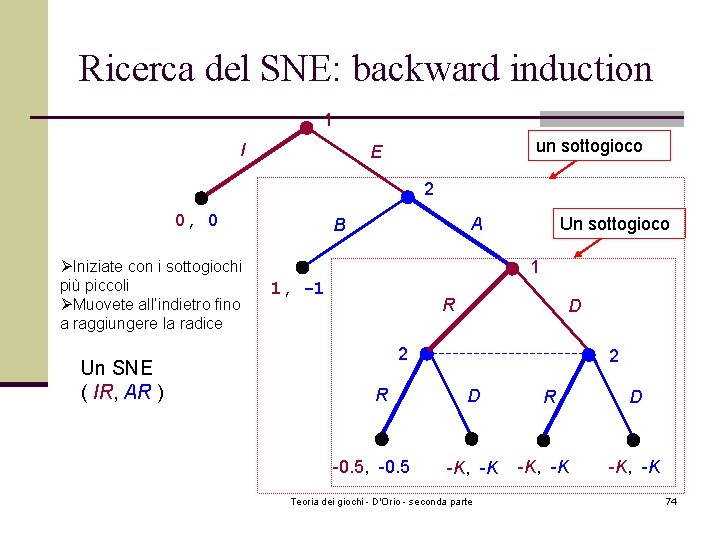
Ricerca del SNE: backward induction 1 I un sottogioco E 2 0, 0 ØIniziate con i sottogiochi più piccoli ØMuovete all’indietro fino a raggiungere la radice Un SNE ( IR, AR ) Un sottogioco A B 1 1, -1 R D 2 R -0. 5, -0. 5 2 D -K, -K Teoria dei giochi - D'Orio - seconda parte R -K, -K D -K, -K 74

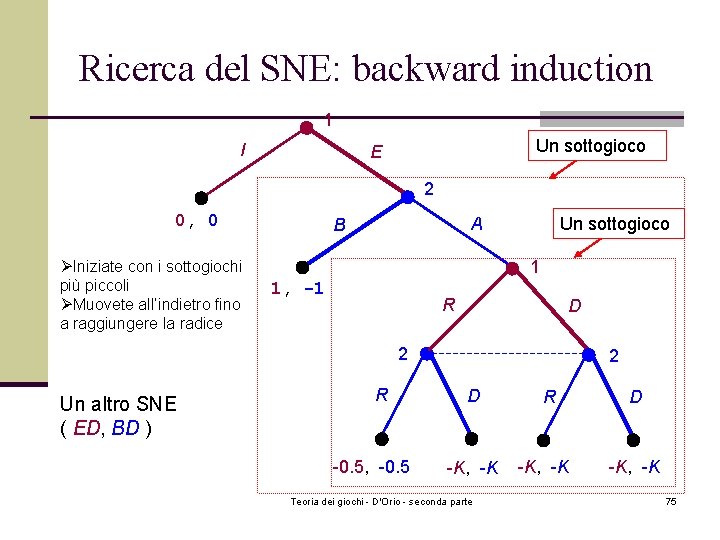
Ricerca del SNE: backward induction 1 I Un sottogioco E 2 0, 0 ØIniziate con i sottogiochi più piccoli ØMuovete all’indietro fino a raggiungere la radice Un sottogioco A B 1 1, -1 R D 2 Un altro SNE ( ED, BD ) R -0. 5, -0. 5 2 D -K, -K Teoria dei giochi - D'Orio - seconda parte R -K, -K D -K, -K 75

Investimento Bancario n Due investitori, 1 e 2, hanno ognuno un deposito di D con una banca. n La banca ha investito questi depositi in un progetto a lungo termine. Se la banca liquida gli investimenti prima che il progetto maturi, si ottiene un totale di 2 r, dove D > r > D/2. n Se l’investimento bancario invece matura, il progetto pagherà un capitale pari a 2 R, dove R>D. n Ci sono due date soltanto nelle quali gli investitori possono prelevare i soldi investiti nella banca. Teoria dei giochi - D'Orio - seconda parte 76

Investimenti bancari: sequenza del gioco n La sequenza del gioco è come segue n Data 1 (prima che l’investimento bancario maturi) Ø Ø I due investitori giocano un gioco a mosse simultanee Se entrambi prelevano alloro ognuno riceve r e il gioco finisce Se solo uno fa un prelievo allora lui riceve D, l’altro riceve 2 r-D, e il gioco finisce Se nessuno fa un prelevamento allora il progetto matura il rendimento e il gioco continua alla Data 2. n Data 2 (dopo che l’investimento ha maturato rendimenti) Ø Ø Due investitori giocano un gioco a mosse simultanee Se entrambi fanno prelevamenti allora ognuno riceve R e il gioco finisce Se solo uno preleva allora lui riceve 2 R-D, l’altro riceve D, e il gioco finisce Se nessuno preleva allora la banca restituisce R a ogni investitore e il gioco finisce. Teoria dei giochi - D'Orio - seconda parte 77

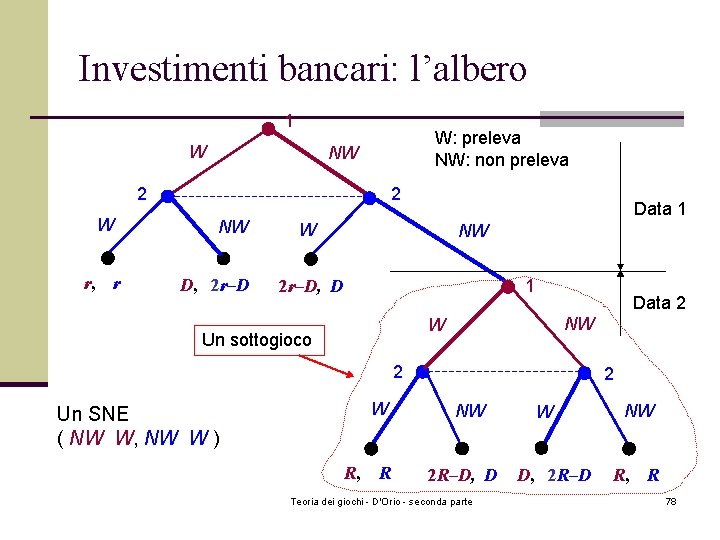
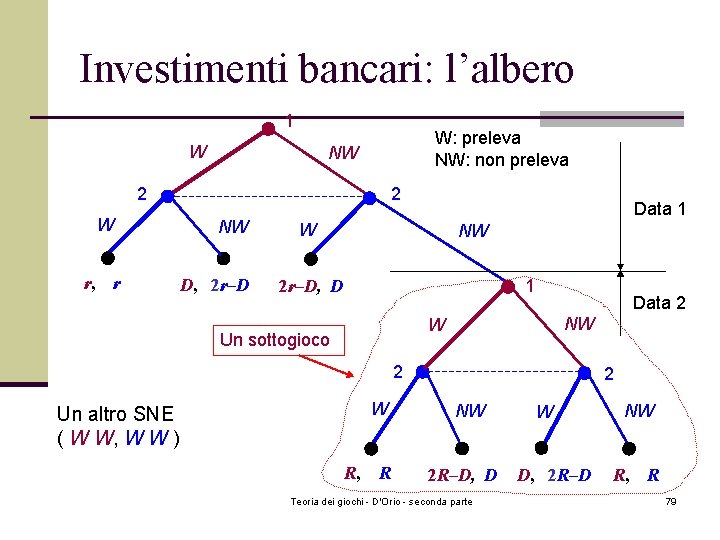
Investimenti bancari: l’albero 1 W W: preleva NW: non preleva NW 2 W r, r 2 NW D, 2 r–D Data 1 W NW 1 2 r–D, D Data 2 NW W Un sottogioco 2 Un SNE ( NW W, NW W ) W R, R 2 NW 2 R–D, D Teoria dei giochi - D'Orio - seconda parte W D, 2 R–D NW R, R 78

Investimenti bancari: l’albero 1 W W: preleva NW: non preleva NW 2 W r, r 2 NW D, 2 r–D Data 1 W NW 1 2 r–D, D Data 2 NW W Un sottogioco 2 Un altro SNE ( W W, W W ) W R, R 2 NW 2 R–D, D Teoria dei giochi - D'Orio - seconda parte W D, 2 R–D NW R, R 79

Dazi e concorrenza internazionale imperfetta n Due nazioni identiche, 1 e 2, scelgono simultaneamente i propri n n n dazi, denotati rispettivamente da t 1, t 2. L’impresa 1 della nazione 1 e l’impresa 2 dalla nazione 2 producono un prodotto omogeneo sia per il consumo interno sia per esportarlo. Dopo aver osservato i dazi scelti dalle due nazioni, l’impresa 1 e l’impresa w scelgono simultaneamente le quantità da destinare al consumo interno e all’esportazione, indicate rispettivamente con (h 1, e 1) e (h 2, e 2). I prezzi di mercato nelle due nazioni sono Pi(Qi)=a–Qi, for i=1, 2. Q 1=h 1+e 2, Q 2=h 2+e 1. Entrambe le imprese hanno costi marginali costanti c. Ogni impresa paga i dazi sulle esportazioni all’altra nazione. Teoria dei giochi - D'Orio - seconda parte 80

Dazi e concorrenza internazionale imperfetta Teoria dei giochi - D'Orio - seconda parte 81

Dazi e concorrenza internazionale imperfetta Teoria dei giochi - D'Orio - seconda parte 82

Backward induction: sottogioco tra le due imprese Teoria dei giochi - D'Orio - seconda parte 83

Backward induction: sottogioco tra le due imprese Teoria dei giochi - D'Orio - seconda parte 84

Backward induction: l’intero gioco Teoria dei giochi - D'Orio - seconda parte 85

Dazi e concorrenza internazionale imperfetta Teoria dei giochi - D'Orio - seconda parte 86

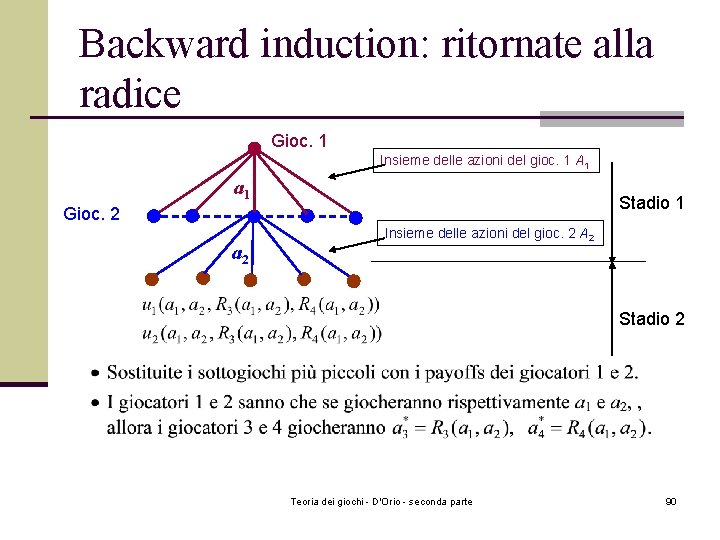
Generalizzazione del gioco dei dazi n Quattro giocatori: 1, 2, 3, 4. La sequenza del gioco è n n come segue: Stadio 1: I giocatori 1 e 2 scelgono simultaneamente le azioni a 1 e a 2 dall’insieme delle azioni rispettivamente possibili A 1 e A 2. Stadio 2: Dopo aver osservato il risultato (a 1, a 2) del primo stadio, I giocatori 3 e 4 scelgono simultaneamente le azioni a 3 e a 4 dall’insieme delle azioni rispettivamente possibili A 3 e A 4. Il gioco finisce. I payoff sono ui(a 1, a 2, a 3, a 4), per i=1, 2, 3, 4 Teoria dei giochi - D'Orio - seconda parte 87

Albero informale del gioco Gioc. 1 Insieme delle azioni del gioc. 1 A 1 a 1 Stadio 1 Gioc. 2 Gioc. 3 a 2 a 3 Insieme delle azioni del gioc. 2 A 2 Insieme delle azioni del gioc. 3 A 3 Stadio 2 Gioc. 4 a 4 Insieme delle azioni del gioc. 4 A 4 Uno dei sottogiochi più piccoli a seguito di (a 1, a 2) Teoria dei giochi - D'Orio - seconda parte 88

Backward induction: risolvete il sottogioco più piccolo Teoria dei giochi - D'Orio - seconda parte 89

Backward induction: ritornate alla radice Gioc. 1 Insieme delle azioni del gioc. 1 A 1 a 1 Stadio 1 Gioc. 2 a 2 Insieme delle azioni del gioc. 2 A 2 Stadio 2 Teoria dei giochi - D'Orio - seconda parte 90

Backward induction: ritornate alla radice Teoria dei giochi - D'Orio - seconda parte 91

Riassunto n Giochi dinamici ad informazione completa ed imperfetta n Equilibrio di Nash perfetto nei sottogiochi n Backward induction n Prossimo argomento n Giochi ripetuti Teoria dei giochi - D'Orio - seconda parte 92