Corso di Teoria dei Giochi Laurea specialistica in

Corso di Teoria dei Giochi Laurea specialistica in Economia Applicata Docente: Giovanni D’Orio E-mail: giovanni. dorio@unical. it Giochi statici (o a mosse simultanee) con informazione completa Teoria dei giochi - D'Orio - I parte 1

Prospetto di sintesi dei giochi statici ad informazione completa n Introduzione ai giochi n Rappresentazione in forma Normale (o strategica) n Eliminazione iterata delle strategie strettamente dominate n Equilibrio di Nash n Ripasso delle funzioni concave, ottimizzazione n Applicazione dell’equilibrio di Nash n Equilibrio di Nash in strategie miste Teoria dei giochi - D'Orio - I parte 2

Agenda n Che cosa è la teoria dei giochi n Esempi Ø Dilemma del prigioniero Ø La battaglia dei sessi Ø Matching pennies n Giochi statici ad informazione completa (o a mosse simultanee) n Rappresentazione in forma Normale o strategica Teoria dei giochi - D'Orio - I parte 3

Che cosa è la teoria dei giochi? n Noi ci concentreremo su giochi dove: Ø Ci sono almeno due giocatori razionali Ø Ogni giocatore ha più di una scelta Ø Il risultato finale dipende dalle strategie scelte da tutti i giocatori; c’è interazione strategica. n Esempio: Sei persone vanno ad un ristorante. Ø Ogni persona paga il proprio pasto – un problema semplice di decisione Ø Prima del pranzo, ogni persona è d'accordo a dividere il conto fra tutti i partecipanti – un gioco Teoria dei giochi - D'Orio - I parte 4

Che cosa è la teoria dei giochi? n La Teoria dei Giochi è un modo formale di analizzare l’interazione strategica tra un gruppo di giocatori (o agenti) razionali che si comportano strategicamente n La teoria dei giochi ha applicazioni Ø Economiche Ø Politiche Ø etc. Teoria dei giochi - D'Orio - I parte 5

Esempio Classico: Il Dilemma del prigioniero n Due sospetti detenuti in celle separate sono accusati di un crimine rilevante. Non ci sono però prove sufficienti. n Ad entrambi I sospetti viene comunicata la seguente regola: Ø Se nessuno confessa allora entrambi saranno accusati di un crimine minore e condannati ad un mese di carcere. Ø Se entrambi confessano allora entrambi saranno condannati a sei mesi di carcere. Ø Se uno confessa ma l’altro nega, allora chi confessa sarà rilasciato ma l’altro sconterà nove mesi di carcere. Prigioniero 2 Nega Prigioniero 1 Nega Confessa -1 , -1 0 , -9 Teoria dei giochi - D'Orio - I parte Confessa -9 , 0 -6 , -6 6

Esempio: La battaglia dei sessi n In posti separati, Chris e Pat devono scegliere di passare la serata all’opera o a un combattimento di boxe. n Sia Chris che Pat sanno quanto segue: Ø Ø Ø Entrambi vorrebbero passare la serata insieme. Ma Chris preferisce l’opera. Pat preferisce la boxe. Pat Opera Chris Boxe Opera 2 , 1 0 , 0 Boxe 0 , 0 1 , 2 Teoria dei giochi - D'Orio - I parte 7

Esempio: Matching pennies n Ognuno dei due giocatori ha una monetina. n I due giocatori devono scegliere simultaneamente se mostrare Testa o Croce. n Entrambi i giocatori conoscono le seguenti regole: Ø Se le due monetine hanno entrambi lo stesso esito (entrambe testa or entrambe croce) allora il giocatore 2 vince la moneta del giocatore 1. Ø In caso diverso, il giocatore 1 vince la moneta del giocatore 2. Giocatore 2 Testa Croce Giocatore 1 Testa Croce -1 , 1 1 , -1 Teoria dei giochi - D'Orio - I parte 1 , -1 -1 , 1 8

Gioco statico (o a mosse simultanee) con informazione completa Un gioco statico consiste di: n Un insieme di giocatori (almeno 2) n Per ogni giocatore, un insieme di strategie/azioni n Payoffs ottenuti da ogni giocatore data la combinazione delle strategie, o preferenze per ogni giocatore sulle combinazioni delle strategie Ø {Giocat. 1, Giocat. 2, . . . Giocat. n} Ø S 1 S 2. . . Sn Ø ui(s 1, s 2, . . . sn), per ogni s 1 S 1, s 2 S 2, . . . sn Sn. Teoria dei giochi - D'Orio - I parte 9

Gioco statico (o a mosse simultanee) con informazione completa n Mosse simultanee Ogni giocatore sceglie la propria strategia senza conoscere la scelta degli altri. n Informazione completa Ø Ogni strategia possibile di ogni giocatore e la funzione dei payoff sono conoscenza comune fra tutti I giocatori. n Assunzioni sui giocatori Ø Razionalità Ø • • Ø I giocatori vogliono massimizzare il proprio payoffs I giocatori sono dei calcolatori perfetti (no errori) Ogni giocatore sa che gli altri giocatori sono razionali Teoria dei giochi - D'Orio - I parte 10

Gioco statico (o a mosse simultanee) con informazione completa n I giocatori cooperano? No. Questi sono giochi non cooperativi n Il timing (la sequenza degli eventi) Ø Ogni giocatore i sceglie la propria strategia si senza conoscere la scelta altrui. Ø Solo adesso ogni giocatore i riceve il proprio payoff ui(s 1, s 2, . . . , sn). Ø Il gioco finisce Ø Teoria dei giochi - D'Orio - I parte 11

Definizione: Rappresentazione in forma normale o strategica n La rappresentazione in forma normale (o strategica) di un gioco G specifica: Ø Un insieme finito di giocatori {1, 2, . . . , n}, Ø Lo spazio delle strategie dei giocatori S 1 S 2. . . Sn e Ø Le funzioni di pay-off u 1 u 2. . . un dove ui : S 1 × S 2 ×. . . × Sn→R. Teoria dei giochi - D'Orio - I parte 12

Rappresentazione in forma normale: gioco a 2 giocatori n Rappresentazione Bi-matriciale n 2 giocatori: Player 1 e Player 2 n Ogni giocatore ha un numero finito di strategie n Esempio: S 1={s 11, s 12, s 13} S 2={s 21, s 22} Player 2 s 21 s 22 s 11 u 1(s 11, s 21), u 2(s 11, s 21) u 1(s 11, s 22), u 2(s 11, s 22) Player 1 s 12 u 1(s 12, s 21), u 2(s 12, s 21) u 1(s 12, s 22), u 2(s 12, s 22) s 13 u 1(s 13, s 21), u 2(s 13, s 21) u 1(s 13, s 22), u 2(s 13, s 22) Teoria dei giochi - D'Orio - I parte 13

Esempio Classico: Rappresentazione “normale” del Dilemma del Prig. n Insieme di giocatori: {Prigioniero 1, Prigioniero 2} n Insieme delle strategie: S 1 = S 2 = {Nega, Confessa} n Funzioni di Payoff : u 1(N, N)=-1, u 1(N, C)=-9, u 1(C, N)=0, u 1(C, C)=-6; u 2(N, N)=-1, u 2(N, C)=0, u 2(C, N)=-9, u 2(C, C)=-6 Prig. 2 Giocat. Nega Strateg. Prig. 1 Nega Confessa -1 , -1 0 , -9 Confessa -9 , 0 -6 , -6 Payoffs Teoria dei giochi - D'Orio - I parte 14

Esempio: La battaglia dei sessi Pat Opera Chris Boxe Opera 2 , 1 0 , 0 Boxe 0 , 0 1 , 2 n Rappresentazione in forma Normale: Ø Insieme giocatori: { Chris, Pat } (={Player 1, Player 2}) Ø Insieme strategie: S 1 = S 2 = { Opera, Boxe} Ø Funzioni di Payoff : u 1(O, O)=2, u 1(O, B)=0, u 1(B, O)=0, u 1(B, B)=1; u 2(O, O)=1, u 2(O, B)=0, u 2(B, O)=0, u 2(B, B)=2 Teoria dei giochi - D'Orio - I parte 15

Esempio: Matching pennies Player 2 Testa Croce Player 1 Testa Croce -1 , 1 1 , -1 -1 , 1 n Rappresentazione in forma normale: Ø Insieme giocatori: {Player 1, Player 2} Ø Insieme strategie: S 1 = S 2 = { Testa, Croce } Ø Funzioni di Payoff : u 1(T, T)=-1, u 1(T, C)=1, u 1(C, T)=1, u 1(C, C)=-1; u 2(T, T)=1, u 2(T, C)=-1, u 2(C, T)=-1, u 2(C, C)=1 Teoria dei giochi - D'Orio - I parte 16

Esempio: Turisti e Nativi n Solo due bars (bar 1, bar 2) in città n Si può applicare un prezzo di $2, $4, o $5 n 6000 turisti scelgono un bar casualmente n 4000 nativi scelgono il bar con il prezzo minore n Esempio 1: Entrambi fissano $2 Ø Ognuno guadagna 5, 000 clienti e $10, 000 n Esempio 2: Il Bar 1 fissa $4, Il Bar 2 fissa $5 Ø Bar 1 prende 3000+4000=7, 000 clienti e $28, 000 Ø Bar 2 prende 3000 clienti e $15, 000 Teoria dei giochi - D'Orio - I parte 17

Esempio: Il modello di duopolio di Cournot n Un prodotto è prodotto solo da 2 imprese: impresa 1 e impresa 2. Le quantità sono rispettivamente q 1 e q 2, . Ogni impresa sceglie la quantità senza conoscere la quantità scelta dall’altra. . n Il prezzo di mercato è P(Q)=a-Q, dove Q=q 1+q 2. n Il costo dell’impresa i di produrre qi è Ci(qi)=cqi. Rappresentazione in forma normale: Ø Ø Ø Insieme giocatori: { Firm 1, Firm 2} Insieme strategie: S 1=[0, +∞), S 2=[0, +∞) Funzione di Payoff : u 1(q 1, q 2)=q 1(a-(q 1+q 2)-c), u 2(q 1, q 2)=q 2(a-(q 1+q 2)-c) Teoria dei giochi - D'Orio - I parte 18

Ancora un esempio n Ognuno di n giocatori seleziona un numero tra 0 e 100 simultaneamente. Sia xi il numero selezionato dal giocatore i. n Sia y la media di questi numeri n Il payoff del giocatore i sia = xi – 3 y/5 La rappresentazione in forma normale: Teoria dei giochi - D'Orio - I parte 19

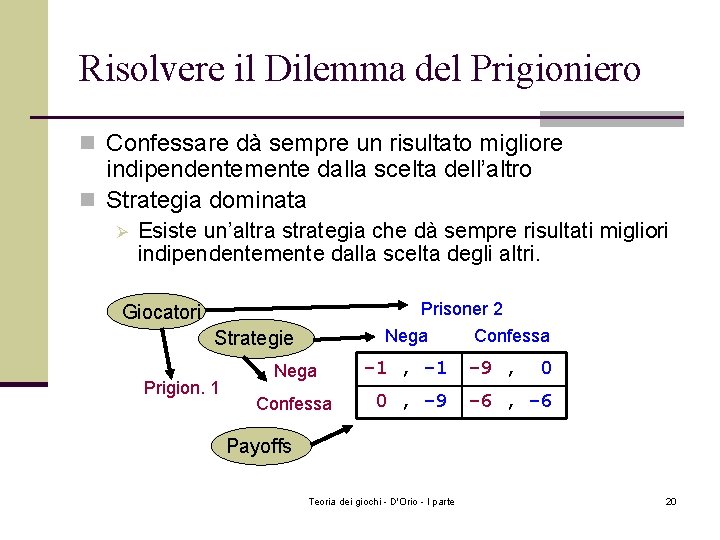
Risolvere il Dilemma del Prigioniero n Confessare dà sempre un risultato migliore indipendentemente dalla scelta dell’altro n Strategia dominata Ø Esiste un’altra strategia che dà sempre risultati migliori indipendentemente dalla scelta degli altri. Prisoner 2 Nega Confessa Giocatori Strategie Prigion. 1 Nega Confessa -1 , -1 0 , -9 -9 , 0 -6 , -6 Payoffs Teoria dei giochi - D'Orio - I parte 20

Definizione: strategie strettamente dominate si” è strettamente meglio di si’ Prig. 2 Indipend. Scelta altrui Nega Prig. 1 Confessa Nega -1 , -1 0 , -9 Teoria dei giochi - D'Orio - I parte Confessa -9 , 0 -6 , -6 21

Riassunto n Giochi statici ad informazione completa n Rappresentazione normale o strategica n Prossimo argomento n Strategie dominate n Eliminazione iterata di strategie strettamente dominate n Equilibrio di Nash Teoria dei giochi - D'Orio - I parte 22

Ripasso veloce n La forma normale di un gioco G specifica: Ø Ø Ø Un insieme finito di giocatori {1, 2, . . . , n}, Lo spazio delle strategie dei giocatori S 1 S 2. . . Sn e Le loro funzioni di payoff u 1 u 2. . . un dove ui : S 1 × S 2 ×. . . × Sn→R. Tutte le combinazioni delle strategie. Una combinazione di strategie è un insieme di strategie, una per ogni giocatore Prig. 2 Nega Prig. 1 Confessa Nega -1 , -1 -9 , 0 Confessa 0 , -9 -6 , -6 Teoria dei giochi - D'Orio - I parte 23

Definizione: strategie strettamente dominate si” è strettamente meglio di si’ Prig. 2 Indipend. Scelta altrui Nega Prig. 1 Confessa Nega -1 , -1 0 , -9 Teoria dei giochi - D'Orio - I parte Confessa -9 , 0 -6 , -6 24

Esempio n Due imprese, Reynolds e Philip, si dividono il mkt. n Ogni impresa guadagna $60 milioni dalla propria clientela se nessuna fa pubblicità (Ad) n La pubblicità costa all’impresa $20 milioni n La pubblicità attrae $30 milioni di fatturato dell’altro concorrente Philip No Ad Reynolds Ad No Ad 60 , 60 30 , 70 Ad 70 , 30 40 , 40 Teoria dei giochi - D'Orio - I parte 25

Gioco a 2 con strategie finite n S 1={s 11, s 12, s 13} S 2={s 21, s 22} n s 11 è strettamente dominata da s 12 se u 1(s 11, s 21)<u 1(s 12, s 21) e u 1(s 11, s 22)<u 1(s 12, s 22). n s 21 è strettamente dominata da s 22 se u 2(s 1 i, s 21) < u 2(s 1 i, s 22), per i = 1, 2, 3 Player 2 s 21 s 22 s 11 u 1(s 11, s 21), u 2(s 11, s 21) u 1(s 11, s 22), u 2(s 11, s 22) Player 1 s 12 u 1(s 12, s 21), u 2(s 12, s 21) u 1(s 12, s 22), u 2(s 12, s 22) s 13 u 1(s 13, s 21), u 2(s 13, s 21) u 1(s 13, s 22), u 2(s 13, s 22) Teoria dei giochi - D'Orio - I parte 26

Definizione: strategie debolmente dominate si” è almeno tanto buono quanto si’ Player 2 Qualsiasi sia la scelta altrui Player 1 L R U 1 , 1 2 , 0 B 0 , 2 2 , 2 Teoria dei giochi - D'Orio - I parte 27

Strategie dominate in modo stretto o in modo debole n Un giocatore razionale non sceglie mai strategie strettamente dominate. Quindi ogni strategia strettamente dominata può essere eliminata. n Un giocatore razionale può scegliere una strategia debolmente dominata. Teoria dei giochi - D'Orio - I parte 28

Eliminazione iterata di strategie strettamente dominate n Se una strategia è strettamente dominata, eliminatela n La dimensione e complessità del gioco risulterà ridotta n Eliminate ogni strategia strettamente dominata dal gioco ridotto n Continuate le eliminazioni finchè non ci saranno più strategie strettam. dominate Teoria dei giochi - D'Orio - I parte 29

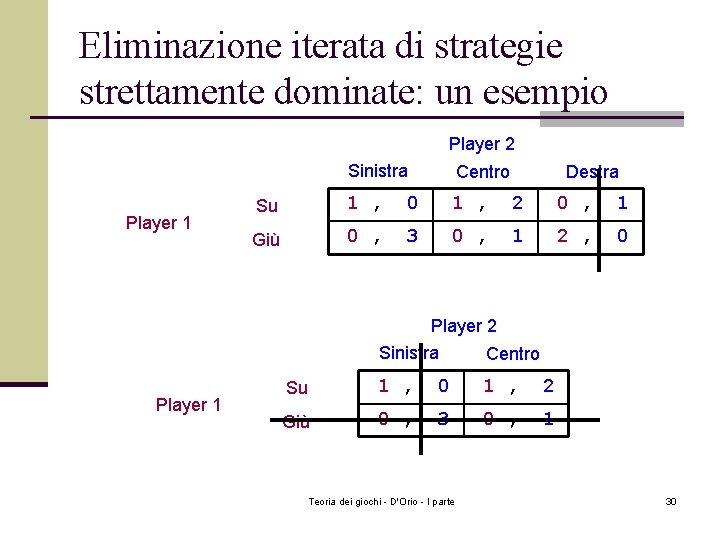
Eliminazione iterata di strategie strettamente dominate: un esempio Player 2 Player 1 Sinistra Centro Su 1 , 0 1 , 2 0 , 1 Giù 0 , 3 0 , 1 2 , 0 Destra Player 2 Sinistra Centro Player 1 Su 1 , 0 1 , 2 Giù 0 , 3 0 , 1 Teoria dei giochi - D'Orio - I parte 30

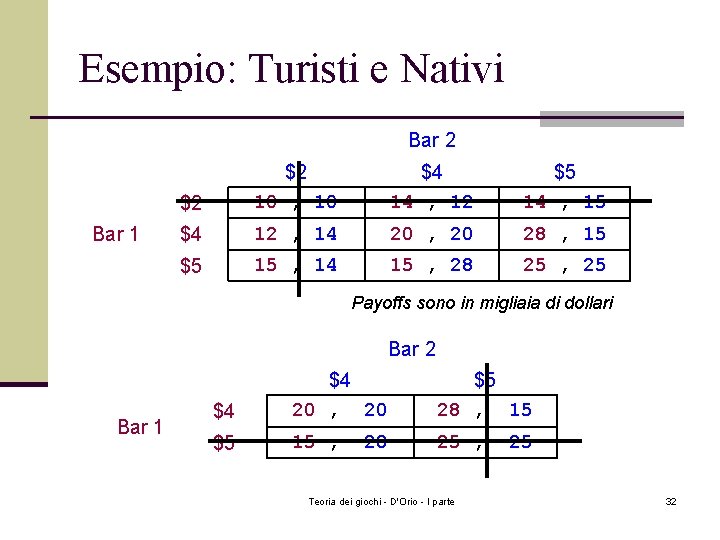
Esempio: Turisti e Nativi n Solo due bar (bar 1, bar 2) in una città n Si possono fissare prezzi di $2, $4, o $5 n 6000 turisti scelgono un bar casualmente n 4000 nativi selezionano il bar con il prezzo inferiore n Esempio 1: Entrambi fissano $2 Ø Ognuno attrae 5, 000 clienti e $10, 000 n Esempio 2: Bar 1 fissa $4, Bar 2 fissa $5 Ø Bar 1 attrae 3000+4000=7, 000 clienti e $28, 000 Ø Bar 2 attrae 3000 clienti e $15, 000 Teoria dei giochi - D'Orio - I parte 31

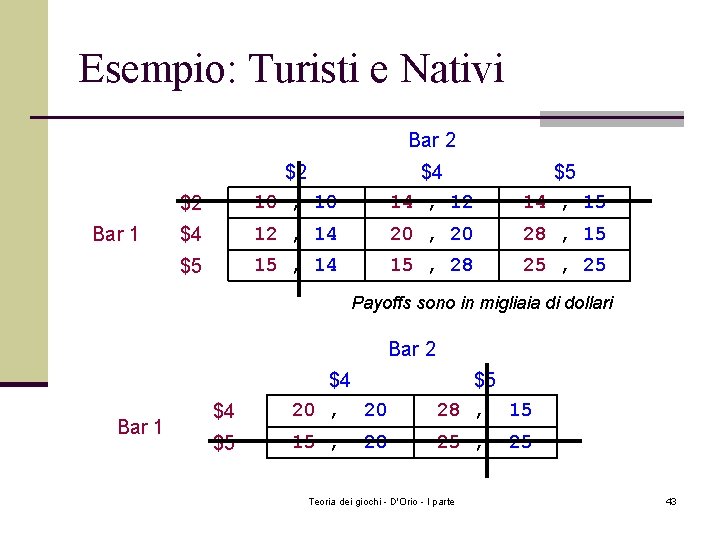
Esempio: Turisti e Nativi Bar 2 Bar 1 $2 $2 10 , 10 $4 14 , 12 $5 14 , 15 $4 12 , 14 20 , 20 28 , 15 $5 15 , 14 15 , 28 25 , 25 Payoffs sono in migliaia di dollari Bar 2 Bar 1 $4 $4 20 , 20 $5 28 , 15 $5 15 , 28 Teoria dei giochi - D'Orio - I parte 25 32

Ancora un esempio n Ognuno di n giocatori seleziona un numero tra 0 e 100 simultaneamente. Sia xi il numero selezionato dal giocatore i. n Sia y la media di questi numeri n Il payoff del giocatore I sarà = xi – 3 y/5 Teoria dei giochi - D'Orio - I parte 33

Un esempio ulteriore n La rappresentazione in forma normale: Ø Giocatori: {player 1, player 2, . . . , player n} Ø Strategie: Si =[0, 100], per i = 1, 2, . . . , n. Ø Funzione di payoff: ui(x 1, x 2, . . . , xn) = xi – 3 y/5 n Ci sono strategie dominate? n Quali numeri dovrebbero essere selezionati? Teoria dei giochi - D'Orio - I parte 34

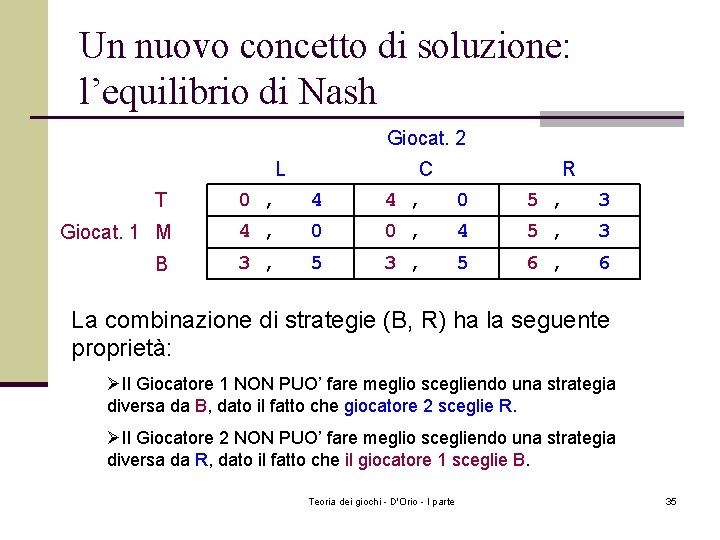
Un nuovo concetto di soluzione: l’equilibrio di Nash Giocat. 2 L T 0 , 4 C 4 , 0 R 5 , 3 Giocat. 1 M 4 , 0 0 , 4 5 , 3 B 3 , 5 6 , 6 La combinazione di strategie (B, R) ha la seguente proprietà: ØIl Giocatore 1 NON PUO’ fare meglio scegliendo una strategia diversa da B, dato il fatto che giocatore 2 sceglie R. ØIl Giocatore 2 NON PUO’ fare meglio scegliendo una strategia diversa da R, dato il fatto che il giocatore 1 sceglie B. Teoria dei giochi - D'Orio - I parte 35

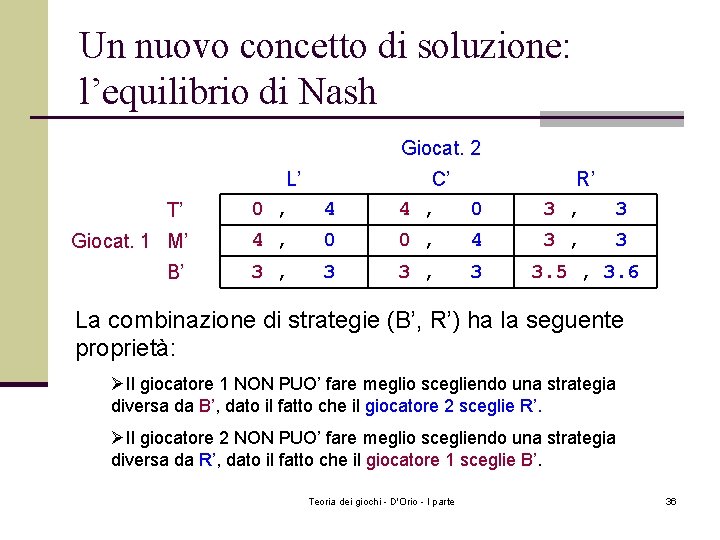
Un nuovo concetto di soluzione: l’equilibrio di Nash Giocat. 2 L’ 0 , Giocat. 1 M’ B’ T’ 4 C’ 4 , 0 R’ 3 , 3 4 , 0 0 , 4 3 , 3 3. 5 , 3. 6 La combinazione di strategie (B’, R’) ha la seguente proprietà: ØIl giocatore 1 NON PUO’ fare meglio scegliendo una strategia diversa da B’, dato il fatto che il giocatore 2 sceglie R’. ØIl giocatore 2 NON PUO’ fare meglio scegliendo una strategia diversa da R’, dato il fatto che il giocatore 1 sceglie B’. Teoria dei giochi - D'Orio - I parte 36

Equilibrio di Nash : l’idea n L’equilibrio di Nash Ø Un insieme di strategie, una per ogni giocatore, tale che la strategia di ogni giocatore sia la migliore risposta possibile nel momento in cui gli altri giocatori stanno giocando le loro strategie di equilibrio. Ø BR to BR= Best response to a best response Teoria dei giochi - D'Orio - I parte 37

Definizione: L’equilibrio di Nash Data la scelta altrui, il giocat. i non può migliorare se devia da si* Prig. 2 Nega Prig. 1 Nega Confessa -1 , -1 -9 , 0 0 , -9 -6 , -6 Teoria dei giochi - D'Orio - I parte 38

Gioco a 2 giocatori con strategie finite n S 1={s 11, s 12, s 13} S 2={s 21, s 22} n (s 11, s 21)è un equilibrio di Nash se u 1(s 11, s 21) u 1(s 12, s 21), u 1(s 11, s 21) u 1(s 13, s 21) e u 2(s 11, s 21) u 2(s 11, s 22). Giocatore 2 Gioc. 1 s 22 s 11 u 1(s 11, s 21), u 2(s 11, s 21) u 1(s 11, s 22), u 2(s 11, s 22) s 12 u 1(s 12, s 21), u 2(s 12, s 21) u 1(s 12, s 22), u 2(s 12, s 22) s 13 u 1(s 13, s 21), u 2(s 13, s 21) u 1(s 13, s 22), u 2(s 13, s 22) Teoria dei giochi - D'Orio - I parte 39

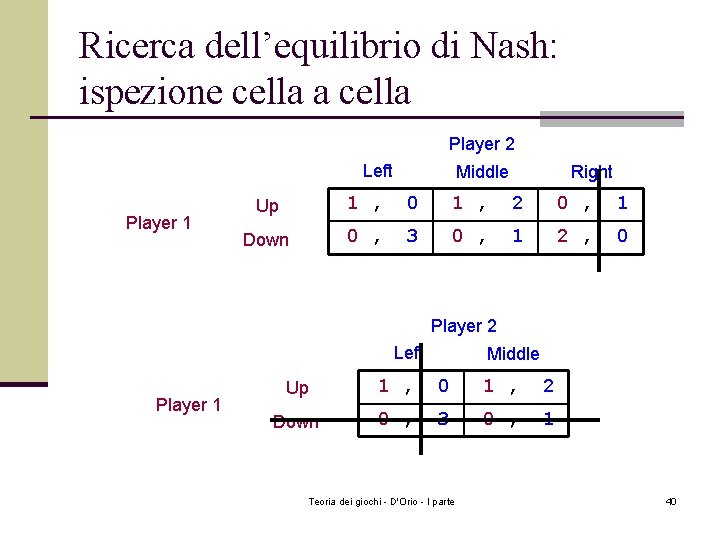
Ricerca dell’equilibrio di Nash: ispezione cella a cella Player 2 Left Player 1 Middle Right Up 1 , 0 1 , 2 0 , 1 Down 0 , 3 0 , 1 2 , 0 Player 2 Left Player 1 Middle Up 1 , 0 1 , 2 Down 0 , 3 0 , 1 Teoria dei giochi - D'Orio - I parte 40

Riassunto n Strategie dominate n Eliminazione iterata n Equilibrio di Nash n Prossimo argomento n Equilibrio di Nash n Funzione di risposta ottima Teoria dei giochi - D'Orio - I parte 41

Equilibrio di Nash : idea n Equilibrio di Nash Ø Un insieme di strategie, una per ogni giocatore, tale che la strategia di ogni giocatore sia la sua migliore possibile considerato che tutti gli altri giocatori stanno giocando la loro migliore strategia o Ø Una situazione stabile nella quale nessun giocatore vuole deviare se gli altri confermano la propria posizione Prig. 2 (Confessa, Confessa) è un equilibro di Nash. Prig. 1 Nega Confessa Nega -1 , -1 -9 , 0 Confessa 0 , -9 -6 , -6 Teoria dei giochi - D'Orio - I parte 42

Esempio: Turisti e Nativi Bar 2 Bar 1 $2 $2 10 , 10 $4 14 , 12 $5 14 , 15 $4 12 , 14 20 , 20 28 , 15 $5 15 , 14 15 , 28 25 , 25 Payoffs sono in migliaia di dollari Bar 2 Bar 1 $4 $4 20 , 20 $5 28 , 15 $5 15 , 28 Teoria dei giochi - D'Orio - I parte 25 43

Ancora quell’esempio n Rappresentazione in forma normale: Ø Giocatori: {player 1, player 2, . . . , player n} Ø Strategie: Si =[0, 100], for i = 1, 2, . . . , n. Ø Funzioni di Payoff : ui(x 1, x 2, . . . , xn) = xi – 3 y/5 n Quale è l’equilibrio di Nash? Teoria dei giochi - D'Orio - I parte 44

Funzione di risposta ottima: esempio Player 2 Player 1 n n T’ L’ 0 , 4 C’ 4 , M’ B’ 0 R’ 3 , 3 4 , 0 0 , 4 3 , 3 3. 5 , 3. 6 Se Player 2 sceglie L’ allora la strategia ottima di Player 1 è M’ Se Player 2 sceglie C’ allora la strategia ottima di Player 1 è T’ Se Player 2 sceglie R’ allora la strategia ottima di Player 1 è B’ Se Player 1 sceglie B’ allora la strategia ottima di Player 2’ è R’ n Risposta ottima: la migliore strategia giocabile da un giocatore, data la strategia scelta da altri giocatori Teoria dei giochi - D'Orio - I parte 45

Esempio: Turisti e Nativi Bar 2 Bar 1 $2 $2 10 , 10 $4 14 , 12 $5 14 , 15 $4 12 , 14 20 , 20 28 , 15 $5 15 , 14 15 , 28 25 , 25 Payoffs in migliaia di dollari n Quale è la risposta ottima del Bar 1 alle strategie di Bar 2 pari a $2, $4 o $5? n Quale è la risposta ottima del Bar 2 alle strategie di Bar 1 pari a $2, $4 or $5? Teoria dei giochi - D'Orio - I parte 46

Gioco a 2 giocatori con strategie finite n S 1={s 11, s 12, s 13} S 2={s 21, s 22} n La strategia di Player 1 s 11 è la migliore risposta alla strategia di Player 2 s 21 se u 1(s 11, s 21) u 1(s 12, s 21) e u 1(s 11, s 21) u 1(s 13, s 21). Player 2 s 21 s 22 s 11 u 1(s 11, s 21), u 2(s 11, s 21) u 1(s 11, s 22), u 2(s 11, s 22) Player 1 s 12 u 1(s 12, s 21), u 2(s 12, s 21) u 1(s 12, s 22), u 2(s 12, s 22) s 13 u 1(s 13, s 21), u 2(s 13, s 21) u 1(s 13, s 22), u 2(s 13, s 22) Teoria dei giochi - D'Orio - I parte 47

Utilizzo delle funzioni di risposta ottima per trovare l’equilibrio di Nash n In un gioco a due giocatori, ( s 1, s 2 ) è un equilibrio di Nash se e solo se la strategia di player 1’ s 1 è la migliore risposta alla strategia di player 2 s 2, e la strategia di player 2 s 2 è la migliore risposta alla strategia di player 1 s 1. Prisoner 2 Mum Confess Prisoner 1 Mum Confess -1 , -1 0 , -9 Teoria dei giochi - D'Orio - I parte -9 , 0 -6 , -6 48

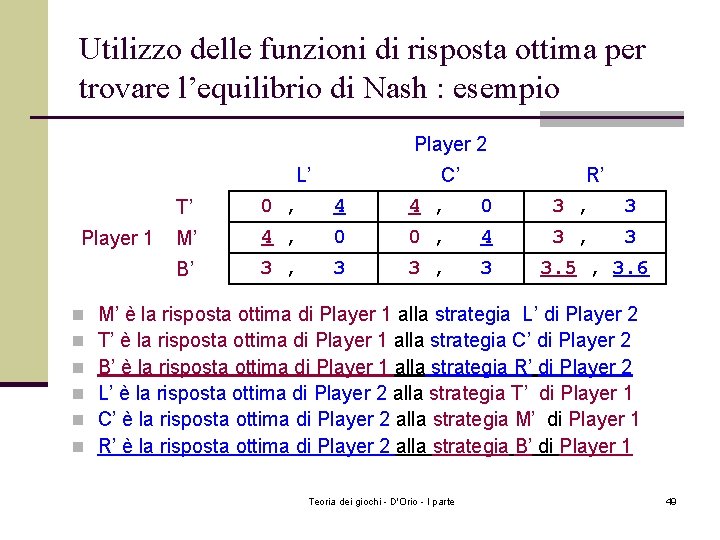
Utilizzo delle funzioni di risposta ottima per trovare l’equilibrio di Nash : esempio Player 2 Player 1 n n n T’ L’ 0 , 4 C’ 4 , M’ B’ 0 R’ 3 , 3 4 , 0 0 , 4 3 , 3 3. 5 , 3. 6 M’ è la risposta ottima di Player 1 alla strategia L’ di Player 2 T’ è la risposta ottima di Player 1 alla strategia C’ di Player 2 B’ è la risposta ottima di Player 1 alla strategia R’ di Player 2 L’ è la risposta ottima di Player 2 alla strategia T’ di Player 1 C’ è la risposta ottima di Player 2 alla strategia M’ di Player 1 R’ è la risposta ottima di Player 2 alla strategia B’ di Player 1 Teoria dei giochi - D'Orio - I parte 49

Esempio: Turisti e Nativi Bar 2 Bar 1 $2 $2 10 , 10 $4 14 , 12 $5 14 , 15 $4 12 , 14 20 , 20 28 , 15 $5 15 , 14 15 , 28 25 , 25 I Payoffs sono in migliaia di dollari Usate la funzione di rsposta ottima per trovare l’equilibrio di Nash. Teoria dei giochi - D'Orio - I parte 50

Esempio: La battaglia dei sessi Pat Opera Chris Prize Fight Opera 2 , 1 0 , 0 Prize Fight 0 , 0 1 , 2 n Opera è la risposta ottima di Player 1 alla strategia di Player 2 Opera n Opera è la risposta ottima di Player 2 alla strategia di Player 1 Opera Ø Quindi, (Opera, Opera) è un Equilibrio di Nash n Fight è la risposta ottima di Player 1 alla strategia di Player 2 Fight n Fight è la risposta ottima di Player 2 alla strategia di Player 1 Fight Ø Quindi, (Fight, Fight) è un Equilibrio di Nash Teoria dei giochi - D'Orio - I parte 51

Esempio: Matching pennies Player 2 Head Player 1 Head Tail -1 , Tail 1 1 , -1 -1 , 1 n Head è la risposta ottima di Player 1 alla strategia di Player 2 Tail n Tail è la risposta ottima di Player 2 alla strategia di Player 1 Tail n Tail è la risposta ottima di Player alla strategia di Player 2 Head n Head è la risposta ottima di Player 2 alla strategia di Player 1 Head Ø Quindi, NON c’è equilibrio di Nash Teoria dei giochi - D'Orio - I parte 52

Definizione: funzione di risposta ottima Date le strategie degli altri La risposta ottima di Player i Teoria dei giochi - D'Orio - I parte 53

Definizione: funzione di risposta ottima La risposta ottima di Player 1 alle strategie altrui è una soluzione d’ottimo di Teoria dei giochi - D'Orio - I parte 54

Utilizzo delle funzioni di risposta ottima per la definizione degli equilibri di Nash § Insieme di strategie, una per giocatore, tale che la strategia di ogni giocatore è per lui la migliore, assunto che gli altri stanno giocando le loro strategie ottime, o § Una situazione stabile che nessun giocatore vuole cambiare se gli altri non cambiano Teoria dei giochi - D'Orio - I parte 55

Riassunto n Equilibrio di Nash n Funzione di risposta ottima n Utilizzo della funzione di risposta ottima per la definizione dell’equilibrio di Nash n Utilizzo della funzione di risposta ottima per la determinazione dell’equilibrio di Nash n Prossimo argomento n Funzioni concave e ottimizzazione n Applicazioni Teoria dei giochi - D'Orio - I parte 56

Riassunto n In un gioco a n-giocatori in forma normale, se l’eliminazione iterata di strategie strettamente dominate elimina tutte le strategie tranne ( s 1*, s 2*, . . . , sn*), allora (s 1*, s 2*, . . . , sn*) è l’unico equilibrio di Nash. n In un gioco a n-giocatori in forma normale, se le strategie ( s 1*, s 2*, . . . , sn*) è un equilibrio di Nash allora esse sopravvivono all’eliminazione iterata di strategie strettamente dominate. Male strategie che superano l’eliminazione iterata di strategie strettamente dominate non necessariamente sono equilibri di Nash. Teoria dei giochi - D'Orio - I parte 57

Il modello del duopolio di Cournot n Un prodotto è realizzato solo da due imprese: impresa 1 e impresa 2. Le quantità sono denotate rispettivamente da q 1 e q 2, . Ogni impresa sceglie la propria quantità senza conoscere la scelta dell’altra. n Il prezzo di mercato è P(Q)=a-Q, dove a è una costante e Q=q 1+q 2. n Il costo dell’impresa i per produrre la quantità qi è Ci(qi)=cqi. Teoria dei giochi - D'Orio - I parte 58

Il modello del duopolio di Cournot La rappresentazione in forma normale: Insieme dei giocatori: { Impresa 1, Impresa 2} Ø Insieme delle strategie: S 1=[0, +∞), S 2=[0, +∞) Ø Funzioni di payoff: u 1(q 1, q 2)=q 1(a-(q 1+q 2)-c) u 2(q 1, q 2)=q 2(a-(q 1+q 2)-c) Ø Teoria dei giochi - D'Orio - I parte 59

Il modello del duopolio di Cournot n Come trovare l’equilibrio di Nash: Ø Trovate la coppia di quantità (q 1*, q 2*) tale che q 1* sia la risposta ottima dell’impresa 1 alla quantità q 2* dell’impresa 2 e q 2* sia la risposta ottima dell’impresa 2 alla quantità q 1* dell’impresa 1 Ø Ciò significa che, q 1* risolve Max u 1(q 1, q 2*)=q 1(a-(q 1+q 2*)-c) soggetto a 0 q 1 +∞ e q 2* risolve Max u 2(q 1*, q 2)=q 2(a-(q 1*+q 2)-c) soggetto a 0 q 2 +∞ Teoria dei giochi - D'Orio - I parte 60

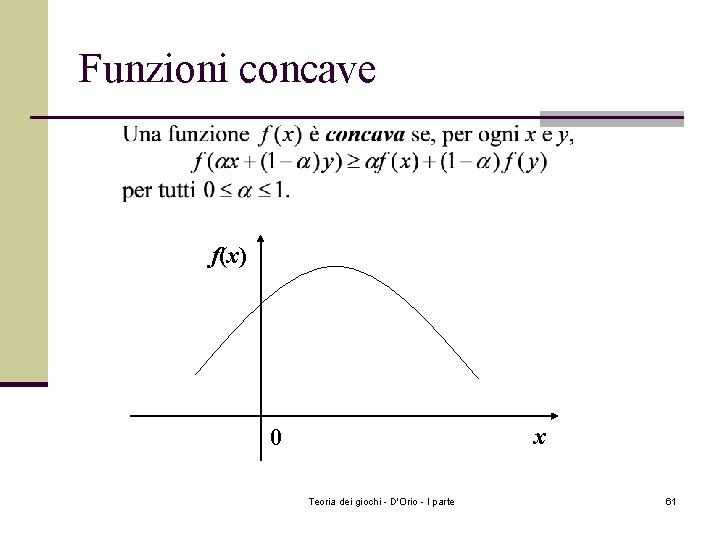
Funzioni concave f(x) x 0 Teoria dei giochi - D'Orio - I parte 61

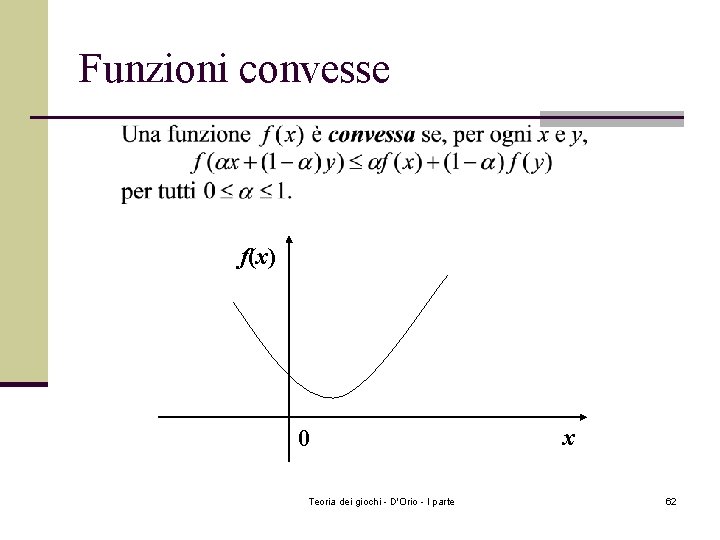
Funzioni convesse f(x) 0 Teoria dei giochi - D'Orio - I parte x 62

Concavità e convessità Teoria dei giochi - D'Orio - I parte 63

Concavità e convessità Teoria dei giochi - D'Orio - I parte 64

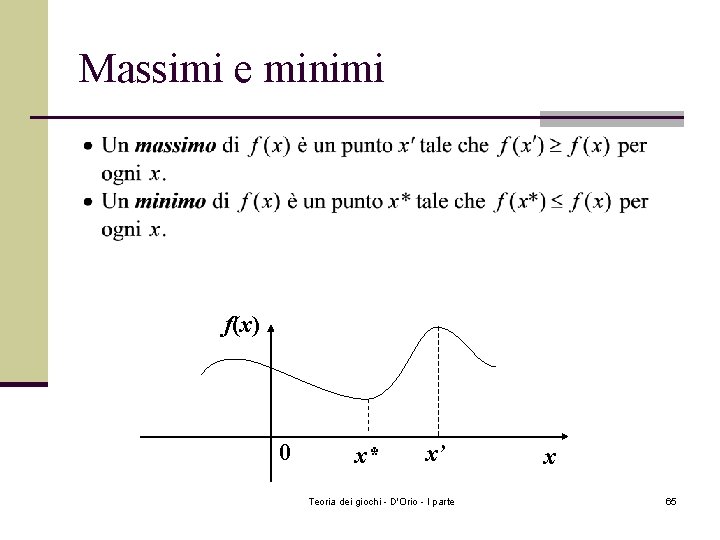
Massimi e minimi f(x) 0 x* x’ Teoria dei giochi - D'Orio - I parte x 65

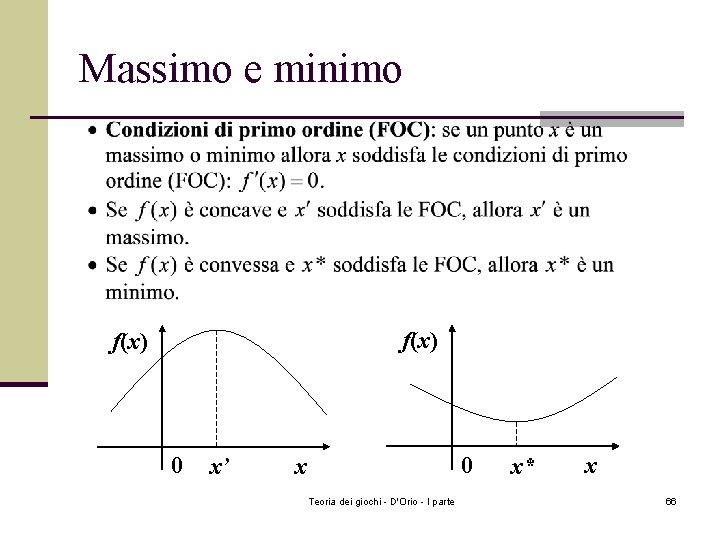
Massimo e minimo f(x) 0 x’ 0 x Teoria dei giochi - D'Orio - I parte x* x 66

Trovare il massimo di una funzione concava Teoria dei giochi - D'Orio - I parte 67

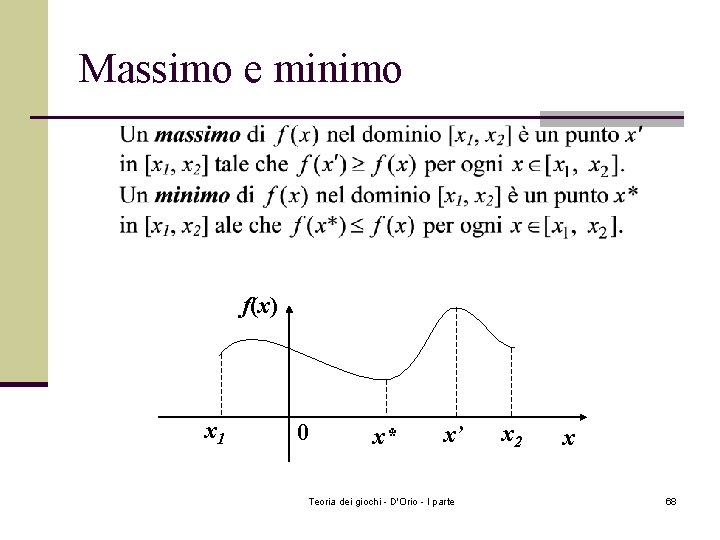
Massimo e minimo f(x) x 1 0 x* x’ Teoria dei giochi - D'Orio - I parte x 2 x 68

Trovare il massimo di una funzione concava con vincoli Teoria dei giochi - D'Orio - I parte 69

Trovare il massimo di una funzione concava con vincoli Teoria dei giochi - D'Orio - I parte 70

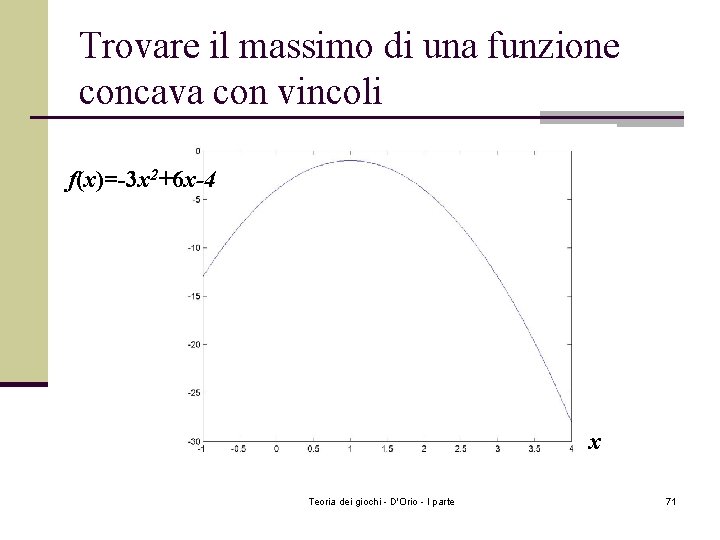
Trovare il massimo di una funzione concava con vincoli f(x)=-3 x 2+6 x-4 x Teoria dei giochi - D'Orio - I parte 71

Utilizzo della funzione di risposta ottima per la ricerca dell’equilibrio di Nash n In un gioco a due gioc. , ( s 1, s 2 ) è un equilibrio di Nash se e solo se la strategia s 1 del gioc. 1 è la rsipsota ottima alla strategia s 2 del gioc. 2, e se la strategia s 2 del giocatore 2 è la risposta ottima alla strategia s 1 del giocatore 1 Prig. 2 Nega Prig. 1 Nega Confessa -1 , -1 0 , -9 Teoria dei giochi - D'Orio - I parte Confessa -9 , 0 -6 , -6 72

Il modello del duopolio di Cournot n Come trovare l’equilibrio di Nash: n Trovate la coppia di quantità (q 1*, q 2*) tale che q 1* sia la risposta ottima dell’impresa 1 alla quantità q 2* dell’impresa 2 e q 2* sia la risposta ottima dell’impresa 2 alla quantità q 1* dell’impresa 1 n Ciò significa che, q 1* risolve Max u 1(q 1, q 2*)=q 1(a-(q 1+q 2*)-c) soggetto a 0 q 1 +∞ e q 2* risolve Max u 2(q 1*, q 2)=q 2(a-(q 1*+q 2)-c) soggetto a 0 q 2 +∞ Teoria dei giochi - D'Orio - I parte 73

Il modello del duopolio di Cournot n Ricerca dell’equilibrio di Nash Ø Risolvete Max u 1(q 1, q 2*)=q 1(a-(q 1+q 2*)-c) s. a 0 q 1 +∞ FOC: a - 2 q 1 - q 2*- c = 0 q 1 = (a - q 2*- c)/2 Teoria dei giochi - D'Orio - I parte 74

Il modello del duopolio di Cournot n Ricerca dell’equilibrio di Nash Ø Risolvete Max u 2(q 1*, q 2)=q 2(a-(q 1*+q 2)-c) s. a 0 q 2 +∞ FOC: a - 2 q 2 – q 1* – c = 0 q 2 = (a – q 1* – c)/2 Teoria dei giochi - D'Orio - I parte 75

Il modello del duopolio di Cournot n Ricerca dell’equilibrio di Nash Ø La coppia (q 1*, q 2*) è un equilibrio di Nash se q 1* = (a – q 2* – c)/2 q 2* = (a – q 1* – c)/2 Ø Risolvere queste due equazioni ci dà: q 1* = q 2* = (a – c)/3 Teoria dei giochi - D'Orio - I parte 76

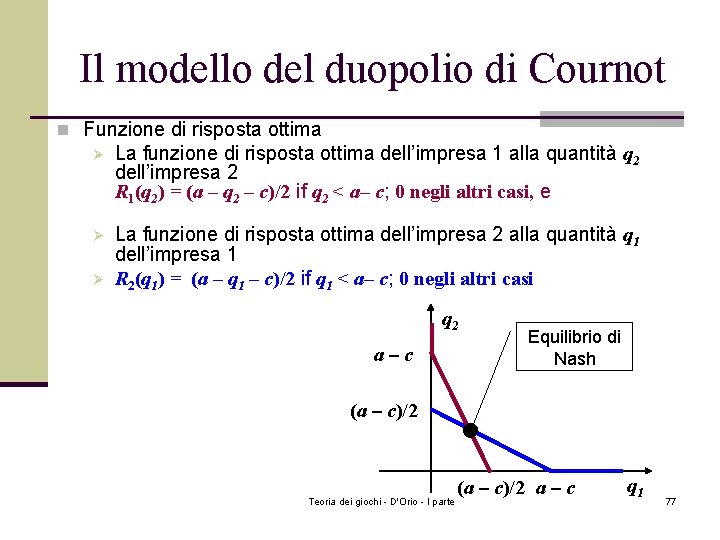
Il modello del duopolio di Cournot n Funzione di risposta ottima Ø La funzione di risposta ottima dell’impresa 1 alla quantità q 2 dell’impresa 2 R 1(q 2) = (a – q 2 – c)/2 if q 2 < a– c; 0 negli altri casi, e Ø La funzione di risposta ottima dell’impresa 2 alla quantità q 1 dell’impresa 1 R 2(q 1) = (a – q 1 – c)/2 if q 1 < a– c; 0 negli altri casi Ø q 2 a–c Equilibrio di Nash (a – c)/2 Teoria dei giochi - D'Orio - I parte (a – c)/2 a – c q 1 77

Il modello del duopolio di Cournot a n imprese n Un prodotto è realizzato da n imprese: dall’impresa 1 all’impresa n. La quantità dell’impresa i sia qi. Ogni impresa effettua la propria scelta senza sapere ciò che fanno le altre. n Il prezzo di mkt. è P(Q)=a-Q, dove a è una costante e Q=q 1+q 2+. . . +qn. n Il costo dell’impresa i di produrre la quantità qi è Ci(qi)=cqi. Teoria dei giochi - D'Orio - I parte 78

Il modello del duopolio di Cournot La rappresentazione in forma normale: Ø Insieme dei giocatori: { Impresa 1, . . . Impresa n} Ø Insieme delle strategie: Si=[0, +∞), per i=1, 2, . . . , n Ø Funzioni di payoff: ui(q 1 , . . . , qn)=qi(a-(q 1+q 2 +. . . +qn)-c) for i=1, 2, . . . , n Teoria dei giochi - D'Orio - I parte 79

Il modello del duopolio di Cournot n Come trovare l’equilibrio di Nash Ø Trovate le quantità (q 1*, . . . qn*) tali che qi* e la risposta ottima dell’impresa i alle quantità delle altre imprese. Ø Ciò significa che q 1* risolve Max u 1(q 1, q 2*, . . . , qn*)=q 1(a-(q 1+q 2* +. . . +qn*)-c) s. a 0 q 1 +∞ e q 2* risolve Max u 2(q 1*, q 2 , q 3*, . . . , qn*)=q 2(a-(q 1*+q 2+q 3*+. . . + qn*)-c) s. a 0 q 2 +∞. . . . Teoria dei giochi - D'Orio - I parte 80

Riassunto n Equilibrio di Nash n Funzioni concave e massimizzazione n Il modello del duopolio e dell’oligopolio di Cournot n Prossimo argomento n Il modello del duopolio di Bertrand Teoria dei giochi - D'Orio - I parte 81