Considere um cilindro oco cujas superfcies interna e

Considere um cilindro oco, cujas superfícies interna e externa estão expostas a fluidos com diferentes temperaturas. Considere: - Estado estacionário - Transferência de calor unidirecional (radial) - Sem geração de energia Transferência de Calor 1 – prof. Rodrigo Schlischting

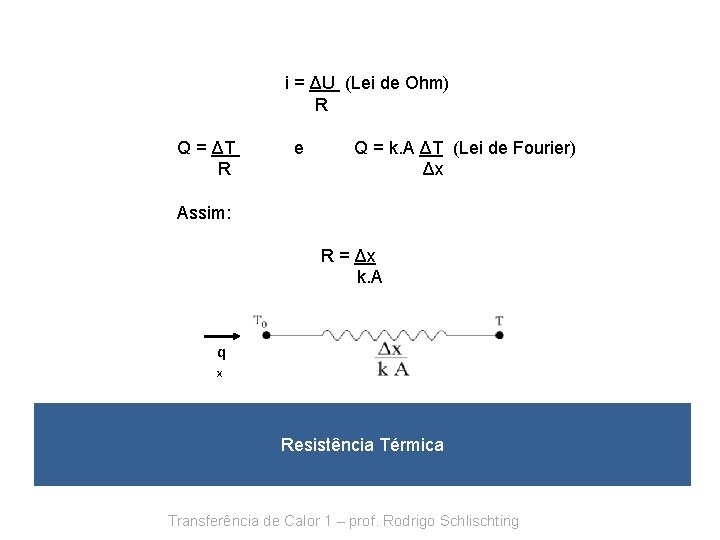
i = ΔU (Lei de Ohm) R Q = ΔT R e Q = k. A ΔT (Lei de Fourier) Δx Assim: R = Δx k. A q x Resistência Térmica Transferência de Calor 1 – prof. Rodrigo Schlischting

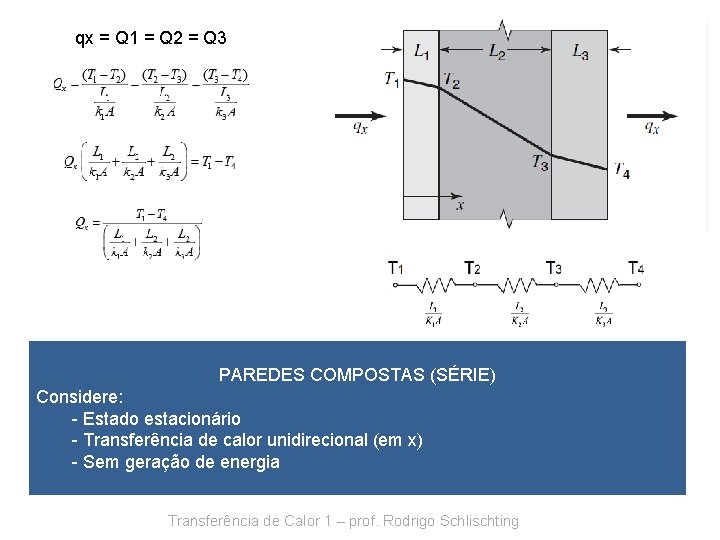
qx = Q 1 = Q 2 = Q 3 PAREDES COMPOSTAS (SÉRIE) Considere: - Estado estacionário - Transferência de calor unidirecional (em x) - Sem geração de energia Transferência de Calor 1 – prof. Rodrigo Schlischting

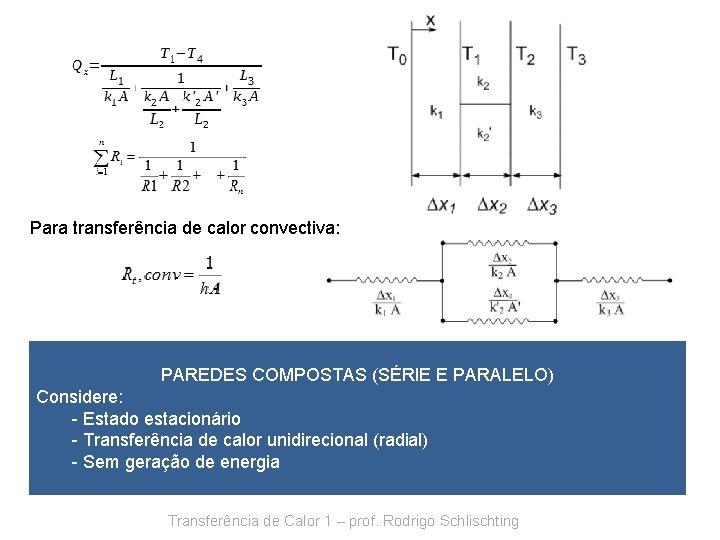
Para transferência de calor convectiva: PAREDES COMPOSTAS (SÉRIE E PARALELO) Considere: - Estado estacionário - Transferência de calor unidirecional (radial) - Sem geração de energia Transferência de Calor 1 – prof. Rodrigo Schlischting

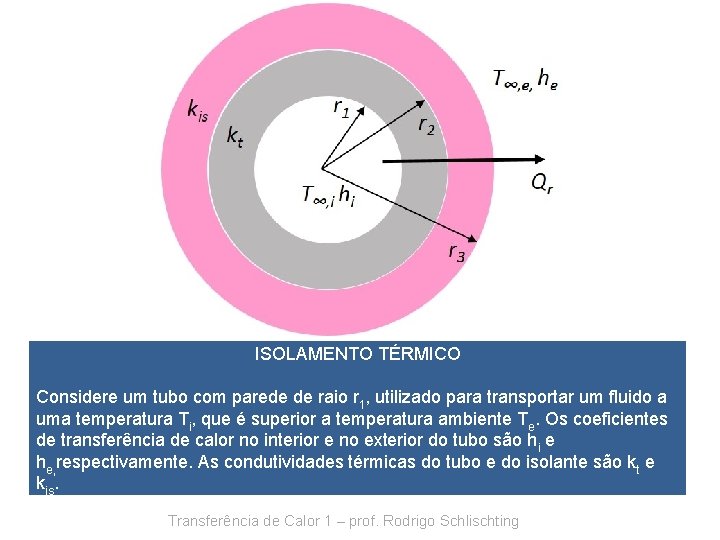
ISOLAMENTO TÉRMICO Considere um tubo com parede de raio r 1, utilizado para transportar um fluido a uma temperatura Ti, que é superior a temperatura ambiente Te. Os coeficientes de transferência de calor no interior e no exterior do tubo são hi e he, respectivamente. As condutividades térmicas do tubo e do isolante são kt e kis. Transferência de Calor 1 – prof. Rodrigo Schlischting

ISOLAMENTO TÉRMICO Considere: - Estado estacionário - Transferência de calor unidirecional (radial) - Sem geração de energia Transferência de Calor 1 – prof. Rodrigo Schlischting

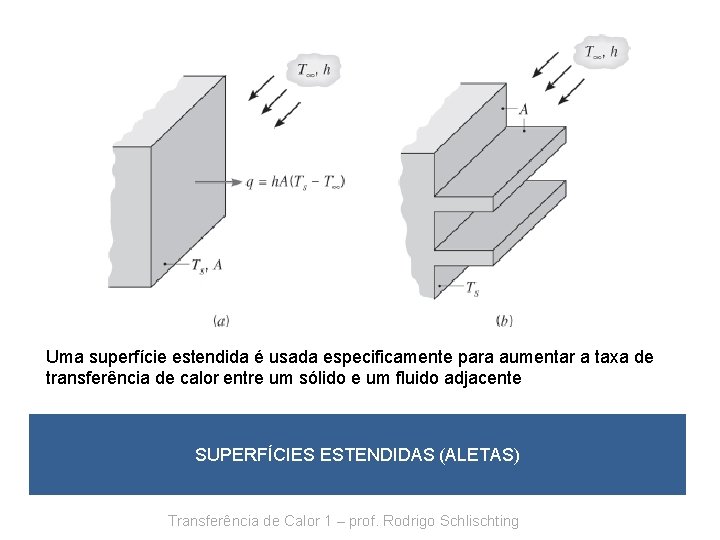
Uma superfície estendida é usada especificamente para aumentar a taxa de transferência de calor entre um sólido e um fluido adjacente SUPERFÍCIES ESTENDIDAS (ALETAS) Transferência de Calor 1 – prof. Rodrigo Schlischting

Configurações de aletas: (a) Aleta plana com seção transversal uniforme. (b) Aleta plana com seção transversal não uniforme. (c) Aleta anular. (d) Aleta piniforme. SUPERFÍCIES ESTENDIDAS (ALETAS) Transferência de Calor 1 – prof. Rodrigo Schlischting

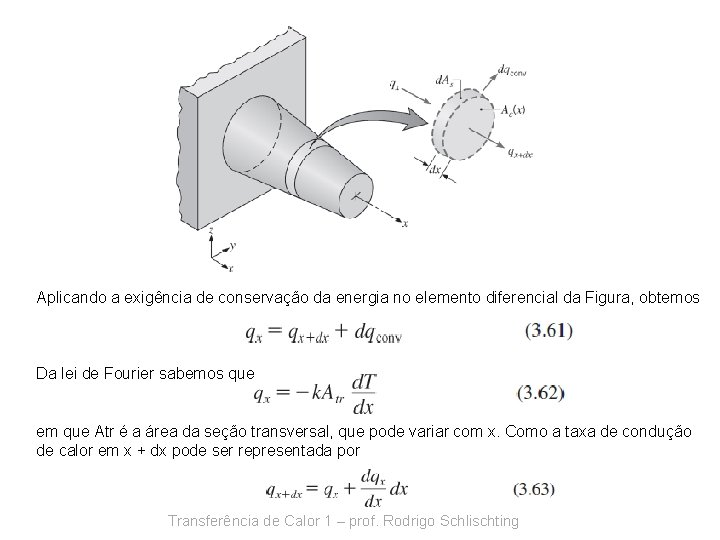
Aplicando a exigência de conservação da energia no elemento diferencial da Figura, obtemos Da lei de Fourier sabemos que em que Atr é a área da seção transversal, que pode variar com x. Como a taxa de condução de calor em x + dx pode ser representada por Transferência de Calor 1 – prof. Rodrigo Schlischting

tem-se que A taxa de transferência de calor por convecção pode ser representada por na qual d. As é a área superficial do elemento diferencial. Substituindo as equações de taxa anteriores no balanço de energia, Equação 3. 61, obtemos Ou (Equação da Energia para uma Superfície Estendida) Sua solução, com condições de contorno apropriadas, fornece a distribuição de temperaturas, que pode ser usada com a Equação 3. 62 (equação de Fourier) para calcular a taxa de condução em qualquer x. Transferência de Calor 1 – prof. Rodrigo Schlischting

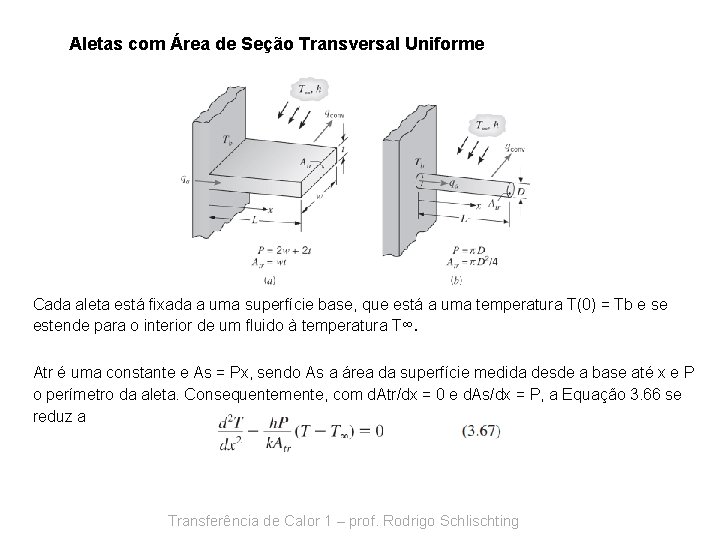
Aletas com Área de Seção Transversal Uniforme Cada aleta está fixada a uma superfície base, que está a uma temperatura T(0) = Tb e se estende para o interior de um fluido à temperatura T∞. Atr é uma constante e As = Px, sendo As a área da superfície medida desde a base até x e P o perímetro da aleta. Consequentemente, com d. Atr/dx = 0 e d. As/dx = P, a Equação 3. 66 se reduz a Transferência de Calor 1 – prof. Rodrigo Schlischting

Transformando a variável dependente definindo um excesso de temperatura θ como: Substituindo a Equação 3. 68 na Equação 3. 67 temos: Onde: A Equação 3. 69 é uma equação diferencial de segunda ordem, linear e homogênea, com coeficientes constantes. Sua solução geral é: Condições de Contorno: 1) temperatura na base da aleta (x = 0) Transferência de Calor 1 – prof. Rodrigo Schlischting

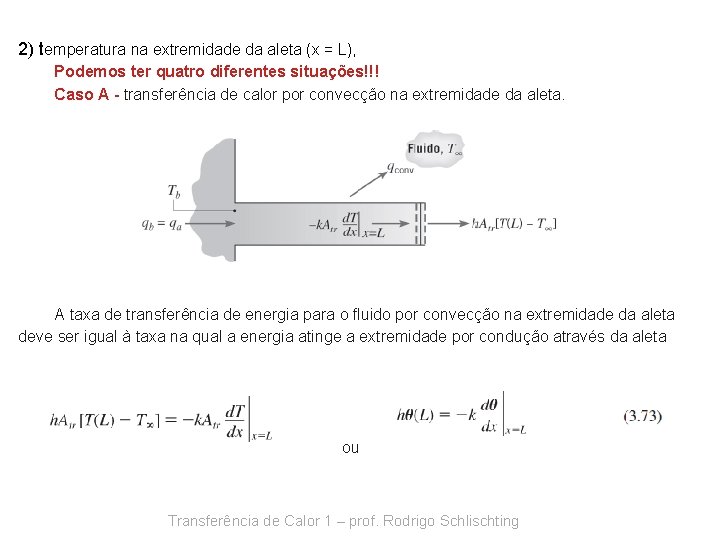
2) temperatura na extremidade da aleta (x = L), Podemos ter quatro diferentes situações!!! Caso A - transferência de calor por convecção na extremidade da aleta. A taxa de transferência de energia para o fluido por convecção na extremidade da aleta deve ser igual à taxa na qual a energia atinge a extremidade por condução através da aleta ou Transferência de Calor 1 – prof. Rodrigo Schlischting

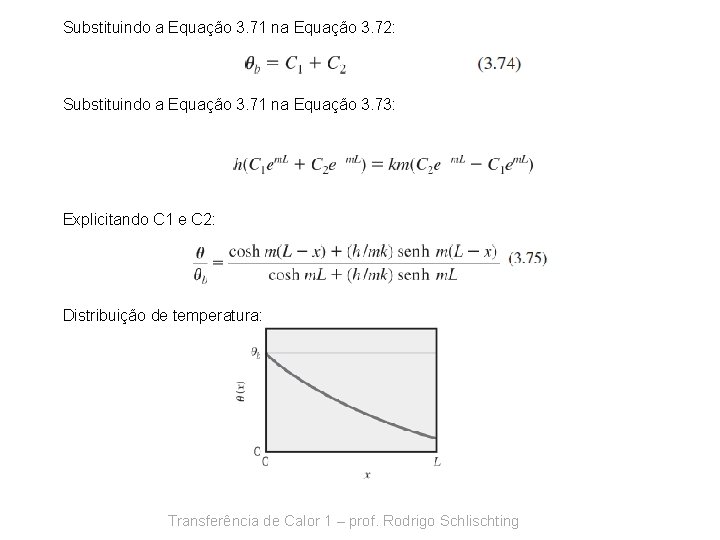
Substituindo a Equação 3. 71 na Equação 3. 72: Substituindo a Equação 3. 71 na Equação 3. 73: Explicitando C 1 e C 2: Distribuição de temperatura: Transferência de Calor 1 – prof. Rodrigo Schlischting

aplicando da lei de Fourier na base da aleta: Conhecendo-se a distribuição de temperatura temos: Caso B - a perda de calor por convecção na extremidade da aleta é desprezível (adiabática) Combinando com a equação 3. 71, temos C 1 em. L − C 2 e–m. L = 0 Substituindo na equação 3. 74 e explicitando C 1 e C 2: Transferência de Calor 1 – prof. Rodrigo Schlischting

Utilizando a distribuição de temperatura na Equação 3. 76 Caso C - temperatura na extremidade da aleta é especificada. Ou seja, a segunda condição de contorno é θ(L) = θL. Caso D – aleta muito longa, condição de contorno 2 é L → ∞, θL → 0 Transferência de Calor 1 – prof. Rodrigo Schlischting

Transferência de Calor 1 – prof. Rodrigo Schlischting

Desempenho de Aletas Aumentar a taxa de transferência de calor: Área superficial Resistência condutiva Efetividade da aleta εa - razão entre a taxa de transferência de calor na aleta e a taxa de transferência de calor que existiria sem a presença da aleta. ( εa ≥ 2) Resistência térmica da aleta Assim: Transferência de Calor 1 – prof. Rodrigo Schlischting

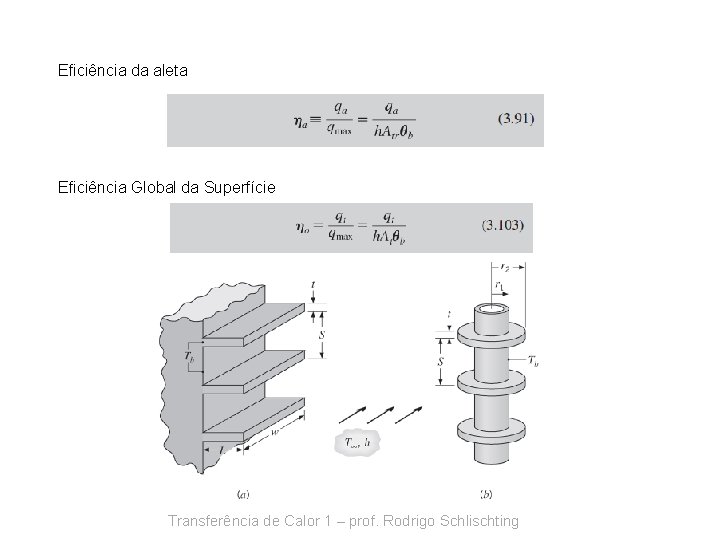
Eficiência da aleta Eficiência Global da Superfície Transferência de Calor 1 – prof. Rodrigo Schlischting

Substituindo a euquação 3. 106 na 3. 103 Transferência de Calor 1 – prof. Rodrigo Schlischting

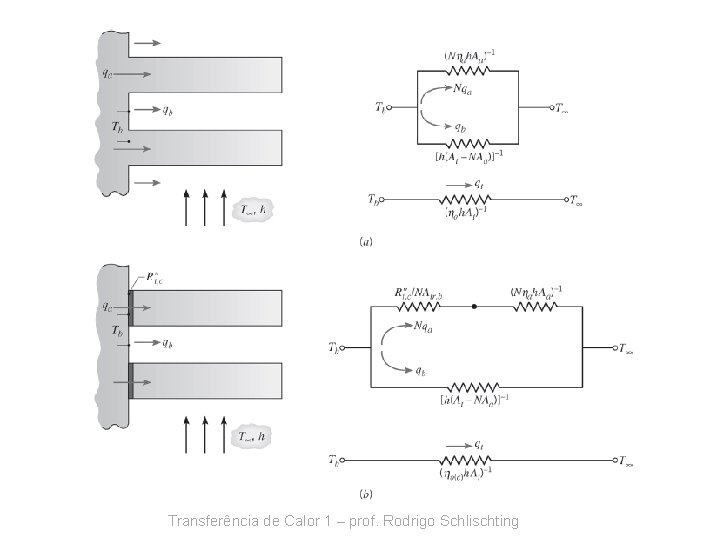
Resistência térmica de contato Assim: Onde: Na fabricação, deve-se tomar cuidado para garantir que Rt, c « Rt, a. Transferência de Calor 1 – prof. Rodrigo Schlischting

Transferência de Calor 1 – prof. Rodrigo Schlischting

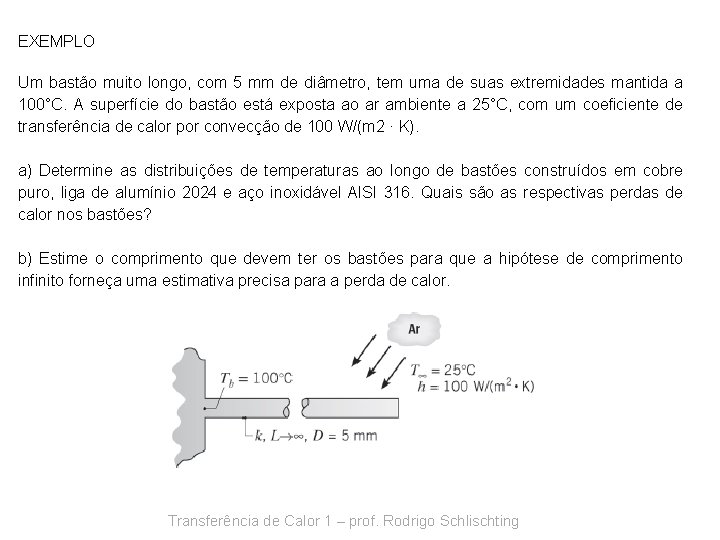
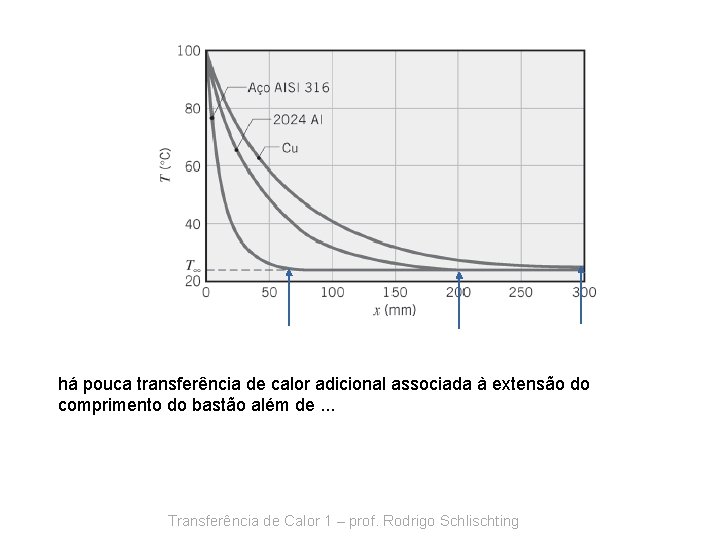
EXEMPLO Um bastão muito longo, com 5 mm de diâmetro, tem uma de suas extremidades mantida a 100°C. A superfície do bastão está exposta ao ar ambiente a 25°C, com um coeficiente de transferência de calor por convecção de 100 W/(m 2 · K). a) Determine as distribuições de temperaturas ao longo de bastões construídos em cobre puro, liga de alumínio 2024 e aço inoxidável AISI 316. Quais são as respectivas perdas de calor nos bastões? b) Estime o comprimento que devem ter os bastões para que a hipótese de comprimento infinito forneça uma estimativa precisa para a perda de calor. Transferência de Calor 1 – prof. Rodrigo Schlischting

Considerações: 1. Condições de regime estacionário. 2. Condução unidimensional ao longo do bastão. 3. Propriedades constantes. 4. Troca radiante com a vizinhança desprezível. 5. Coeficiente de transferência de calor uniforme. 6. Bastão comprimento infinito. Propriedades: Tabela A. 1, cobre [T = (Tb + T∞)/2 = 62, 5°C < 335 K]: k = 398 W/(m · K). Tabela A. 1, alumínio 2024 (335 K): k = 180 W/(m · K). Tabela A. 1, aço inoxidável, AISI 316 (335 K): k = 14 W/(m · K). Transferência de Calor 1 – prof. Rodrigo Schlischting

Definição: Caso D – aleta muito longa, condição de contorno 2 é L → ∞, θL → 0 Substituindo 3. 68 e 3. 72 na 3. 84, temos Onde: m = (h. P/k. Atr)1/2 = (4 h/k. D)1/2 Substituindo os valores do coeficiente de convecção [h = 100 W/m 2 K], do diâmetro da aleta [D = 5 mm], da condutividade térmica do cobre [k = 398 W/(m · K)], da liga de alumínio [k = 180 W/(m · K] e do aço inoxidável [k = 14 W/(m · K)], respectivamente, os valores de m são 14, 2; 21, 2 e 75, 6 m− 1 Lembrando que T∞ = 25ºC e Tb = 100ºC Transferência de Calor 1 – prof. Rodrigo Schlischting

há pouca transferência de calor adicional associada à extensão do comprimento do bastão além de. . . Transferência de Calor 1 – prof. Rodrigo Schlischting

Da equação 3. 85 Onde: P = πD e Atr = πD 2/4 Para o cobre temos: qa= [100. π. 0, 005. 398. (π/4). (0, 005)2]1/2 (100 -25) = 8, 3 W Para o alumínio temos: qa= [100. π. 0, 005. 180. (π/4). (0, 005)2]1/2 (100 -25) = 5, 6 W Para o aço temos: qa= [100. π. 0, 005. 14. (π/4). (0, 005)2]1/2 (100 -25) = 1, 6 W Transferência de Calor 1 – prof. Rodrigo Schlischting

Para um resultado preciso, (Caso D): θ(L) = T(L) – T∞ = e−m. L < 0, 01 θb θb Para o cobre: L∞ = (- ln 0, 01)/ 14, 2 = 0, 33 m Para o alumínio: L∞ = (- ln 0, 01)/ 21, 2 = 0, 22 m Para o aço: L∞ = (- ln 0, 01)/ 75, 6 = 0, 06 m Transferência de Calor 1 – prof. Rodrigo Schlischting

Aproximação: como não há perda de calor na extremidade de um bastão infinitamente longo, uma estimativa pode ser feita pela comparação das Equações 3. 81 e 3. 85. Com uma aproximação satisfatória, as expressões fornecem resultados equivalentes se a tanh m. L ≥ 0, 99 ou m. L ≥ 2, 65. Assim, um bastão pode ser considerado de comprimento infinito se: Para o cobre: L∞ = 2, 65 {[398. (π/4). (0, 005)2 ]/ [100. π. 0, 005]}1/2 = 0, 19 m Para o alumínio: L∞ = 2, 65 {[180. (π/4). (0, 005)2 ]/ [100. π. 0, 005]}1/2 = 0, 13 m Para a aço: L∞ = 2, 65 {[14. (π/4). (0, 005)2 ]/ [100. π. 0, 005]}1/2 = 0, 04 m Transferência de Calor 1 – prof. Rodrigo Schlischting

Lista de Exercícios: INCROPERA 7 EDIÇÃO 3. 13 3. 18 3. 19 3. 57 3. 61 3. 79 3. 84 3. 117 3. 129 3. 132 Transferência de Calor 1 – prof. Rodrigo Schlischting