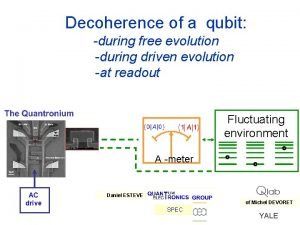
Classical Approach to Computing Quantum Decoherence Dynamics Paul

Classical Approach to Computing Quantum Decoherence Dynamics Paul Brumer Dept. of Chemistry, and Center for Quantum Information and Quantum Control University of Toronto

Original Motivation • For Decoherence: Possibility of controlling atomic and molecular processes via quantum interference (“coherent control”) • Ability of decoherence to destroy quantum effects, and hence destroy quantum control • Formal --Attempts to understand decoherence and entanglement (will not get to entanglement today…) --- since these are “quantum properties”

Specifically --- applications • Main: Determine decoherence rates in realistic systems, e. g. , molecules in solution • Hence: develop useful methods to evaluate decoherence in realistic systems ; these, as seen below, essentially classical (the classical analog approach) assess the utility of model master equation methods to quantitatively provide decoherence rates if valid, determine the correct Lindblad operator to describe decoherence in these systems • Then: Develop scenarios to counter decoherence in realistic systems

Essence of Coherent Control Original application AB + C ABC Control the ratio AC + B Basic principle (1) Construct two or more indistinguishable routes to the final state (2) Manipulate resultant interference via laboratory “knobs”

• Lots of applications done • But preservation of quantum mechanics required. Hence concern about loss of quantum effects via decoherence and concern about developing methods to counter decoherence effects.

Here: sketch of ongoing program • Decoherence computation via semiclassical • Perturbation and proof of utility of “classical analog” at short times and at all times for strong decoherence. • Numerical demo of validity over all time (small systems). • Application to I 2 in Liquid (Lennard-Jones) Xe. • Interesting observation on temperature dependence/bath chaos of decoherence (“Wilkie’s conjecture”).

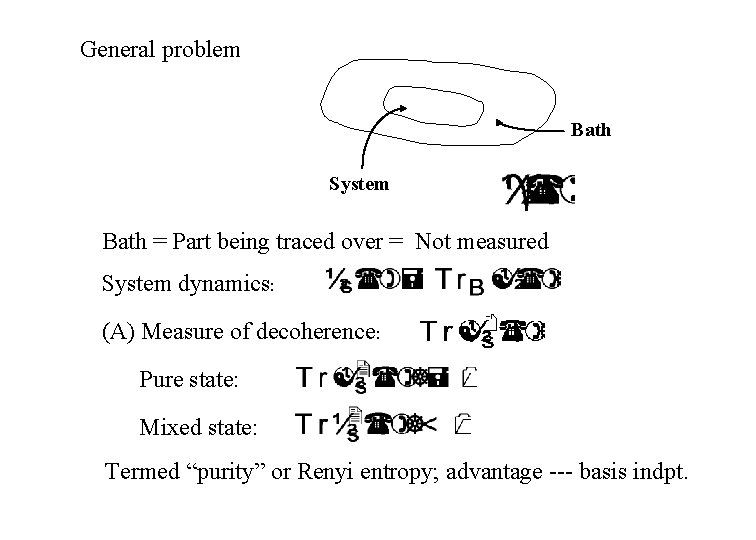
General problem Bath System Bath = Part being traced over = Not measured System dynamics: (A) Measure of decoherence: Pure state: Mixed state: Termed “purity” or Renyi entropy; advantage --- basis indpt.

E. g. for two levels: Both two level as well as multilevel examined below Includes two effects, but here Interested in short time where population changes are small. Also: time dependence of , in (basis dependent) energy eigenstates of the system.

First look; Semiclassical IVR (Elran and Brumer, JCP 121, 2673, 2004) Sample system: I 2 linearly coupled to an harmonic oscillator bath (Bill Miller’s group--- Wang et al, JCP 114, 2562, 2001): Parameters qualitative. v

Semiclassical IVR Approach • Consider time correlation function: • To obtain for system in thermal bath, choose Propagate using semiclassical forward-backward Initial Value Representation

“Zeno effect” Recurrences Fig. 1: Decoherence dynamics: Purity as a function of time for the multilevel coherent state. T = 300 K, = 0. 25. Iodine in Harmonic bath. Note three regimes: And vast dependence on initial state.

nt state 6 -level cohere 2 -level superposition CAT 60 -level coherent state Note times Figure 5: Purity as a function of times for different initial states at T = 300 K, = 0. 25. cat state (solid line), multilevel coherent state (dotted line), six-level coherent state (dashed line), superposition state (dotted-dashed line).

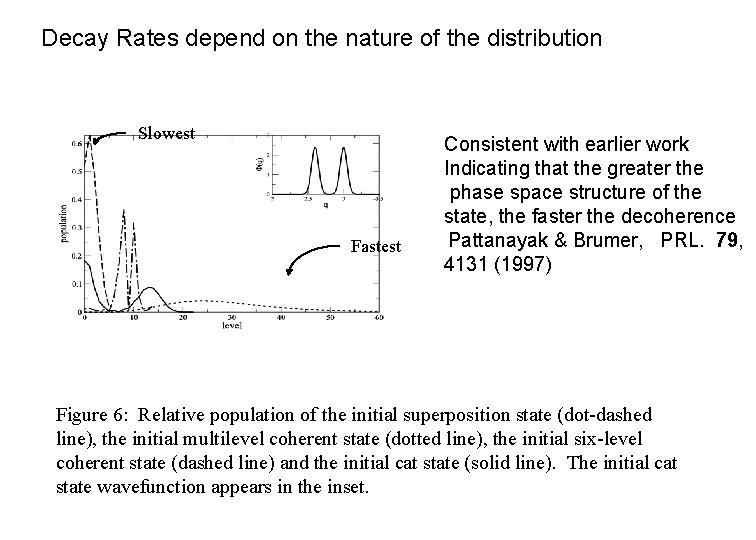
Decay Rates depend on the nature of the distribution Slowest Fastest Consistent with earlier work Indicating that the greater the phase space structure of the state, the faster the decoherence Pattanayak & Brumer, PRL. 79, 4131 (1997) Figure 6: Relative population of the initial superposition state (dot-dashed line), the initial multilevel coherent state (dotted line), the initial six-level coherent state (dashed line) and the initial cat state (solid line). The initial cat state wavefunction appears in the inset.

Computations successful but very intensive. Possible approximations? Here look at two directions to a classical (analog) approach 1. Perturbative argument 2. Classical analog (linearized IVR)

Classical Analog • Recall correlation function structure for : • In general, we have some correlation function of the form C(t) = Tr [ B(t) A(0)] = Tr [ BW(t) AW(0)] Classical Analog: Propagate BW(t) classically, even if distribution is negative Application here: Start with Quantum system + bath, propagate dynamics classically and trace over bath

Long History Considerable work now using this type of approximation. Historically Classical analog: • Brumer and Jaffe, J. Chem. Phys. 82, 2330 (1985); Jaffe, Kanfer and Brumer, Phys. Rev. Lett. 54, 8, (1985); Wilkie & Brumer, Phys. Rev. A 55, 27 (1997); Wilkie & Brumer, Phys. Rev. A 55, 43 (1997) Linearized semiclassical IVR l: Wang, Sun and Miller, J. Chem. Phys. 108, 9726 (1998); Sun and Miller, J Chem. Phys. 110, 6635 (1999); Shao, Liao and Pollak, J. Chem. Phys. 108, 9711 (1998)

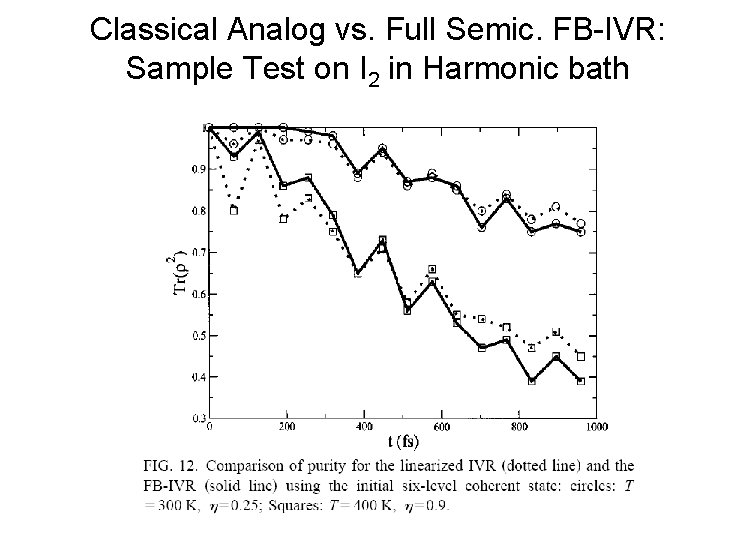
Classical Analog vs. Full Semic. FB-IVR: Sample Test on I 2 in Harmonic bath

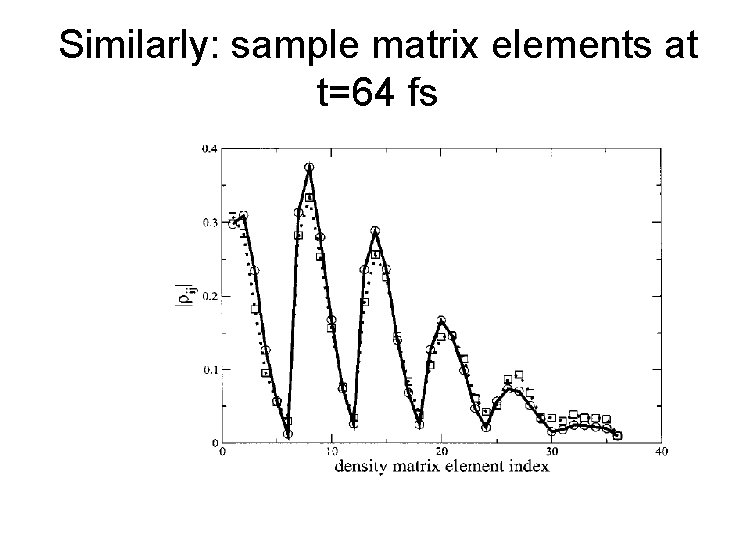
Similarly: sample matrix elements at t=64 fs

In support of this approximation--- conceptual and practical for decoherence (and entanglement) computations Quantum Mechanics --- (drop s subscript throughout) Density ; Phase-space rep’n Dynamics One of several complete phase space repn’s of quantum dynamics Classical mechanics: Density Dynamics Poisson Bracket Conceptual: Note beautiful classical/quantum analog:

E. G. Can define Eigenfunctions, Eigenvalues, etc. of time evolution OP (Liouville OP) etc. Hilbert space, etc. – e. g. , Koopmans, Prigogine (Our) Prior applications Quantum classical correspondence: Jaffe & Brumer, J. Chem. Phys. 82, 2330 (1985) Wilkie & Brumer, Phys. Rev. A 55, 27 (1997) Wilkie & Brumer, Phys. Rev. A 55, 43 (1997) Classical analog of superposition state: Jaffe, Kanfer & Brumer, Phys. Rev. Lett. 54, 8 (1985)

Support --- formal Consider, for simplicity, one-D system coupled to harmonic bath: (1) Coupling: Gen’l possible System coordinate N. B. f(Q) can be linear or nonlinear common (2) Define reduced system density, both class. + quant. (3) Measures of decoherence (sample) (4) Linear entropy (5) Quantal (6) Classical

(b) Off-diagonal Matrix Element Definition: Quantum Classical ! Possible treatments (A) Exact dynamics (B) Perturbative for short time Importance for decoherence control (C) Strong decoherence for all time Quantum computing Perturbation theory

where Recall (time zero) Hence: The sole difference between quantum and classical (perturbative – short time) is i. e. , Note result applicable to any coupling f(Q)

eira-Leggett Qualitative consequences (1) If Cald E. g. , Zurek / then i. e. , classical is exact for linear + quadratic system-bath coupling! Of course, but. . . (2) For any that ; wherever then class quant. (3) For any nonlinear/nonquadratic quant. decays fast enough with ΔQ so , then class

For longer time? Can do strong decoherence case (i. e. , Hs ~ 0) and obtain both And again all expressions, including phases are See: J. Gong & P. Brumer, Phys. Rev. Lett. 90, 050402 (2003) J. Gong & P. Brumer, Phys. Rev. A 68, 022101 (2003)

Hence, if you set up an initial superposition state, the subsequent decoherence dynamics is Short time (1) Classical if coupling (2) Classical for any coupling if over (3) Nonclassical if NOT (1) or (2) All time: Strong decoherence As above Even if the state is nonclassical Can we use to compute, etc ? Sample intrinsic decoherence case

But what about dynamics over longer times? Try sample simple systems E. g. , Two types of Quartic oscillator ; Integrable ; Chaotic Highly nonlinear Note: Zeroth order is not harmonic oscillators

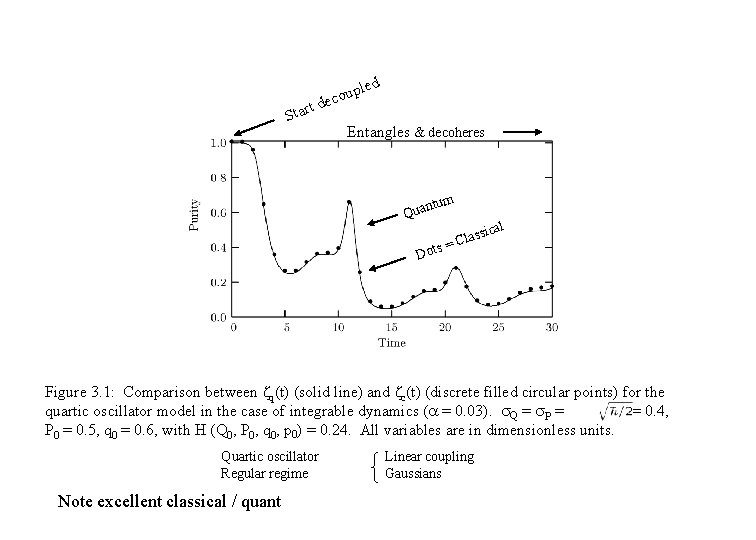
led t Star up o c e d Entangles & decoheres ntum Qua Dots assi = Cl cal Figure 3. 1: Comparison between ζq(t) (solid line) and ζc(t) (discrete filled circular points) for the quartic oscillator model in the case of integrable dynamics ( = 0. 03). Q = P = , Q 0 = 0. 4, P 0 = 0. 5, q 0 = 0. 6, with H (Q 0, P 0, q 0, p 0) = 0. 24. All variables are in dimensionless units. Quartic oscillator Regular regime Note excellent classical / quant Linear coupling Gaussians

Quantum Classical t=0 t=5 t = 10 Same in energy basis t = 15 Figure 3. 37: Time evolution of in energy representation for the integrable case considered in Fig. 3. 1. The left (right) panels correspond to the quantum (classical) system.

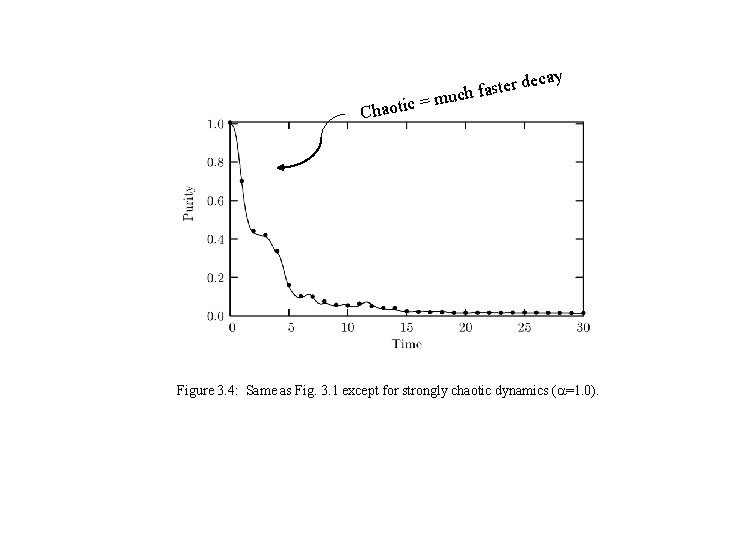
c=m Chaoti ecay ter d uch fas Figure 3. 4: Same as Fig. 3. 1 except for strongly chaotic dynamics ( =1. 0).

Quantum Classical t=0 t=5 t = 10 t = 15 Figure 3. 38: Time evolution of in energy representation for the chaotic case considered in Fig. 3. 4. The left (right) panels correspond to the quantum (classical) system.

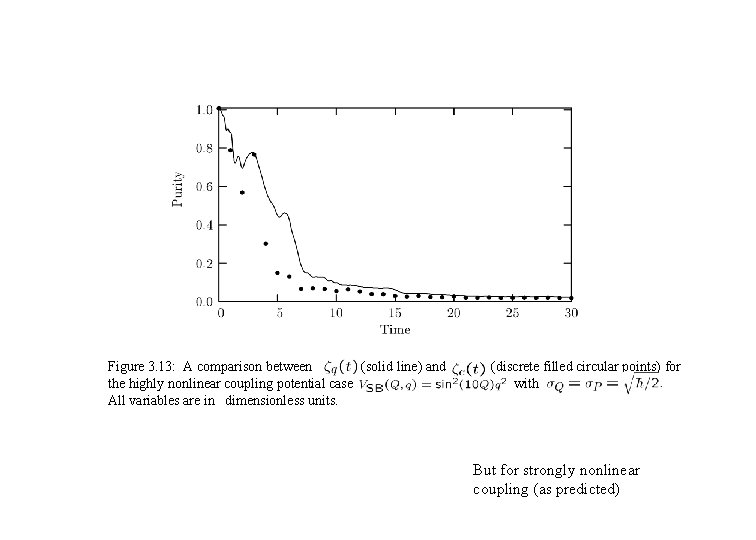
Figure 3. 13: A comparison between (solid line) and the highly nonlinear coupling potential case All variables are in dimensionless units. (discrete filled circular points) for with But for strongly nonlinear coupling (as predicted)

Realistic System: Application to Breathing Sphere I 2 in Lennard-Jones Bath • Model due to Egorov and Skinner, JCP 105, 7047 (1996) • Compute both and in energy basis; times far shorter than T 1

Computational approach • Thermalize bath (from 23 to 824 particles) • Set up initial wavefunction for I 2, compute associated Wigner function, propagate using classical mechanics • Produce system by ignoring other variables ( = averaging).

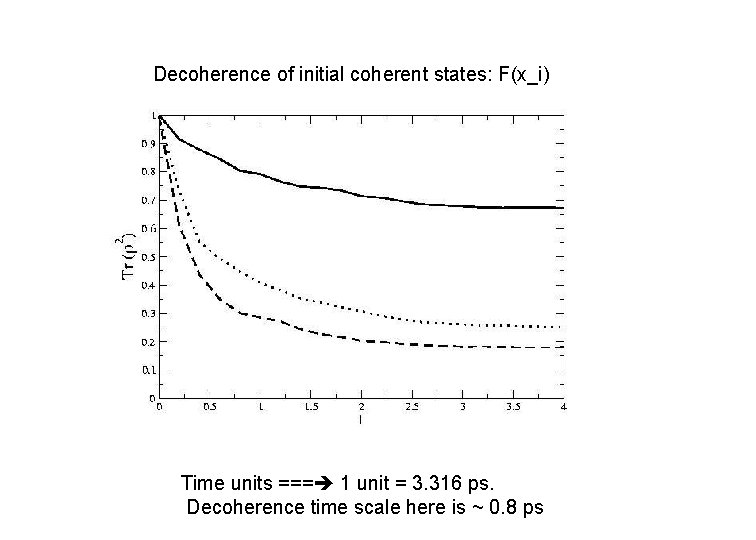
Decoherence of initial coherent states: F(x_i) Time units === 1 unit = 3. 316 ps. Decoherence time scale here is ~ 0. 8 ps

Correlates well with “size” of coherent state. Also predicts harmonic oscillator slower decay

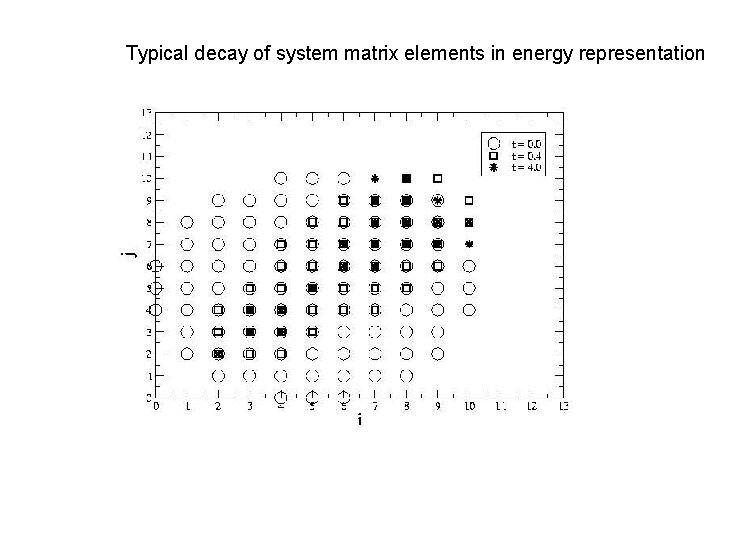
Typical decay of system matrix elements in energy representation

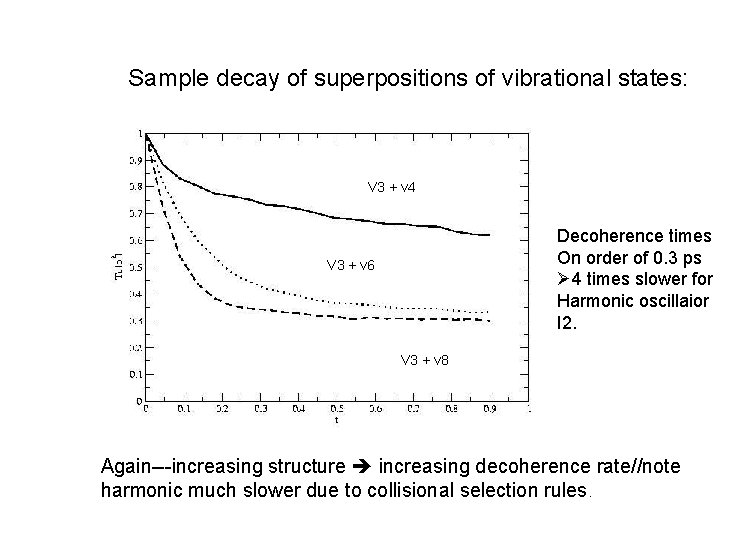
Sample decay of superpositions of vibrational states: V 3 + v 4 Decoherence times On order of 0. 3 ps Ø 4 times slower for Harmonic oscillaior I 2. V 3 + v 6 V 3 + v 8 Again---increasing structure increasing decoherence rate//note harmonic much slower due to collisional selection rules.

Does a simple Caldeira-Leggett model work? • Still computationally intensive, Can we replace by simple master equation. Try standard Caldeira-Leggett model: • System linearly coupled to an harmonic bath In high temperature, low coupling limit. Gives, for the Wigner function Where D is the coupling term How does Tr(rho^2) behave?

Can show directly • Consider Then can show directly that for this model that Hence, (1) d. S/dt increases with structure of The system (2) We can test Caldeira-Leggett utility by Computing terms and extracting D. Is it Constant, and of what size?

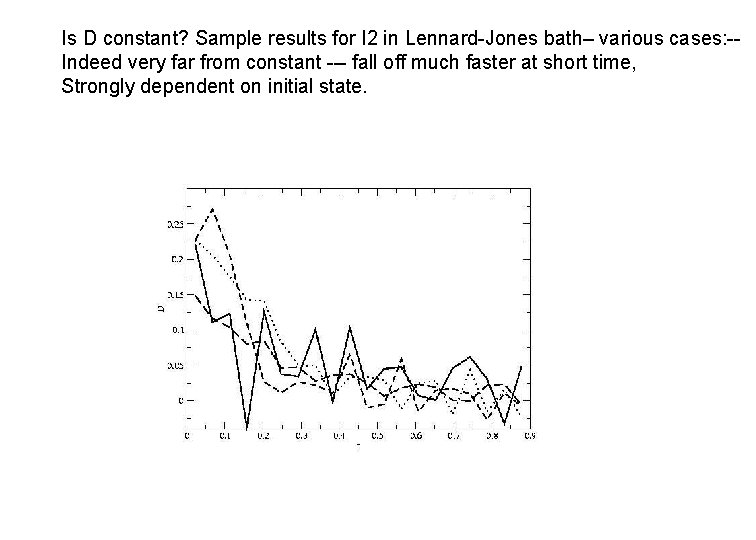
Is D constant? Sample results for I 2 in Lennard-Jones bath– various cases: -Indeed very far from constant --- fall off much faster at short time, Strongly dependent on initial state.

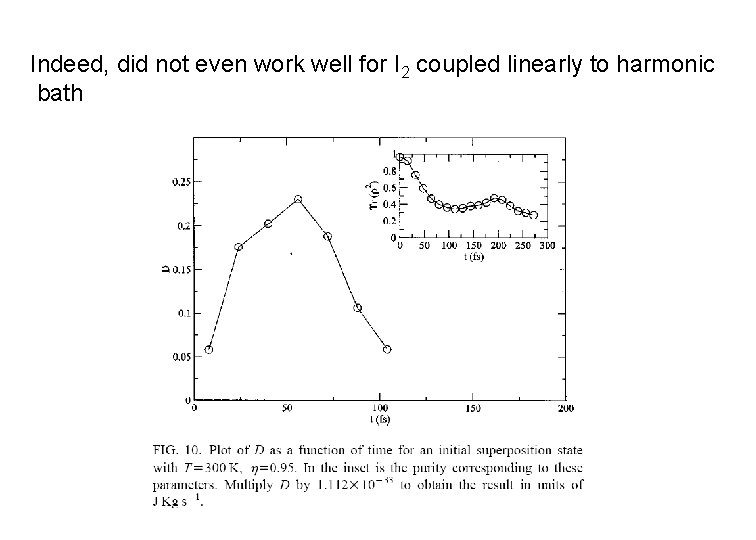
Indeed, did not even work well for I 2 coupled linearly to harmonic bath

Wilkie conjecture • Decoherence of system interacting with a chaotic bath is slower than that of a system in an uncoupled system --- at least at low temperature • Possible changeover in behavior at higher temperature to be consistent with others • Behavior confirmed for spin bath. But for collisional bath? • Can test by decoupling LJ bath.

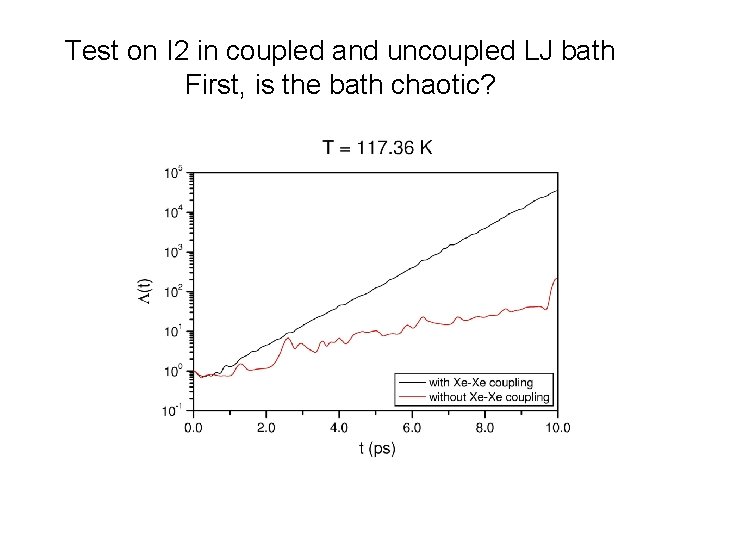
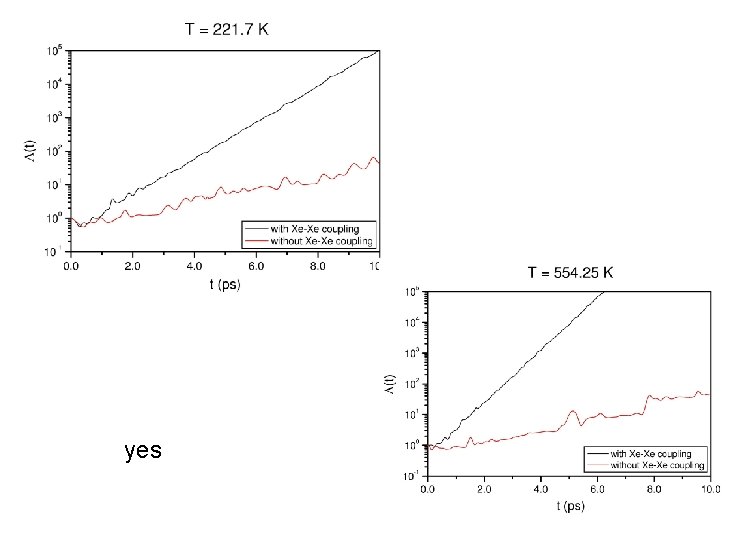
Test on I 2 in coupled and uncoupled LJ bath First, is the bath chaotic?

yes

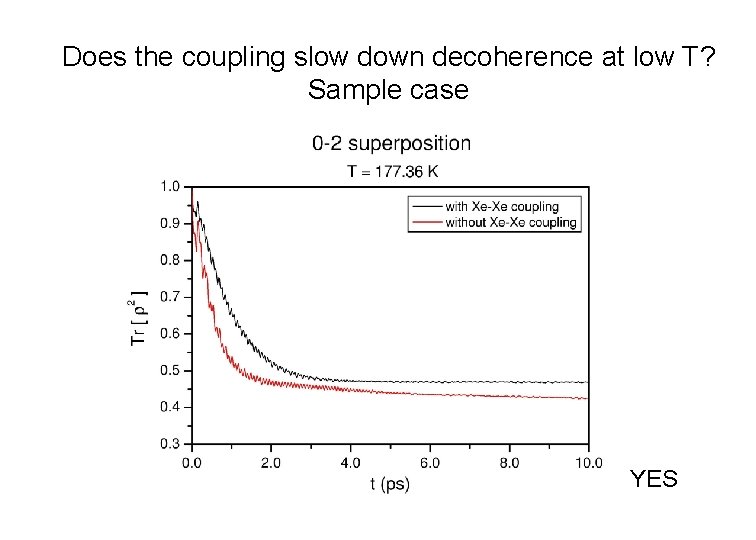
Does the coupling slow down decoherence at low T? Sample case YES

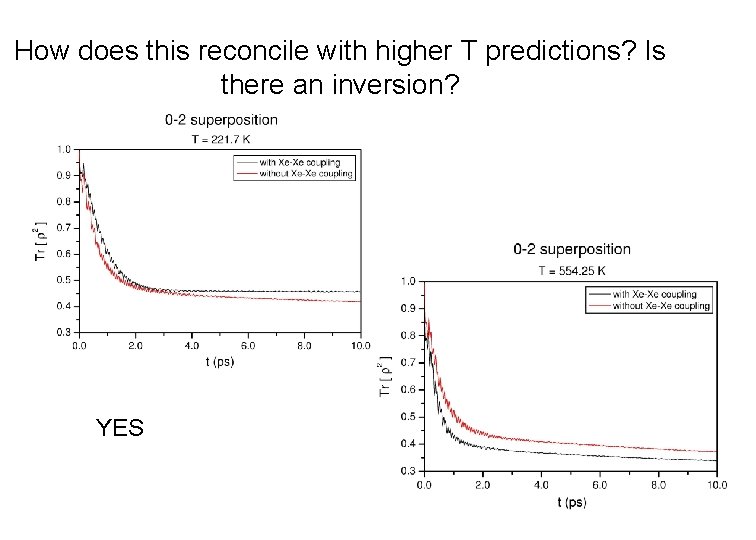
How does this reconcile with higher T predictions? Is there an inversion? YES

Summary • Decoherence can be efficiently computed using the classical analog approach • Relative decoherence rates are in accord with predictions based upon phase space structure. • The simple Caldeira-Leggett model unfortunately not useful in Iodine in liquid Xe. • Interesting behavior to explore, such as the reduction of decoherence at low temperatures upon strongly coupling up the bath.

THANKS TO: Dr. Yossi Elran (semiclassical decoherence and classical analog) Dr. Jiangbin Gong (theory and analytics ) Prof. Raymond Kapral (classical analog) Dr. Angel Sanz (Wilkie conjecture) Ms. Heekung Han (further studies) $$ ONR, Photonics Research Ontario NSERC$$