The Limits of Quantum Computers or What We
















![[A. , STOC’ 02] N 1/5 lower bound on quantum query complexity of the [A. , STOC’ 02] N 1/5 lower bound on quantum query complexity of the](https://slidetodoc.com/presentation_image/32c37f864ba7ba2a6c4bffa4c964b241/image-19.jpg)


![Bounded in [0, 1] at integer points 1 q(k) 0 Large derivative 1 k Bounded in [0, 1] at integer points 1 q(k) 0 Large derivative 1 k](https://slidetodoc.com/presentation_image/32c37f864ba7ba2a6c4bffa4c964b241/image-22.jpg)






![The Lemonade “Quantum Occam’s Razor Theorem” [A. 2006] | Upper bound on the sample The Lemonade “Quantum Occam’s Razor Theorem” [A. 2006] | Upper bound on the sample](https://slidetodoc.com/presentation_image/32c37f864ba7ba2a6c4bffa4c964b241/image-32.jpg)




- Slides: 36

The Limits of Quantum Computers (or: What We Can’t Do With Computers We Don’t Have) Scott Aaronson University of Waterloo SZK BQP NPcomplete

So then why can’t we just ignore quantum computing, and get back to real work?

Because the universe isn’t classical My picture of reality, as an eleven-year-old messing around with QBASIC: + details (Also Stephen Wolfram’s current picture of reality) Fancier version: Extended Church-Turing Thesis

Shor’s factoring algorithm presents us with a choice Either 1. the Extended Church-Turing Thesis is false, 2. textbook quantum mechanics is false, or That’s why YOU should care about 3. there’s an efficient classical factoring algorithm. quantum computing All three seem like crackpot speculations. At least one of them is true!

My Spiel In One Slide 1. Ignoring quantum mechanics won’t make it go away 2. Quantum computing is not a panacea—and that makes it more interesting rather than less! 3. On our current understanding, quantum computers could “merely” break RSA, simulate quantum physics, etc. —not solve generic search problems exponentially faster 4. So then why do I worry about quantum computing? Because I’m interested in fundamental limits on what can efficiently be computed in the physical world. That makes me professionally obligated to care!

Where Do I Come In? My work, over the last seven years, has deepened our understanding of the limitations of quantum computers. Solved some of the field’s notorious open problems: - Lower bound for finding collisions in hash functions - “Direct product theorem” for quantum search Made unexpected connections: - Classical lower bounds proved by quantum arguments - Quantum-state learning algorithm from a lower bound

Plan of Talk The Gospel According to Shor Three Limitations of Quantum Computers - Finding collisions in hash functions - Solving NP-complete problems with advice - Finding local optima Turning Lemons into Lemonade - Approximately learning quantum states Summary of Contributions

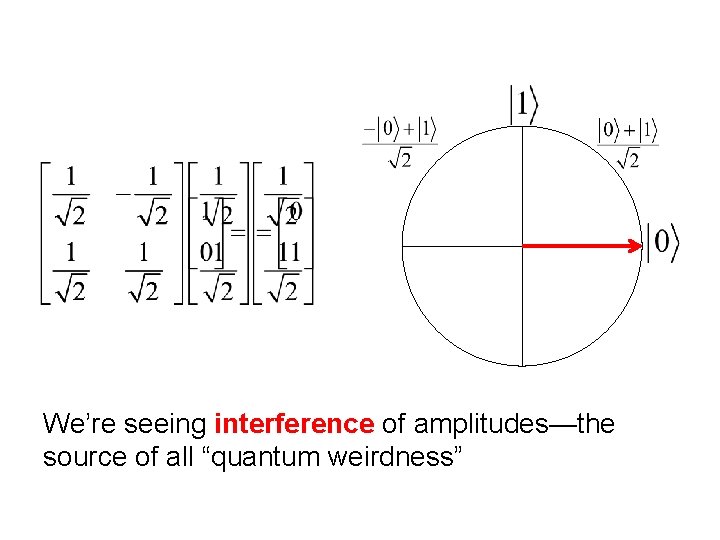
What Quantum Mechanics Says If an object can be in two distinguishable states |0 or |1 , then it can also be in a superposition |0 + |1 Here and are complex amplitudes satisfying | |2+| |2=1 If we observe, we see |0 with probability | |2 |1 with probability | |2 Also, the object collapses to whichever outcome we see

To modify a state we can multiply vector of amplitudes by a unitary matrix—one that preserves

We’re seeing interference of amplitudes—the source of all “quantum weirdness”

Quantum Computing A quantum state of n “qubits” takes 2 n complex numbers to describe: The goal of quantum computing is to exploit this exponentiality in our description of the world Idea: Get paths leading to incorrect answers to interfere destructively and cancel each other out

Plan of Talk The Gospel According to Shor Three Limitations of Quantum Computers - Finding collisions in hash functions - Solving NP-complete problems with advice - Finding local optima Turning Lemons into Lemonade - Approximately learning quantum states Summary of Contributions

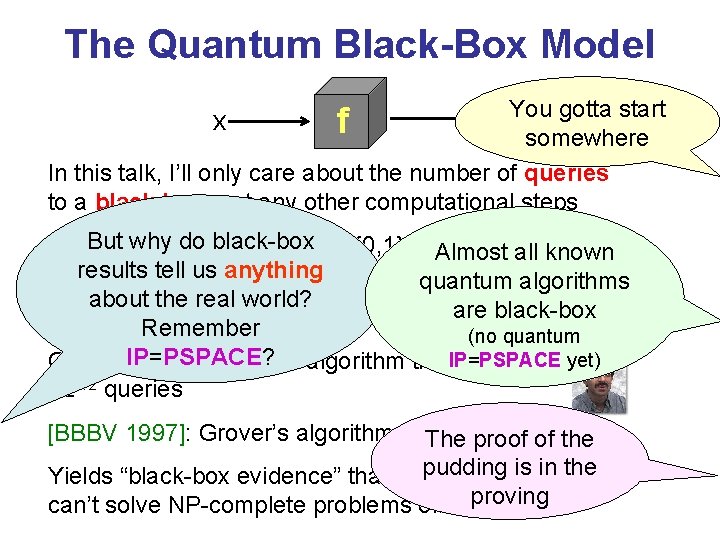
The Quantum Black-Box Model x f f(x)You gotta start somewhere In this talk, I’ll only care about the number of queries to a black box, not any other computational steps But why. Given do black-box Example: a function f: {0, 1}n {0, 1}, Almostsuppose all known us anything weresults want totell decide if there’s an x such that f(x)=1 quantum algorithms about the real world? are black-box n Classically, ~2 queries to f are needed Remember (no quantum Grover IP=PSPACE? gave a quantum algorithm that. IP=PSPACE uses only yet) ~2 n/2 queries [BBBV 1997]: Grover’s algorithm is The optimal proof of the pudding is in the Yields “black-box evidence” that quantum computers proving can’t solve NP-complete problems efficiently

Algorithm’s state: x: location to query w: “workspace” qubits After a query transformation: Between two queries, we can apply an arbitrary unitary matrix that doesn’t depend on f Complexity = minimum number of queries needed to achieve for all oracles f

Plan of Talk The Gospel According to Shor Three Limitations of Quantum Computers - Finding collisions in hash functions - Solving NP-complete problems with advice - Finding local optima Turning Lemons into Lemonade - Approximately learning quantum states Summary of Contributions

Problem: Find 2 numbers that are the same (each number appears twice) 28 32 31 69 57 20 49 56 37 68 60 55 12 18 76 96 82 94 99 21 78 88 93 39 44 64 99 By 70“birthday 18 94 66 paradox”, 92 64 95 a 46 53 16 35 42 72 66 randomized 75 33 93 algorithm 32 47 17 must 70 37 78 79 36 63 40 92 71 28 N 85 of 41 73 63 95 57 43 84 67 examine the 80 N 10 numbers 31 62 39 65 74 24 90 26 83 60 91 27 96 35 26 52 88 89 38 97 54 30 62 79 71 84 50 38 [Brassard-Høyer-Tapp Is that optimal? 20 47 24 54 48 98 23 41 16 40 75 82 13 58 1997] Quantum Proving a lower 81 34 14 61 52 21 44 22 34 14 51 74 76 83 algorithm based on bound 90 58 13 10 25 29 11 56 68 12 better 61 51 than 23 77 Grover that 46 uses only 45 59 constant 72 43 69 87 97 73 30 19 was 81 open 86 49 1/3 for 548 years 85 80 N 50 queries 11 59 65 67 89 29 86 22 15 17 36 27 42 55 77 19 45 15 53 98 91 87 25 33

Motivation for the Collision Problem Cryptographic Hash Functions Graph Isomorphism: find a collision in ? Statistical Zero Knowledge (SZK) protocols

What makes the problem so hard? Basically, that a quantum computer can almost find a collision after one query! Measure 2 nd register “If only we could now measure twice!” Or: if only we could see the whole trajectory of a “hidden variable” coursing through the quantum system! [A. , Phys. Rev. A 2005] Previous techniques weren’t sensitive to the fact that quantum mechanics doesn’t allow these things
![A STOC 02 N 15 lower bound on quantum query complexity of the [A. , STOC’ 02] N 1/5 lower bound on quantum query complexity of the](https://slidetodoc.com/presentation_image/32c37f864ba7ba2a6c4bffa4c964b241/image-19.jpg)
[A. , STOC’ 02] N 1/5 lower bound on quantum query complexity of the collision problem [Shi, FOCS’ 02] Improved to N 1/3; also [A. -Shi, J. ACM 2004] N 2/3 lower bound for element distinctness [Kutin 2003] Simplifications and [Ambainis 2003] generalizations [Midrijanis 2003]

Cartoon Version of Proof T-query quantum algorithm that finds collisions in 2 -to-1 functions Suppose it exists by way of contradiction… T-query quantum algorithm that distinguishes 1 -to-1 from 2 -to-1 functions Let p(f) = probability algorithm says f is 2 -to-1 Let q(k) = average of p(f) over all k-to-1 functions f [Beals et al. 1998] p(f) is a multilinear polynomial, of degree at most 2 T, in Boolean indicator variables (f(x), y) Trivial yet crucial facts: q(k) [0, 1] for all k=1, 2, 3, … q(1) 1/3 q(2) 2/3

The magic step: q(k) itself is a univariate polynomial in k, of degree at most 2 T Why? That’s why
![Bounded in 0 1 at integer points 1 qk 0 Large derivative 1 k Bounded in [0, 1] at integer points 1 q(k) 0 Large derivative 1 k](https://slidetodoc.com/presentation_image/32c37f864ba7ba2a6c4bffa4c964b241/image-22.jpg)
Bounded in [0, 1] at integer points 1 q(k) 0 Large derivative 1 k 2 3 . . [A. A. Markov, 1889]: Hence the original quantum algorithm must have made (N 1/5) queries N 2/5

Plan of Talk The Gospel According to Shor Three Limitations of Quantum Computers - Finding collisions in hash functions - Solving NP-complete problems with advice - Finding local optima Turning Lemons into Lemonade - Approximately learning quantum states Summary of Contributions

The Hunt for the Golden State Could there be a quantum state | left over from the Big Bang, such that given any 3 SAT instance of size 1, 000, we could quickly solve it by just measuring | in an appropriate basis? [A. , CCC 2004] In the black-box model, no: there cannot exist any “golden state” for solving NP-complete problems in polynomial time

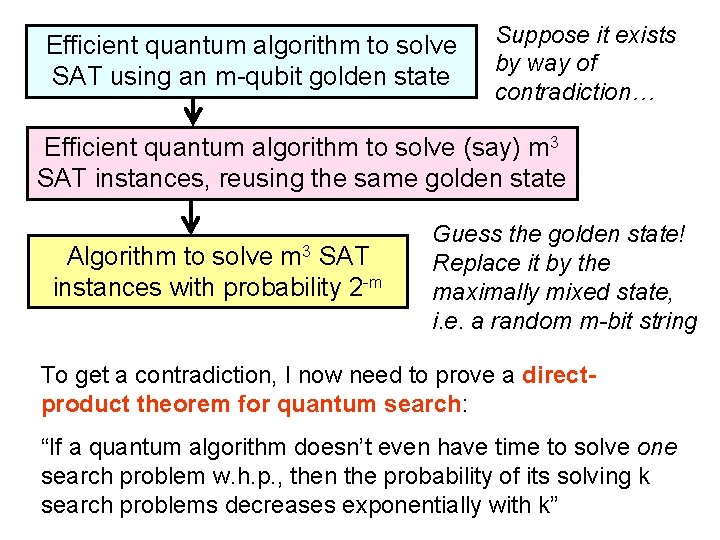
Efficient quantum algorithm to solve SAT using an m-qubit golden state Suppose it exists by way of contradiction… Efficient quantum algorithm to solve (say) m 3 SAT instances, reusing the same golden state Algorithm to solve m 3 SAT instances with probability 2 -m Guess the golden state! Replace it by the maximally mixed state, i. e. a random m-bit string To get a contradiction, I now need to prove a directproduct theorem for quantum search: “If a quantum algorithm doesn’t even have time to solve one search problem w. h. p. , then the probability of its solving k search problems decreases exponentially with k”

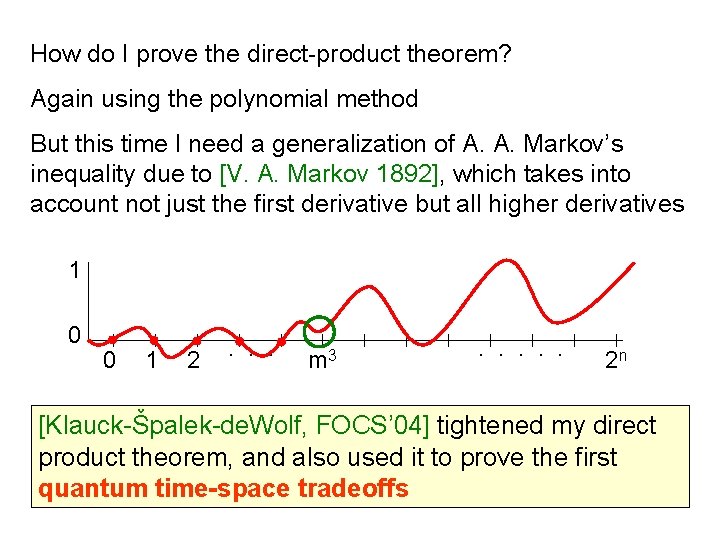
How do I prove the direct-product theorem? Again using the polynomial method But this time I need a generalization of A. A. Markov’s inequality due to [V. A. Markov 1892], which takes into account not just the first derivative but all higher derivatives 1 0 0 1 2 . . . m 3 . . . 2 n [Klauck-Špalek-de. Wolf, FOCS’ 04] tightened my direct product theorem, and also used it to prove the first quantum time-space tradeoffs

Plan of Talk The Gospel According to Shor Three Limitations of Quantum Computers - Finding collisions in hash functions - Solving NP-complete problems with advice - Finding local optima Turning Lemons into Lemonade - Approximately learning quantum states Summary of Contributions

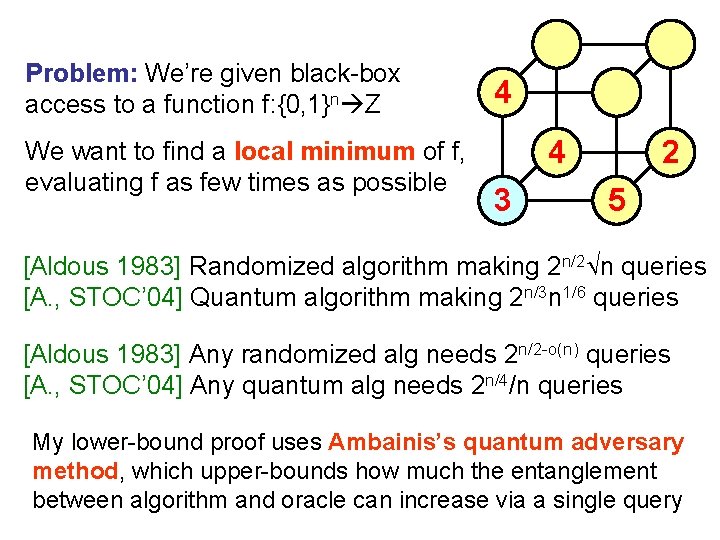
Problem: We’re given black-box access to a function f: {0, 1}n Z We want to find a local minimum of f, evaluating f as few times as possible 4 4 3 2 5 [Aldous 1983] Randomized algorithm making 2 n/2 n queries [A. , STOC’ 04] Quantum algorithm making 2 n/3 n 1/6 queries [Aldous 1983] Any randomized alg needs 2 n/2 -o(n) queries [A. , STOC’ 04] Any quantum alg needs 2 n/4/n queries My lower-bound proof uses Ambainis’s quantum adversary method, which upper-bounds how much the entanglement between algorithm and oracle can increase via a single query

Surprising part: “Quantum-inspired” argument also yields a better classical lower bound: 2 n/2/n 2 Also yields the first randomized or quantum lower bounds for local search on constant-dimensional grid graphs Quantum Generosity … Giving back because we care. TM Subsequent improvements: [Santha-Szegedy, STOC’ 04] [Zhang, STOC’ 06] [Verhoeven, 2006] [Sun-Yao, FOCS’ 06]

Plan of Talk The Gospel According to Shor Three Limitations of Quantum Computers - Finding collisions in hash functions - Solving NP-complete problems with advice - Finding local optima Turning Lemons into Lemonade - Approximately learning quantum states Summary of Contributions

The Lemon Quantum random access coding n-bit string, x 1…xn | Any one bit xi of our choice, with high probability [ANTV 1999]: | must have (n) qubits—no asymptotic savings over classical (Surprisingly, an n-qubit quantum state has no more “independently accessible degrees of freedom” than an n-bit classical string)
![The Lemonade Quantum Occams Razor Theorem A 2006 Upper bound on the sample The Lemonade “Quantum Occam’s Razor Theorem” [A. 2006] | Upper bound on the sample](https://slidetodoc.com/presentation_image/32c37f864ba7ba2a6c4bffa4c964b241/image-32.jpg)
The Lemonade “Quantum Occam’s Razor Theorem” [A. 2006] | Upper bound on the sample complexity of “PAC” (Probably Approximately Correctly) learning a quantum state Informally: Can predict approximate expectation values of most measurements on an n-qubit state, after a number of sample measurements that increases only linearly with n By contrast, traditional quantum state tomography requires ~4 n measurements Record so far: n=8 Prohibitive for much larger n

Plan of Talk The Gospel According to Shor Three Limitations of Quantum Computers - Finding collisions in hash functions - Solving NP-complete problems with advice - Finding local optima Turning Lemons into Lemonade - Approximately learning quantum states Summary of Contributions

Summary of Contributions Solved several notorious open problems about the limitations of quantum computers Gave evidence that collision-resistant hash functions can still exist in a quantum world Proved the first direct product theorem for quantum search Gave evidence against “golden states” for NP-complete problems Solved open problems about classical local optimization using quantum techniques Used a quantum coding lower bound to propose a new learning algorithm, with possible experimental implications

Ten Research Directions I Didn’t Tell You About Today Addressing skepticism Practical simulation of of quantum computing stabilizer quantum circuits with [A. , STOC 2004] Quantum computers [A. -Gottesman, Phys Rev A 2004] anthropic postselection Grover search with[A. , finite Proc. Roy. Soc. 2005] speed of light Quantum software copy[A. -Ambainis, FOCS 2003] Quantum computers with protection closed timelike curves [A. , in preparation] Provably-nonrelativizing [A. -Watrous, in preparation] circuit lower bounds Quantum versus classical proofs [A. , CCC 2006] Need to “uncompute garbage” in Complexity of Bayesian quantum algorithms [A. , QIC 2003] agreement protocols [A. -Kuperberg, CCC 2007] [A. , STOC 2005]

www. scottaaronson. com/papers
 The limits of quantum computers
The limits of quantum computers Limit involving infinity
Limit involving infinity Real limits vs. apparent limits
Real limits vs. apparent limits Quantum physics vs mechanics
Quantum physics vs mechanics Classical mechanics
Classical mechanics Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Hươu thường đẻ mỗi lứa mấy con
Hươu thường đẻ mỗi lứa mấy con Diễn thế sinh thái là
Diễn thế sinh thái là Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Phép trừ bù
Phép trừ bù Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Lời thề hippocrates
Lời thề hippocrates đại từ thay thế
đại từ thay thế Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Công thức tính độ biến thiên đông lượng
Công thức tính độ biến thiên đông lượng Môn thể thao bắt đầu bằng chữ f
Môn thể thao bắt đầu bằng chữ f Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Khi nào hổ mẹ dạy hổ con săn mồi
Khi nào hổ mẹ dạy hổ con săn mồi Các loại đột biến cấu trúc nhiễm sắc thể
Các loại đột biến cấu trúc nhiễm sắc thể Nguyên nhân của sự mỏi cơ sinh 8
Nguyên nhân của sự mỏi cơ sinh 8 Phản ứng thế ankan
Phản ứng thế ankan Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan điện thế nghỉ
điện thế nghỉ Một số thể thơ truyền thống
Một số thể thơ truyền thống Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Sơ đồ cơ thể người
Sơ đồ cơ thể người So nguyen to
So nguyen to Fecboak
Fecboak đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Chụp phim tư thế worms-breton
Chụp phim tư thế worms-breton ưu thế lai là gì
ưu thế lai là gì