6 2 What is Probability Three different approaches

6. 2 What is Probability? Three different approaches to probability

1. The Classical Approach When the outcomes in a sample space are equally likely, the probability of an event E, denoted by P(E), is the ratio of the number of outcomes favorable to E to the total number of outcomes in the sample space. Examples: flipping a coin, rolling a die, etc.

2. The Subjective Approach Probability can be interpreted as a personal measure of the strength of belief that a particular outcome will occur. Example: You think you have an 95% chance of your parents calls today to ask how is your day The classical approach doesn’t work for every situation.

The Subjective Approach? The problem with a subjective approach is that different people could assign different probabilities to the same outcome based on their subjective viewpoints.

Examples: “In the subjective approach we define probability as the degree of belief that we hold in the occurrence of an event” • P(you are taking the AP-Stats official exam in May) • P(Your October SAT score goes up)

• P(CNSA successfully land a man on the moon) (I think CNSA is Chinese’s NASA. Am I right? • P(girlfriend says yes when you ask her to marry you)

3. The Relative Frequency Approach/Empirical Approach

What if you consider the probability of a penalty shootout? By inexperienced and experienced player?

3. The Relative Frequency Approach/Empirical Approach Probabilities are assigned on the basis of experimentation or historical data.

The probability of event E, denoted by P(E), is defined to be the value approached by the relative frequency of occurrence of E in a very long series of trials of a chance experiment. Thus, if the number of trials is quite large,

Probability gives us a language to describe the long-term regularity of random behavior.

Law of Large Numbers (LLN) Let’s do an activity to understand what LLN mean?

Plenary: Summary on Methods for Determining Probability 1. The classical approach: Appropriate for experiments that can be described with equally likely outcomes. 2. The subjective approach: Probabilities represent an individual’s judgment based on facts combined with personal evaluation of other information. 3. The relative frequency/empirical approach: An estimate is based on an accumulation of experimental results or historical data. This estimate, usually derived empirically, presumes a replicable chance experiment.

Classwork Which definitions do you think could be used for obtaining the following probabilities? i) A person’s birthday is on November 4 th ii) You have a claim on your car insurance in next year iii) There is a Chinese economic recession during the next 5 years

Law of Large Numbers (LLN) As the number of repetitions of a chance experiment increase, the chance that the relative frequency of occurrence for an event will differ from the true probability by more than any small number approaches 0. OR in other words, after a large number of trials, the relative frequency approaches the true probability.

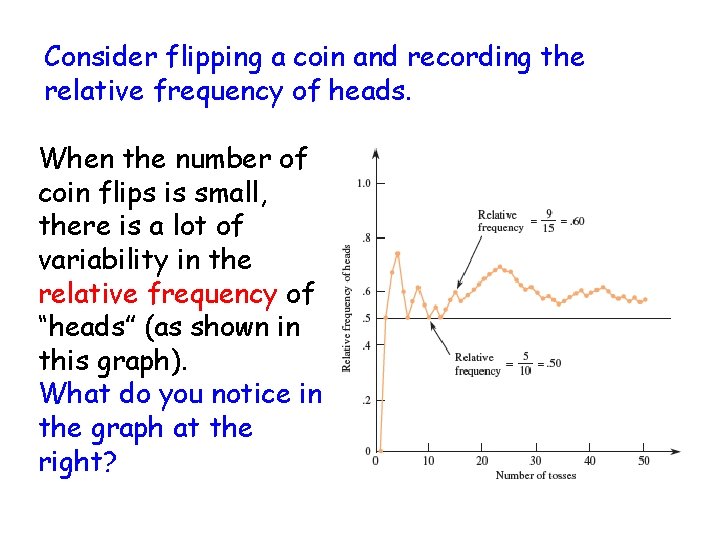
Consider flipping a coin and recording the relative frequency of heads. When the number of coin flips is small, there is a lot of variability in the relative frequency of “heads” (as shown in this graph). What do you notice in the graph at the right?

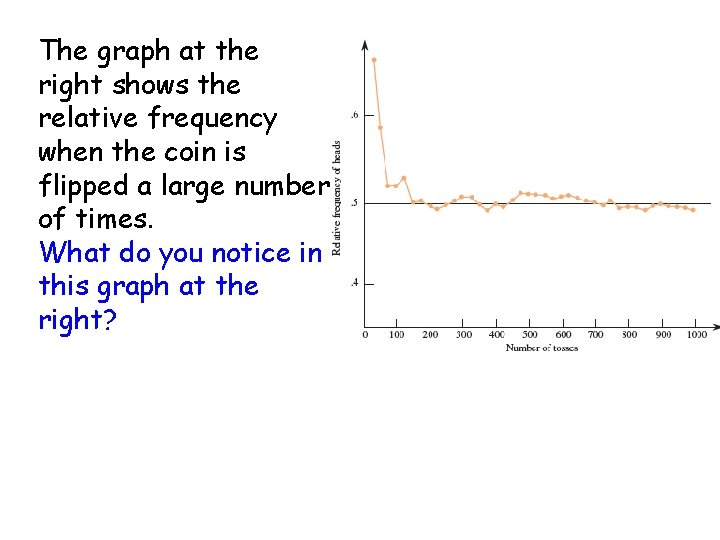
The graph at the right shows the relative frequency when the coin is flipped a large number of times. What do you notice in this graph at the right?

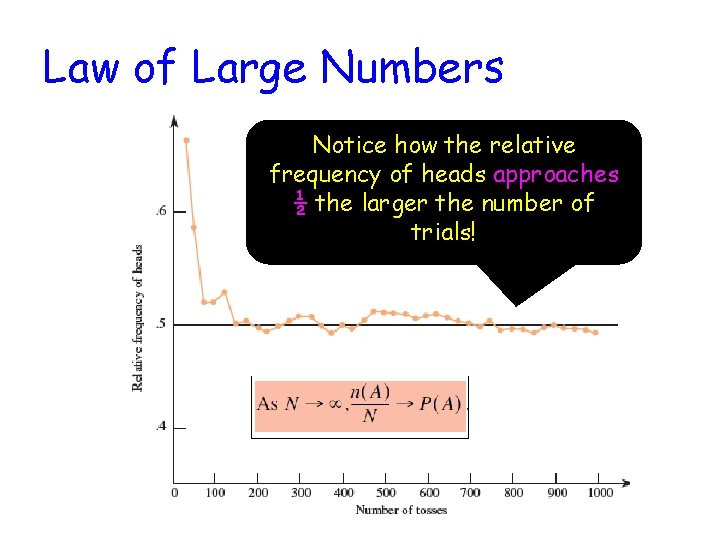
Law of Large Numbers Notice how the relative frequency of heads approaches ½ the larger the number of trials!

Activity to demonstrate LLN (Law of large Numbers) Follow the following steps: • This should be done in groups, 4 students in a group. • Each group will get 5 coins. • Flip the coins 20 times. (Flipping the 5 coins is considered as a one trial/toss) • Each time count the number of heads (lotus flower on 1 RMB) and record the cumulative number of heads. (Cumulative number of heads is the total number of heads in all the previous trials. ) • Calculate the cumulative mean after each new trial. *(feel free to ask me if you are not sure of this step) • Then put the cumulative means into a time series graph. • When you finish with the graph, show me your work and draw the graph on the white board. • Conclusion: ? ? ?

Record Sheet Trial Number #of heads 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Cumulative # of heads Proportion of cumulative heads (Relative frequency of heads)