Quantum decoherence entanglement and thermodynamics Gershon Kurizki Weizmann



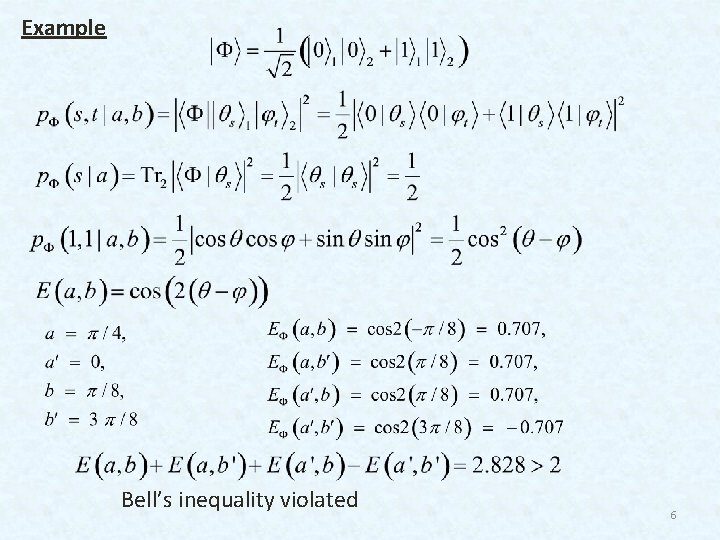












- Slides: 25

Quantum decoherence, entanglement and thermodynamics Gershon Kurizki Weizmann Institute of Science Crete-Lecture 2016 1

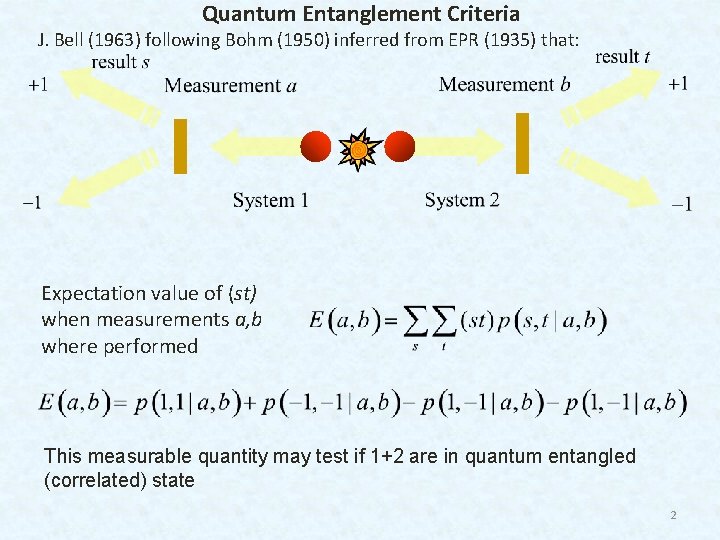
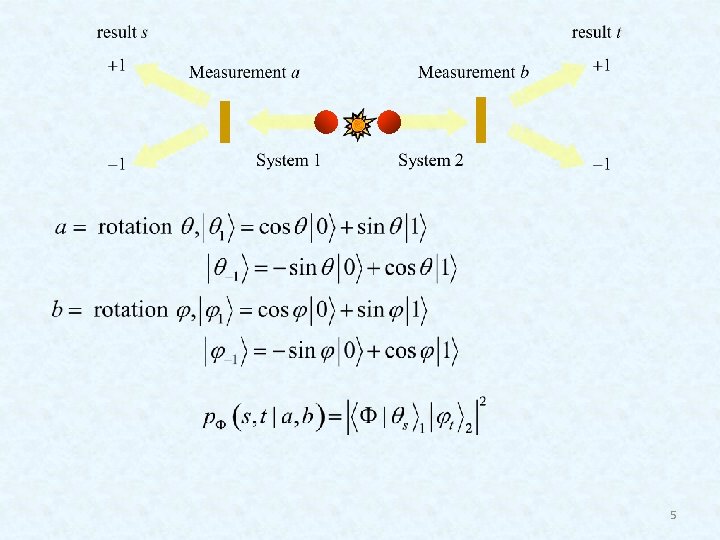
Quantum Entanglement Criteria J. Bell (1963) following Bohm (1950) inferred from EPR (1935) that: Expectation value of (st) when measurements a, b where performed This measurable quantity may test if 1+2 are in quantum entangled (correlated) state 2

CHSH inequality (1969) John Clauser, Michael Horne, Abner Shimony and Richard Holt Counting probabilities from four different experiments: a, b a’, b a, b’ a’, b’ Any experiment that violates these inequalities, proves non-classicality and non-locality (but non-causality!) 3

CHSH inequality (1969) Locality Remote outcome independence Remote context independence 4

5
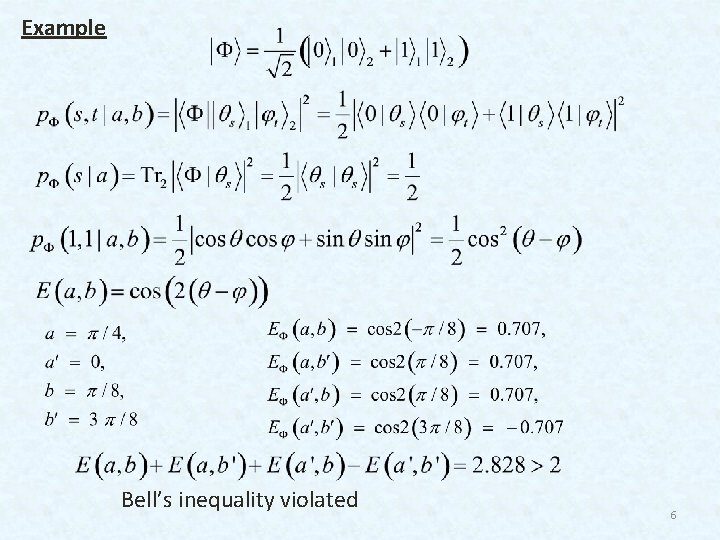
Example Bell’s inequality violated 6

Bell (CHSH) inequalities Violation of CHSH inequalities imply a non-local theory and precludes local (hidden-variable) models. This means that measuring one system changes the probabilities of the other system’s measurement. 7

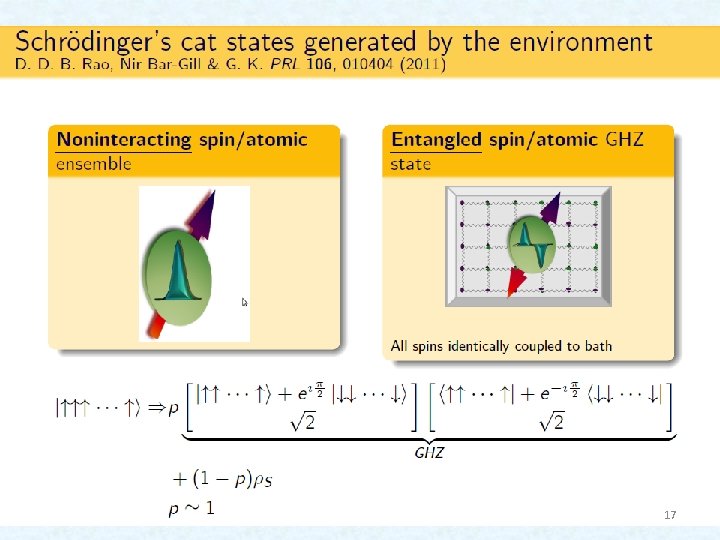
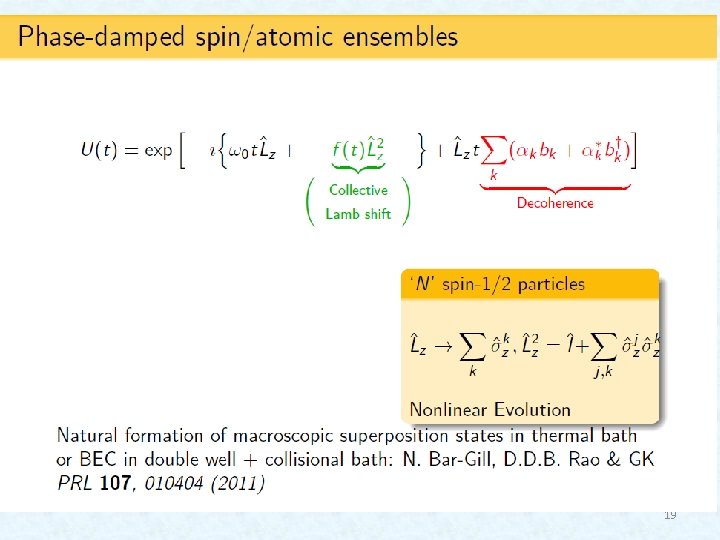
Entanglement of atom, meter and environment Why is entanglement not encountered in daily life? Because of the environment (Zurek). 8

System in coherent state - Initial cat state of the system Schroedinger (1935): Cat is entangled with radioactive atom 9

10

Pointer Basis Environment System Meter Phase 1: Phase 2: Back-action evasion condition Invariant 11

Dynamical model for a quantum measurement Phase 1: (no environment) Two coupled oscillator modes coherent state Approximately orthogonal 12

Dynamical model for a quantum measurement Phase 2: (environment action on M) Coupling to collection of modes For Non-Markovian For Markovian 13

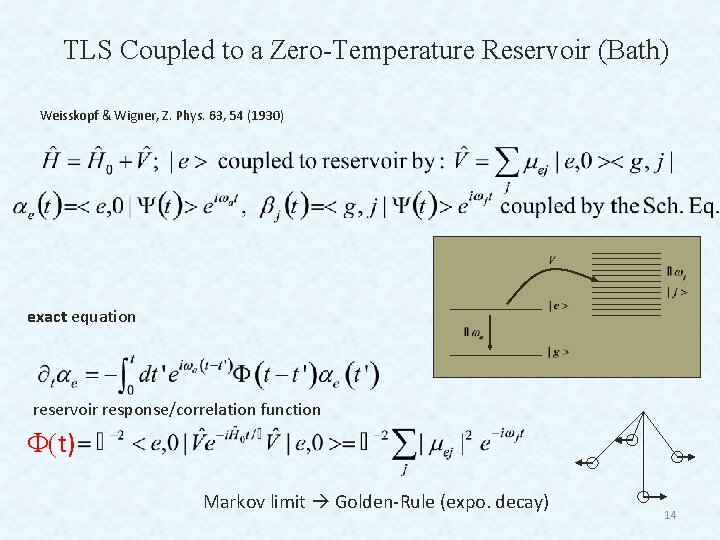
TLS Coupled to a Zero-Temperature Reservoir (Bath) Weisskopf & Wigner, Z. Phys. 63, 54 (1930) exact equation reservoir response/correlation function (t) Markov limit Golden-Rule (expo. decay) 14

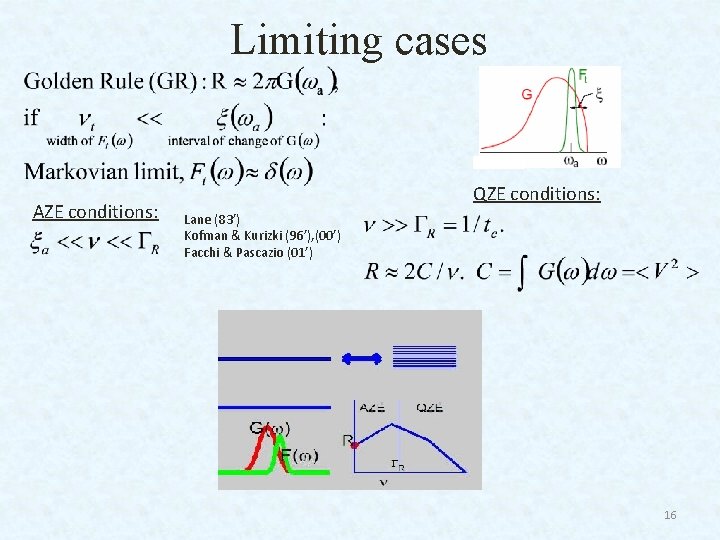
Universal Formula A. G. Kofman and G. Kurizki, Nature 405, 546 (2000), PRL 87, 270405 (2001), PRL 93, 130406(2004) Measurements / phase modulation / perturbation: V(t)= (t)Vs Exact (reversible) evolution: e(t) decays slower than (t) ) e(t’) e(t) Coherent or random (t) yields universal modified decay rate: Overlap of reservoir coupling spectrum and the spectral intensity of modulation Ft( )=| t( )|2 short t Ã! broad 15

Limiting cases AZE conditions: QZE conditions: Lane (83’) Kofman & Kurizki (96’), (00’) Facchi & Pascazio (01’) 16

17

18

19

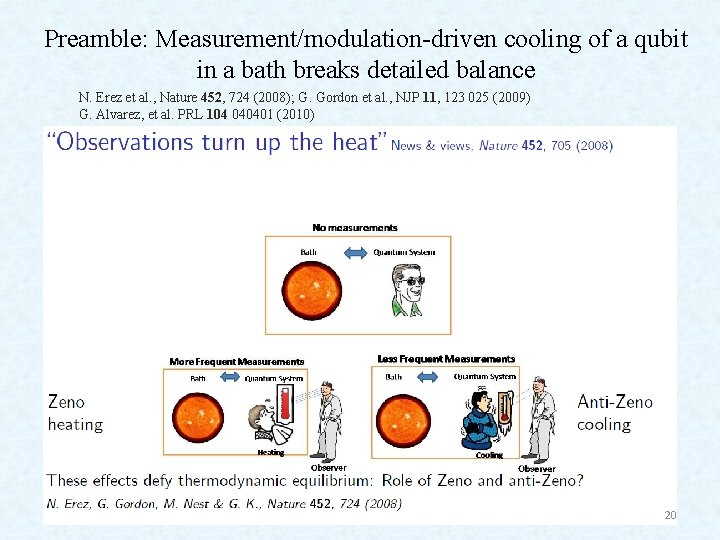
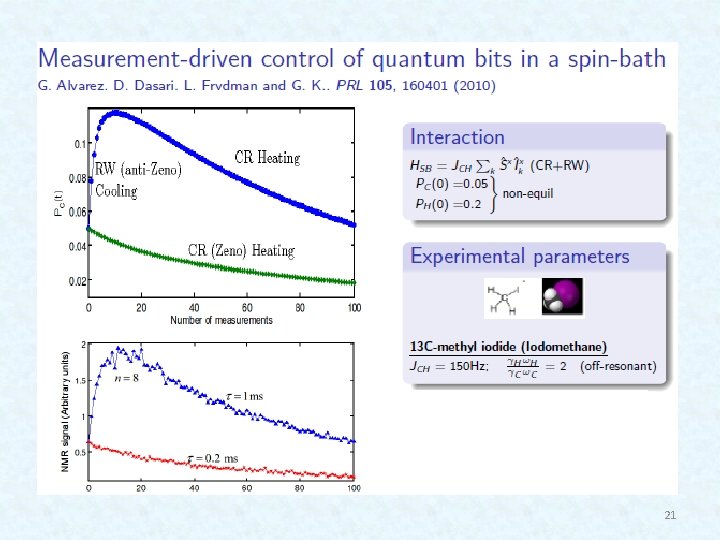
Preamble: Measurement/modulation-driven cooling of a qubit in a bath breaks detailed balance N. Erez et al. , Nature 452, 724 (2008); G. Gordon et al. , NJP 11, 123 025 (2009) G. Alvarez, et al. PRL 104 040401 (2010) 20

21

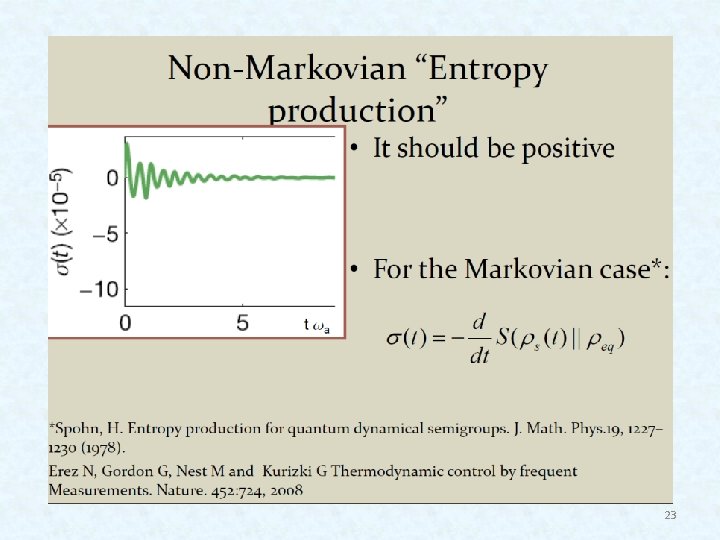
22

23

Conclusions Ø Entanglement criteria: Bell’s inequality violation Ø Macroscopic entanglement destroyed by environment (bath? ) Ø Only if Markovian relaxation of system bath is assumed towards pointer states Ø If system is probed on non-Markovian time scales and relaxation changes: Zeno/anti-Zeno Ø Bath can entangle systems Ø Measurement thermodynamics: Zeno can heat, anti-Zeno can cool 24

25