Topic 5 Schrdinger Equation Wave equation for Photon

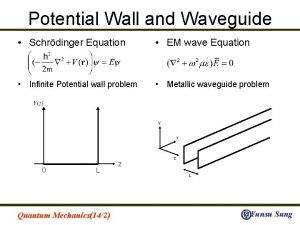
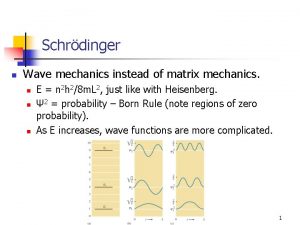
Topic 5: Schrödinger Equation • Wave equation for Photon vs. Schrödinger equation for Electron+ • Solution to Schrödinger Equation gives wave function – 2 gives probability of finding particle in a certain region • Square Well Potentials: Infinite and Finite walls – oscillates inside well and is zero or decaying outside well, E n 2 • Simple Harmonic Oscillator Potential (or parabolic) – is more complex, E n Example Infinite Well Solution Page 1

Schrödinger Equation • Step Potential of Height V 0 – is always affected by a step, even if E > V 0 – For E > V 0, oscillates with different k values outside/inside step. – For E < V 0, oscillates outside step and decays inside step. • Barrier Potential of Height V 0 – oscillates outside and decays inside barrier. • Expectation Values and Operators • Appendix: Complex Number Tutorial Page 2

Wave Equation for Photons: Electric Field E 2 nd space derivative 2 nd time derivative Propose Solution: Calculate Derivatives: After Substitution: Page 3

Schrödinger Eqn. for Electrons+: Wave Function 2 nd space derivative 1 st time derivative Propose Simple Solution for constant V: Calculate Derivatives: After Substitution: Page 4

Schrödinger Equation: Applications • Now, find the eigenfunctions and eigenvalues E of the Schrödinger Equation for a particle interacting with different potential energy shapes. (assume no time dependence) • Possible potential energies V(x) include: • Infinite and Finite square wells (bound particle). • Simple Harmonic or parabolic well (bound particle). • Step edge (free particle). • Barrier (free particle). Page 5

Schrödinger Equation: Definitions • Wave function has NO PHYSICAL MEANING! • BUT, the probability to find a particle in width dx is given by: • Normalization of – Probability to find particle in all space must equal 1. – Solve for coefficients so that normalization occurs. Page 6

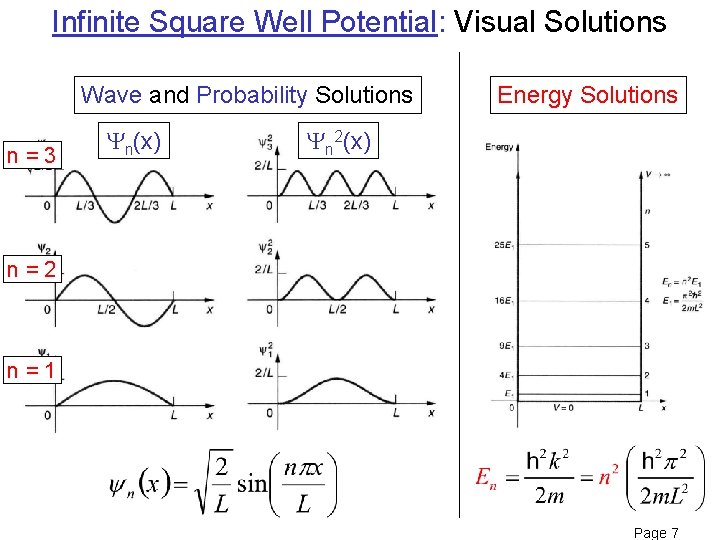
Infinite Square Well Potential: Visual Solutions Wave and Probability Solutions n=3 n(x) Energy Solutions n 2(x) n=2 n=1 Page 7

Infinite Square Well: Solve general from S. Eqn. Inside Well: (V = 0) where Oscillatory Outside Well: (V = ) cannot penetrate barriers! Page 8

Infinite Square Well: Satisfy B. C. and Normalization • Satisfy boundary conditions Quantized Energy Solutions • Satisfy normalization using identity and Wave Solutions Page 9

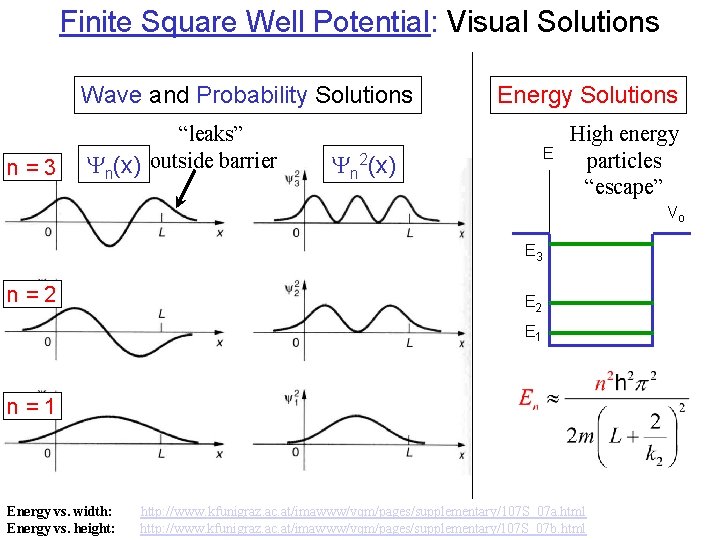
Finite Square Well Potential: Visual Solutions Wave and Probability Solutions n=3 “leaks” n(x) outside barrier n Energy Solutions E 2(x) High energy particles “escape” Vo E 3 n=2 E 1 n=1 Energy vs. width: Energy vs. height: http: //www. kfunigraz. ac. at/imawww/vqm/pages/supplementary/107 S_07 a. html http: //www. kfunigraz. ac. at/imawww/vqm/pages/supplementary/107 S_07 b. html Page 10

Finite Square Well: Solve general from S. Eqn. Inside Well: (V = 0) where Oscillatory Outside Well: (V = Vo) Decaying where can penetrate barriers! Page 11

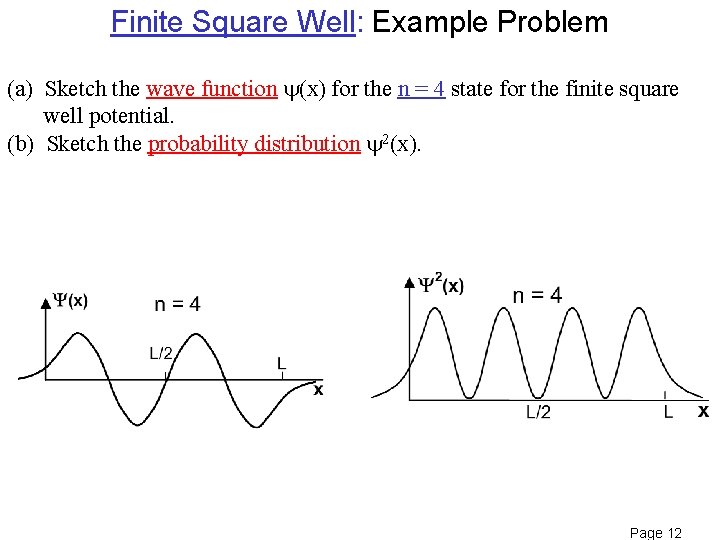
Finite Square Well: Example Problem (a) Sketch the wave function (x) for the n = 4 state for the finite square well potential. (b) Sketch the probability distribution 2(x). Page 12

Finite Square Well: Example Problem Sketch the wave function (x) corresponding to a particle with energy E in the potential well shown below. Explain how and why the wavelengths and amplitudes of (x) are different in regions 1 and 2. • (x) oscillates inside the potential well because E > V(x), and decays exponentially outside the well because E < V(x). • The frequency of (x) is higher in Region 1 vs. Region 2 because the kinetic energy is higher [Ek = E - V(x)]. • The amplitude of (x) is lower in Region 1 because its higher Ek gives a higher velocity, and the particle therefore spends less time in that region. Page 13

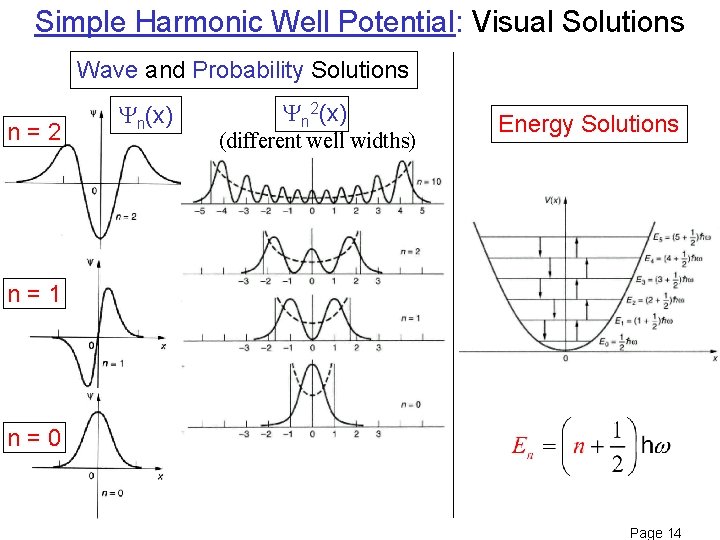
Simple Harmonic Well Potential: Visual Solutions Wave and Probability Solutions n=2 n(x) n 2(x) (different well widths) Energy Solutions n=1 n=0 Page 14

Simple Harmonic Well: Solve from S. Eqn. NEW! Inside Well: where (x) is not a simple trigonometric function. Outside Well: where (x) is not a simple decaying exponential. Page 15

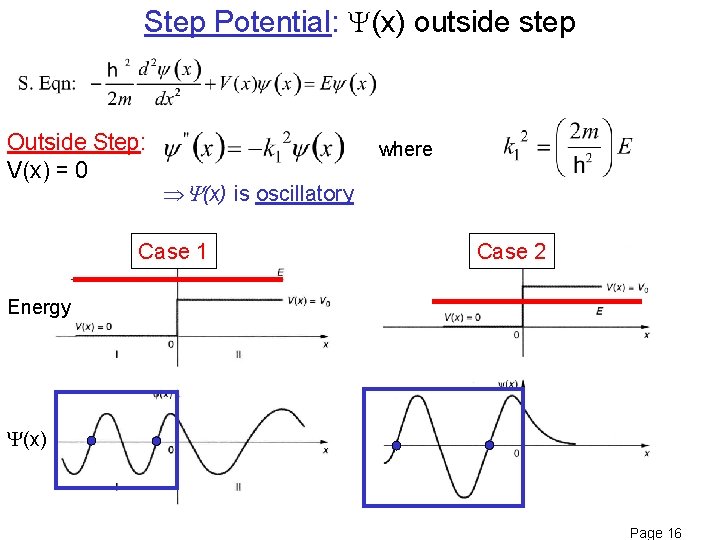
Step Potential: (x) outside step Outside Step: V(x) = 0 where Y(x) is oscillatory Case 1 Case 2 Energy (x) Page 16

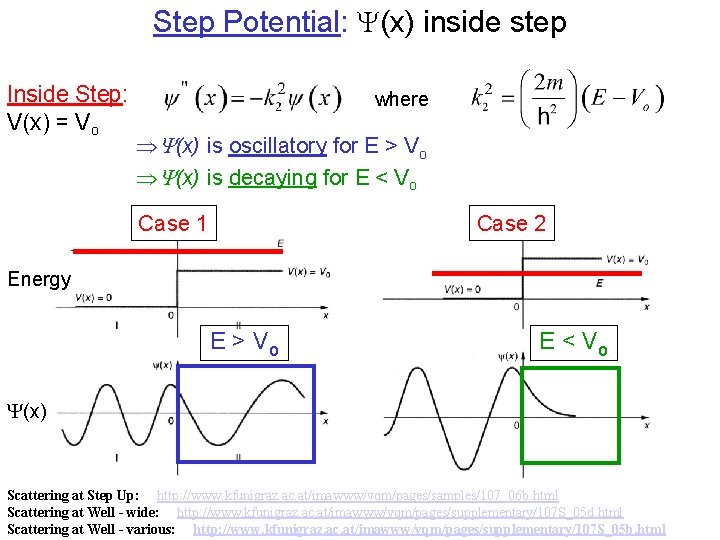
Step Potential: (x) inside step Inside Step: V(x) = Vo where Y(x) is oscillatory for E > Vo Y(x) is decaying for E < Vo Case 1 Case 2 Energy E > Vo E < Vo (x) Scattering at Step Up: http: //www. kfunigraz. ac. at/imawww/vqm/pages/samples/107_06 b. html Scattering at Well - wide: http: //www. kfunigraz. ac. at/imawww/vqm/pages/supplementary/107 S_05 d. html Scattering at Well - various: http: //www. kfunigraz. ac. at/imawww/vqm/pages/supplementary/107 S_05 b. html Page 17

Step Potential: Reflection and Transmission • At a step, a particle wave undergoes reflection and transmission (like electromagnetic radiation!) with probability rates R and T, respectively. R(reflection) + T(transmission) = 1 • Reflection occurs at a barrier (R 0), regardless if it is step-down or step-up. – R depends on the wave vector difference (k 1 - k 2) (or energy difference), but not on which is larger. – Classically, R = 0 for energy E larger than potential barrier (Vo). Page 18

Step Potential: Example Problem A free particle of mass m, wave number k 1 , and energy E = 2 Vo is traveling to the right. At x = 0, the potential jumps from zero to –Vo and remains at this value for positive x. Find the wavenumber k 2 in the region x > 0 in terms of k 1 and Vo. In addition, find the reflection and transmission coefficients R and T. Page 19

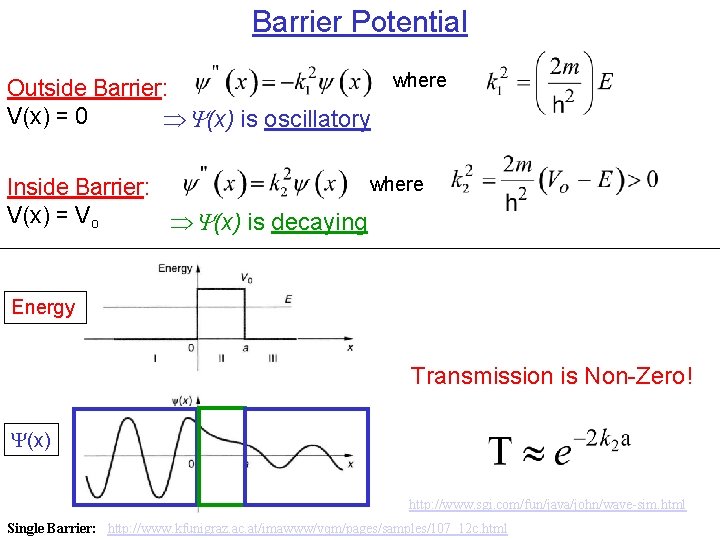
Barrier Potential where Outside Barrier: V(x) = 0 Y(x) is oscillatory where Inside Barrier: V(x) = Vo Y(x) is decaying Energy Transmission is Non-Zero! (x) http: //www. sgi. com/fun/java/john/wave-sim. html Single Barrier: http: //www. kfunigraz. ac. at/imawww/vqm/pages/samples/107_12 c. html Page 20

Barrier Potential: Example Problem Sketch the wave function (x) corresponding to a particle with energy E in the potential shown below. Explain how and why the wavelengths and amplitudes of (x) are different in regions 1 and 3. • (x) oscillates in regions 1 and 3 because E > V(x), and decays exponentially in region 2 because E < V(x). • Frequency of (x) is higher in Region 1 vs. 3 because kinetic energy is higher there. • Amplitude of (x) in Regions 1 and 3 depends on the initial location of the wave packet. If we assume a bound particle in Region 1, then the amplitude is higher there and decays into Region 3 (case shown above). Non-resonant Barrier: http: //www. kfunigraz. ac. at/imawww/vqm/pages/supplementary/107 S_resonance-5. html Resonant Barrier: http: //www. kfunigraz. ac. at/imawww/vqm/pages/supplementary/107 S_resonance-6. html Double Barrier + : http: //www. kfunigraz. ac. at/imawww/vqm/pages/supplementary/107 S_resonance-0. html Page 21

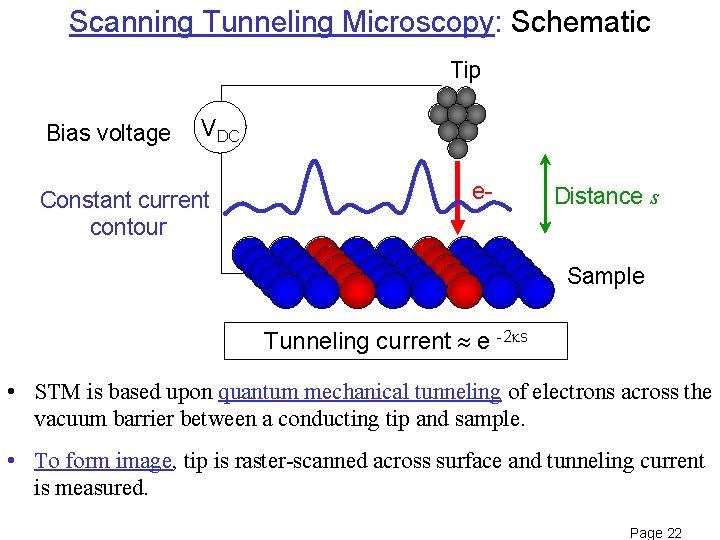
Scanning Tunneling Microscopy: Schematic Tip Bias voltage VDC e- Constant current contour e e Distance s Sample Tunneling current e -2 ks • STM is based upon quantum mechanical tunneling of electrons across the vacuum barrier between a conducting tip and sample. • To form image, tip is raster-scanned across surface and tunneling current is measured. Page 22

STM: Ultra-High Vacuum Instrument Coarse Motion Sample Scanner Tip • Well-ordered, clean surfaces for STM studies are prepared in UHV. • Sample is moved towards tip using coarse mechanism, and the tip is moved using a 3 -axis piezoelectric scanner. Page 23

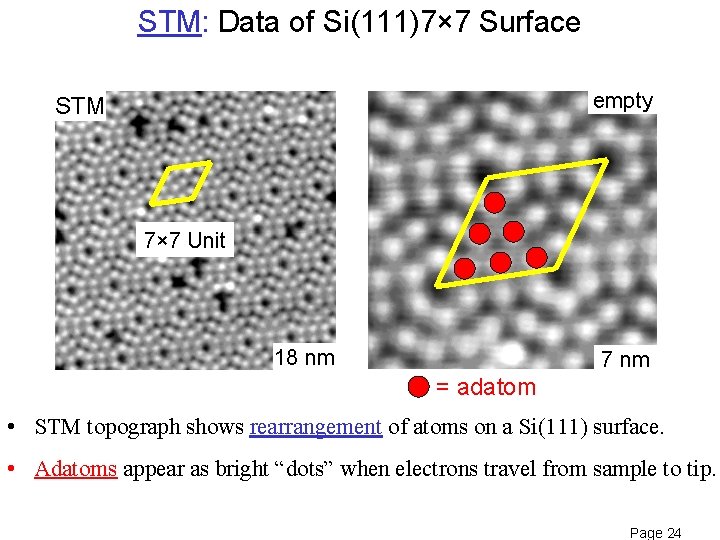
STM: Data of Si(111)7× 7 Surface empty STM 7× 7 Unit 18 nm 7 nm = adatom • STM topograph shows rearrangement of atoms on a Si(111) surface. • Adatoms appear as bright “dots” when electrons travel from sample to tip. Page 24

Expectation Values and Operators • By definition, the “expectation value” of a function is: • “Operate” on (x) to find expectation value (or average expected value) of an “observable. ” Observable Symbol Momentum p Position x Operator x Kinetic energy K Hamiltonian H Total Energy E Page 25

Expectation Values: Example Problem • Find <p>, <p 2> for ground state 1(x) of infinite well (n = 1) L 0 <p> = -L/2 +L/2 <p> = 0 by symmetry (odd function over symmetric limits) Note: The average momentum goes to zero because the “sum” of positive and negative momentum values cancel each other out. Page 26

Expectation Values: Example Problem, cont. <p 2> = = 1 by normalization <p 2> = Page 27

Complex Number Tutorial: Definitions • Imaginary number i given by: i 2 = – 1 ( i 3 = –i, i 4 = 1, i– 1 = –i ) • Complex number z is composed of a real and imaginary parts. Cartesian Form: z = x + iy Polar Form: z = r(cosq + i sinq) where r = (x 2 + y 2)1/2 and tanq = y/x Exponential Form: z = rei q Conjugate: z* = x – iy = rcosq – i rsinq = re– i q where (z*)(z) = (x – iy)(x + iy) = x 2 + y 2 (real!) Page 28

Complex Number Tutorial: Taylor Series • Proof of equivalence for polar and exponential forms: Page 29

Schrödinger Eqn. : Derivation of Space & Time Dependence Schrödinger Equation is 2 nd Order Partial Differential Equation Assume is separable [i. e. V(x) only] Substitution of Partial derivatives are now ordinary derivatives Divide by (x)0(t) Space dependence ONLY Time dependence ONLY Page 30

Schrödinger Eqn. : Derivation of Space & Time Dependence Left and right sides have only space (x) and time (t) dependence now Space: Set each side of equation equal to a constant C Time: Space Equation need V(x) to solve! Time Solution: Check by substitution! Page 31