Decoherence and all that Artur Ekert Quantum vs

Decoherence and all that Artur Ekert

Quantum vs classical Interference term

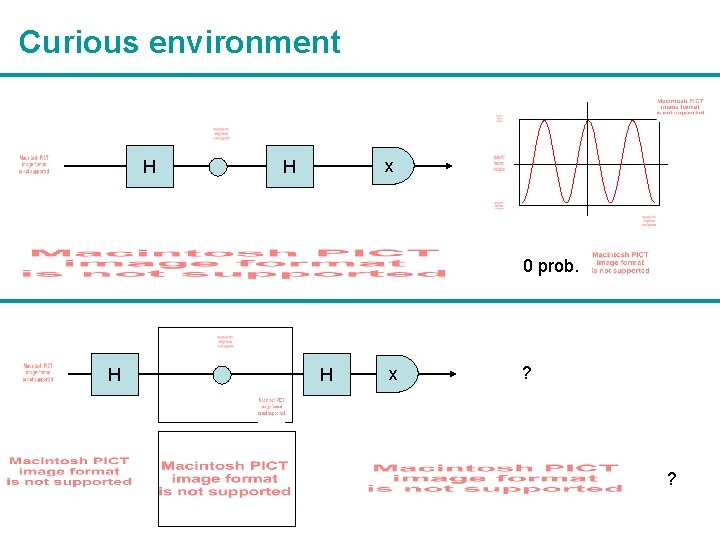
Curious environment H x H 0 prob. H H x ? ?

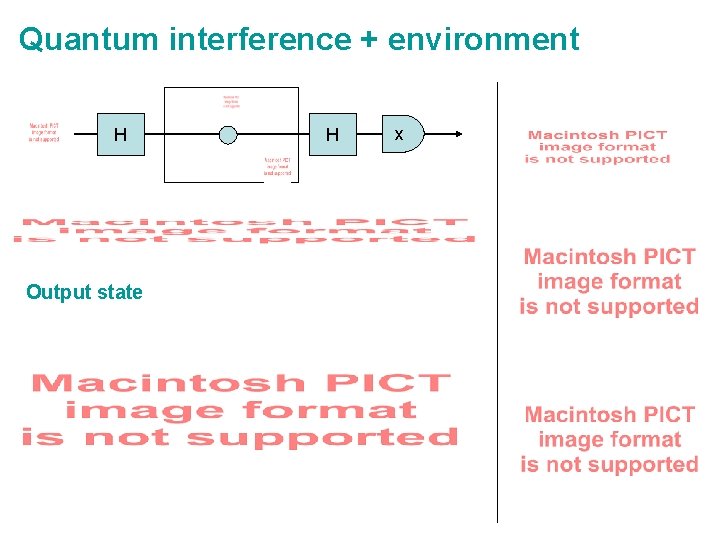
Quantum interference + environment H Output state H x

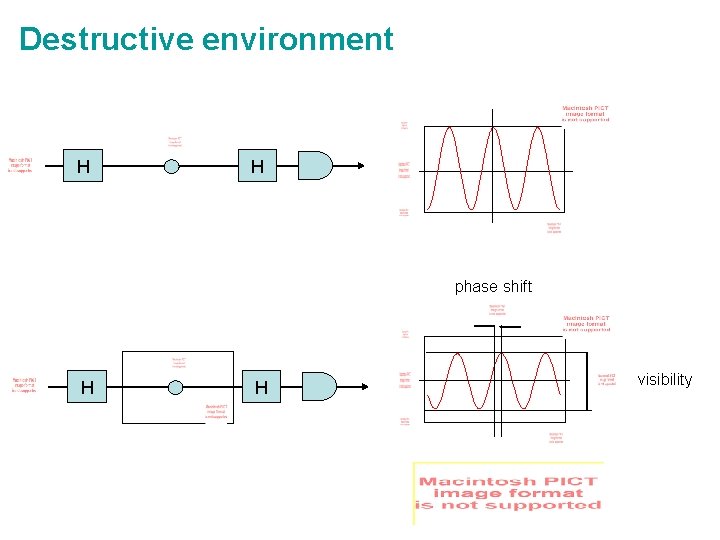
Destructive environment H H phase shift H H visibility

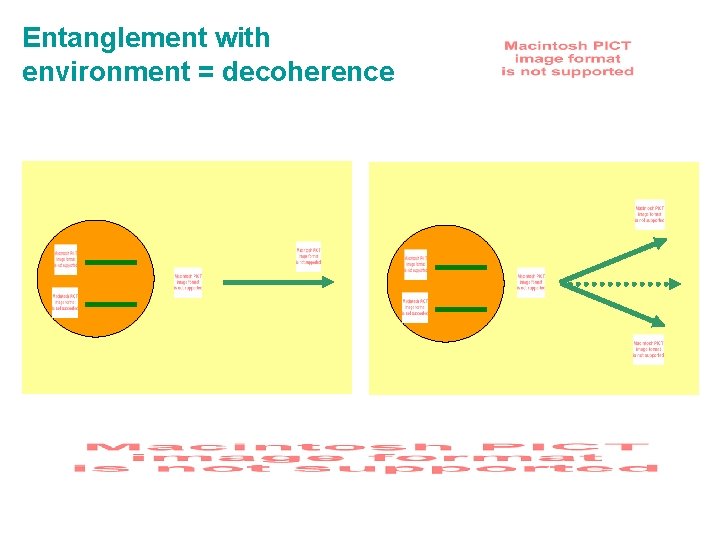
Entanglement with environment = decoherence

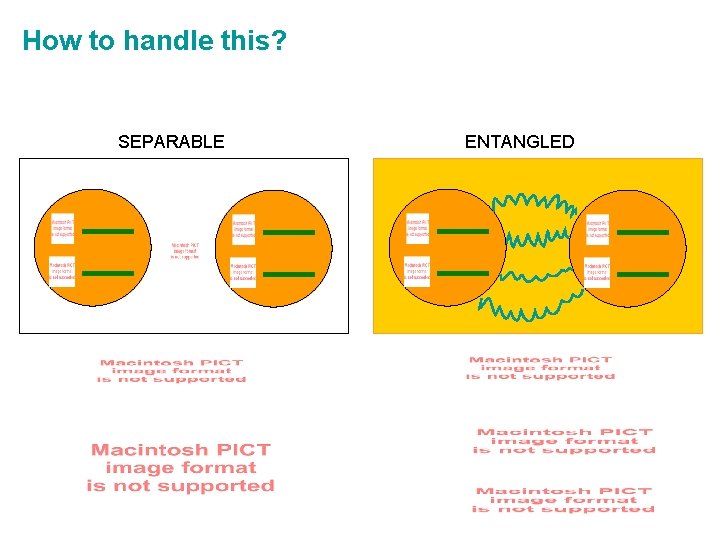
How to handle this? SEPARABLE ENTANGLED

How to describe a quantum state of an entangled subsystem? An alternative way of representing quantum states is in terms of density matrices (a. k. a. density operators)

Density matrices

Density matrices The density matrix of a pure state ψ is the matrix = ψ ψ coherences populations

Density matrices The density matrix of a pure state ψ is the matrix = ψ ψ For a qubit:

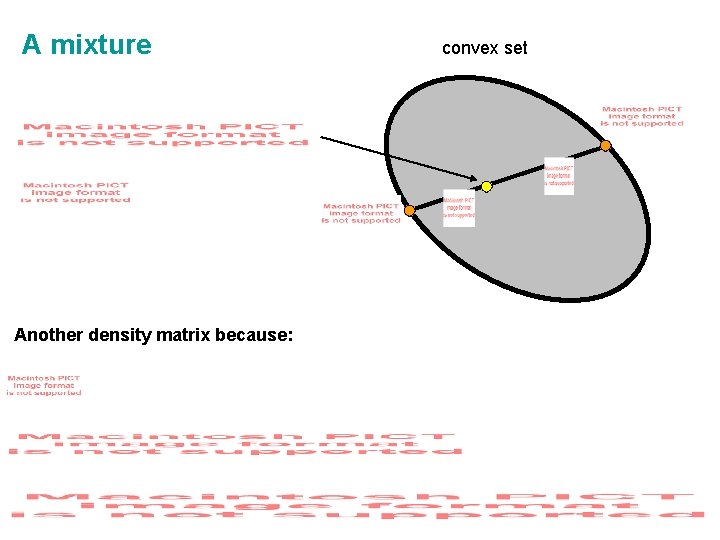
A mixture Another density matrix because: convex set

Density matrices – evolution and measurement Unitary evolution Measurement - resolution of the identity outcome k with probability

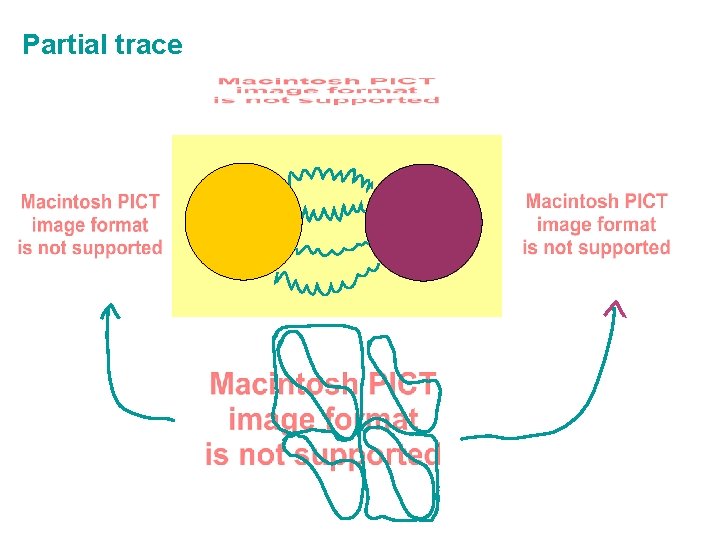
Partial trace

Partial trace Trace Partial trace

Partial trace over B

Partial trace over B

Partial trace over B

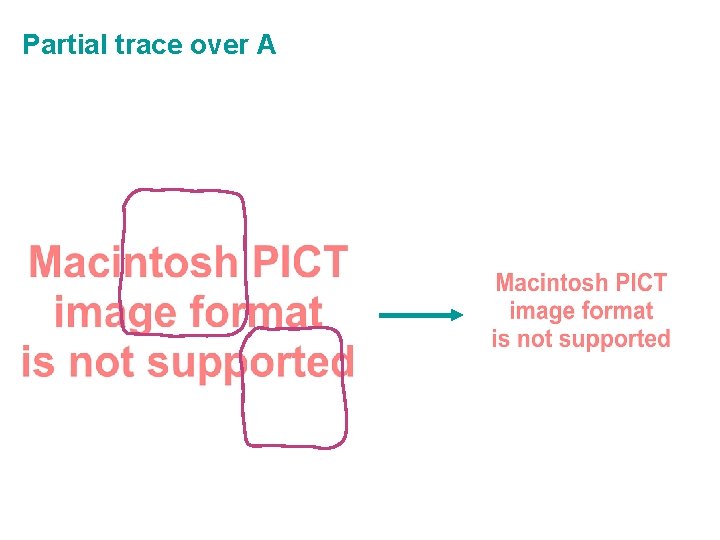
Partial trace over A

Partial trace over A

Partial trace

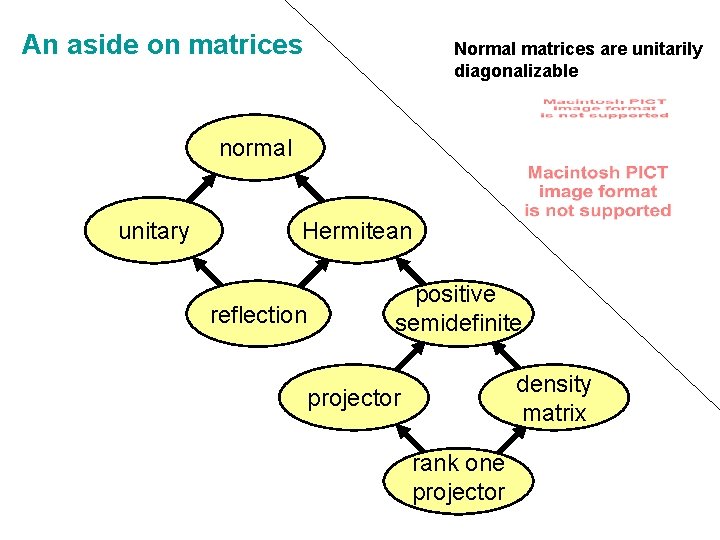
An aside on matrices Normal matrices are unitarily diagonalizable normal unitary Hermitean reflection positive semidefinite density matrix projector rank one projector

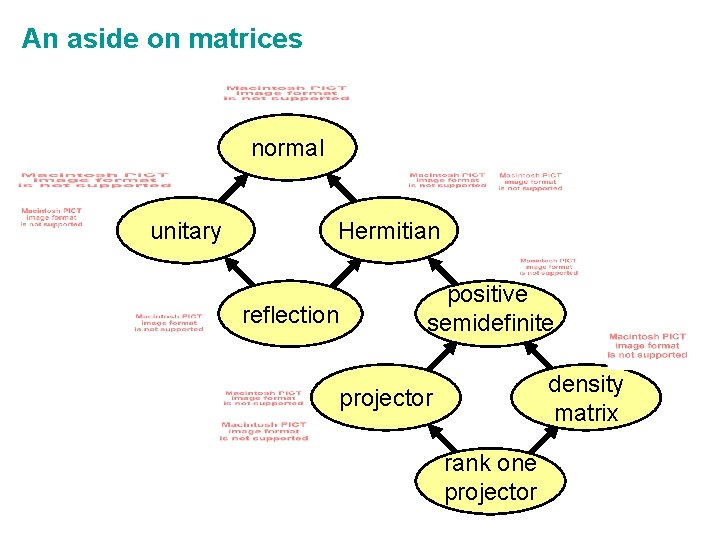
An aside on matrices normal unitary Hermitian reflection positive semidefinite density matrix projector rank one projector

An aside on matrices ABNORMAL MATRICES NOT DIAGONALIZABLE BUT NOT UNITARILY eigenvectors

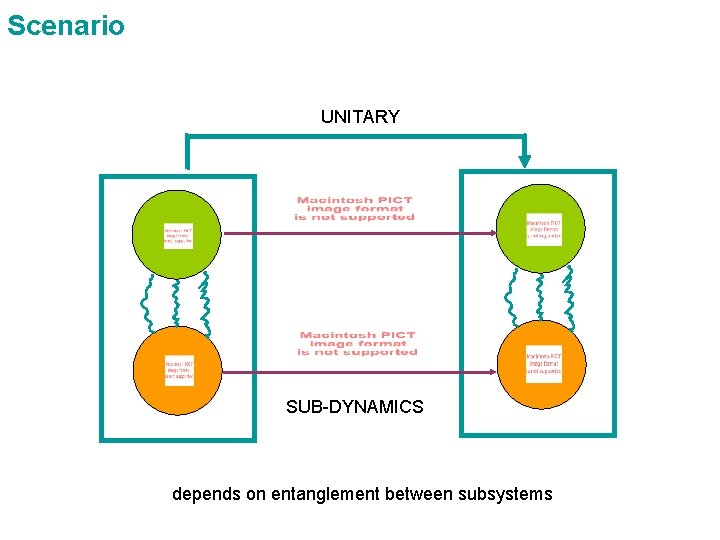
Scenario UNITARY SUB-DYNAMICS depends on entanglement between subsystems

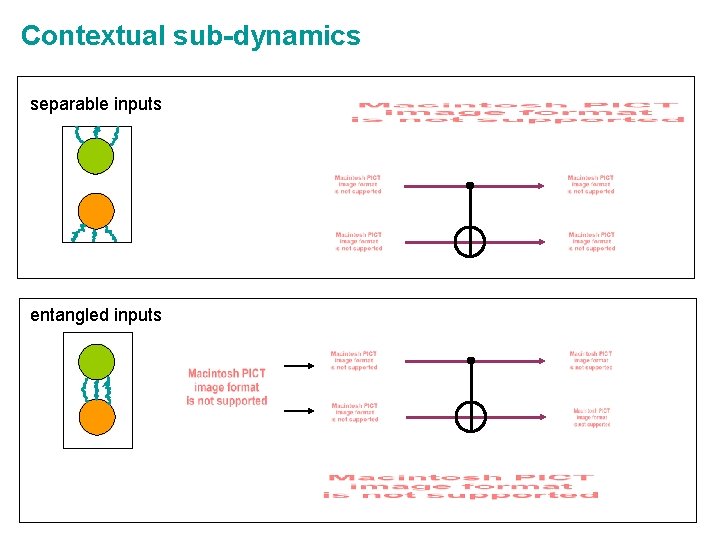
Contextual sub-dynamics separable inputs entangled inputs

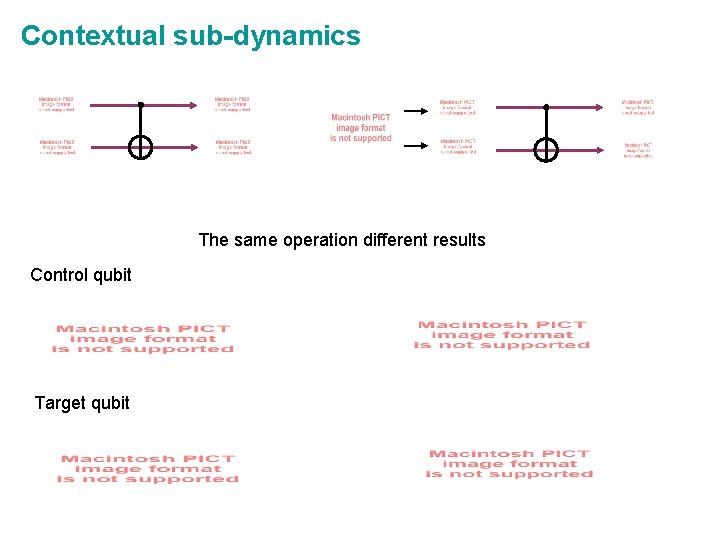
Contextual sub-dynamics The same operation different results Control qubit Target qubit

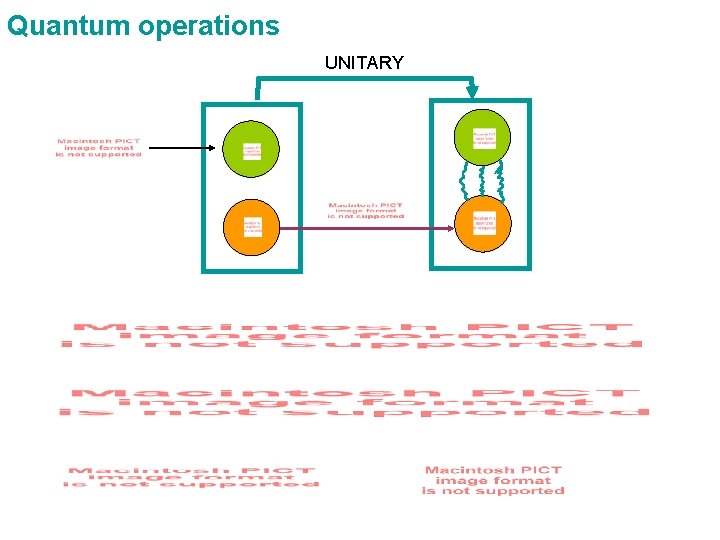
Quantum operations UNITARY

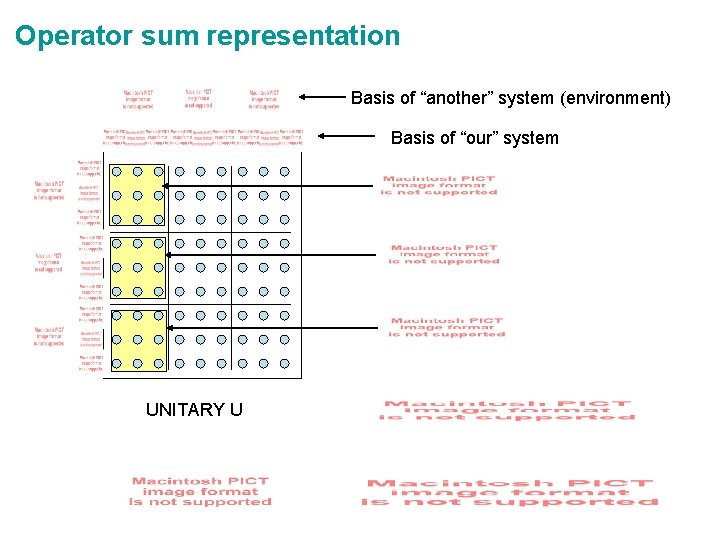
Operator sum representation Basis of “another” system (environment) Basis of “our” system UNITARY U

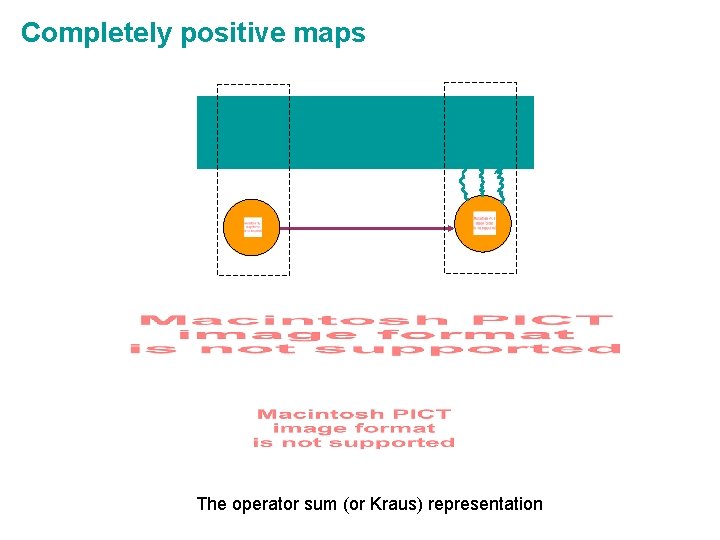
Completely positive maps The operator sum (or Kraus) representation

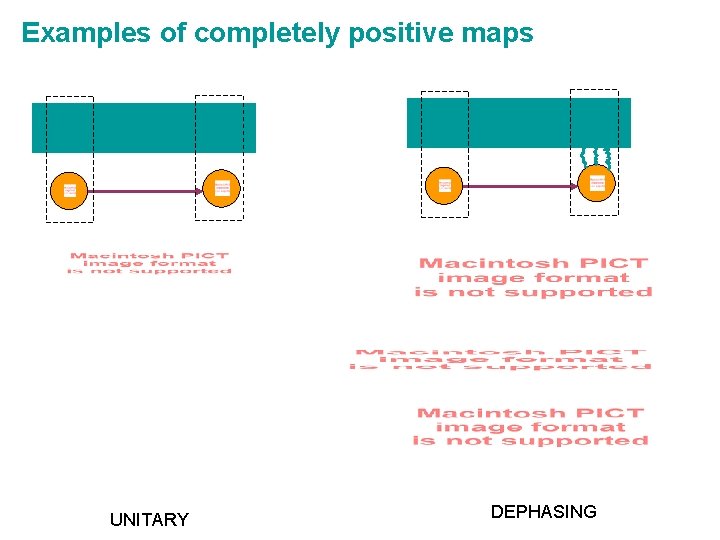
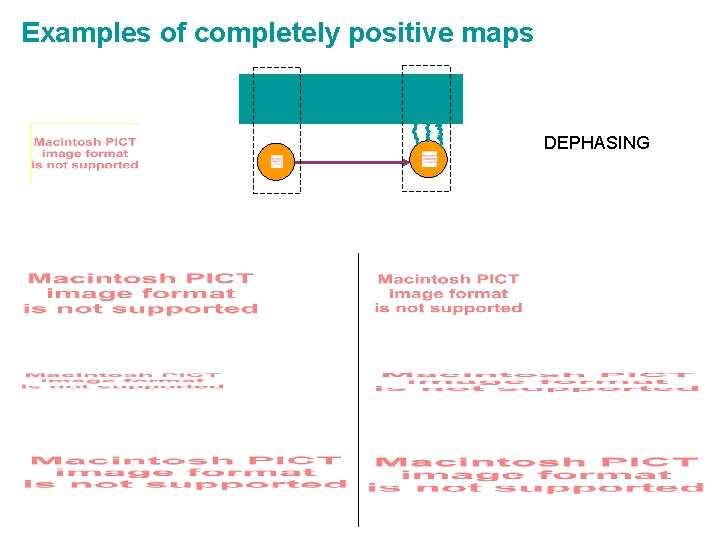
Examples of completely positive maps UNITARY DEPHASING

Examples of completely positive maps DEPHASING

Completely positive maps Hermitean trace preserved positive semidefinite

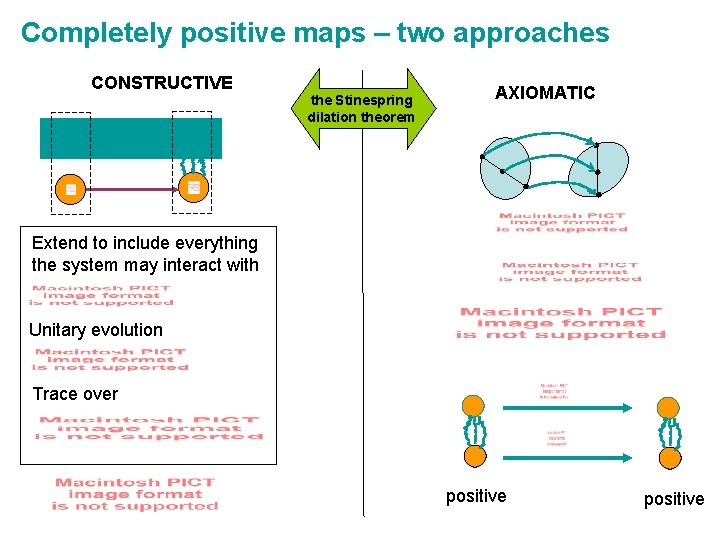
Completely positive maps – two approaches CONSTRUCTIVE the Stinespring dilation theorem AXIOMATIC Extend to include everything the system may interact with Unitary evolution Trace over positive

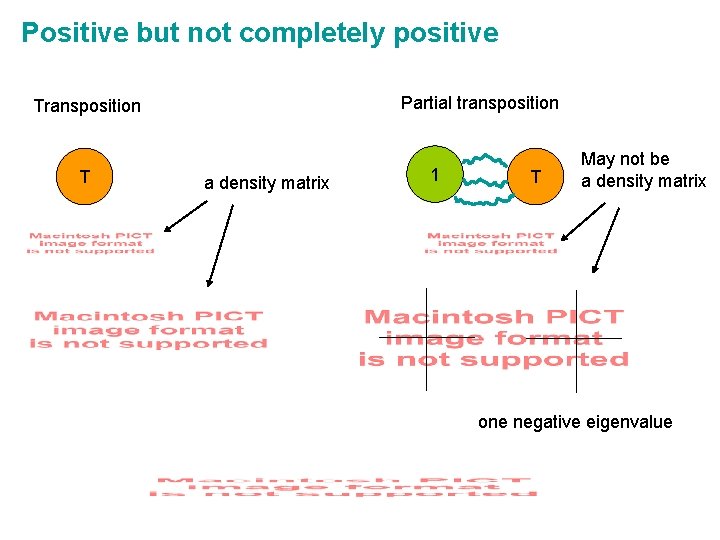
Positive but not completely positive Partial transposition T a density matrix 1 T May not be a density matrix one negative eigenvalue

Discrete errors

Discrete errors states of the environment are neither normalized nor mutually orthogonal

Few remarks does not imply (why? )

Discrete errors do nothing phase flip bit & phase flip

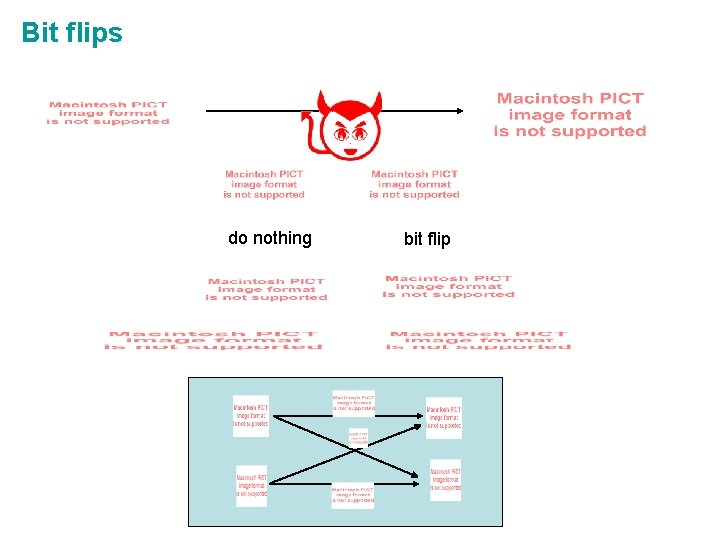
Bit flips do nothing bit flip

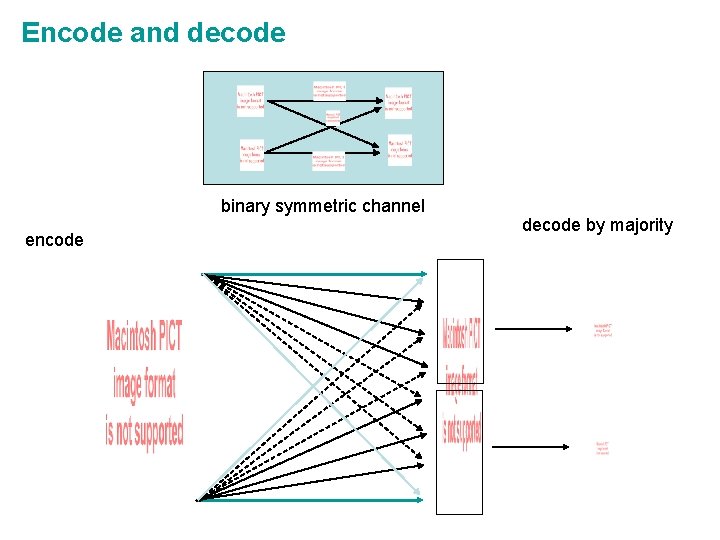
Encode and decode binary symmetric channel encode decode by majority

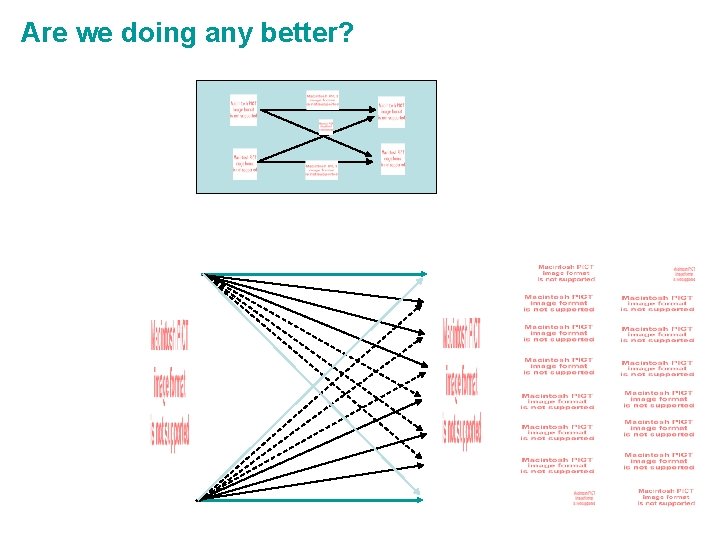
Are we doing any better?

Benefits of error correction no error one error two errors three errors If we can correct one error we reduce probability of error to

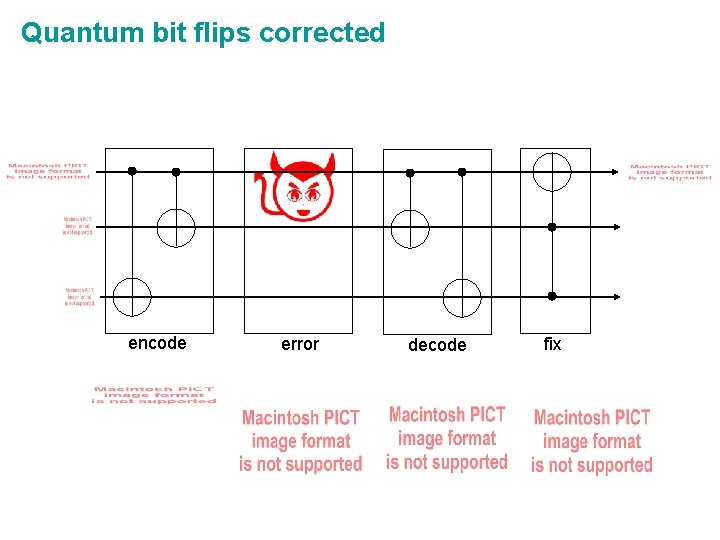
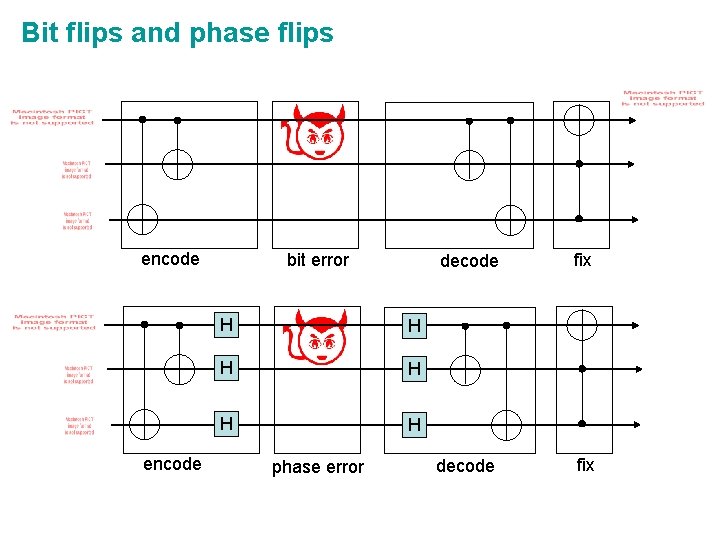
Quantum bit flips corrected encode error decode fix

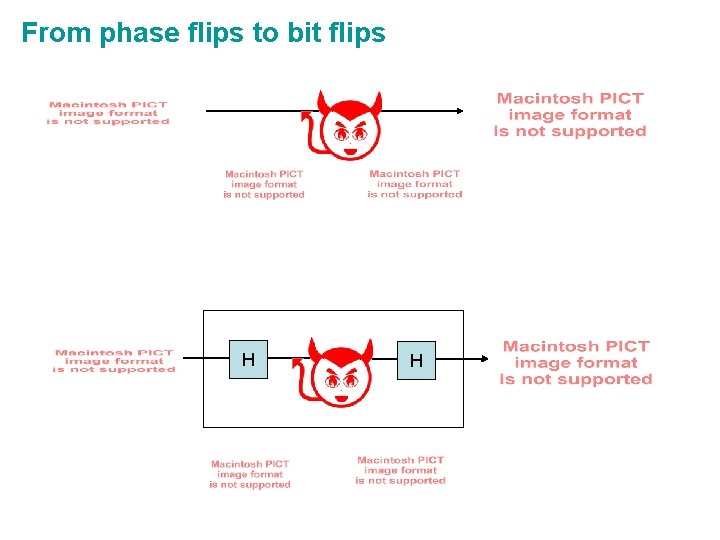
Phase flips do nothing phase flip reduction to bit flips

From phase flips to bit flips H H

Bit flips and phase flips encode bit error H H H phase error decode fix

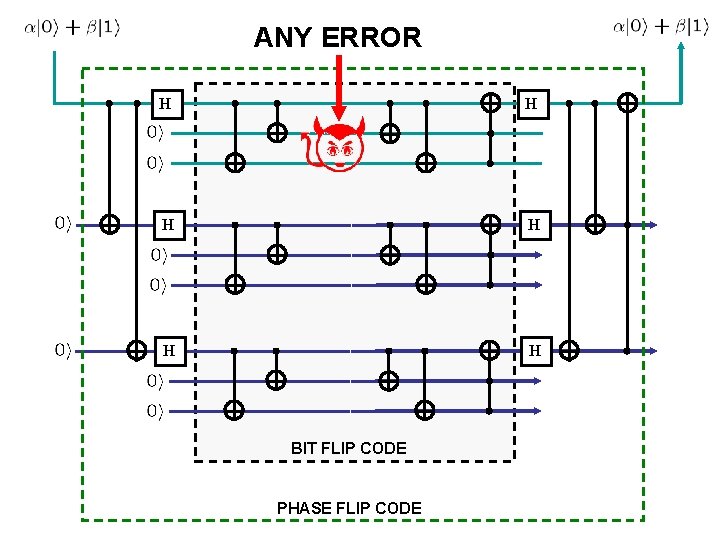
ANY ERROR H H H BIT FLIP CODE PHASE FLIP CODE