Aula Teorica 8 LUGAR GEOMETRICO DAS RAIZES Adio

Aula Teorica 8 LUGAR GEOMETRICO DAS RAIZES • • Adição de pólos e zeros ao LGR O Contorno das raízes O LGR de um sistema de segunda ordem variando razão de amortização Projecto de Controladores pelo metodo do LGR

Efeitos de adicionar pólos e zeros ao GH Em aulas posteriores aprenderemos a desenhar controladores usando o LGR e esse é um problema de modificar o lugar com adição de pólos e zeros por isso na aula de hoje veremos estes efeitos A adição de pólos (Explicaremos através de um exemplo) Considere a função LGR

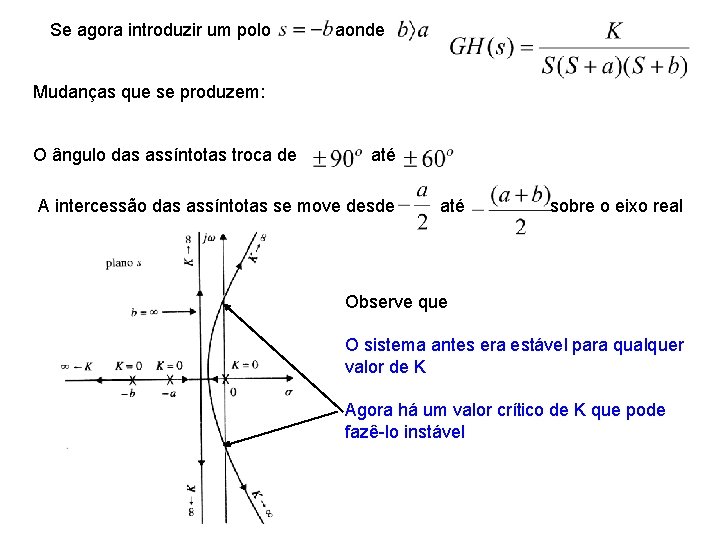
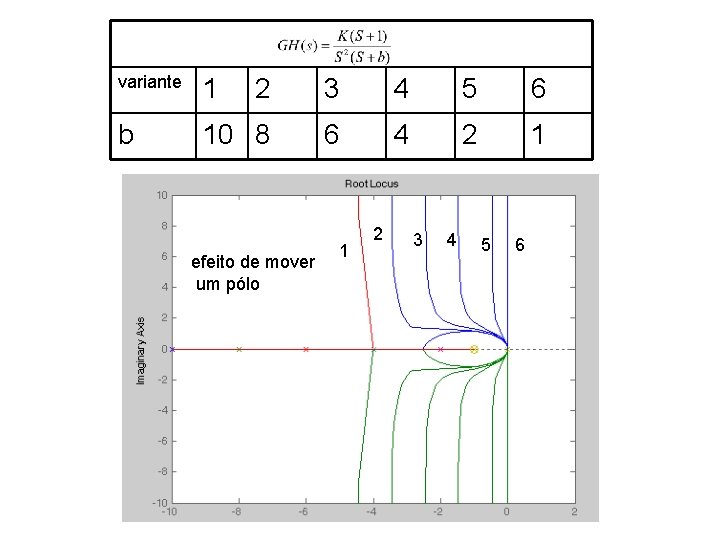
Se agora introduzir um polo aonde Mudanças que se produzem: O ângulo das assíntotas troca de até A intercessão das assíntotas se move desde até sobre o eixo real Observe que O sistema antes era estável para qualquer valor de K Agora há um valor crítico de K que pode fazê-lo instável

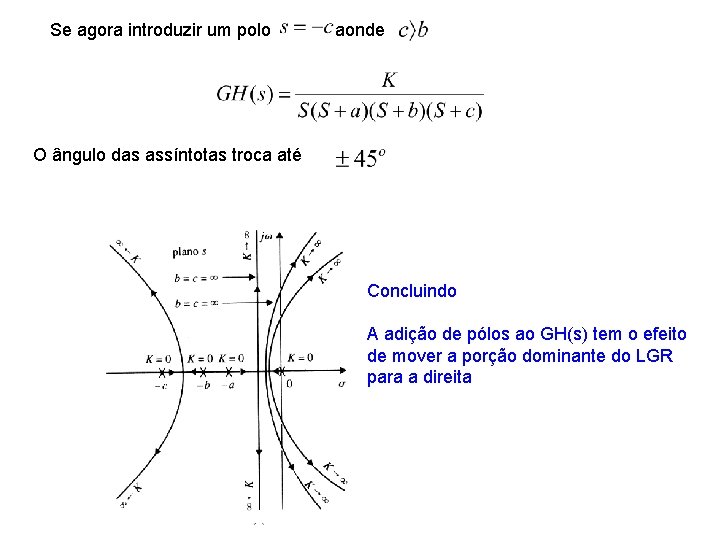
Se agora introduzir um polo aonde O ângulo das assíntotas troca até Concluindo A adição de pólos ao GH(s) tem o efeito de mover a porção dominante do LGR para a direita

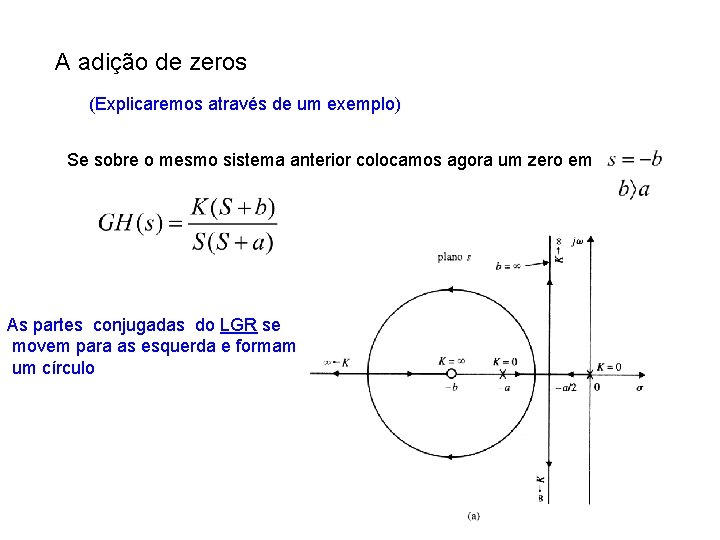
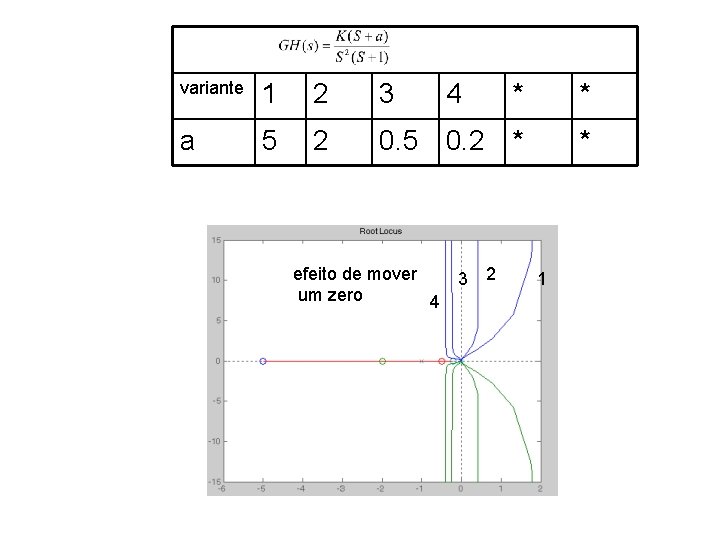
A adição de zeros (Explicaremos através de um exemplo) Se sobre o mesmo sistema anterior colocamos agora um zero em As partes conjugadas do LGR se movem para as esquerda e formam um círculo

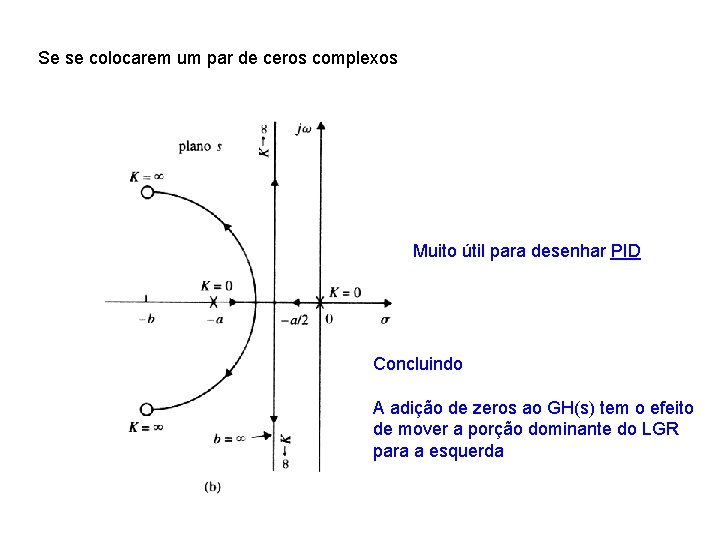
Se se colocarem um par de ceros complexos Muito útil para desenhar PID Concluindo A adição de zeros ao GH(s) tem o efeito de mover a porção dominante do LGR para a esquerda

variante 1 2 3 4 5 6 b 10 8 6 4 2 1 efeito de mover um pólo 1 2 3 4 5 6

variante 1 2 3 * * a 5 2 0. 5 0. 2 * * efeito de mover um zero 4 4 3 2 1

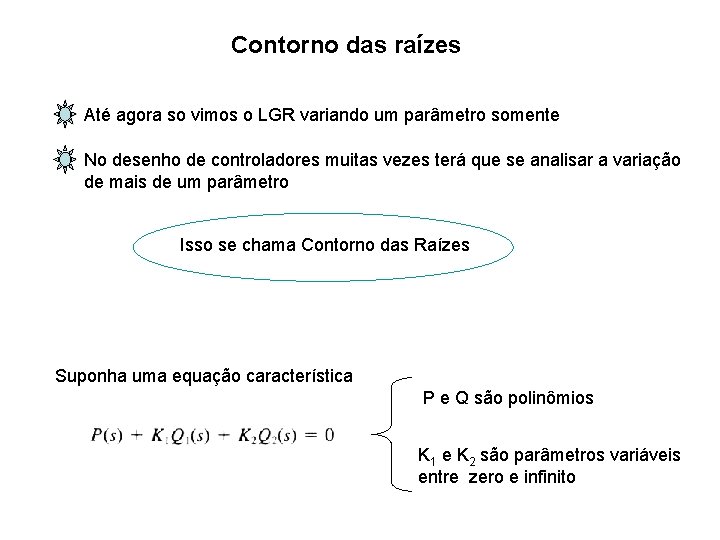
Contorno das raízes Até agora so vimos o LGR variando um parâmetro somente No desenho de controladores muitas vezes terá que se analisar a variação de mais de um parâmetro Isso se chama Contorno das Raízes Suponha uma equação característica P e Q são polinômios K 1 e K 2 são parâmetros variáveis entre zero e infinito

O procedimento é Primeiro faz um dos dois parâmetros zero K 2=0 Dividindo tudo por P Logo traça o LGR variando K 1(0→α) e estabelece dentro do lugar o valor que deseja que tenha K 1 Depois restaura o valor de K 2 enquanto considera que K 1 está fixo traça o LGR variando K 2 (0→α) (Explicaremos através de um exemplo)

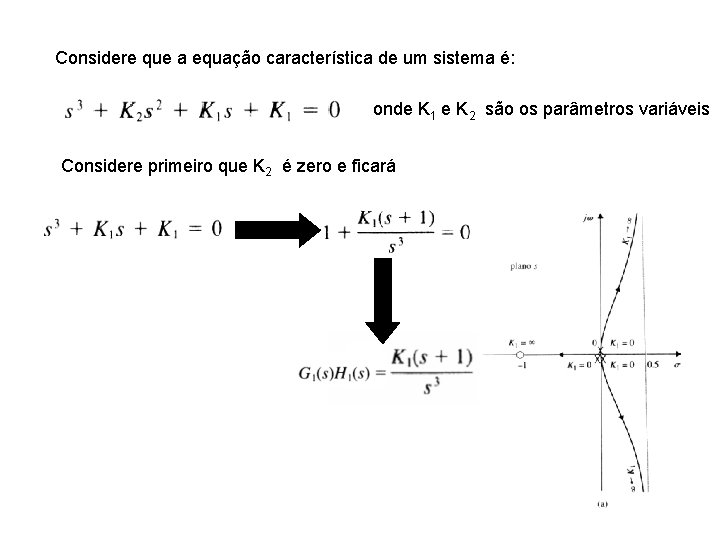
Considere que a equação característica de um sistema é: onde K 1 e K 2 são os parâmetros variáveis Considere primeiro que K 2 é zero e ficará

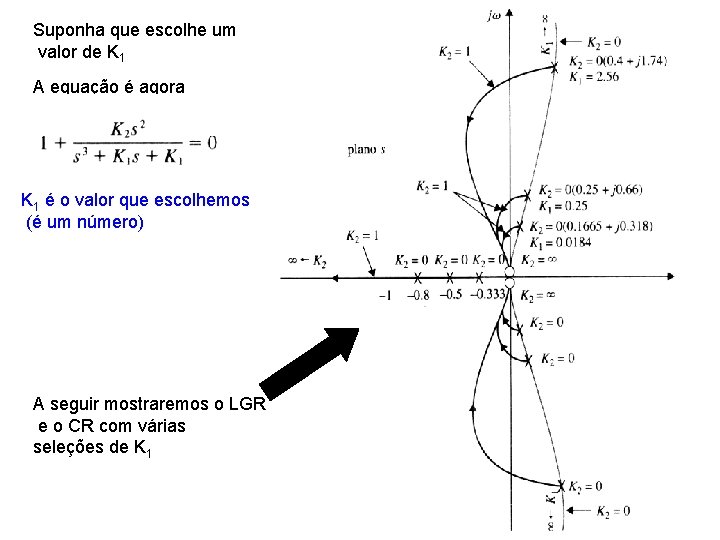
Suponha que escolhe um valor de K 1 A equação é agora K 1 é o valor que escolhemos (é um número) A seguir mostraremos o LGR e o CR com várias seleções de K 1

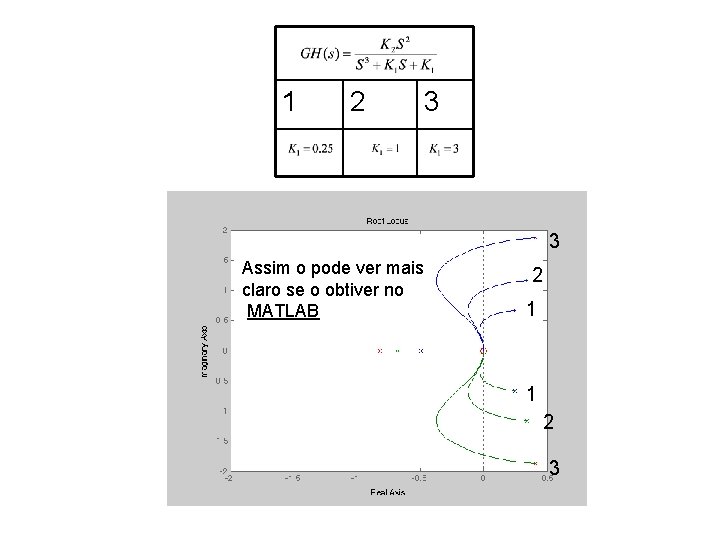
1 2 3 3 Assim o pode ver mais claro se o obtiver no MATLAB 2 1 1 2 3

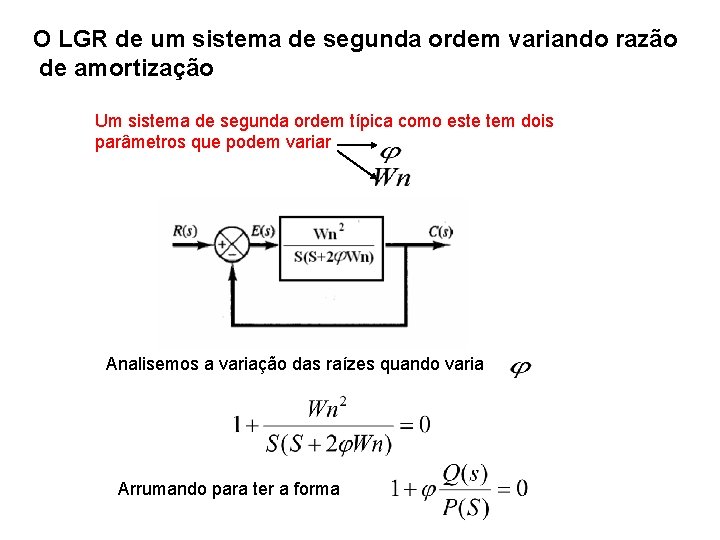
O LGR de um sistema de segunda ordem variando razão de amortização Um sistema de segunda ordem típica como este tem dois parâmetros que podem variar Analisemos a variação das raízes quando varia Arrumando para ter a forma

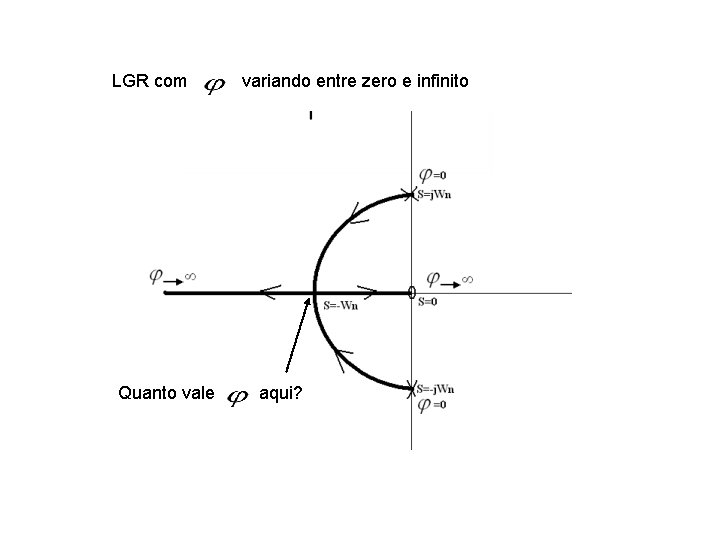
Esta é a equação com que faremos o LGR com variando entre zero e infinito

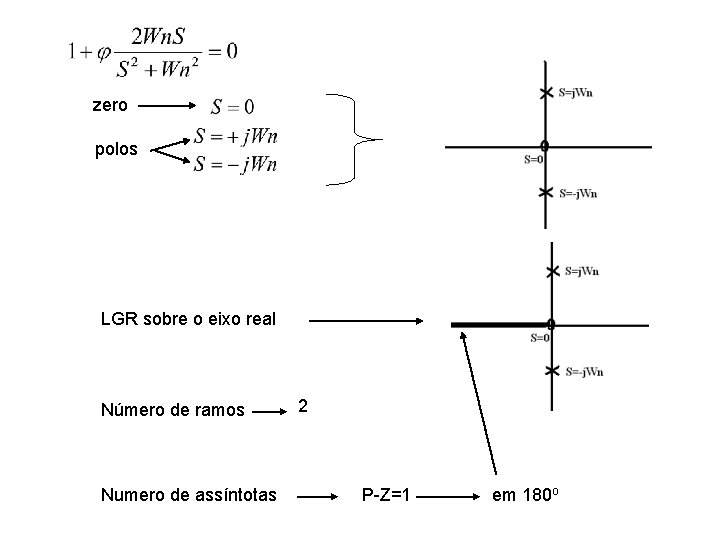
zero polos LGR sobre o eixo real Número de ramos Numero de assíntotas 2 P-Z=1 em 180 o

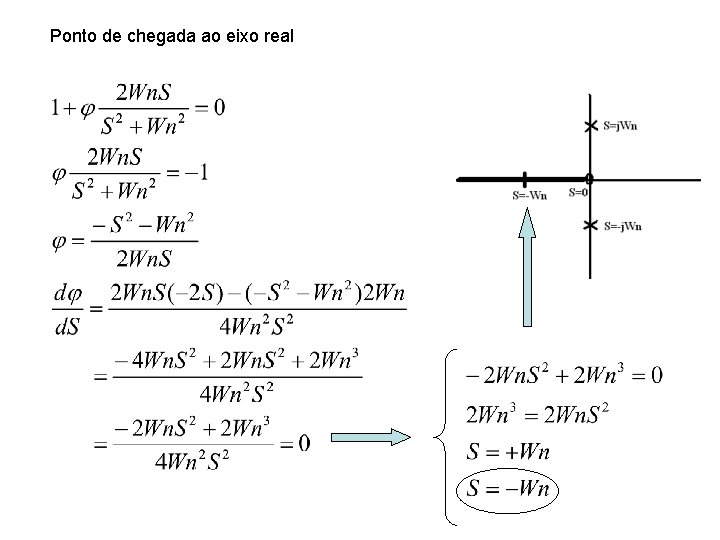
Ponto de chegada ao eixo real

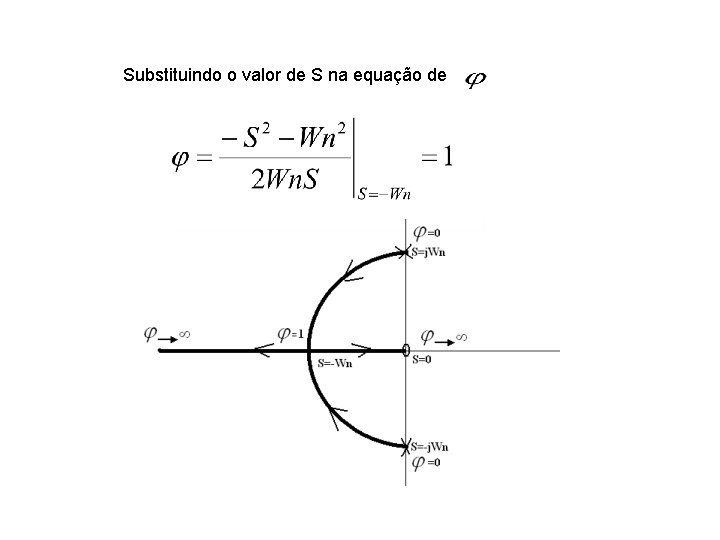
LGR com Quanto vale variando entre zero e infinito aqui?

Substituindo o valor de S na equação de

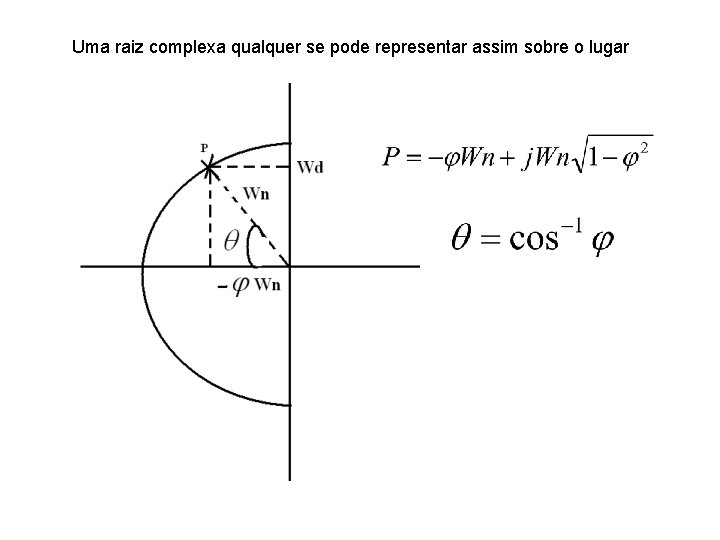
Uma raiz complexa qualquer se pode representar assim sobre o lugar

Concluindo Este conteúdo é útil no desenho de controladores que posteriormente veremos Nunca faremos estes traços à mãos, aprenderemos a fazê-lo no MATLAB

Intervalo

Recordar que

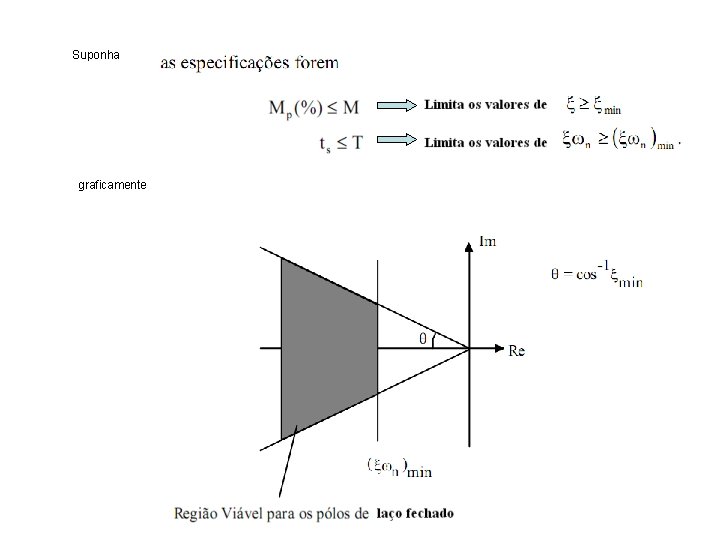
Suponha graficamente

Observações importantes Quando desejamos modificar o desempenho transitivo do sistema, as raízes da equação característica devem trocar portanto terá que modificar o LGR para que passe pelo ponto indicado conforme sejam as especificações Quando desejamos modificar o desempenho em estado estável, so utilizaremos o ganho do controlador sem variar muito o LGR

Só coloca um zero no LGR Projetar um PD é colocar adequadamente um zero

Estabelecimento ≥ 2. 17

Aplicando a condição de fase Que valor tomará Kc?

Aplicando a condição de magnitude Agora

Como fazer isto com o Matlab? G=tf(2, [1 0 0]) pd=-1+1. 95*j angcero=pi+angle(pd^2) zero=imag(pd)/tan(angcero)-real(pd) G 1=tf(2*[1 zero], [1 0 0]) rlocus(G 1) para achar o zero para achar Kd

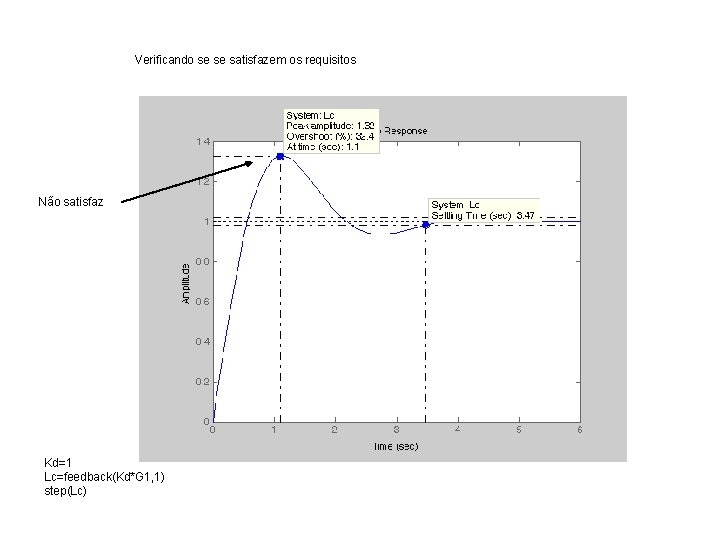
Verificando se se satisfazem os requisitos Não satisfaz Kd=1 Lc=feedback(Kd*G 1, 1) step(Lc)

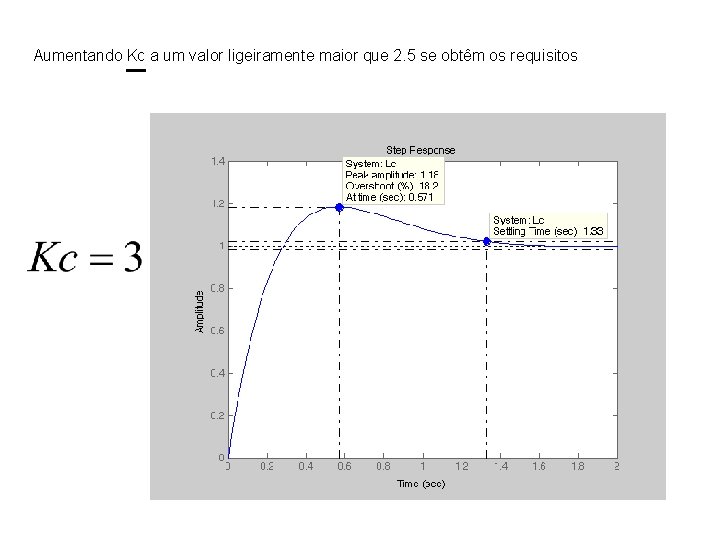
Aumentando Kc a um valor ligeiramente maior que 2. 5 se obtêm os requisitos

Coloca um pólo na origem e um zero em Sobre a origem não temos alternativas portanto o projeto se apóia em se localizar o zero

Tenha em conta que: Para que o estado transitório não se afete muito os pólos de laço fechado dominantes devem manter-se Quais são? Devido a que DEVEM MANTER-SE

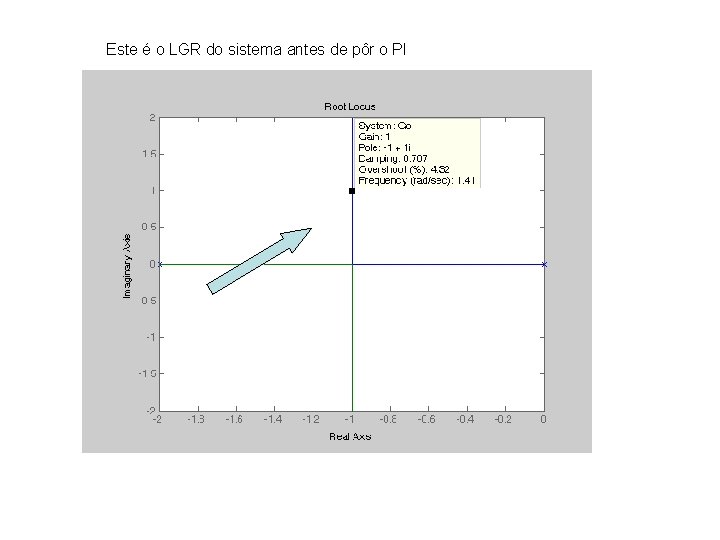
Este é o LGR do sistema antes de pôr o PI

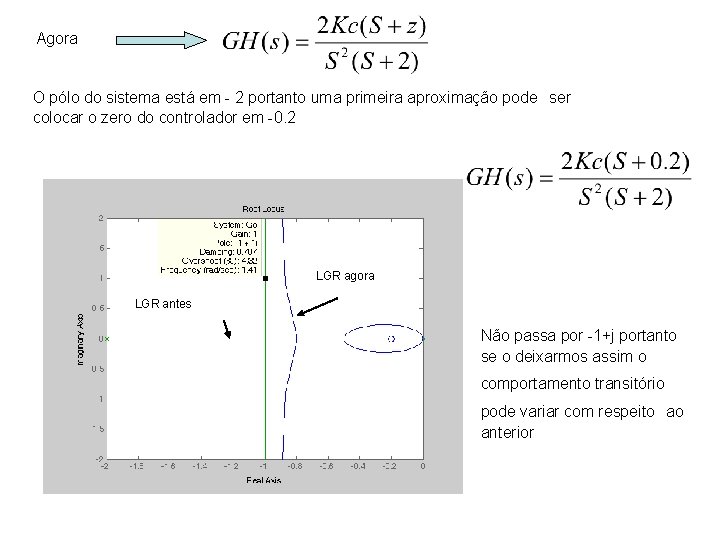
Agora O pólo do sistema está em - 2 portanto uma primeira aproximação pode ser colocar o zero do controlador em -0. 2 LGR agora LGR antes Não passa por -1+j portanto se o deixarmos assim o comportamento transitório pode variar com respeito ao anterior

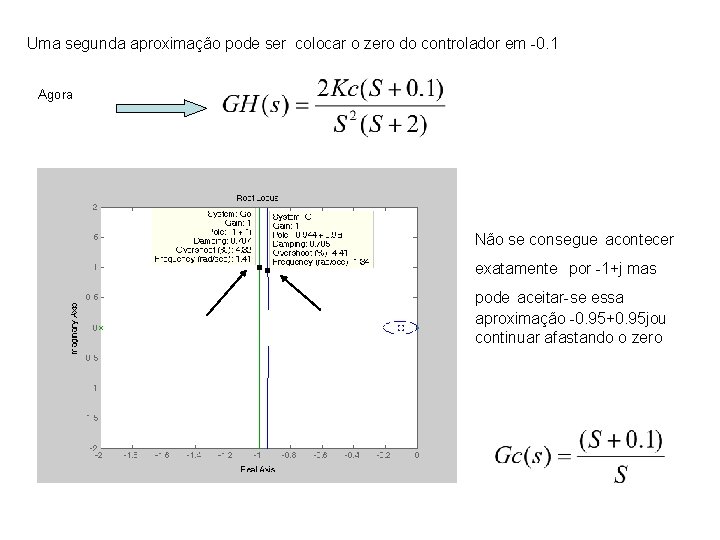
Uma segunda aproximação pode ser colocar o zero do controlador em -0. 1 Agora Não se consegue acontecer LGR antes LGR agora exatamente por -1+j mas pode aceitar-se essa aproximação -0. 95+0. 95 jou continuar afastando o zero

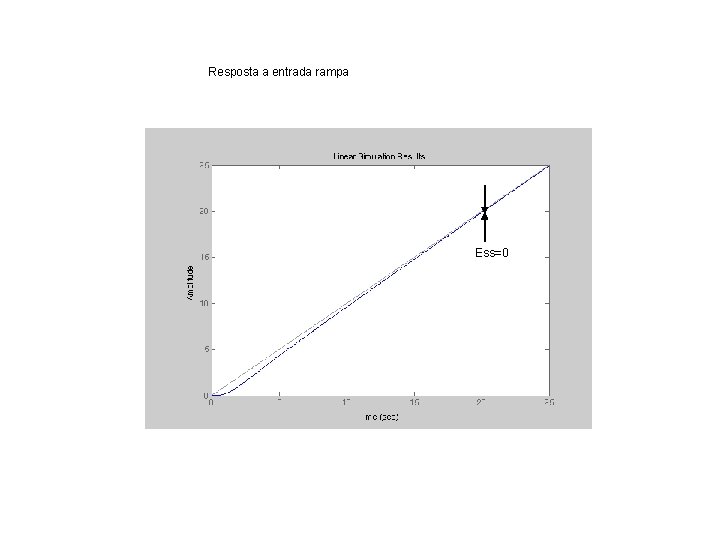
Resposta a entrada rampa Ess=0

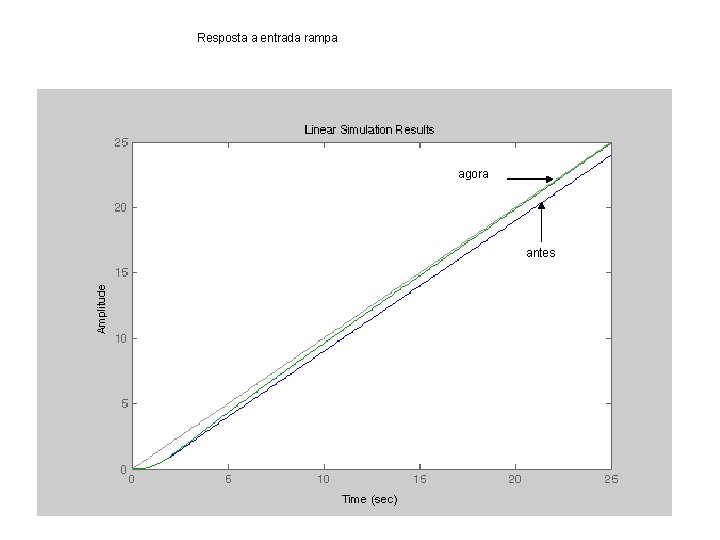
Resposta a entrada rampa agora antes

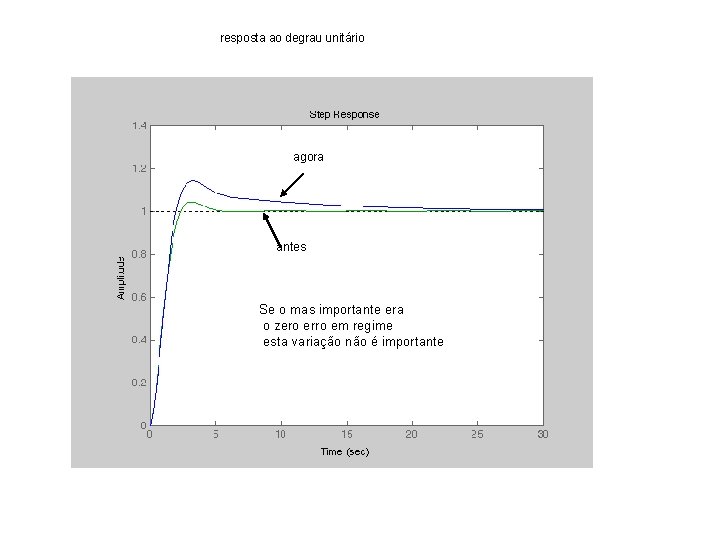
resposta ao degrau unitário agora antes Se o mas importante era o zero erro em regime esta variação não é importante

Coloca um pólo na origem e dois zeros

Não é a única

Em próxima atividade continuaremos com este tema mas em aula prática. Tragam os vossos computadores com MATLAB instalado