Resoluo de equaes no lineares Raiz de uma

Resolução de equações não lineares

Raiz de uma equação n Raiz exata ¨ Um número xr é raiz exata de uma equação f(x)=0 se f(xr)=0 n Raiz aproximada ¨ Um número x’ é raiz aproximada de uma equação f(x)=0 se |x’-xr| e |f(x’)| forem ambos próximos de 0 n Comparar o módulo da subtração da raiz é basicamente uma operação teórica, pois não se pode obter a raiz exata

Calculando as raízes Para calcular as raízes reais de uma equação f(x)=0 é necessário: n 1) delimitar, enumerar e separar as raízes n 2) utilizar um método numérico para calculo de cada raiz n

Equações algébricas polinomiais A) toda equação do tipo anxn+an-1 xn-1 +. . . a 1 x 1+a 0 é algébrica e polinomial n n é um número natural denominado grau da equação n Os coeficientes ai, i=0. . . n são números reais n

Equações algébricas polinomiais n Toda equação polinomial de grau n tem exatamente n raízes, reais ou complexas, desde que cada raiz seja contada de acordo com seu grau de multiplicidade

Multiplicidade de raizes Uma raiz tem grau de multiplicidade m se: n anula a função que origina a equação n n Anula as derivadas até a ordem m-1 n Não anula a derivada de ordem m

Exemplo A equação f(x)=x 3 -5 x 2+8 x-4 tem raízes x 1=1 x 2=2 e x 3=2 n f(2)=0 n f’(2) = 3 x 2 -10 x+8 -> f’(2)=0 n f’’(2)=6 x-10 ->f’’(2)=2 n

Equações algébricas polinomiais As raízes complexas aparecem sempre em pares conjugados (a+bi e a-bi) n Toda equação polinomial de grau impar tem pelo menos uma raiz real n

Delimitação de raízes reais n n n Limite superior positivo-teorema de Lagrange Seja f(x)=0 uma equação polinomial de grau n, na qual an>0 e a 0 ≠ 0 Para limite superior de suas raízes positivas, caso existam pode ser tomado o número K= grau do 1º termo negativo M= módulo do menor coeficiente negativo

Exemplo Calcule o limite superior para as raízes positivas da equação f(x) = x 5+x 4 -8 x 3 -16 x 2 +7 x+14 =0 n

Exemplo Calcule o limite superior para as raízes positivas da equação f(x) = x 5+x 4 -8 x 3 -16 x 2 +7 x+14 =0 n=5, k=3, a 5=1 e M=16 n

Delimitação das raízes reais Limite inferior negativo n Obter a equação auxiliar f 1(x)=f(-x)=0 n n n usar o teorema de Lagrange em f 1(x), obtendo o limite superior de suas raízes positivas L 1 O limite inferior das raízes negativas é dado por –L 1

Exemplo Calcule o limite inferior para as raízes negativas da equação f(x) = x 5+x 4 -8 x 3 -16 x 2 +7 x+14 =0 n

Exemplo f(x) = x 5+x 4 -8 x 3 -16 x 2 +7 x+14 =0 f 1(x) = -x 5+x 4+8 x 3 -16 x 2 -7 x+14 =0 an<0 logo devemos multiplicar f 1 por -1 f 1(x) = x 5 -x 4 -8 x 3+16 x 2+7 x-14 =0 n=5, k=4, a 5=1 e M=14 Logo –L 1=-15

Enumeração das raízes n Regra dos sinais de Descartes – O número de raízes positivas de equações polinomiais é igual ao número de variação de sinais apresentado pelo conjunto de coeficientes ou menor em um número par

Exemplo n x 5+x 4 -8 x 3 -16 x 2+7 x+14=0

Exemplo x 5+x 4 -8 x 3 -16 x 2+7 x+14=0 n

Exemplo x 5+x 4 -8 x 3 -16 x 2+7 x+14=0 n 2 variações -> 2 raízes ou nenhuma raiz n

Exemplo x 5 -x 4+8 x 3 -16 x 2+7 x-14=0 n Quantas raízes? n

Exemplo x 5 -x 4+8 x 3 -16 x 2+7 x-14=0 n Quantas raízes? n 5 variações -> 5 raízes ou 3 ou 1 raiz n

Exemplo 5 x 5 -16 x 2+7 x-14=0 n Quantas raízes? n

Exemplo 5 x 5 -16 x 2+7 x-14=0 n Quantas raízes? n 3 variações -> 3 raízes ou 1 raiz positiva n

Enumeração de raízes n Para determinar o número de raizes negativas basta trocar x por (-x) na equação e aplicar a regra dos sinais

Exemplo x 5+x 4 -8 x 3 -16 x 2+7 x+14=0 n f(-x)=-x 5+x 4+8 x 3 -16 x 2 -7 x+14=0 n 3 raízes ou 1 raiz negativa n

Exemplo x 5 -x 4+8 x 3 -16 x 2+7 x-14=0 n f(-x)=-x 5 -x 4 -8 x 3 -16 x 2 -7 x-14=0 n n Sem variação -> nenhuma raiz negativa

Sucessão de Sturm Dada a equação polinomial f(x)=0 a sucessão de Sturm a ela associada é o seguinte conjunto de polinômios: f(x)f 1(x)f 2(x). . . fm(x) n f(x) é o polinômio que origina a equação n f 1(x) é a primeira derivada de f(x) n

Sucessão de Sturm A partir de f 2(x) cada termo é o resto, com o sinal trocado, da divisão dos 2 termos anteriores n f(x)/f 1(x) = Q 1 x+R 1 x -> f 2(x)=-R 1 x n f 1(x)/f 2(x) = Q 2 x+R 2 x -> f 3(x)=-R 2 x n n A sucessão procede até que seja obtido um resto constante

Propriedades Se a equação tiver raízes múltiplas então o último termo da sucessão é nulo n Para nenhum valor de x, 2 termos consecutivos da sucessão não se anulam n Se, para algum x, um termo médio da sucessão se anula, então os termos vizinhos terão valores numéricos de sinais opostos n

Teorema de Sturm Seja N(alpha) o número de variações de sinal apresentado pela sucessão de sturm. Para x = alpha n O número de raízes reais de uma equação polinomial, sem raízes múltiplas, situadas em um intervalo [a, b] é igual a N(a)-N(b) n

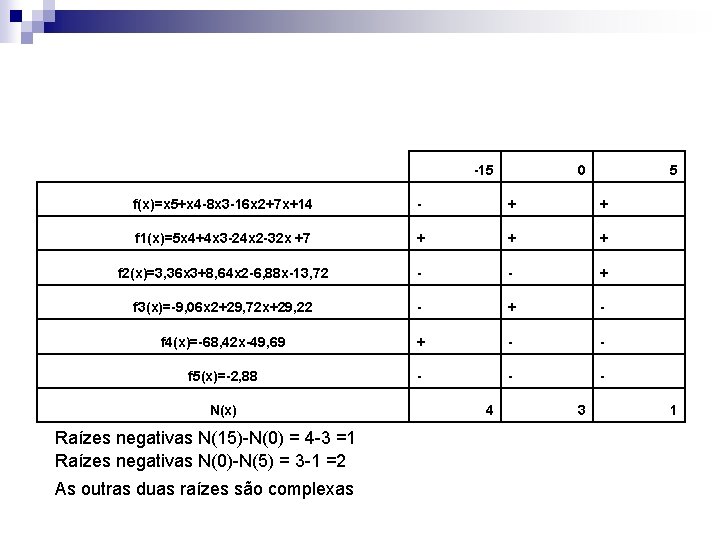
Exemplo n Determine o número de raízes reais da equação no intervalo (-15, 5) f(x)=x 5+x 4 -8 x 3 -16 x 2+7 x+14 f 1(x)=5 x 4+4 x 3 -24 x 2 -32 x+7 f 2(x)=3, 36 x 3+8, 64 x 2 -6, 88 x-13, 72 f 3(x)=-9, 06 x 2+29, 72 x+29, 22 f 4(x)=-68, 42 x-49, 69 f 5(x)=-2, 88

-15 0 5 f(x)=x 5+x 4 -8 x 3 -16 x 2+7 x+14 - + + f 1(x)=5 x 4+4 x 3 -24 x 2 -32 x +7 + + + f 2(x)=3, 36 x 3+8, 64 x 2 -6, 88 x-13, 72 - - + f 3(x)=-9, 06 x 2+29, 72 x+29, 22 - + - f 4(x)=-68, 42 x-49, 69 + - - f 5(x)=-2, 88 - - - N(x) Raízes negativas N(15)-N(0) = 4 -3 =1 Raízes negativas N(0)-N(5) = 3 -1 =2 As outras duas raízes são complexas 4 3 1

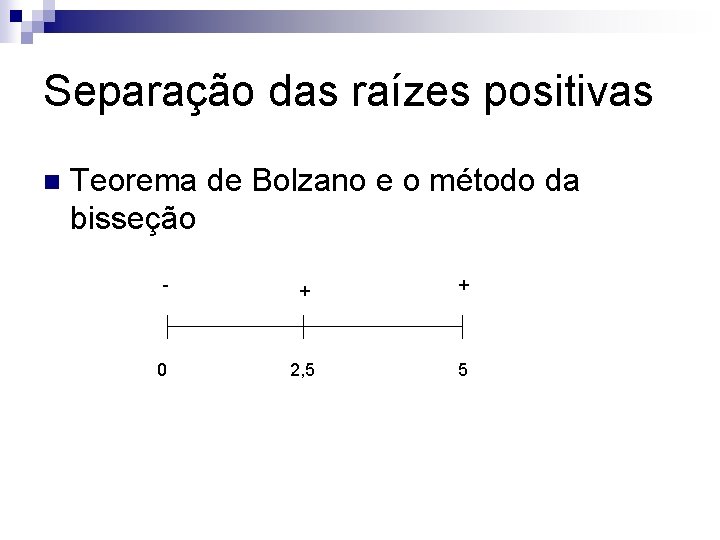
Separação de Raízes reais Teorema de Bolzano: seja f(x) uma função continua em um intervalo [a, b] n Se f(a). f(b)<0 então a equação f(x)=0 tem um número impar de raízes no intervalo [a, b] n

Exemplo

Exemplo

Separação de Raízes reais n Se f(a). f(b) >0 então f(x)=0 tem um número par de raízes ou nenhuma raiz no intervalo [a, b]

Exemplo

Exemplo

Exemplo

Exemplo

Exemplo Separe as raízes positivas da equação n f(x)= x 5+x 4 -8 x 3 -16 x 2+7 x+14=0 n Sabendo-se que estão situadas no intervalo (0, 5) e que o número de raízes positivas é 2 n

f(0)=14, f(5)=2399, f(2, 5)= -56, 78 n Uma raiz entre 0 e 2, 5 e outra entre 2, 5 e 5 n

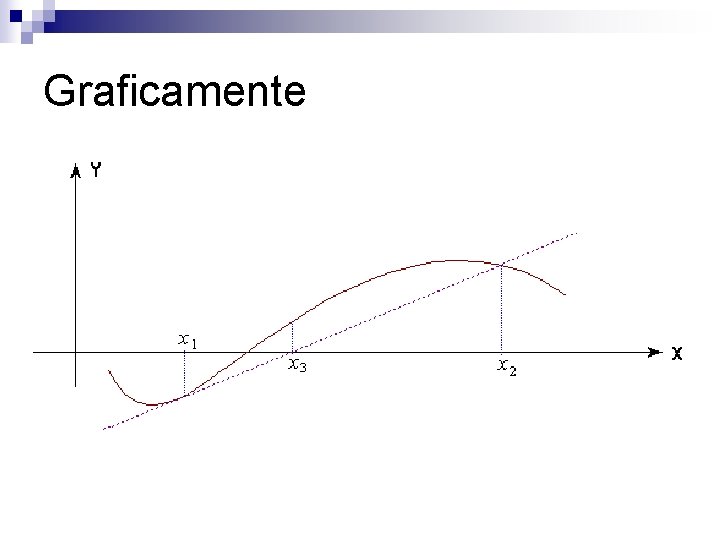
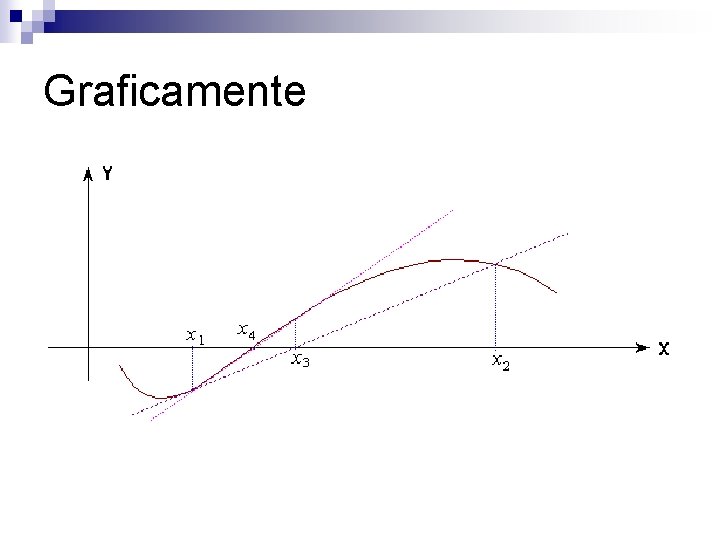
Equações não polinomiais Duas possibilidades n 1) Construir um esboço do gráfico da função com o objetivo de detectar os pontos n 2) Transformar a equação f(x)=0 em uma equação equivalente da forma g(x)-h(x)=0 n g(x)=h(x) n

Equações não polinomiais Esboçar os gráficos de g(x) e h(x) em um mesmo sistema de eixos cartesianos n As abscissas de cada ponto onde g(x) e h(x) se interceptam é uma raiz de f(x) n

Exemplo Seja a equação f(x)=x+ -5=0 n Pode ser escrita = 5 -x (g(x)=h(x)) n

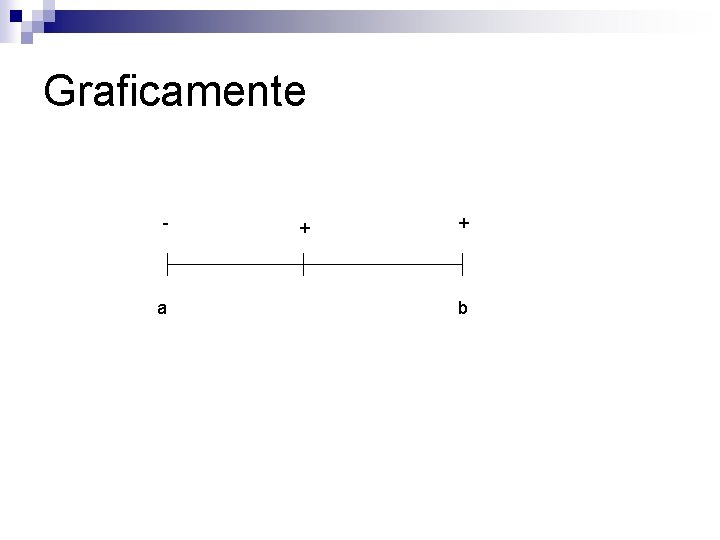
Metodo da Bisseção Seja f(x) uma função continua em um intervalo [a, b] n O intervalo contém uma única raiz da equação f(x)=0 sendo assim, f(a). f(b)<0 n Este método consiste em dividir de forma sucessiva o intervalo [a, b] ao meio, até que seja obtido (b-a) <= precisão estabelecida n

Graficamente - + a b

Graficamente - a + + b

Graficamente - a + b’ + b

Graficamente - a - + b’ + b

Graficamente - - a a’ + b

Critério de parada O processo para quando o intervalo [a, b] é suficientemente pequeno n Assim qualquer ponto no intervalo é tomado como raiz n Número máximo de passos – préestabelecido n

Convergência Sendo f(x) contínua em [a, b] n f(a). f(b)<0 n n O método da bisseção converge se as condições anteriores forem respeitadas

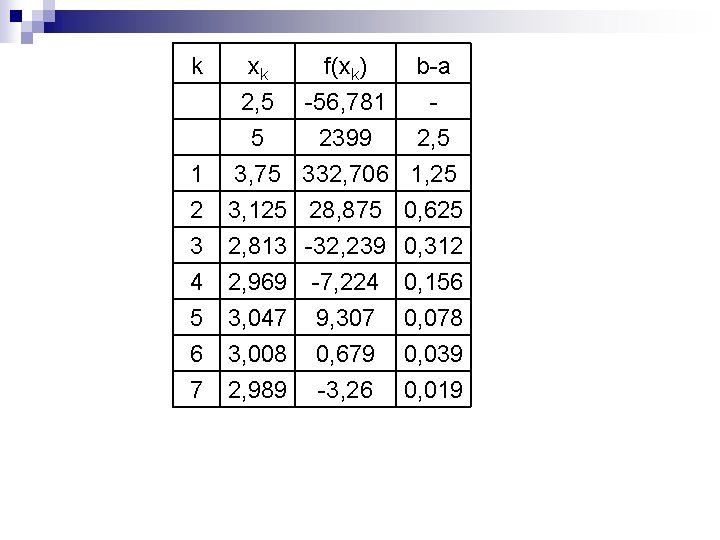
Exemplo Utilizando o método da bisseção calcule a maior raiz positiva da equação n f(x)= x 5+x 4 -8 x 3 -16 x 2+7 x+14=0 n Precisão 0, 025, máximo de 10 iterações, intervalo = [2, 5; 5] n f(2, 5)=-56, 781 e f(5)=2399 n

k xk f(xk) b-a 1 2, 5 -56, 781 5 2399 2, 5 3, 75 332, 706 1, 25 2 3 4 5 6 7 3, 125 28, 875 0, 625 2, 813 -32, 239 0, 312 2, 969 -7, 224 0, 156 3, 047 9, 307 0, 078 3, 008 0, 679 0, 039 2, 989 -3, 26 0, 019

n Qualquer número no intervalo [2, 989; 3, 008] pode ser tomado como raiz

Método da Falsa Posição Seja f(x) uma função contínua em um intervalo [a, b] que contém um e só uma raiz da equação f(x)=0 n Este método consiste em dividir o intervalo [a, b] no ponto onde a reta que passa pelos pontos (a, f(a)) e (b, f(b)) intercepta o eixo das abscissas n

Graficamente

Graficamente

Critério de parada n O processo iterativo é interrompido quando for obtido |f(xk)|, k=1, 2, . . . Menor ou igual à precisão estabelecida e então xk é tomado como raiz

Critério de convergência n Se f(x) é contínua em [a, b] e f(a). f(b)<0, então o método da falsa posição converge

Calculando xk n No método da bisseção x é dado pela média aritmética do intervalo x= (a+b)/2 No método da FP o x é dado pela média aritmética ponderada n x=(a|f(b)|+b|f(a)|)/(|f(b)|+|f(a)|) n x=(af(b)-bf(a))/(f(b)-f(a)) n

O cálculo de xk n Seja a matriz bf(a) +x 1 f(b)-af(b)-x 1 f(a) n x 1=(af(b)-bf(a))/(f(b)-f(a)) n

Generalizando xk=(af(b)-bf(a))/(f(b)-f(a)) n Desde que a cada passo seja atualizado a ou b n O critério utilizado por este método para a divisão do intervalo [a, b] é o da média ponderada n

Exemplo Utilizando o método da falsa posição com precisão 0. 006 e um máximo de 5 iterações encontrar a maior raiz positiva n f(x)=x 4 -14 x 2+24 x-10=0 n A) delimitação das raízes reais n LSP = = 4, 7 = 5 n

LIN – equação auxiliar n f(x) = x 4 -14 x 2 -24 x-10 n L 1=6 n Logo –L 1=-6 n

Enumeração das raízes reais Raízes positivas: +1 -14+24 -10 n 3 variações -> 3 ou 1 raiz positiva n Raízes negativas: +1 -14 -24 -10 n 1 variação -> 1 raiz negativa n

Número de raízes positivas n Teorema de Sturm Sucessão de Sturm 0 5 f(x)=x 4 -14 x 2+24 x-10 - + f 1(x)=4 x 3 -28 x+24 + + f 2(x)=7 x 2 -18 x+10 + + f 3(x)=7, 24 x-9, 3 - + f 4(x)=1, 5 + + N(x) 3 0

Número de raízes positivas n O número de raízes é dado por: N(0)-N(5)=3 -0=3

Separação das raízes positivas n Teorema de Bolzano e o método da bisseção - + 0 5

Separação das raízes positivas n Teorema de Bolzano e o método da bisseção - + + 0 2, 5 5

Separação das raízes positivas n Teorema de Bolzano e o método da bisseção - + + 0 1, 25 2, 5 3, 75 5

Separação das raízes positivas n Teorema de Bolzano e o método da bisseção - 0 - - + 1, 25 0, 625 1, 875 + + + 2, 5 3, 75 5

Calculando a maior raiz positiva Reduzindo um pouco mais o intervalo n f(1, 875)<0, f(2, 5)>0, f(2, 188)<0 n Aplicando o método da falsa posição n xk=(af(b)-bf(a))/(f(b)-f(a)) n

k a b f(a) f(b) xk f(xk) 1 2, 188 2, 5 -1, 592 1, 563 2, 345 -0, 467 2 2, 345 2, 5 -0, 467 1, 563 2, 381 -0, 085 3 2, 381 2, 5 -0, 085 1, 563 2, 387 -0, 016 4 2, 387 2, 5 -0, 016 1, 563 2, 388 -0, 005 Para a precisão estabelecida, 2, 388 é a maior raiz positiva da equação

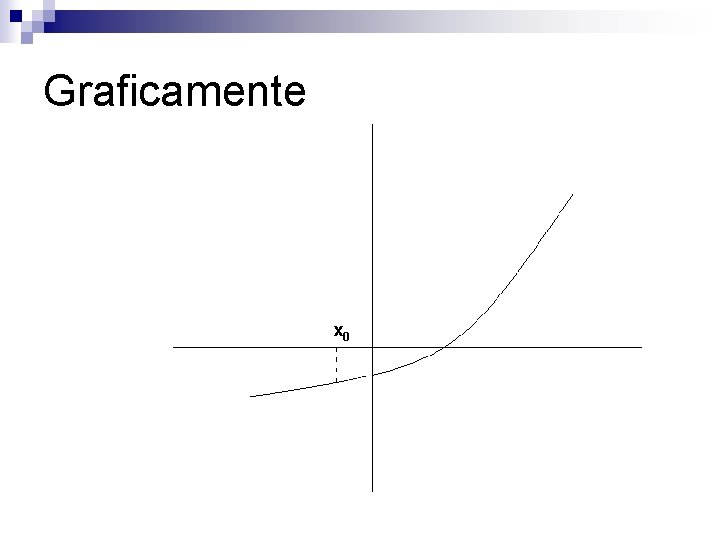
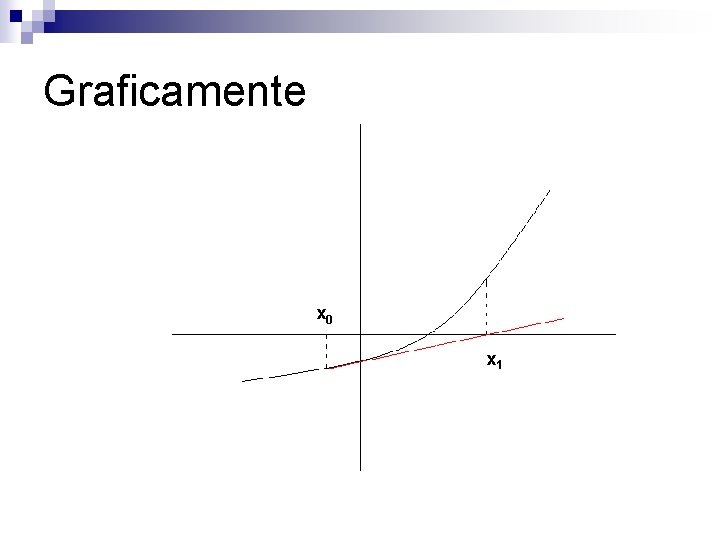
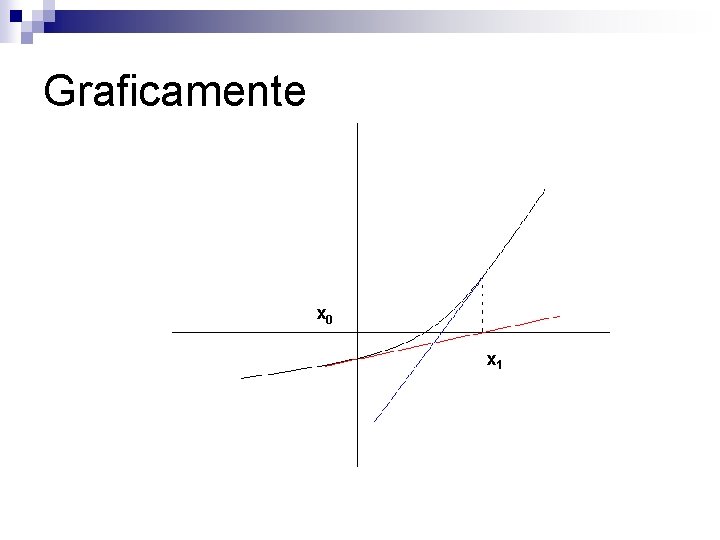
Método de Newton-Raphson Também conhecido como método das tangentes n Seja f(x) uma função contínua em um intervalo [a, b] que contém uma e só uma raiz da equação f(x)=0 n

Método de Newton-Raphson n Dada uma estimativa xk-1, k=1, 2, . . . , para uma raiz de f(x)=0 a estimativa xk é a abscissa do ponto onde a reta tangente f(x) em [xk-1, f(xk-1)] intercepta o eixo das abscissas

Método de Newton-Raphson n Critério de parada: O processo é interrompido quando for obtido um |xk-xk-1| ou |f(xk)| menor ou igual a uma precisão pré-estabelecida

Graficamente x 0 x 1

Graficamente x 0 x 1

Graficamente x 0 x 1

Método de Newton-Raphson n Convergência: se f(a)f(b)<0 e f’(x) e f’’(x) forem não nulas e mantiverem o sinal em [a, b], então partindo-se de uma estimativa inicial x 0 є[a, b] tal que f(x 0)f’’(x)>0 é possível construir, pelo método de Newton -Raphson uma sequência {xk}, k=1, 2, . . . , que converge para a raiz de f(x)=0

Método de Newton-Raphson n Seja o cálculo de x 1 n Para x 2

Método de Newton-Raphson n Generalizando

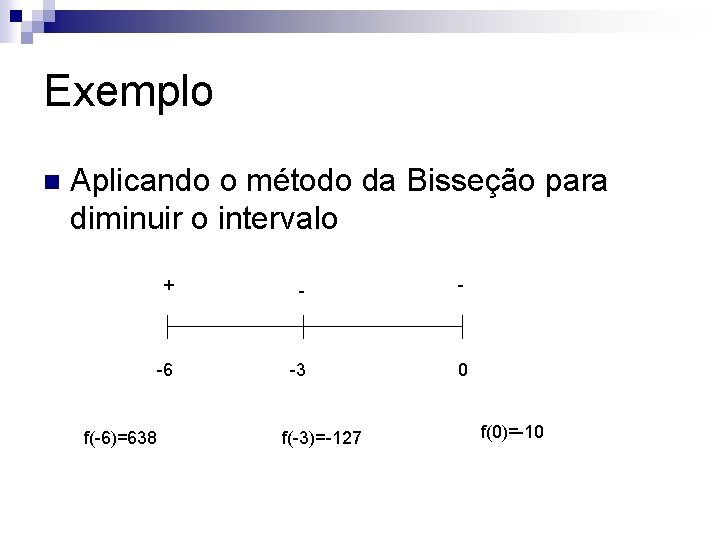
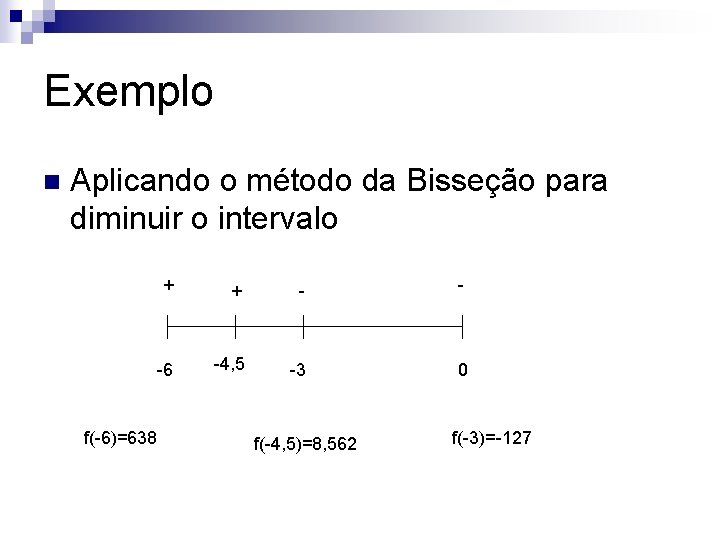
Exemplo n Calcule a raiz negativa de f(x)=x 414 x 2+24 x-10=0 utilizando o método de newton-Raphson com precisão 0, 001 e um máximo de 5 iterações. Sabe-se que esta raiz está situada no intervalo (-6, 0)

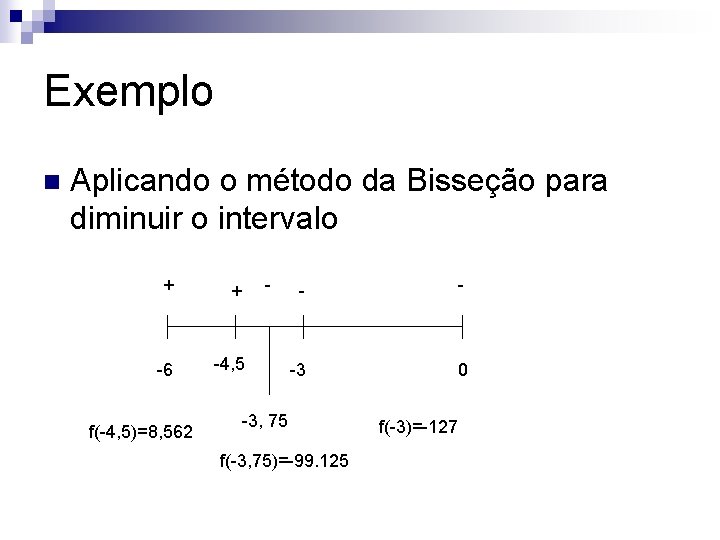
Exemplo n Aplicando o método da Bisseção para diminuir o intervalo f(-6)=638 + - -6 0 f(0)=-10

Exemplo n Aplicando o método da Bisseção para diminuir o intervalo f(-6)=638 + - - -6 -3 0 f(-3)=-127 f(0)=-10

Exemplo n Aplicando o método da Bisseção para diminuir o intervalo f(-6)=638 + + - - -6 -4, 5 -3 0 f(-4, 5)=8, 562 f(-3)=-127

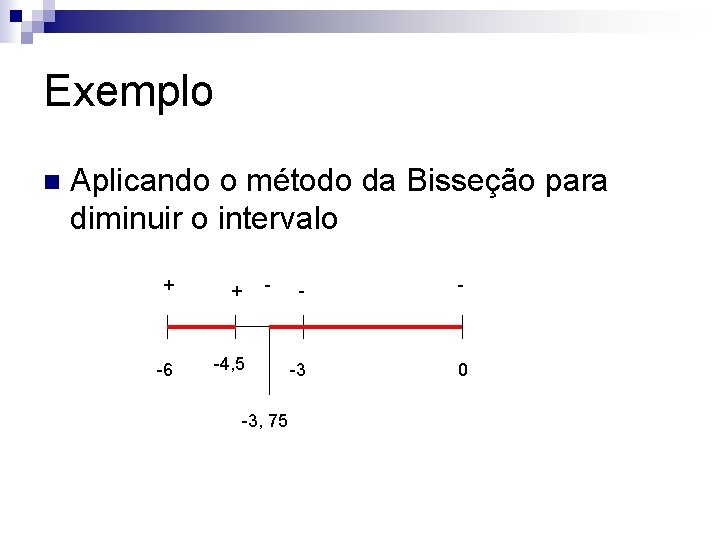
Exemplo n Aplicando o método da Bisseção para diminuir o intervalo + + -6 -4, 5 f(-4, 5)=8, 562 - -3 0 -3, 75 f(-3, 75)=-99. 125 f(-3)=-127

Exemplo n Aplicando o método da Bisseção para diminuir o intervalo + + - -6 -4, 5 -3, 75 - - -3 0

Exemplo n f’(x)=4 x 3 -28 x+24 <0 no intervalo [-4, 5; -3, 75] n f’’(x)=12 x 2 -28 >0 no intervalo [-4, 5; -3, 75] n Como f(-4, 5)f’’(-4, 5)>0 então x 0=-4, 5

Exemplo k xk f(xk) f'(xk) |xk-xk-1| 0 -4, 5 8, 562 -214, 5 - 1 -4, 460 0, 153 -205, 986 2 -4, 459 0, 018 0, 040 0, 001

Notas Com relação à convergência o que se faz na prática é: n 1) toma-se uma estimativa inicial próxima da raiz; para isto basta diminuir suficientemente o intervalo que a contém n 2) toma-se x 0 є [a, b] de forma que seja obtido x 1 є [a, b] n

Comparação - Bisseção Apesar de sempre convergir, tem baixa velocidade de convergência n Utilizado de forma isolada quando se deseja um intervalo, tal que qualquer dos pontos pode ser tomado como raiz n Normalmente é utilizado para reduzir o tamanho do intervalo que contém a raiz n

Comparação – F. P. e N. R. Quando se deseja é um intervalo que contém a raiz o método da Falsa Posição não é adequado porquê não converge n Quando não houver problemas para trabalhar com a primeira derivada de f(x) deve-se usar o método de Newton. Raphson; caso contrário deve-se usar o método da Falsa Posição n

Exercício n Determine os limites das raízes reais da equação f(x)=x 3+4 x 2 -10=0