Analysis mehr als Tangenten und Flchen ein anwendungsorientierter

Analysis – mehr als Tangenten und Flächen ein anwendungsorientierter Einstieg in die Analysis mit CAS Michael Rüsing B. M. V. – Schule Bardelebenstraße 9 45147 Essen michael@ruesing-essen. de

Voraussetzungen Änderungsrate ist bei linearen Funktionen bekannt Intuitiver Grenzwertbegriff ist vorhanden

Einstiegsaufgabe zur Differentialrechnung Schilderung eines Problemzusammenhangs An einer meteorologischen Messstation werden verschiedene Wetterdaten erhoben. Unter anderem wird auch die Regenmenge registriert. In einem oben offenen Glasrohr kann abgelesen werden, wie hoch der Regenwasserstand ist. Wird zu verschiedenen Zeitpunkten die Höhe des Wasserstandes registriert, ergibt sich eine Wasserstandsfunktion. Mit Hilfe dieser Funktion lassen sich eine ganze Reihe von Fragen beantworten.

Die Höhe des Wasserstandes sei gegeben durch die Funktion mit der Gleichung Dabei wird h in cm und t in Stunden gemessen Wie hoch steht das Wasser nach 8 Stunden? Wann steht das Wasser 5 cm hoch? Um wie viel ist der Wasserstand von 10 Uhr bis 11 Uhr gestiegen?

Die Höhe des Wasserstandes sei gegeben durch die Funktion mit der Gleichung Dabei wird h in cm und t in Stunden gemessen Hat es um 15. 00 Uhr stärker geregnet oder um 16. 00 Uhr?

Erster Lösungsansatz Also hat es um 16. 00 stärker geregnet. Zweiter Lösungsansatz In der 16. Stunde ist mehr Regen gefallen als in der 17.

Dritter Lösungsansatz Die Werte werden so klein und sind nicht mehr miteinander vergleichbar. Wie entscheidet man, ob es von 15 bis 15, 5 heftiger geregnet hat als von 15 bis 15, 1? Wähle ein gemeinsame Bezugsgröße, etwa eine Stunde: wird verglichen mit

Verallgemeinerung Bisher berechnet: durchschnittliche Regenheftigkeit in Intervallen Beobachtung: Je kürzer das Intervall, desto besser stimmt der Durchschnittswert mit der Heftigkeit des Regens zu dem gewünschten Zeitpunkt überein. Erinnerung: Grenzwertbildung

Term (unendlich viele Durchschnittswerte) als Voraussetzung für Grenzwertbildung Im Unterricht beobachtete Alternativen Alle Alternativen sind brauchbar

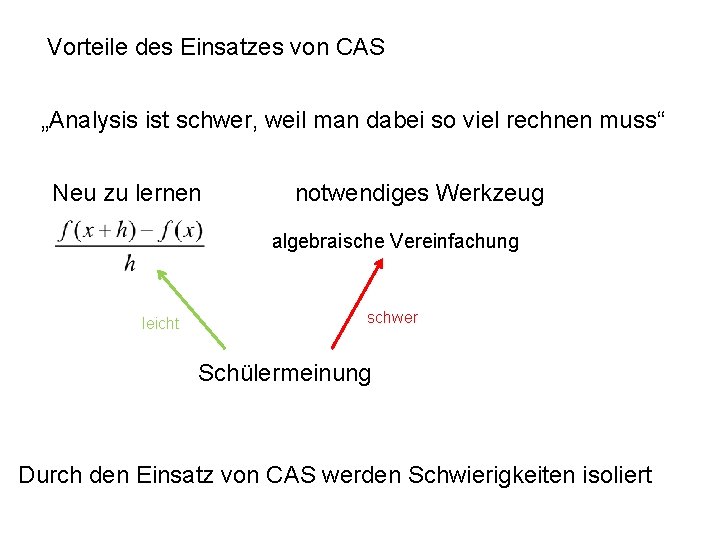
Vorteile des Einsatzes von CAS „Analysis ist schwer, weil man dabei so viel rechnen muss“ Neu zu lernen notwendiges Werkzeug algebraische Vereinfachung leicht schwer Schülermeinung Durch den Einsatz von CAS werden Schwierigkeiten isoliert

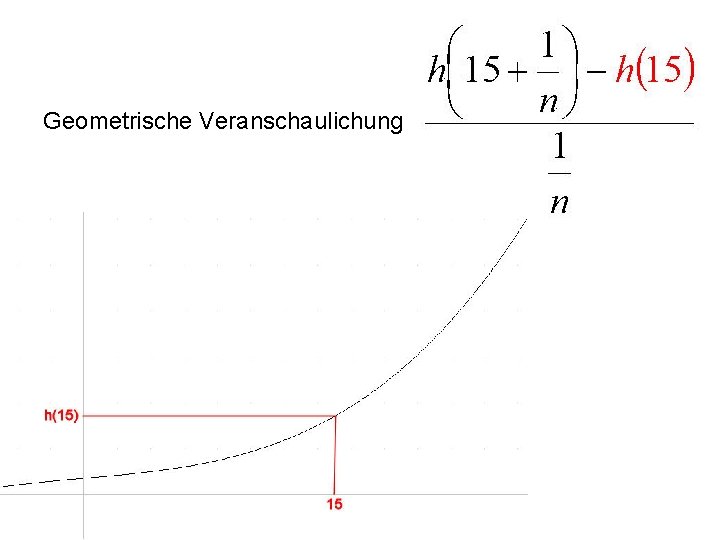
Kombinieren der Schwierigkeiten Bei welchen Funktionstypen sollen die Schüler die Umformung des Differenzenquotienten ohne Technologie leisten? Zu welchem Zeitpunkt soll das geschehen? Klausuraufgabe: Gegeben ist die Funktion mit der Gleichung Bestimmen Sie als Grenzwert ohne Technologie

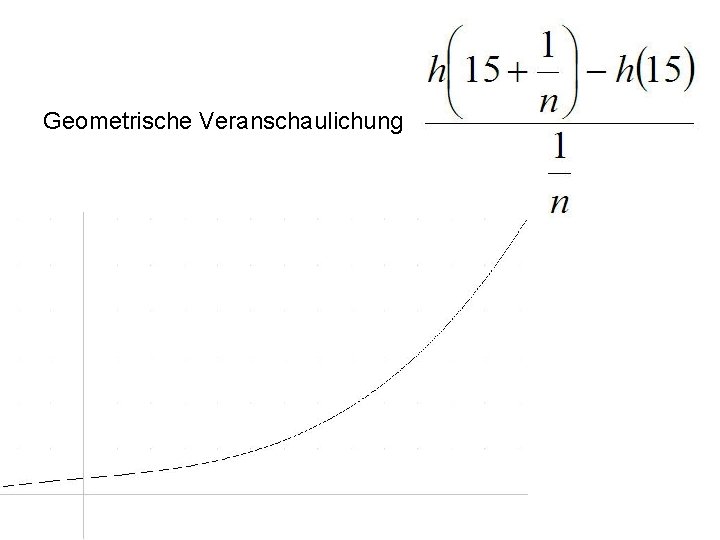
Geometrische Veranschaulichung

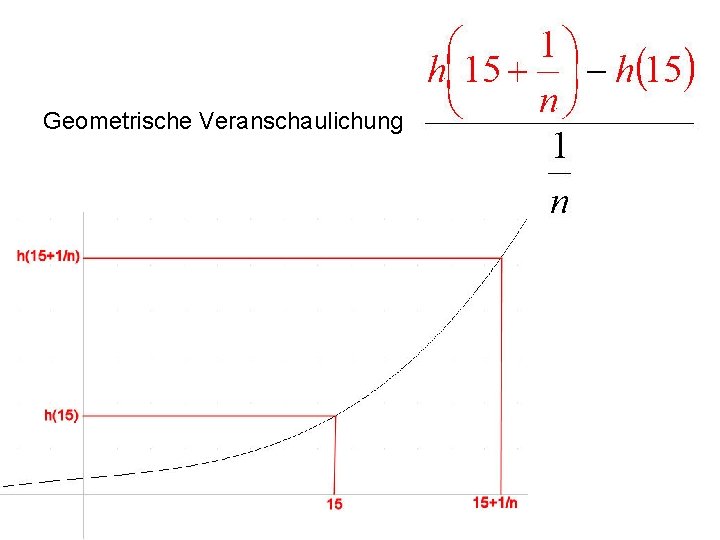
Geometrische Veranschaulichung

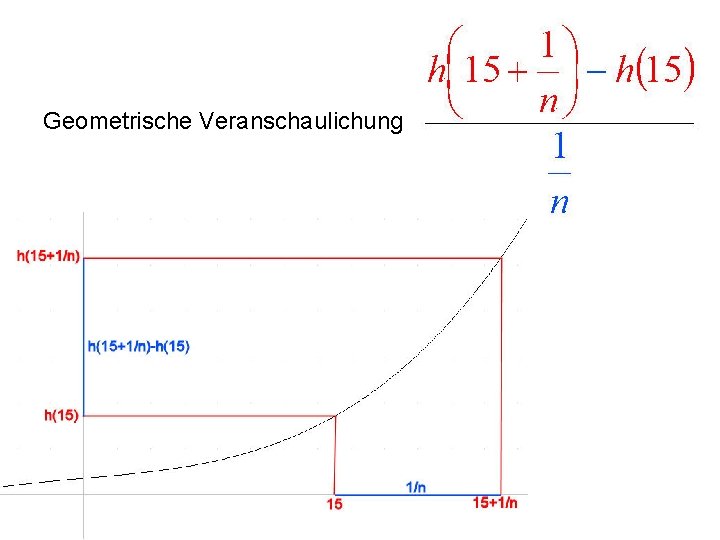
Geometrische Veranschaulichung

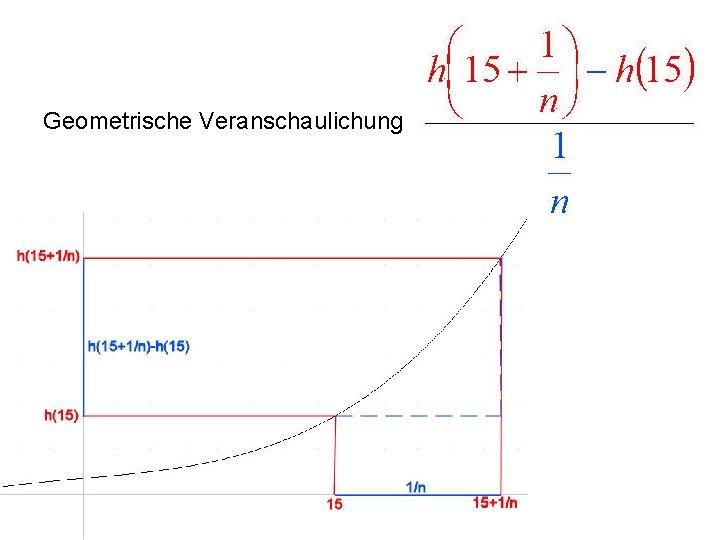
Geometrische Veranschaulichung

Geometrische Veranschaulichung

Geometrische Veranschaulichung

Beispielaufgabe Die Füllmenge in einem Vorratsbehälter ist gegeben durch die Funktion mit der Gleichung: Dabei ist V in m³ und t in Stunden gemessen. Betrachtet wird der Ablauf eines Tages, also t liegt zwischen 0 und 24.

a) Wie groß ist der Verbrauch im Laufe des Tages? b) Ist der Vorratsbehälter im Laufe des Tages irgendwann leer? c) Wann ist die Hälfte der Anfangsmenge im Behälter? d) Wie groß ist die durchschnittliche Verbrauchsrate während des Tages? e) Zu welchem Zeitpunkt ist die Verbrauchsrate maximal? f) Zu welchem Zeitpunkt ist der Verbrauchsrate minimal? g) Wie groß ist die minimale bzw. maximale Verbrauchsrate?

Bearbeiten Sie die Aufgabe zur Differentialrechung. Stellen Sie sich dabei auf den Kenntnisstand der Schüler ein. Noch nicht bekannt: Ableitungsregeln Ableitungsfunktion von CAS

Vergleich der Unterrichtsgänge zur Differentialrechnung Vorgehensweise ohne CAS Vorgehensweise mit CAS Motivierendes Einführungsbeispiel Kriterium: Einfache Berechenbarkeit Kriterium: interessanter Kontext Ableitungsregeln Anwendungen: neue Begriffe mit Hilfe der Ableitung Kriterien für Kurvendiskussion Ableitungsregeln werden an den Beispielen entdeckt Anwendungen: Kurvendiskussion und Extremwertaufgaben Kriterien als Hilfsmittel zum Aufstellen von Funktionsgleichungen

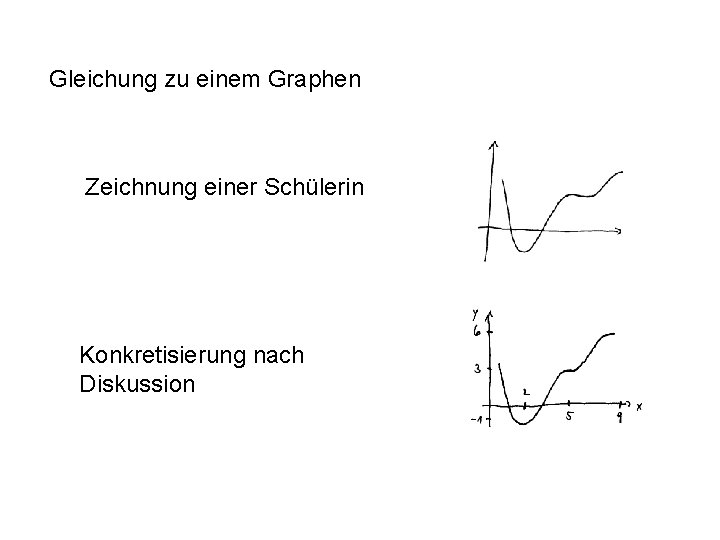
Gleichung zu einem Graphen Zeichnung einer Schülerin Konkretisierung nach Diskussion

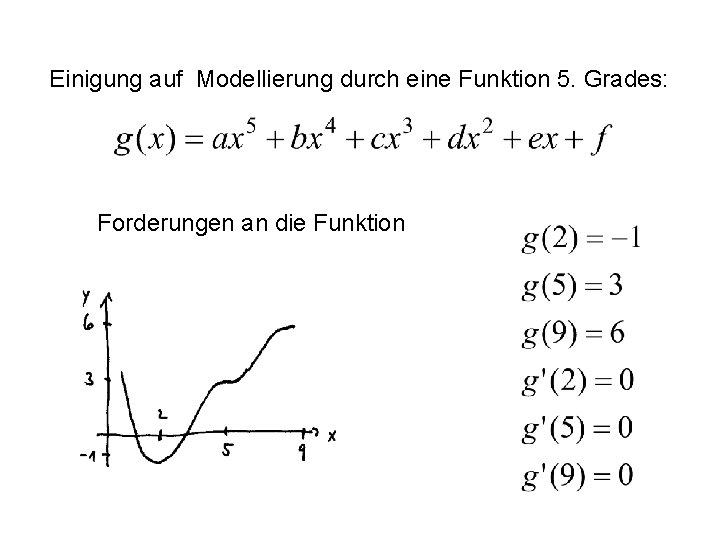
Einigung auf Modellierung durch eine Funktion 5. Grades: Forderungen an die Funktion

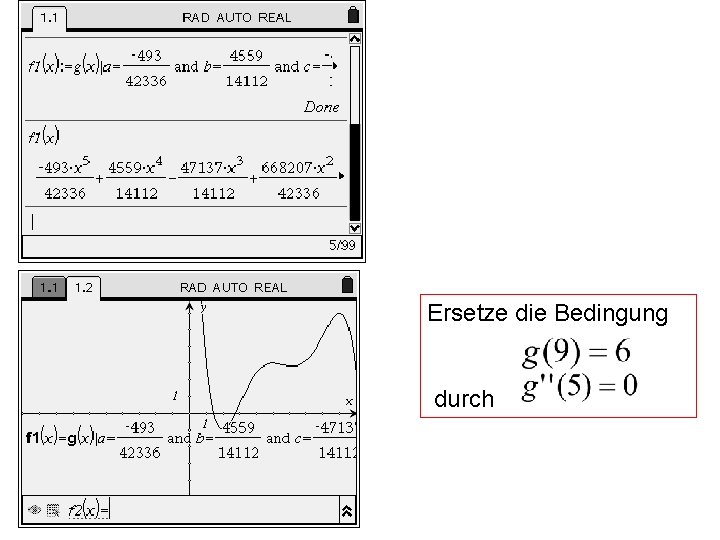
Ersetze die Bedingung durch

Umkehraufgaben zur Differentialrechnung Gegeben ist eine Volumenfunktion durch einen Term V(t). Schreiben Sie jeweils auf, zu welcher Fragestellung der Rechenansatz passt: a) b) c) d) e)

Einstiegsaufgabe Integralrechnung Aufgabenstellung: Bei einem Unfall in einer Fabrik wurden Schadstoffe freigesetzt. Die Menschen, die in der Umgebung lebten, wurden evakuiert. Es soll bestimmt werden, wie viel diese Menschen von den Schadstoffen bis zum Zeitpunkt der Evakuierung eingeatmet haben.

Menge Schadstoff in der Luft 500 l Konzentration d. Schadstoffs pro l Luft 2% / 20 ml Zeit bis zur Evakuierung 2 ½ Std Menge Luft die ein Mensch pro Stunde einatmet = 100 l Menge Schadstoffe " " " bis zur Evakuierung 5 l : 2 l

Menge Schadstoff in der Luft 500 l Konzentration d. Schadstoffs pro l Luft 2% / 20 ml Zeit bis zur Evakuierung 2 ½ Std Menge Luft die ein Mensch pro Stunde einatmet = 100 l Menge Schadstoffe " " " bis zur Evakuierung 5 l : 2 l

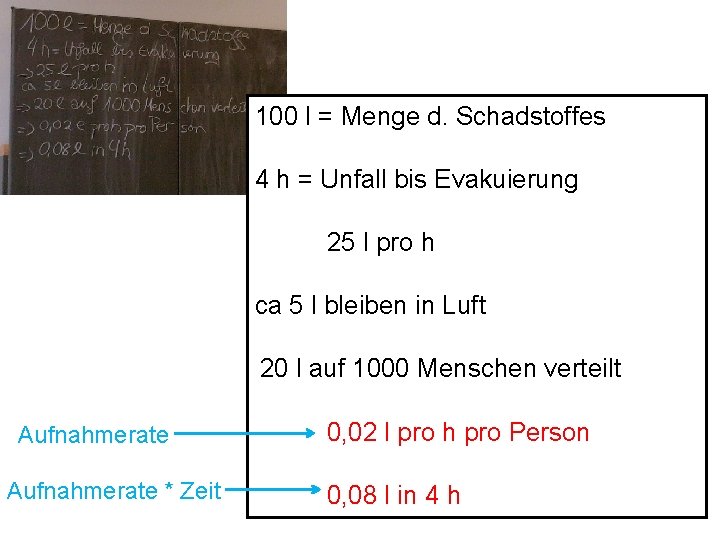
100 l = Menge d. Schadstoffes 4 h = Unfall bis Evakuierung 25 l pro h ca 5 l bleiben in Luft 20 l auf 1000 Menschen verteilt 0, 02 l pro h pro Person 0, 08 l in 4 h

100 l = Menge d. Schadstoffes 4 h = Unfall bis Evakuierung 25 l pro h ca 5 l bleiben in Luft 20 l auf 1000 Menschen verteilt Aufnahmerate * Zeit 0, 02 l pro h pro Person 0, 08 l in 4 h

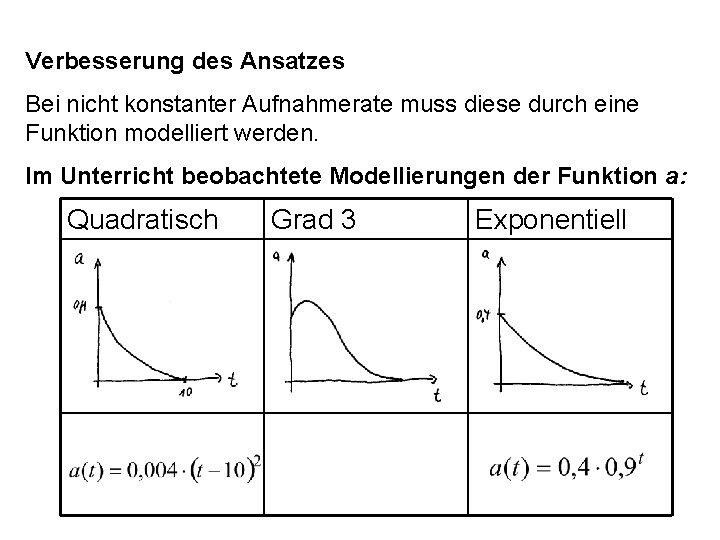
Verbesserung des Ansatzes Bei nicht konstanter Aufnahmerate muss diese durch eine Funktion modelliert werden. Im Unterricht beobachtete Modellierungen der Funktion a: Quadratisch Grad 3 Exponentiell

Problem: Wie multipliziert man eine Funktion mit der Zeitdauer? Grundidee: Teile die gesamte Zeitspanne in kurze Abschnitte ein und tue so, als wäre die Rate innerhalb eines Abschnittes konstant. Konkrete Ausführung: Evakuierung nach 4 Stunden. Teile in 8 Abschnitte. Wähle als konstanten Wert den Funktionswert jeweils am Anfang des Abschnittes:

Bisher im Unterricht beobachtete Ansätze Wähle als konstanten Wert Funktionswert am linken Rand des Abschnitts Funktionswert am rechten Rand des Abschnitts Funktionswert in der Mitte des Abschnitts Mittelwert der Funktionswerte an den Rändern

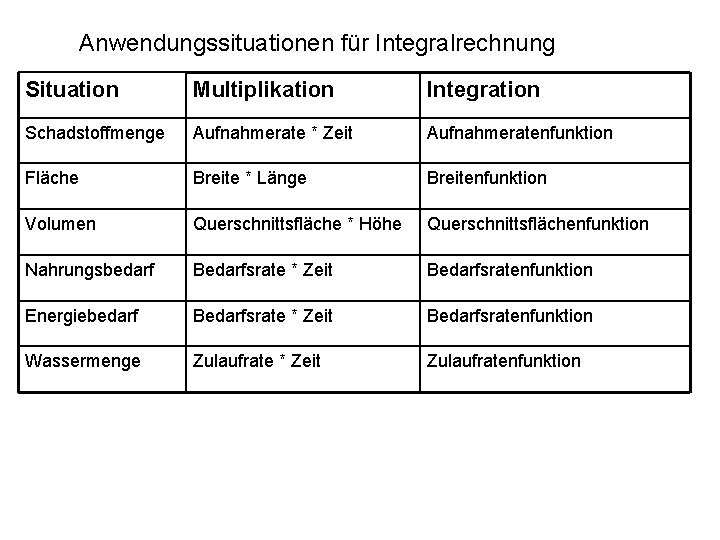
Anwendungssituationen für Integralrechnung Situation Multiplikation Integration Schadstoffmenge Aufnahmerate * Zeit Aufnahmeratenfunktion Fläche Breite * Länge Breitenfunktion Volumen Querschnittsfläche * Höhe Querschnittsflächenfunktion Nahrungsbedarf Bedarfsrate * Zeit Bedarfsratenfunktion Energiebedarf Bedarfsrate * Zeit Bedarfsratenfunktion Wassermenge Zulaufrate * Zeit Zulaufratenfunktion

Aufgabenbeispiel Gegeben ist die Zulaufratenfunktion für ein Wasserbecken durch im Intervall [0; 6]. Dabei ist t in Stunden in z in m³/h gemessen. Negative Werte der Zulaufratenfunktion bedeuten, dass Wasser abläuft. a) Bestimmen Sie die Zeitintervalle, in den Wasser zuläuft, und die Intervalle, in denen Wasser abläuft. b) Wie viel Wasser ist bis zum Ende der ersten Zulaufphase zugelaufen?

c) Zu welchem Zeitpunkt ist während der Ablaufphase der Anfangswasserstand wieder erreicht? d) Zu welchem Zeitpunkt ist das Becken am stärksten gefüllt? e) Zu welchem Zeitpunkt liegt die größte Zulaufrate vor? f) Zu welchem Zeitpunkt liegt die größte Ablaufrate vor? g) Zu welchem Zeitpunkt liegt die maximale Änderung der Zulaufrate vor? h) Nehmen Sie an, es würde sich bei der Funktion um eine Geschwindigkeitsfunktion handeln. Geben Sie zu jedem der Aufgabenteile a) bis g) an, was Sie dann ausgerechnet hätten.

Bearbeiten Sie die Aufgabe zur Integralrechnung. Stellen Sie sich dabei auf den Kenntnisstand der Schüler ein. Noch nicht bekannt: Integration mit Hilfe der Stammfunktionsmethode Integralfunktion von CAS Eventuell beschränken Sie sich auf die Teile zur Integralrechung

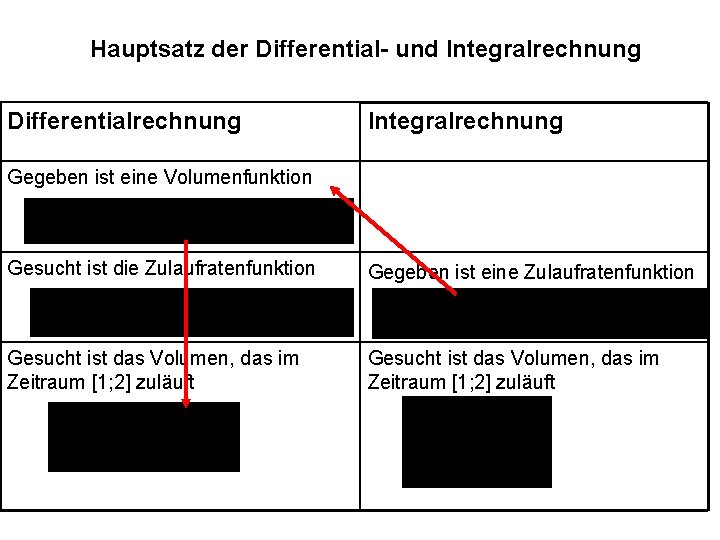
Hauptsatz der Differential- und Integralrechnung Differentialrechnung Gegeben ist eine Volumenfunktion Gesucht ist die Zulaufratenfunktion Integralrechnung

Hauptsatz der Differential- und Integralrechnung Differentialrechnung Integralrechnung Gegeben ist eine Volumenfunktion Gesucht ist die Zulaufratenfunktion Gegeben ist eine Zulaufratenfunktion Gesucht ist das Volumen, das im Zeitraum [1; 2] zuläuft

Hauptsatz der Differential- und Integralrechnung Differentialrechnung Integralrechnung Gegeben ist eine Volumenfunktion Gesucht ist die Zulaufratenfunktion Gegeben ist eine Zulaufratenfunktion Gesucht ist das Volumen, das im Zeitraum [1; 2] zuläuft

Abituraufgabe a) Zum Zeitpunkt 0 erfolgte die Einnahme eines Medikamentes. Gemessen wurde die Wirkstoffmenge in der Leber. Zu den Messpunkten wurde eine Ausgleichskurve mit der Gleichung gezeichnet. Im Graphen sind ein Hoch und ein Wendepunkt zu erkennen. Weisen Sie nach, dass es keine weiteren gibt.

b) Welche medizinische Bedeutung haben Extrema und Wendepunkte? c) Stellen Sie dar, in welchem Zeitraum das Modell der Ausgleichskurve sicherlich nicht mehr die Realität beschreibt. d) Für die medizinische Wirksamkeit eines Medikamentes kommt es neben der Menge des Wirkstoffes auch auf die Zeit an, in der Wirkstoff für den Körper zur Verfügung steht. Das Produkt aus Menge und Zeit wird ‚Wirksamkeit’ genannt. Erläutern Sie, wie die Wirksamkeit bestimmt wird, wenn die Menge des Wirkstoffes wie in diesem Fall durch eine Funktion gegeben ist, und berechnen Sie die Wirksamkeit für diese Funktion.

e) Für die Mediziner gilt das Medikament als abgebaut, wenn die Wirkstoffmenge unter der Nachweisgrenze von 0, 01 mg liegt. Von welchem Zeitpunkt an, kann das Medikament als abgebaut gelten? f) Die Gleichung in Teil e) lässt sich nicht algebraisch lösen. Stellen Sie als ein Beispiel eines nummerischen Verfahrens das Newtonverfahren dar und führen Sie die beiden ersten Schritte an der Gleichung aus Teil e) durch.

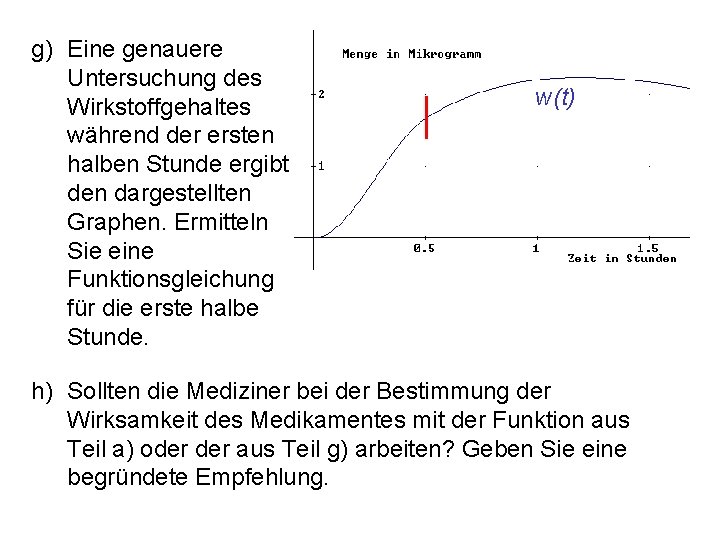
g) Eine genauere Untersuchung des Wirkstoffgehaltes während der ersten halben Stunde ergibt den dargestellten Graphen. Ermitteln Sie eine Funktionsgleichung für die erste halbe Stunde. w(t) h) Sollten die Mediziner bei der Bestimmung der Wirksamkeit des Medikamentes mit der Funktion aus Teil a) oder aus Teil g) arbeiten? Geben Sie eine begründete Empfehlung.

www. ruesing-essen. de