ACS 123 Functions Dr Viktor Fedun Automatic Control









![Example 1 (Page 136, Kuldeep and Singh, Example 3) [Mechanics] The displacement, φ(t), of Example 1 (Page 136, Kuldeep and Singh, Example 3) [Mechanics] The displacement, φ(t), of](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-10.jpg)








![Example 2 (Page 152 Kuldeep Singh, Example 16) [Reliability Engineering] The failure density function, Example 2 (Page 152 Kuldeep Singh, Example 16) [Reliability Engineering] The failure density function,](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-19.jpg)


![Example 3 (Page 110 Example 7) [Fluid Mechanics] The streamlines of fluid flow are Example 3 (Page 110 Example 7) [Fluid Mechanics] The streamlines of fluid flow are](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-22.jpg)







































![Example 1 (Page 251 Example 21) [Electrical Principles] A transmission line of length L Example 1 (Page 251 Example 21) [Electrical Principles] A transmission line of length L](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-70.jpg)

![Example 2 (Page 251 Example 22) [Electronics] In a semiconductor, a force, F, exerted Example 2 (Page 251 Example 22) [Electronics] In a semiconductor, a force, F, exerted](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-72.jpg)
![Show that F = Qck/2[1+cosh(kx)] Solution: so hence F = Qcke-kx/(1+e-kx)2 (*) F = Show that F = Qck/2[1+cosh(kx)] Solution: so hence F = Qcke-kx/(1+e-kx)2 (*) F =](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-73.jpg)






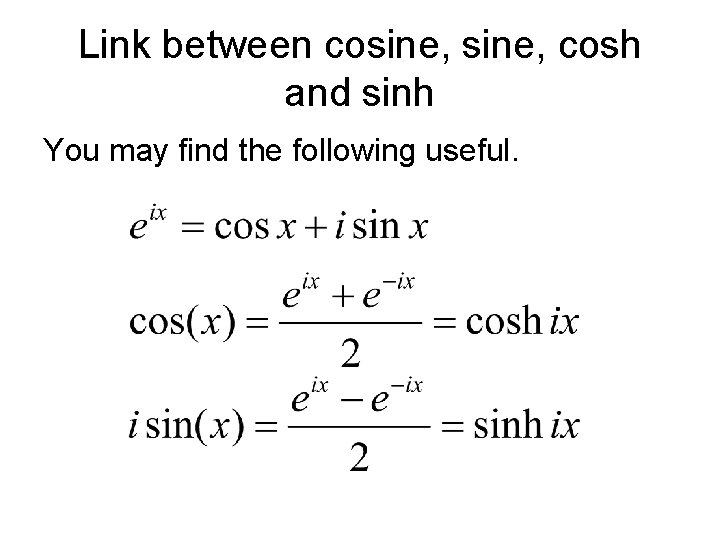
- Slides: 80

ACS 123 Functions Dr Viktor Fedun Automatic Control and Systems Engineering, C 09 Based on lectures by Dr Anthony Rossiter

Why is mathematics important? Why do engineers need to be good at mathematics? Is it sufficient to memorise key results? Just because a learning technique worked at school, does that make it the best method now? What mathematics do I need to be good at?

Mathematics is a tool-kit A good engineer: 1. knows which is the best tool to use? 2. Is proficient in using the tool? 3. Can adapt the tool to a new use. It is not good enough to memorise key results as the most important skill is abstraction. You must put your effort into understanding.

Module assessment • 3 in class tests in weeks 4, 7, 11, 13 These will be similar to exam questions. • An exam in May or June If you want feedback on an answer you have done, ask in a tutorial. 20 credit module, similar pattern in semester 2.

Module organisation I will teach the first semester Lectures and tutorials Of the 5 timetabled hours, 2 -3 will be used for lectures (these times may vary each week).

MOLE Please use the discussions board to ask questions. Then everyone can see the question and answer. I will not respond to email queries unless of a personal or private nature.

Resources Learning is only effective where students engage in self-discovery. 1. What you hear, you will usually forget. 2. You only really understand something when you use it. 3. We will provide ample materials, but YOU will only learn if you use these properly. [5 -6 hours per week] Lecturers are here to guide – NOT TO TEACH! We will answer queries and be as helpful as possible, but only you can do the work.

Be a function Stand up. 1. Use your arms to illustrate y=x. 2. What about y=-x? 3. Can you do y=x 2, or even x 3. 4. What about sine(x) – you may need a partner. Now do cosine(x). 5. Can you y=mod(x)? Or even y=sqrt(x 2)? 6. Can you think of any more?

Common functions 1. 2. 3. 4. sine, cosine, tangent (and their inverses) logarithm, exponential sinh and cosh straightline, quadratic, general polynomial 5. combinations of above as products, composites and fractions. You should be familiar with shapes of common functions and be able to sketch quickly.
![Example 1 Page 136 Kuldeep and Singh Example 3 Mechanics The displacement φt of Example 1 (Page 136, Kuldeep and Singh, Example 3) [Mechanics] The displacement, φ(t), of](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-10.jpg)
Example 1 (Page 136, Kuldeep and Singh, Example 3) [Mechanics] The displacement, φ(t), of a particle at time t is given by: φ(t)= 2 t 3 + t 2 - 10 t + 10 (a) Evaluate φ(2), φ(3), φ(5). (b) Find simplified expressions for: (i) φ(t 2) (ii) φ(t + 1)

Example 1 Solution: (a) We have (a) φ(2) = (2 x 23) + 22 – (10 x 2) + 10 = 10 (a) φ(3) = (2 x 33) + 32 – (10 x 3) + 10 = 43 (b) φ(5) = (2 x 53) + 52 – (10 x 5) + 10 = 235

Example 1 Solution (b) (i) For φ(t 2) we replace the t with t 2 in φ(t)= 2 t 3 + t 2 - 10 t + 10: φ(t 2) = 2(t 2)3 + (t 2)2 – 10(t 2) + 10 = 2 t 6 + t 4 – 10 t 2 + 10 (ii) For φ(t + 1) we replace t with t+1 in φ(t)= 2 t 3 + t 2 - 10 t + 10: φ(t+1)= 2(t+1)3 + (t+1)2 – 10(t+1) + 10:

What is a function? 1. A rule which translates an input, usually to a single output. 2. What are the functions for: i. Double the input ii. Shift the input by 3 iii. Cube the input and subtract 1. 3. Write down in words the functions for

What variables can a function have? What is the difference between the functions f(x), g(w), h(y) and k(x) A function describes a relationship, the variable names are unimportant. Engineers typically use variable names that relate to the topic: W for weight, h for height, L for length, etc.

What is a function argument? The part that appears in the brackets; • For y=f(x), x is the argument. • For z=g(w), w is the argument. Thus argument is another word for the input to the function. Independent and dependent variables: what do you think these are? Use common sense.

Composition of functions What do the following statements mean?

Evaluate the following Find y when x=pi/2. Find w when z=1.

Function products Evaluate A given that: A = y 2 h with x=2 and z=3 Write down a detailed function expression to express A.
![Example 2 Page 152 Kuldeep Singh Example 16 Reliability Engineering The failure density function Example 2 (Page 152 Kuldeep Singh, Example 16) [Reliability Engineering] The failure density function,](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-19.jpg)
Example 2 (Page 152 Kuldeep Singh, Example 16) [Reliability Engineering] The failure density function, f(t), for a component is given by: f(t) = 1/8 where 0 < t < 8 years. Find F(t), R(t) and h(t) where these are defined as: F(t) = tf(t) (Failure Distribution function) R(t) = 1 -F(t) (Reliability function) h(t) = f(t) / R(t) (hazard Rate function) and 0 < t < 8 years.

Example 2 (Page 152 Example 16) Solution We have: F(t) = tf(t) = t(1/8) = t/8. R(t) = 1 -F(t) = 1 - t/8 h(t) = f(t) / R(t) = (1/8)/(1 -t/8) = 1/(8 -t)

Graphs and sketching By first producing a suitable, sketch the graphs of the following functions in the domain -3 to 3. Domain is the values allowed to the argument or independent variable. Range is the values the output (dependent variable) can take. What is the range of these?
![Example 3 Page 110 Example 7 Fluid Mechanics The streamlines of fluid flow are Example 3 (Page 110 Example 7) [Fluid Mechanics] The streamlines of fluid flow are](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-22.jpg)
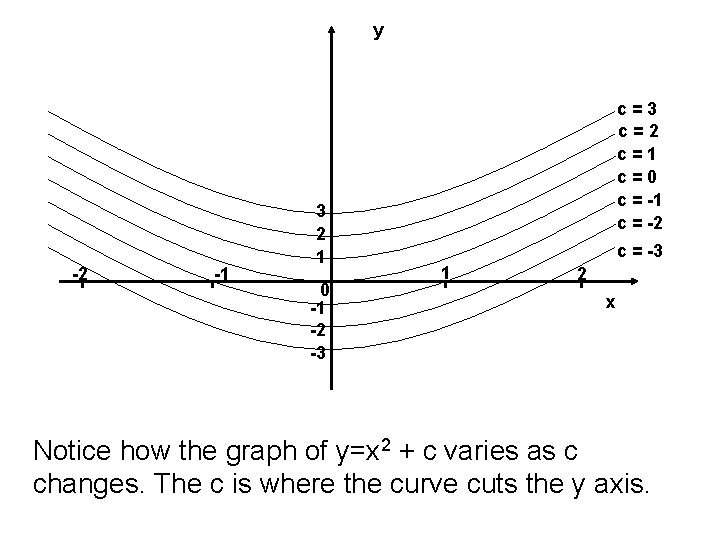
Example 3 (Page 110 Example 7) [Fluid Mechanics] The streamlines of fluid flow are given by: y = x 2 + c where c is constant. Sketch the streamlines for c = 0, -1 , 1, -2, 2, -3 and 3.

Example 3 (Page 110 Example 7) Solution The graphs of y = x 2 + c for c = 0, -1 , 1, -2, 2, -3 and 3 are: (c=0) y = x 2 (c=-1) y = x 2 - 1 (c=1) y = x 2 + 1 (c=-2) y = x 2 -2 (c=2) y = x 2 +2 (c=-3) y = x 2 – 3 (c=3) y = x 2 + 3

y -2 -1 3 2 1 0 -1 -2 -3 c=2 c=1 c=0 c = -1 c = -2 c = -3 1 2 x Notice how the graph of y=x 2 + c varies as c changes. The c is where the curve cuts the y axis.

Inverse function mean that all we’ve done is made a switch in emphasis

Inverse function mean that all we’ve done is made a switch in emphasis 7– 4=3 3+4=7

Inverse function mean that all we’ve done is made a switch in emphasis 7– 4=3 3+4=7 Both of this statements say the same thing, but with a change in emphasis

Inverse function mean that all we’ve done is made a switch in emphasis 7– 4=3 3+4=7 Both of this statements say the same thing, but with a change in emphasis

Inverse function mean that all we’ve done is made a switch in emphasis 7– 4=3 3+4=7 Both of this statements say the same thing, but with a change in emphasis -1

Inverse function example y=2 x-7; y=f(x)=2 x-7

Inverse function example y=2 x-7; y=f(x)=2 x-7 Identity function

Inverse function example y=2 x-7; y=f(x)=2 x-7 Identity function If and inverse function

Inverse function example y=2 x-7; y=f(x)=2 x-7 Identity function If and inverse function Composition of functions

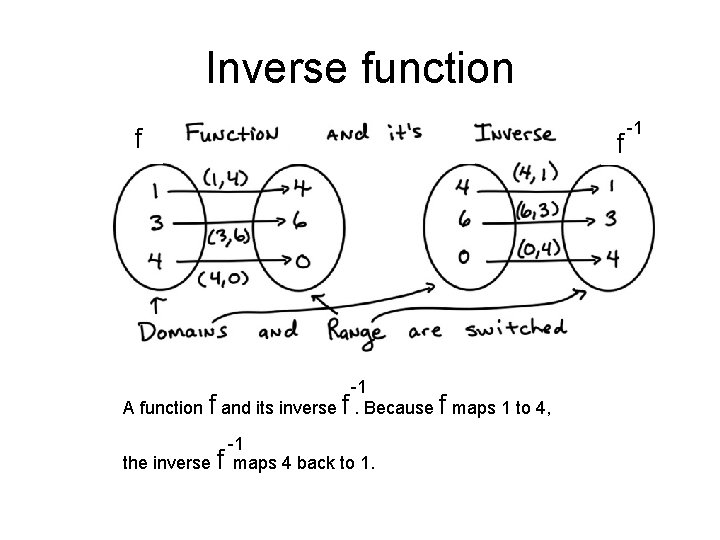
Inverse function f -1 A function f and its inverse f . Because f maps 1 to 4, -1 the inverse f maps 4 back to 1. f -1

One to one function For every value of x, there is a distinct value of y and for every value of y there is a distinct value of x. Which of the following is one to one? Draw the graph and it should be obvious.

Inverse function Proof What about?

Inverse function example

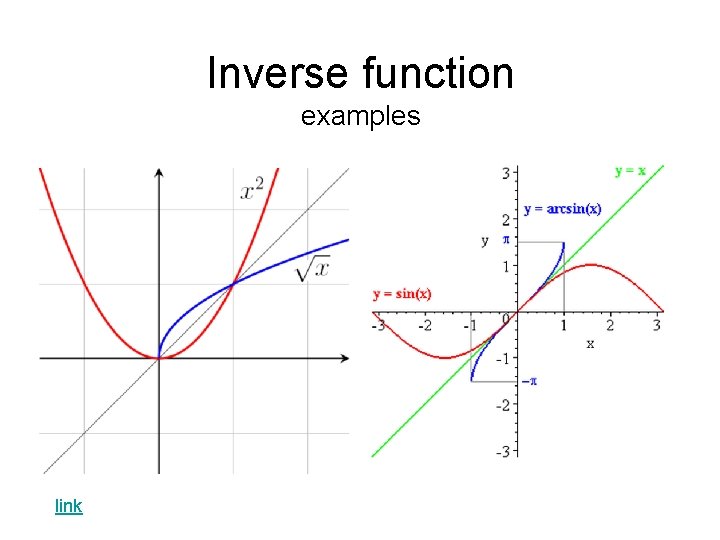
Inverse function example Sometimes the inverse of a function cannot be expressed by a formula with a finite number of terms. For example, if f is the function -1 then f is one-to-one, and therefore possesses an inverse function f . The formula for this inverse has an infinite number of terms:

Inverse function examples link

Many-to-one and one-to-many Give some examples of many-to-one and one-to-many functions. The logic goes from independent variable to dependent variable.

Notation Get into groups and decide three example functions with the following properties [3 for each item]. 1. Continuous 2. Discontinuous 3. Periodic (Why are these important? ) 4. Odd 5. Even


Odd Even

Summary Independent variable (domain) Dependent variable (range) Function Many-to-one (one-to-one, …) Odd, even, periodic Inverse function Continuous/discontinuous Composite function Straight lines

Exponential functions On some rough paper, do a sketch of the following functions. In what sense are the functions equivalent? With a suitable rescaling of x, they are all the same shape. Functions of this form are called exponentials.


Exponential properties If you double the value of the independent variable, you square the value of the dependent variable. There is a constant ratio which depends solely on the difference of the argument: For all x!

Exponential properties

Exponential properties Exponentiation is not commutative 4+5=5+4 4*5=5*4 but 4 256 5 = 4 625

Exponential properties Exponentiation is not commutative 4+5=5+4 4*5=5*4 Exponentiation is not associative (2 + 3) + 4 = 2 + (3 + 4) but 3 4 (2 ) = 4096 but 4 5 256 = 5 = 4 625 (2 * 3) * 4 = 2 * (3 * 4) ( 34) 2 = 2. 417. 851. 639. 229. 258. 349. 412. 353

Exponential convention 1. When dealing with exponential functions it is usual to assume the same base – ALWAYS! 2. The assumed base is `e’. 3. It will become clearer later why `e’ is chosen because this makes a lot of common algebra much simpler. 4. `e’ is irrational, but has a value near 2. 7

Exponential convention 1. When dealing with exponential functions it is usual to assume the same base – ALWAYS! 2. The assumed base is `e’. 3. It will become clearer later why `e’ is chosen because this makes a lot of common algebra much simpler. 4. `e’ is irrational, but has a value near 2. 7 and more precisely

Common exponential The most common functions you will deal with are: A positive exponent gives an increasing function with increasing argument. A negative exponent gives a decreasing argument with exponent.


Exponentials and systems engineering The behaviour of real systems is often described as an exponential decay. 1. Radioactivity follows a curve of the form. 2. An explosion might be an increasing function. 3. Many systems have dynamics with 2 exponentials. If behaviour has a positive exponent – BEWARE!

Note Logarithms and exponentials are inverse functions of one another.

Even/odd and hyperbolic Functions

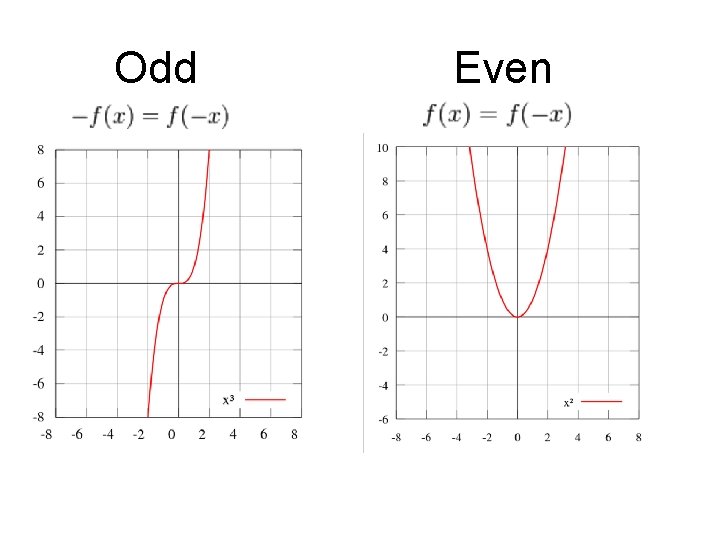
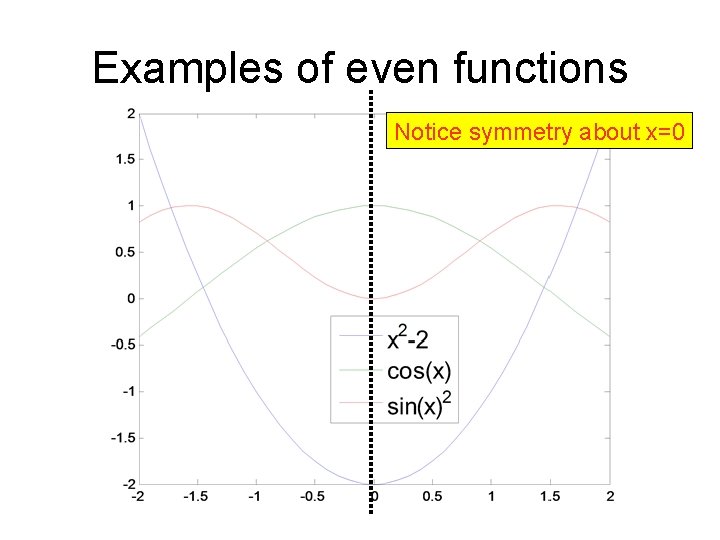
Even functions An even function is one whereby the vertical axis is equivalent to a mirror. In mathematical terms, this means that f(-x)=f(x)

Examples of even functions Notice symmetry about x=0

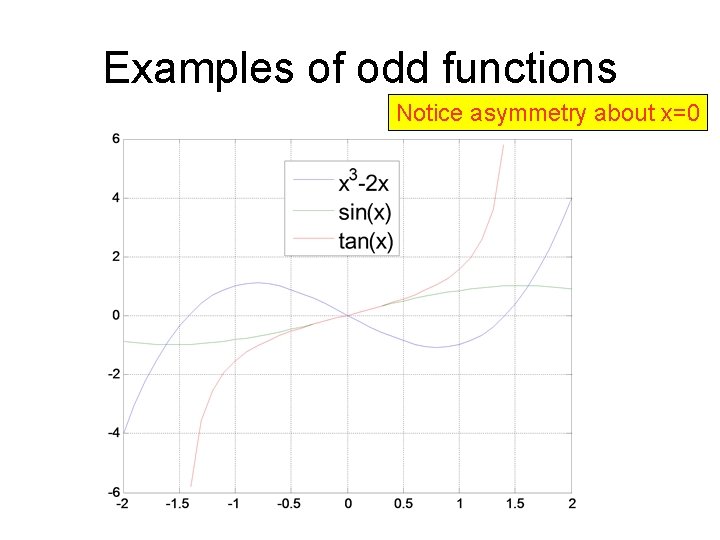
Odd functions An odd function is one whereby the vertical axis reverses the value of the function. In mathematical terms, this means that f(-x)=-f(x)

Examples of odd functions Notice asymmetry about x=0

Constructing even and odd functions Every function can be made up of even and odd functions. This can make some engineering problems easier to handle. EVEN FUNCTIONS ODD FUNCTIONS f(x)=f(-x) f(x)=-f(-x)

Constructing even and odd functions EVEN ODD EVEN FUNCTIONS ODD FUNCTIONS f(x)=f(-x) f(x)=-f(-x)

Construct even and odd functions to make up the following

Construct even and odd functions to make up the following USE

Simple rules • • • EVEN*EVEN = EVEN ODD*ODD = EVEN*ODD=ODD EVEN+EVEN=EVEN ODD+ODD=ODD ODD+EVEN=NEITHER ODD NOR EVEN Can you prove these?

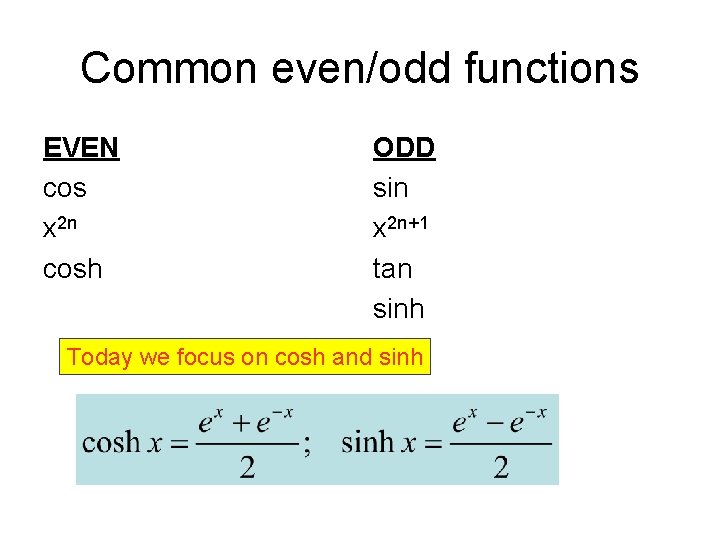
Common even/odd functions EVEN cos x 2 n cosh ODD sin x 2 n+1 tan sinh Today we focus on cosh and sinh

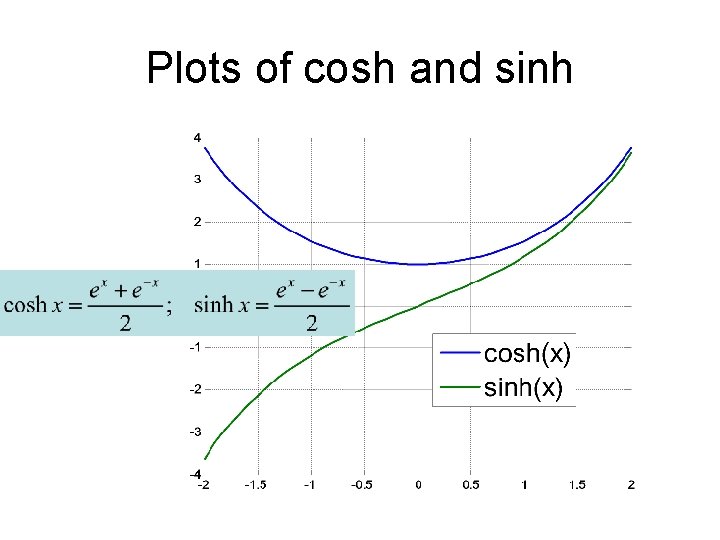
Plots of cosh and sinh

Engineering examples of cosh and sinh • Some examples taken from the following book: – “Engineering Mathematics through Applications” • Kuldeep Singh – Published by: Palgrave Mac. Millan – ISBN 0 -333 -92224 -7
![Example 1 Page 251 Example 21 Electrical Principles A transmission line of length L Example 1 (Page 251 Example 21) [Electrical Principles] A transmission line of length L](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-70.jpg)
Example 1 (Page 251 Example 21) [Electrical Principles] A transmission line of length L has voltage V. At a distance x from the sending end, the voltage is given by: VL = ½(V + IZ 0)e-φx + ½(V - IZ 0)eφx (*) Where I is the current, Z 0 is the characteristic impedance and φ is the propagation coefficient.

Show that at x = L: VL = Vcosh(φL) - IZ 0 sinh(φL) VL = ½(V + IZ 0)e-φx + ½(V - IZ 0)eφx (*) Solution: Putting x = L into (*) gives: VL = ½(V + IZ 0)e-φL + ½(V - IZ 0)eφL = V(e-φL + eφL)/2 + IZ 0(e-φL - eφL)/2 = Vcosh(φL) + IZ 0(e-φL - eφL)/2 so VL = Vcosh(φL) + IZ 0 sinh(φL)
![Example 2 Page 251 Example 22 Electronics In a semiconductor a force F exerted Example 2 (Page 251 Example 22) [Electronics] In a semiconductor, a force, F, exerted](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-72.jpg)
Example 2 (Page 251 Example 22) [Electronics] In a semiconductor, a force, F, exerted on an electron is given by: F = Qcke-kx/(1+e-kx)2 (*) Where c and k are constants, x is the distance from the pn junction and Q is the charge. Show that F = Qck/2[1+cosh(kx)]
![Show that F Qck21coshkx Solution so hence F Qckekx1ekx2 F Show that F = Qck/2[1+cosh(kx)] Solution: so hence F = Qcke-kx/(1+e-kx)2 (*) F =](https://slidetodoc.com/presentation_image_h/874f495052931a02b854b818c0491b24/image-73.jpg)
Show that F = Qck/2[1+cosh(kx)] Solution: so hence F = Qcke-kx/(1+e-kx)2 (*) F = Qcke-kx/(1 + 2 e-kx + e-2 kx) = Qcke-kx / e-kx (ekx + 2 + e-kx) = Qck /(2 + ekx + e-kx) = Qck /(2 + 2(ekx + e-kx)/2) = Qck /(2 + 2 cosh(kx)) F = Qck/2[1+cosh(kx)]

Solution to ODES Where an ODE takes the form The solution can be represented in two similar ways.

Identities You should be familiar with common identities using cosh and sinh. Prove the following:

Use of hyperbolic equations with parametric descriptions Some simple curves lend themselves to parametric descriptions. Consider: 1. Circle 2. Ellipse 3. Hyperbola


Parametric descriptions the sine and cosine functions give a parametric equation for the ellipse the hyperbolic sine and hyperbolic cosine give a parametric equation for the hyperbola ENGINEERING APPLICATION: Space orbits can be either elliptical or hyperbolic (often called a sling shot).

Questions 1. Simplify the following expressions. 2. Find parametric expressions for x, y satisfying the following hyperbola.
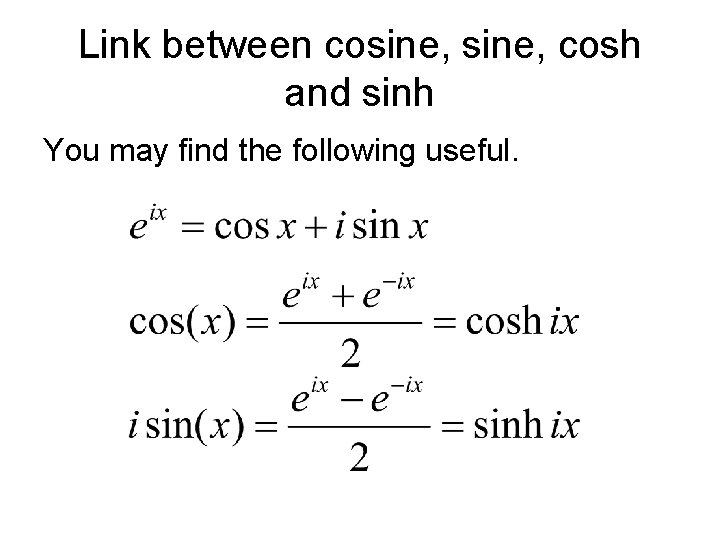
Link between cosine, cosh and sinh You may find the following useful.