AC Circuit Analysis Sinusoidal SteadyState Analysis Contents CHAPTER

AC Circuit Analysis Sinusoidal Steady-State Analysis

Contents (CHAPTER 10) Application of methods and theorem circuit to analyse the AC circuit eg • Nodal Analysis • Mesh Analysis • Superposition Theorem • Source Transformation • Thevenin and Norton Equivalent Circuits

Step to Analyze AC Circuits: 1. Transform the circuit to the phasor or frequency domain. 2. Solve the problem using method analysis or theorem circuit techniques. 3. Transform the resulting phasor to the time domain.

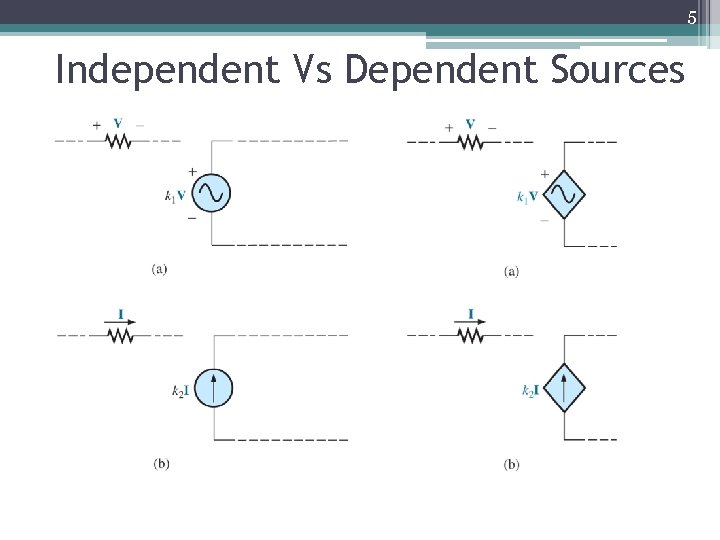
4 Independent Vs Dependent Sources • Independent sources: - The magnitude of the source is independent of the network to which it is applied & that the source displays its terminal characteristic even if completely isolated

5 Independent Vs Dependent Sources

6 Independent Vs Dependent Sources • Dependent/Controlled Sources: - One whose magnitude is determined (or controlled) by a current or voltage of the system in which it appears

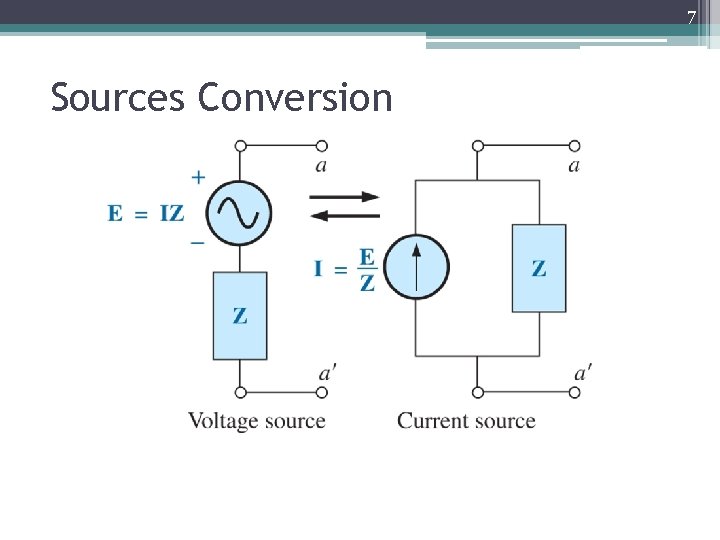
7 Sources Conversion

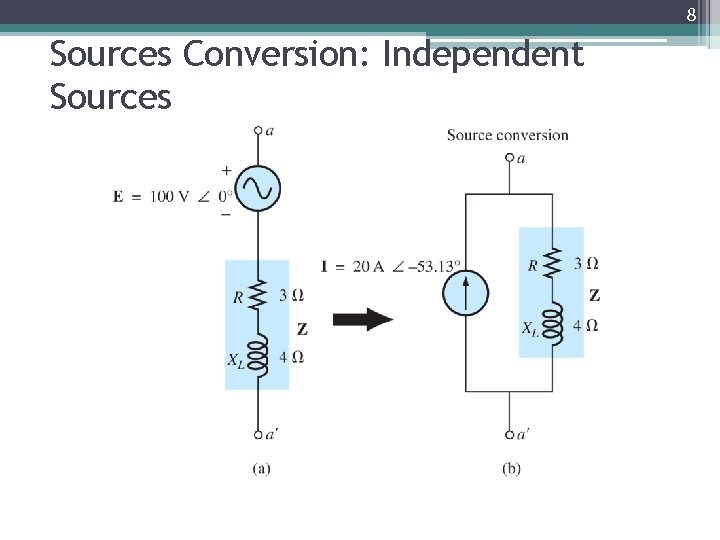
8 Sources Conversion: Independent Sources

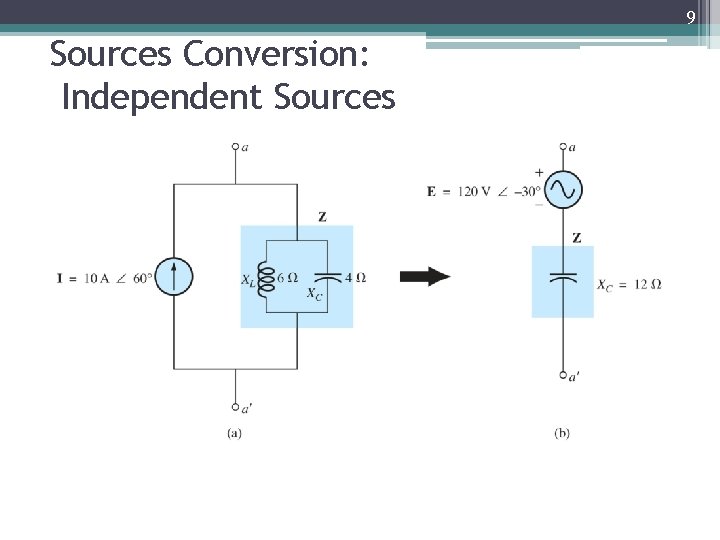
9 Sources Conversion: Independent Sources

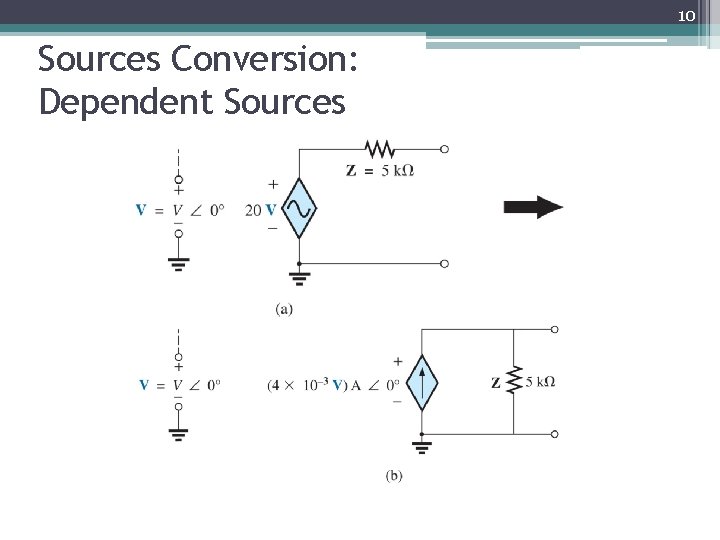
10 Sources Conversion: Dependent Sources

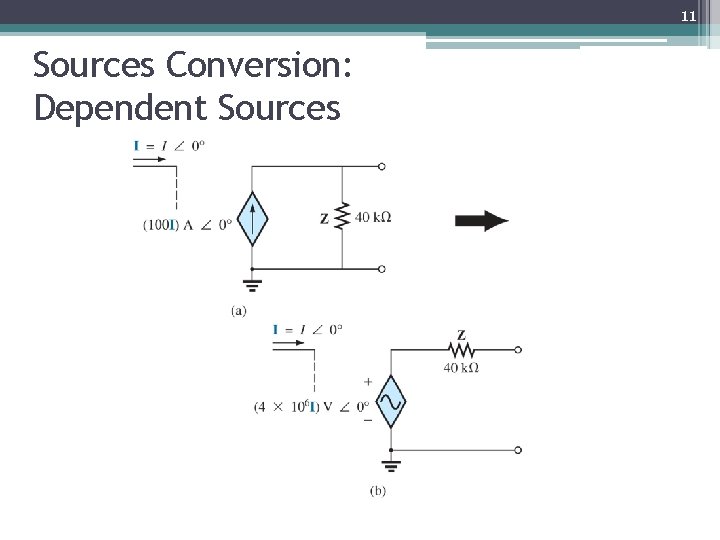
11 Sources Conversion: Dependent Sources

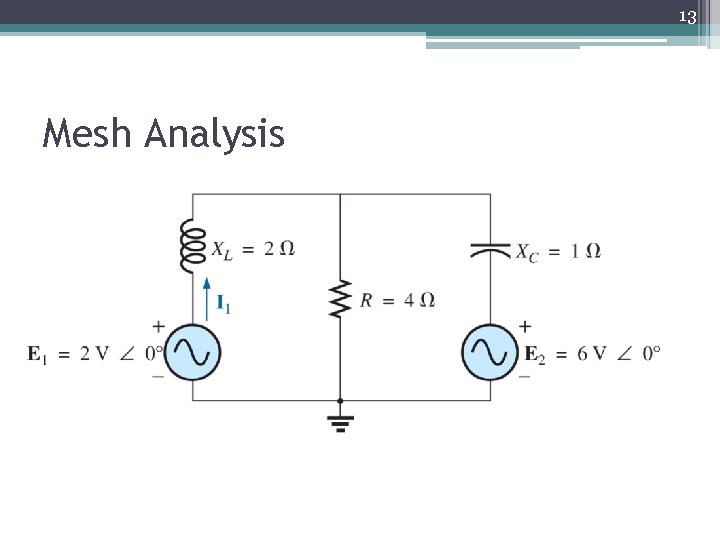
Mesh Analysis Steps in determining mesh current for circuit contain with only independent voltage source: 1. Assign mesh currents i 1, i 2, …in to the n meshes Assign mesh current in the clockwise direction around each non redundant closed loop 2. Apply KVL to each of the n meshes. Use Ohm’s Law to express the voltages in terms of the mesh currents. 3. Solve the resulting n simultaneously equations to get the mesh currents by using substitution or determinants.

13 Mesh Analysis

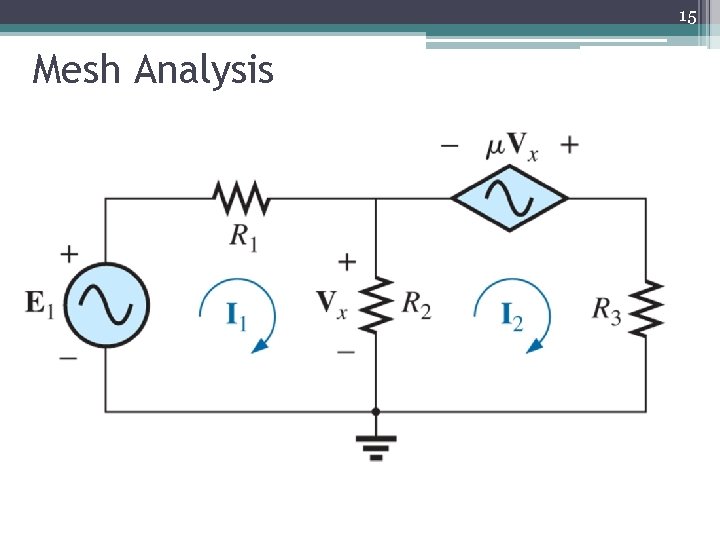
14 Mesh Analysis The step if circuit contain with dependent voltage sources • Step 1 & 2 are the same as those applied for independent sources • Treat each dependent source like an independent source when Kirchhoff’s voltage law is applied to each independent loop. Once the eq. ready, substitute the eq. for the controlling quantity to ensure that the unknown are limited solely to the chosen mesh currents • Solve the resulting simultaneous linear equations

15 Mesh Analysis

16 Mesh Analysis The step if circuit contain with independent current sources • Step 1 & 2 are the same as those applied for independent sources • Treat each current source as an open circuit (recall the supermesh) & write the mesh eq. for each remaining independent path. Then relate the chosen mesh current to the dependent sources to ensure that the unknown of the final eq. are limited to the mesh currents • Solve the resulting simultaneous linear equations

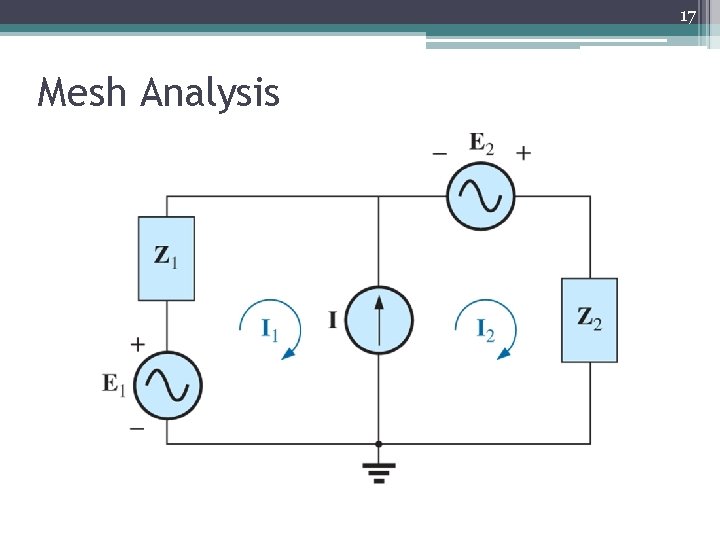
17 Mesh Analysis

18 Mesh Analysis The step if circuit contain with dependent current sources • Step 1 & 2 are the same as those applied for independent sources • The procedure is essentially the same as that applied for independent current sources, except now the dependent sources have to be defined in term of the chosen mesh currents to ensure that the final eq. have only mesh current as the unknown quantities • Solve the resulting simultaneous linear equations

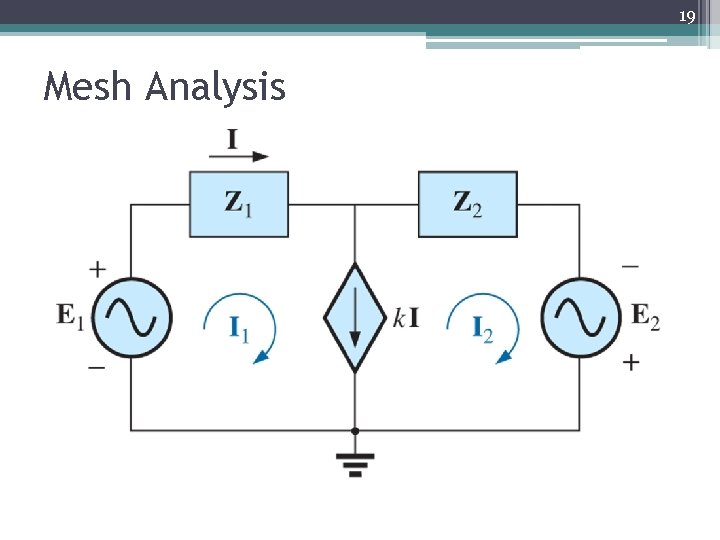
19 Mesh Analysis

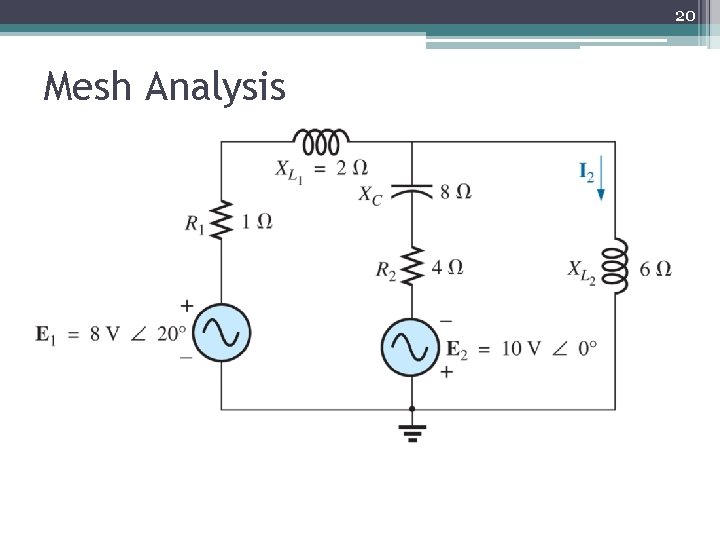
20 Mesh Analysis

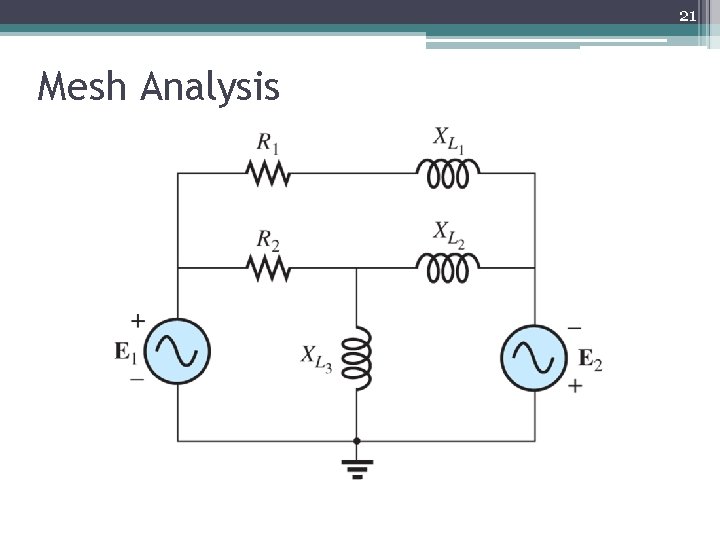
21 Mesh Analysis

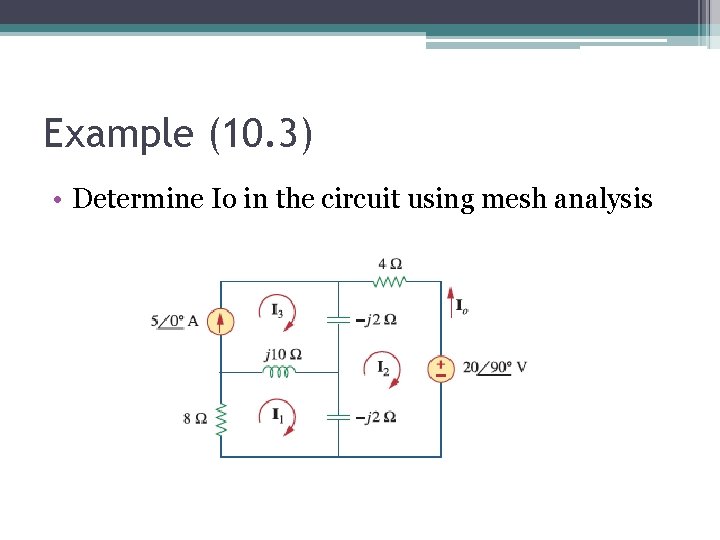
Example (10. 3) • Determine Io in the circuit using mesh analysis

Method Analysis • Nodal analysis 1. Steps to determine node voltage: i. Select reference node. ii. Assign voltage respect to reference node) iii. Apply KCL to each nonreference nodes. Use Ohm’s Law to express the branch currents. iv. Solve the resulting simultaneously equations to solve for node voltage to the remaining n-1 nodes (with

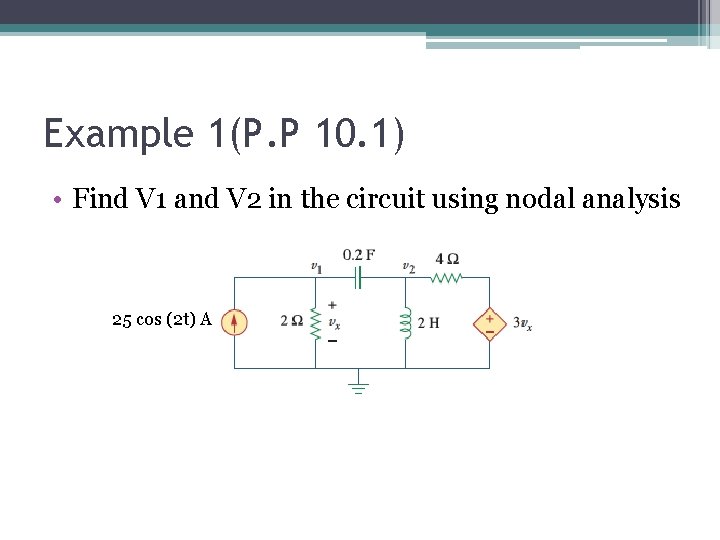
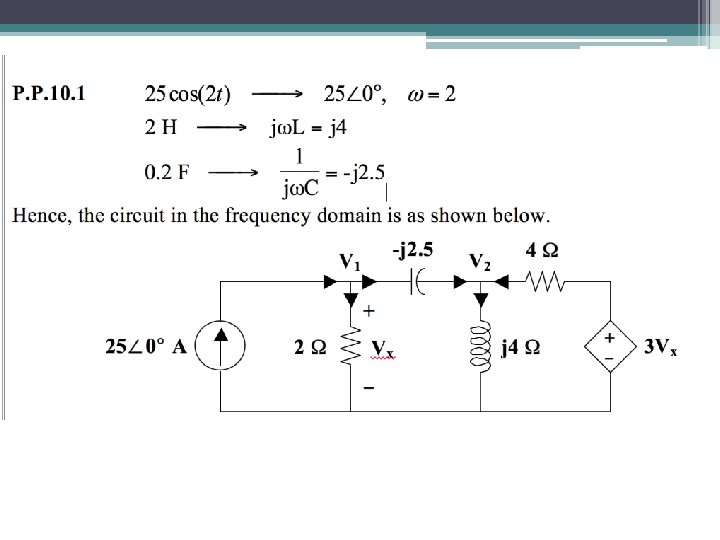
Example 1(P. P 10. 1) • Find V 1 and V 2 in the circuit using nodal analysis 25 cos (2 t) A

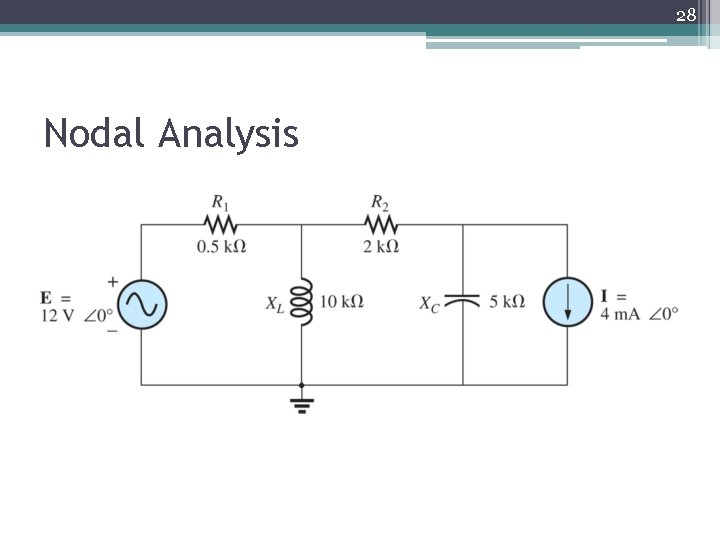
28 Nodal Analysis

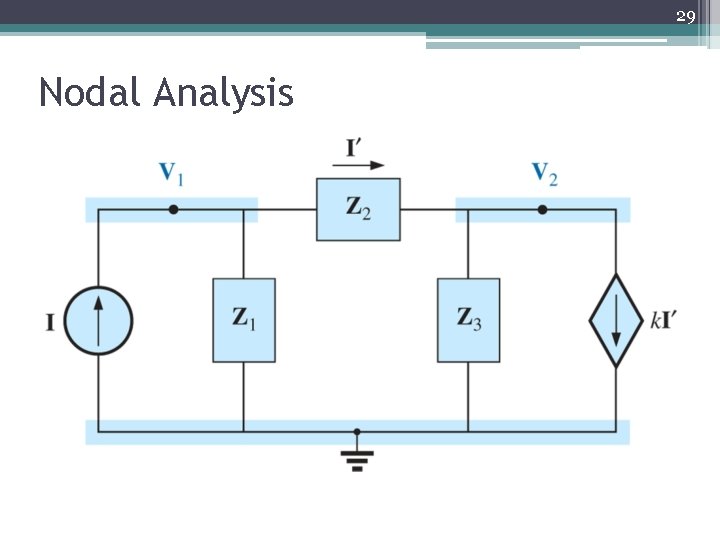
29 Nodal Analysis

30 Network Theorems (AC)

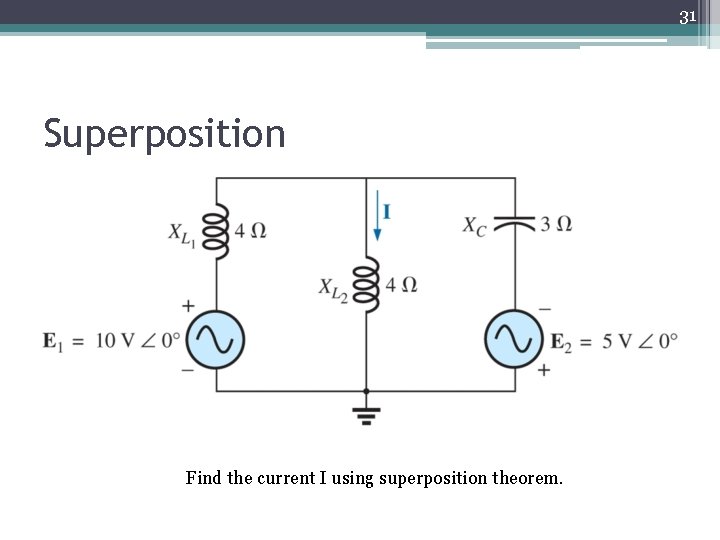
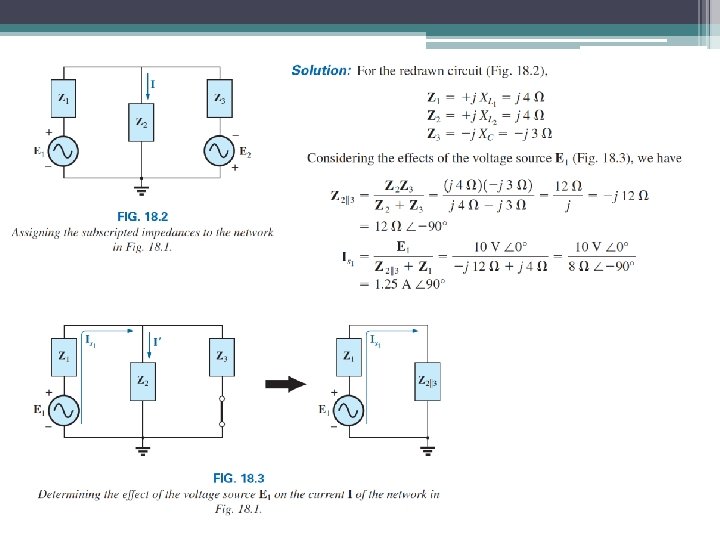
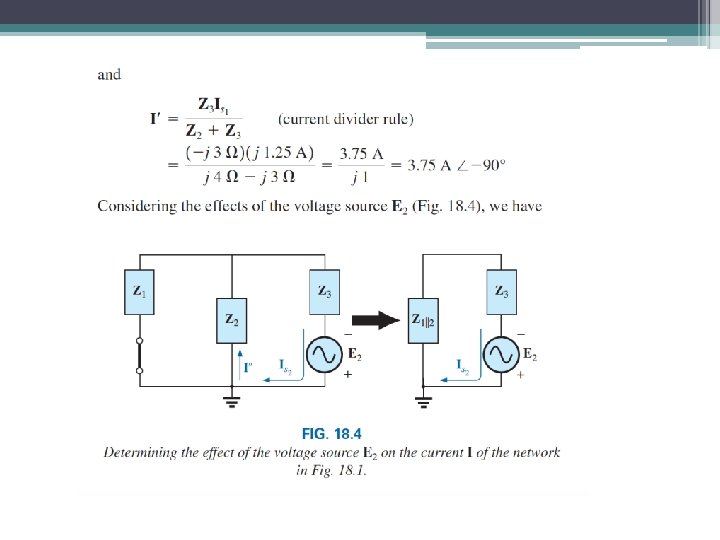
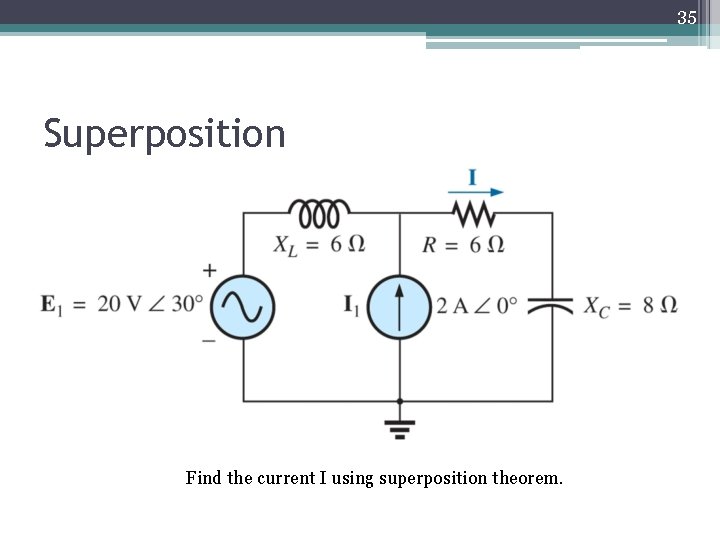
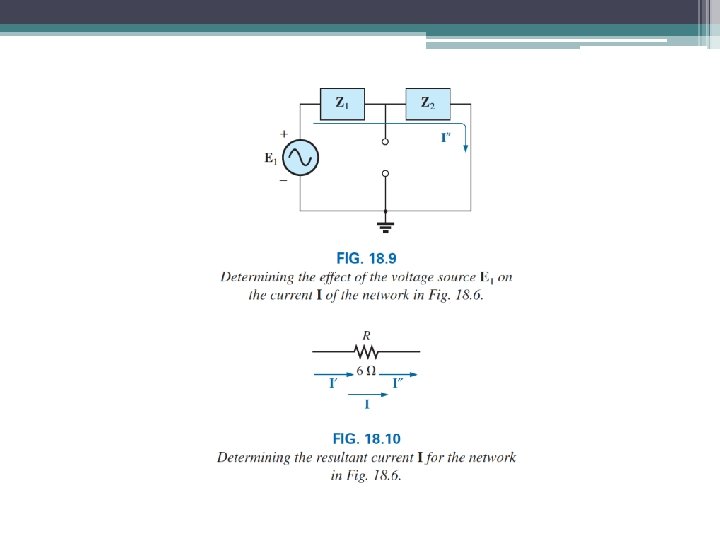
31 Superposition Find the current I using superposition theorem.

35 Superposition Find the current I using superposition theorem.

Thevenin and Norton Equivalent Circuit • Thevenin and Norton theorem applied to ac circuit in the same way as they are to dc circuit. Thevenin’s theorem states that a linear two – terminal circuit can be replaced by an equivalent circuit consisting of a voltage source VTH in series with a resistor ZTH, where VTH is the open circuit voltage at the terminals and RTH is the input or equivalent resistance at the terminals when the independent sources are turned off.

Norton’s theorem states that a linear two-terminal circuit can be replaced by an equivalent circuit consisting of a current source IN in parallel with a resistor ZN where IN is the short circuit current between two output terminals in the circuit and ZN is the total equivalent resistance at the terminals when the independent sources are turned off.

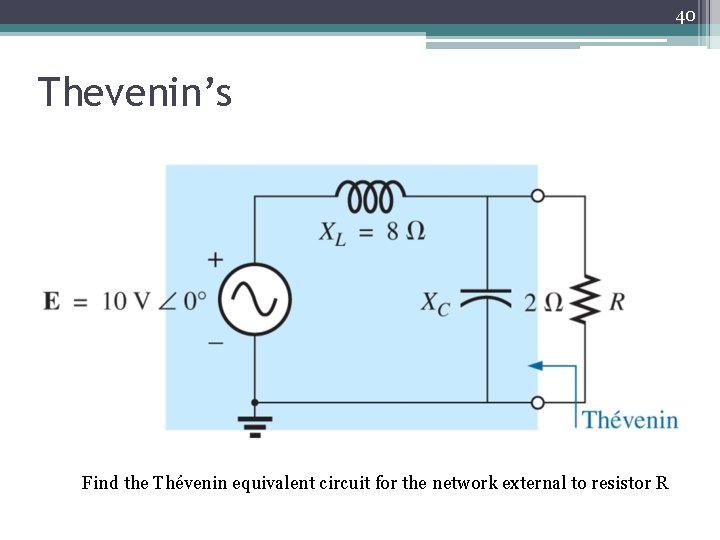
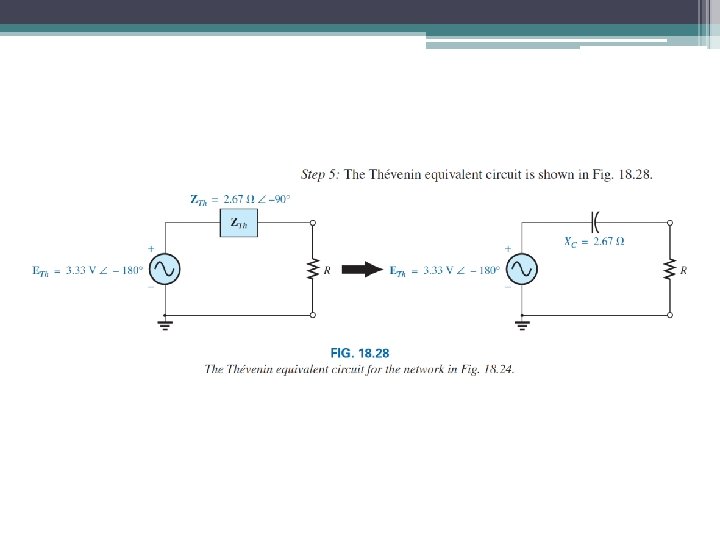
40 Thevenin’s Find the Thévenin equivalent circuit for the network external to resistor R

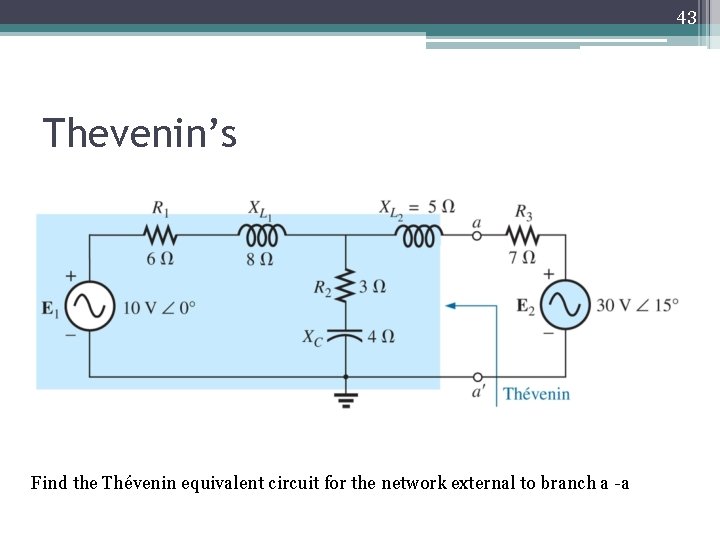
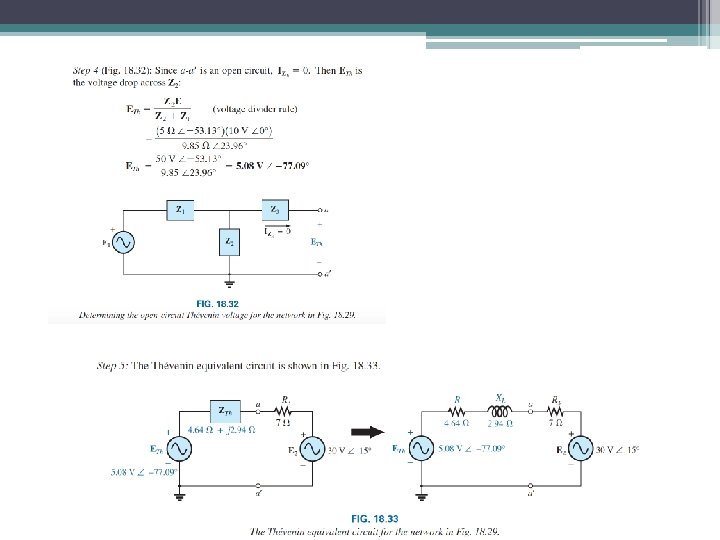
43 Thevenin’s Find the Thévenin equivalent circuit for the network external to branch a -a

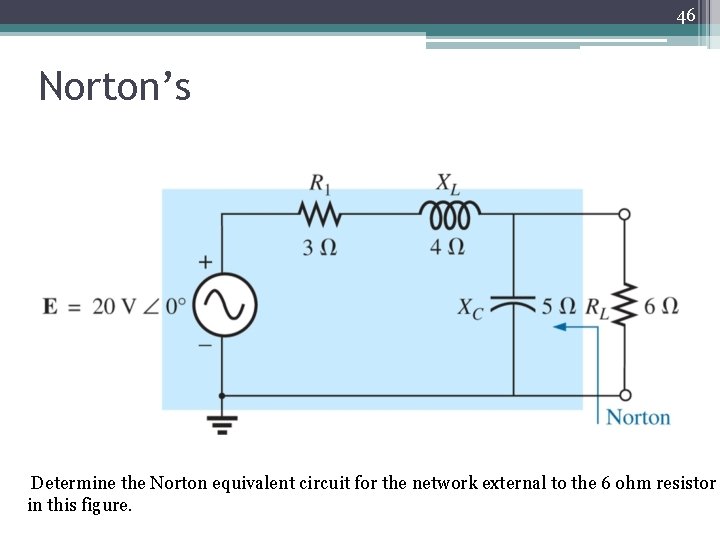
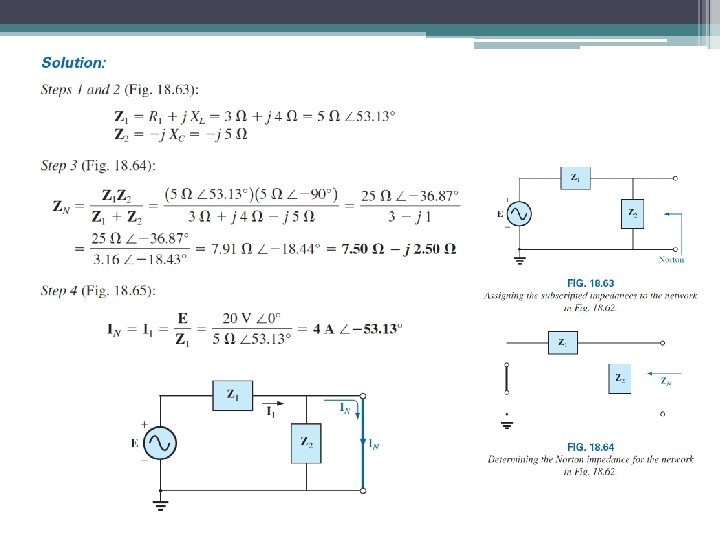
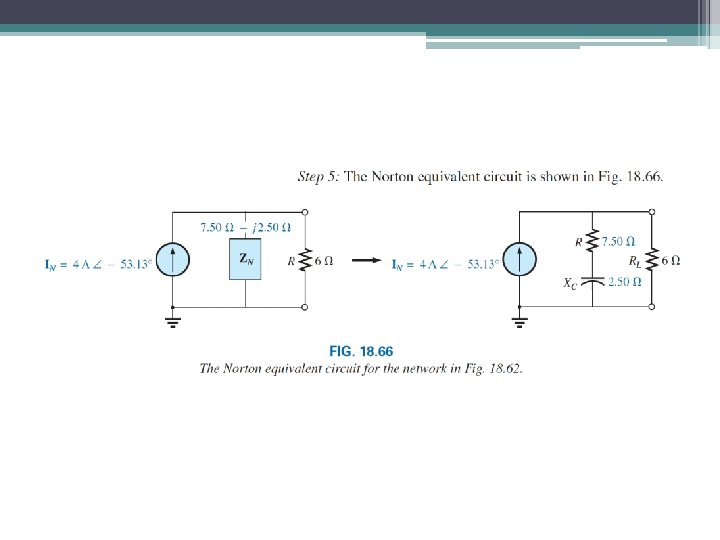
46 Norton’s Determine the Norton equivalent circuit for the network external to the 6 ohm resistor in this figure.

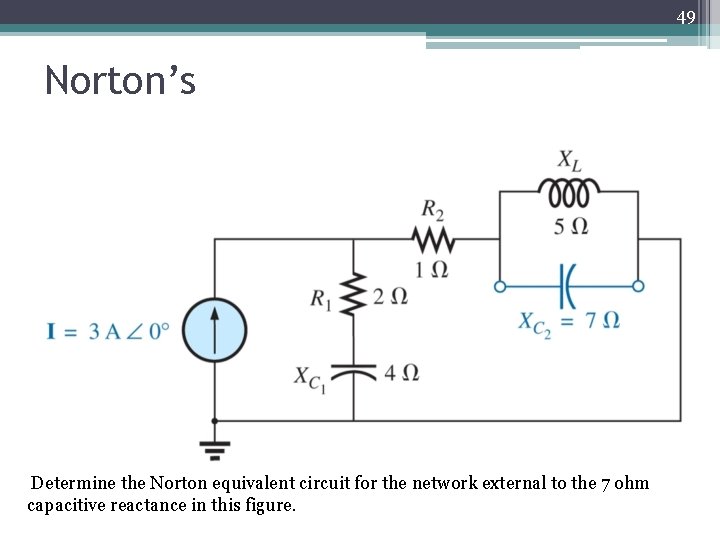
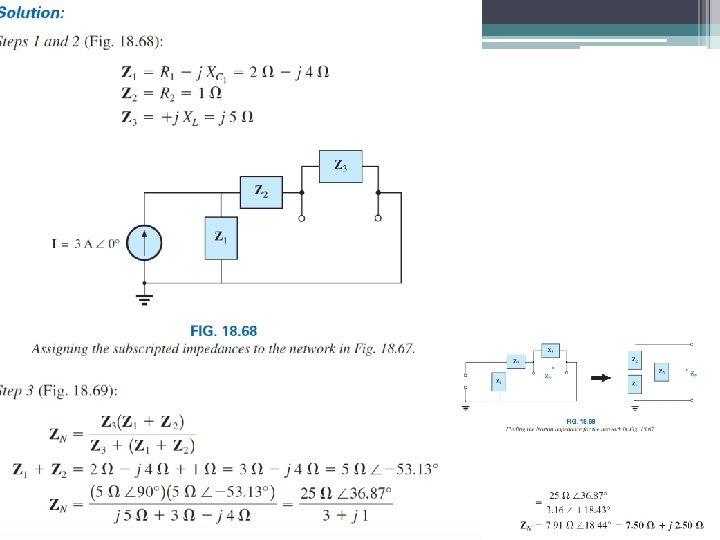
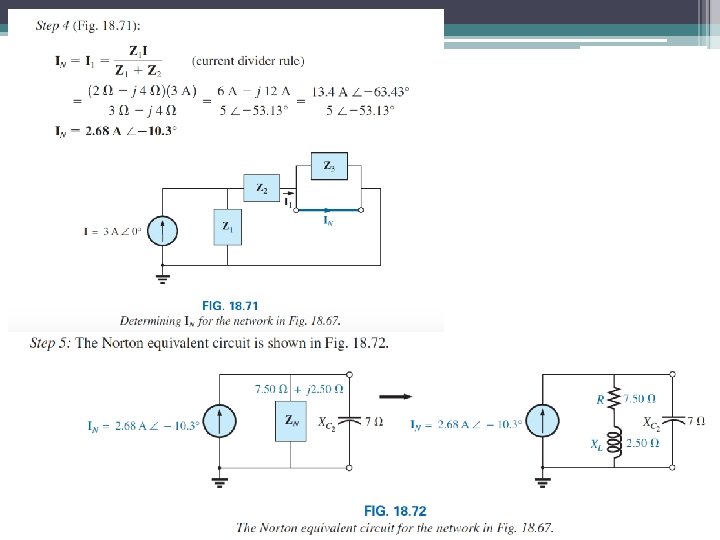
49 Norton’s Determine the Norton equivalent circuit for the network external to the 7 ohm capacitive reactance in this figure.

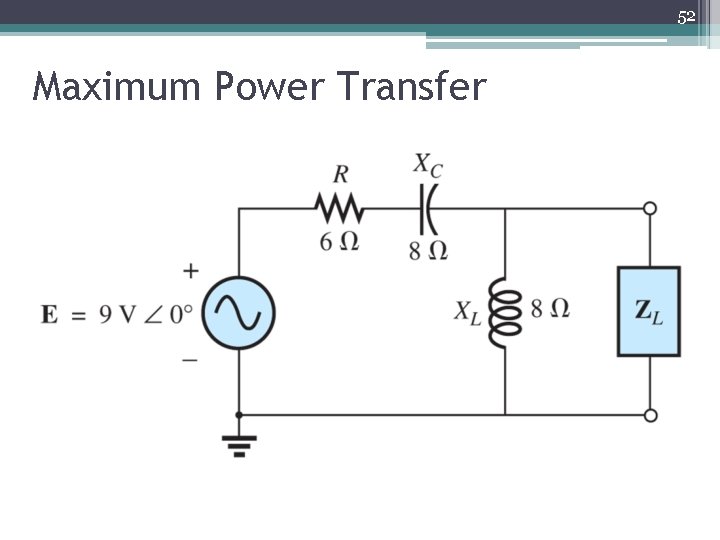
52 Maximum Power Transfer