Viz Glow Training Module Plasma Modeling With Viz

Viz. Glow Training Module Plasma Modeling With Viz. Glow: Low-Temperature Plasma Discharge Theory (Part 1) 1301 S. Capital of Texas Highway Suite B-122 Austin, Texas 78746 www. esgeetech. com September 2015

2 COPYRIGHT AND CONFIDENTIALITY STATEMENT Copyright © (2007 -2015) Esgee Technologies, Inc. All rights reserved. This manual accompanies software that is provided to users under a license agreement. This manual can also be provided under a non-disclosure agreement and is subject to restrictions on confidential information under such an agreement. The manual contains proprietary information and may not be disclosed to a third party not covered by the license agreement or a non-disclosure agreement. No part of this manual may be reproduced in any form or by any means without express written permission from Esgee Technologies, Inc.

3 Collisions and cross sections

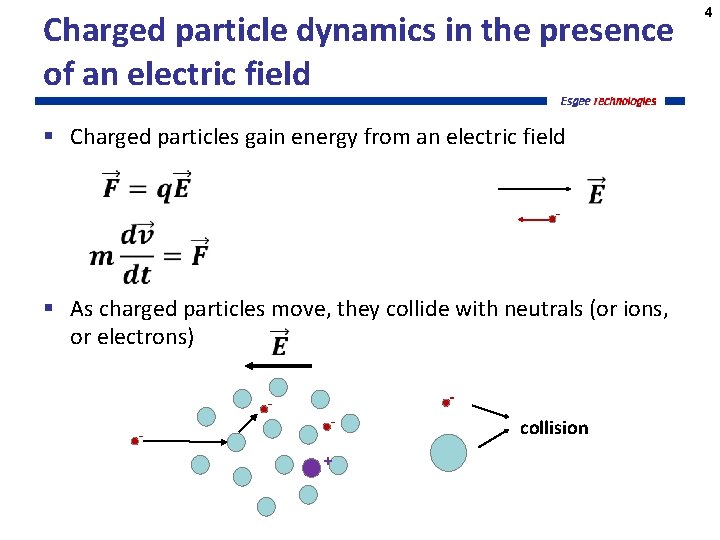
Charged particle dynamics in the presence of an electric field § Charged particles gain energy from an electric field - § As charged particles move, they collide with neutrals (or ions, or electrons) - + collision 4

5 Cross sections § When two particles collide, momentum and (total) energy is conserved § Elastic collision : the kinetic energy of the colliding particles is conserved § Inelastic collision : the kinetic energy of the colliding particles is not conserved (change in internal energy of one or both particles) § The same two colliding particles can produce different results depending on their energies (more specifically, the relative velocity) just before the collision § Cross sections are quantities to help analyze and understand collisions between two or more particles (only considering two body collisions in this section)

6 Collision cross section definition § Number Velocity of test density of test particles relative to particles field particles Electrons “Test particles” (1) Neutrals “Field particles” (2)

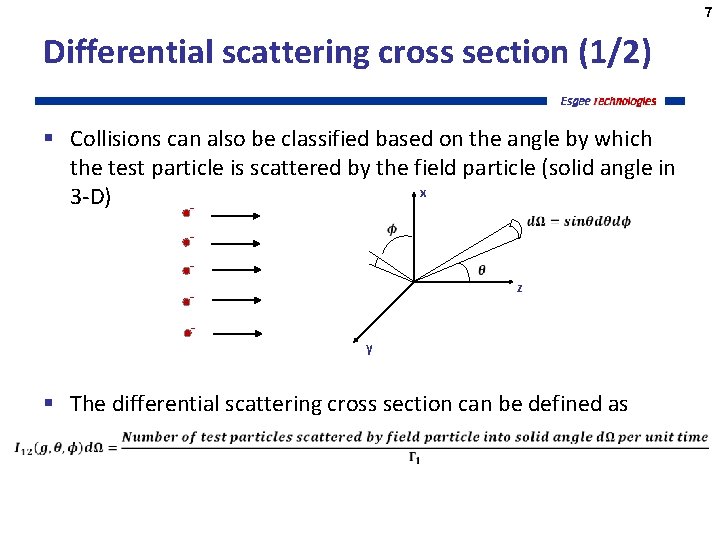
7 Differential scattering cross section (1/2) § Collisions can also be classified based on the angle by which the test particle is scattered by the field particle (solid angle in x 3 -D) z y § The differential scattering cross section can be defined as

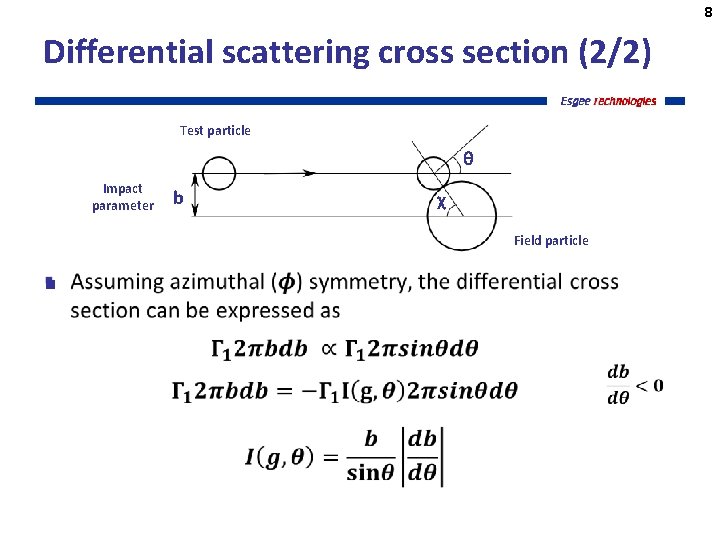
8 Differential scattering cross section (2/2) Test particle θ Impact parameter b χ Field particle §

9 From Differential to Integral cross section §

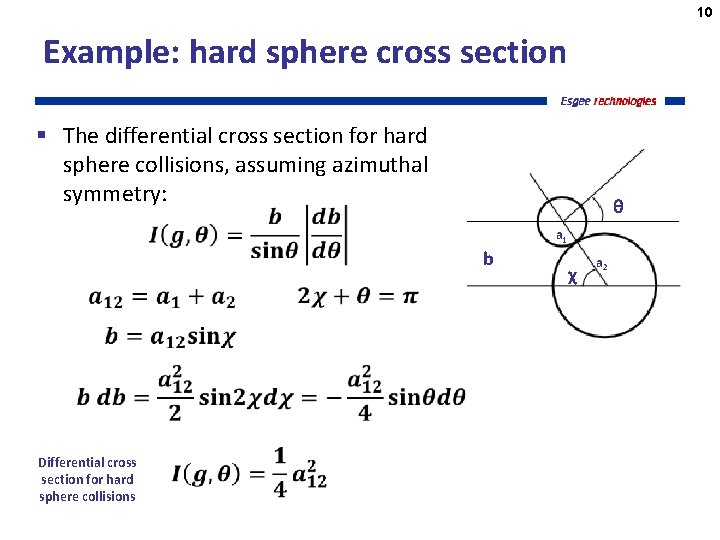
10 Example: hard sphere cross section § The differential cross section for hard sphere collisions, assuming azimuthal symmetry: θ a 1 b Differential cross section for hard sphere collisions χ a 2

Binary collisions: center of mass frame (1/2) § For binary collisions between particles with mass and Collision § The collision can be considered in the center of mass frame Center of mass velocity Relative velocity § From momentum conservation , the center of mass velocity after the collision does not change 11

Binary collisions: center of mass frame (2/2) § For elastic collisions, total kinetic energy is conserved § Transforming to the center of mass frame and simplifying, § For elastic collisions, the magnitude of the relative velocity does not change 12

13 Momentum transfer cross section § The momentum transfer cross section can be defined as § Loss in z-component of momentum flux § Momentum transfer cross section θ § For hard sphere collisions χ

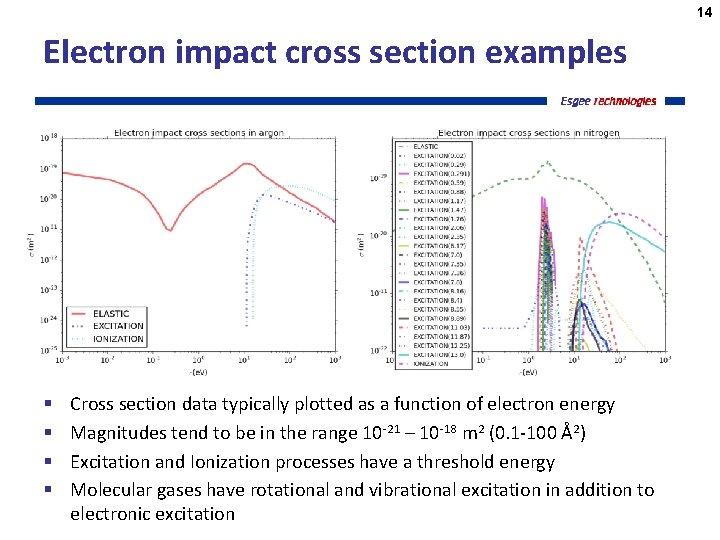
14 Electron impact cross section examples § § Cross section data typically plotted as a function of electron energy Magnitudes tend to be in the range 10 -21 – 10 -18 m 2 (0. 1 -100 Å2) Excitation and Ionization processes have a threshold energy Molecular gases have rotational and vibrational excitation in addition to electronic excitation

15 Collision rate definition §

16 Collision frequency and mean free path §

17 Distribution functions and Boltzmann’s equation

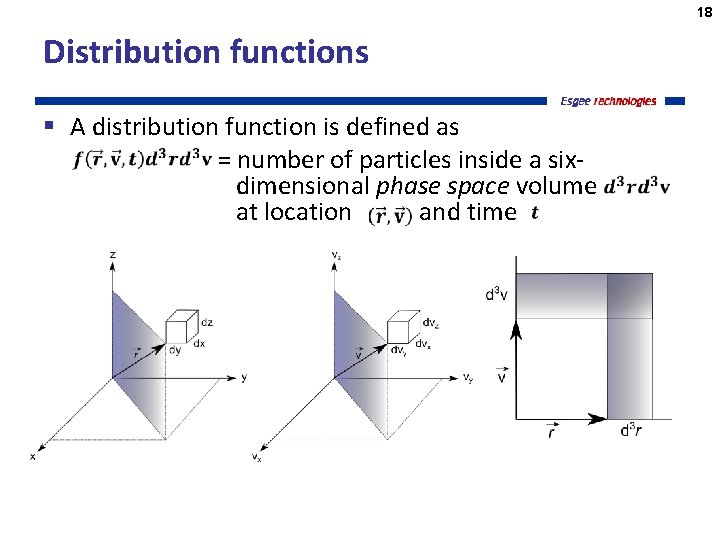
18 Distribution functions § A distribution function is defined as = number of particles inside a sixdimensional phase space volume at location and time

19 The Boltzmann equation § The Boltzmann equation is a continuity equation in phase space with the species distribution function as the dependent variable § For plasmas, the force is given by § The source term of the Boltzmann equation is the “collision integral”

Equilibrium solution: The Maxwellian distribution function § Molecules in a gas reach equilibrium by colliding with other molecules (of the same species) § At equilibrium, the net effect of collisions is zero, i. e Steady No gradients No acceleration § The solution to the Boltzmann equation at equilibrium is the Maxwellian distribution function (velocity distribution function) 20

21 The Maxwellian distribution function § The solution to the Boltzmann equation at equilibrium is the Maxwellian distribution function (velocity distribution function) Isotropic- No dependence on any particular velocity direction § The corresponding speed distribution function is “Tail”

The Electron Energy Distribution Function (EEDF) and Probability Function (EEPF) § Electron Energy Distribution Function Electron Energy Probability Function 22

23 Maxwellian EEPF § “Tail”

Question: why/when is the electron distribution in a plasma not Maxwellian? § Assume electrons in a plasma are initially in equilibrium (characterized by Maxwellian distribution) § If a spatially varying electric field is present (for example in a CCP or DC discharge), individual electrons gain different amounts of energy from the electric field depending on their location, thus representing a perturbation from equilibrium § The mechanism for electrons to reach equilibrium is collisions with other electrons § In a low temperature plasma at intermediate/high pressure, lots more neutrals compared to electrons (weakly ionized), which makes it difficult for electrons to regain equilibrium § High energy electrons colliding with neutrals result in excitation and ionization- loss of energetic electrons (depletion of the “tail”), further distortion from equilibrium § Electron distribution function in low temperature plasmas is non-Maxwellian in many cases § (exceptions- high plasma density discharges, some wave-heated plasmas) 24

25 Solving for the distribution function §

26 The two-term approximation § Isotropic part Anisotropic part Separation of variables - space and time-dependence and velocity(energy) dependence

27 Analytical Solution of the two-term approximation: Maxwellian and Druyvesteyn distributions (1/2) § Collision frequency

28 Analytical Solution of the two-term approximation: Maxwellian and Druyvesteyn distributions (2/2) § The solution can be further simplified by specifying a functional dependence of the collision frequency on the velocity § If the collision frequency is constant (independent of velocity), the isotropic solution is a Maxwellian distribution § If the collision cross section is constant (constant mean free path) , i. e. collision frequency is proportional to velocity, then the isotropic solution is a Druyvesteyn distribution

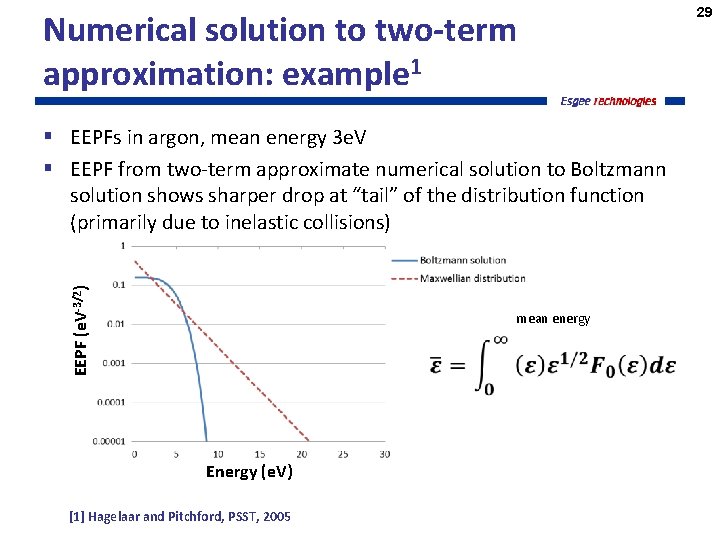
Numerical solution to two-term approximation: example 1 EEPF (e. V-3/2) § EEPFs in argon, mean energy 3 e. V § EEPF from two-term approximate numerical solution to Boltzmann solution shows sharper drop at “tail” of the distribution function (primarily due to inelastic collisions) mean energy Energy (e. V) [1] Hagelaar and Pitchford, PSST, 2005 29

From distribution functions to Macroscopic quantities § Macroscopic quantities can be obtained by taking moments of the distribution function (integrals over velocity space § Number density § Mean velocity § Mean energy density 30

31 Some macroscopic quantities for Maxwellian distribution function § Some macroscopic quantities for Maxwellian distribution function (integrals over velocity space) § Number density § Mean (average) speed § Mean (average) energy density By definition

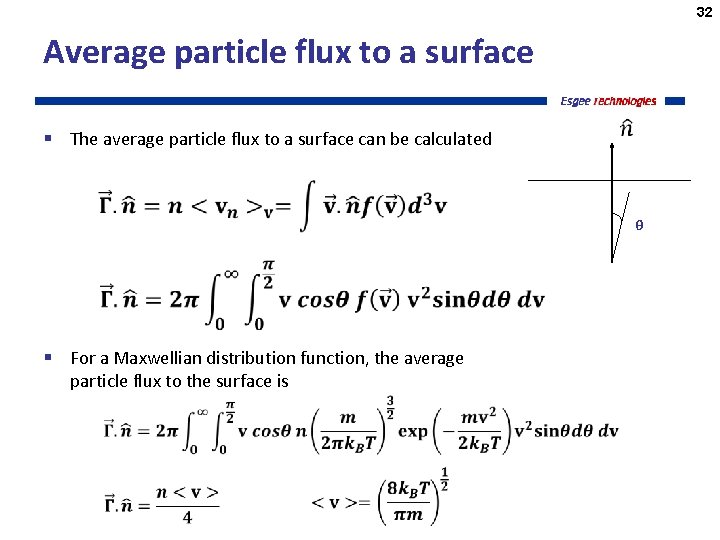
32 Average particle flux to a surface § The average particle flux to a surface can be calculated θ § For a Maxwellian distribution function, the average particle flux to the surface is

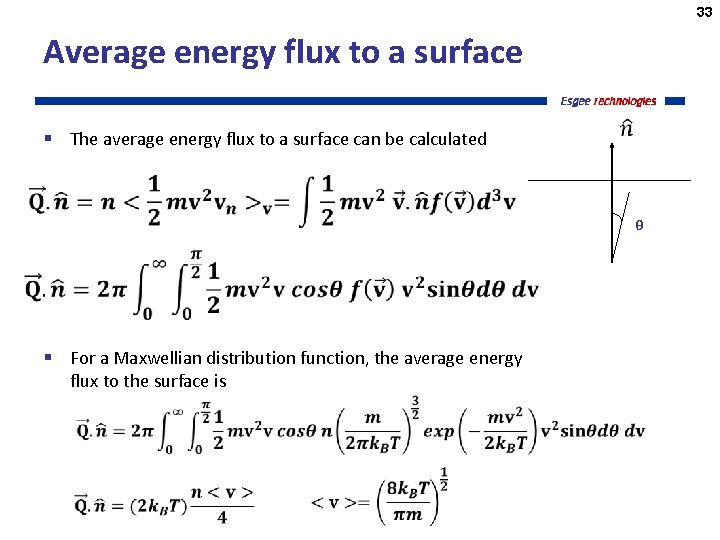
33 Average energy flux to a surface § The average energy flux to a surface can be calculated θ § For a Maxwellian distribution function, the average energy flux to the surface is

34 Fluid models and approximations

The Boltzmann equation and fluid equations § A fluid model of plasmas can be obtained by taking moments of the Boltzmann equation Conservation of mass Conservation of momentum Conservation of energy § The resulting equations are the conservation of mass, momentum and energy of each species ((1+D+1)Nspecies equations, eg 5 Nspecies equations for 3 -D case) 35

36 Conservation of mass (1/3) §

37 Conservation of mass (2/3) Reaction source terms § Integral gives the reaction rate coefficient at a particular temperature

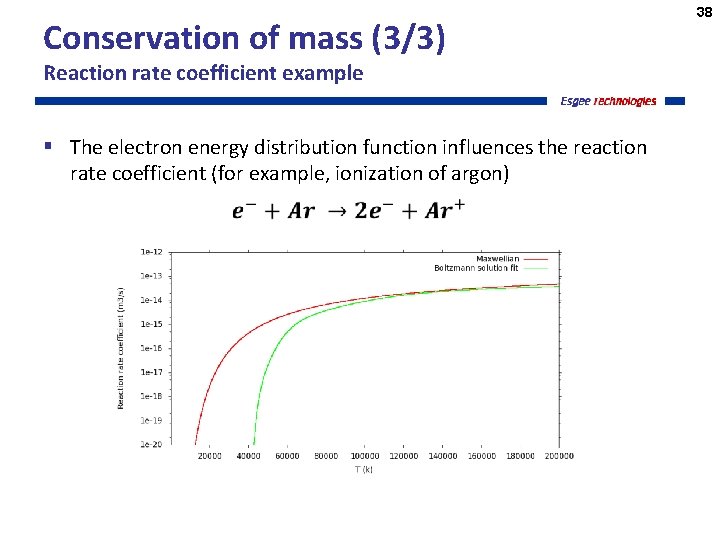
Conservation of mass (3/3) Reaction rate coefficient example § The electron energy distribution function influences the reaction rate coefficient (for example, ionization of argon) 38

39 Conservation of momentum § Inertial terms Electrostatic Force term Pressure Friction/drag term

40 The Drift-Diffusion approximation (1/3) § Starting from the conservation of momentum § If the inertial terms (left hand side) are small compared to the forcing terms Drift-Diffusion approximation Drift term Diffusion term

The Drift-Diffusion approximation (2/3) Einstein’s relation § Drift-Diffusion approximation Mobility Diffusion Coefficient 41

Drift-Diffusion approximation (3/3) From the two-term approximation § The Drift-Diffusion approximation can be derived directly from the two-term approximation of the Boltzmann equation (for electrons)1 § When the distribution function deviates from Maxwellian, then Einstein’s relation is not strictly valid for all cases (but useful approximation where we lack information) [1] Hagelaar and Pitchford, PSST, 2005 42

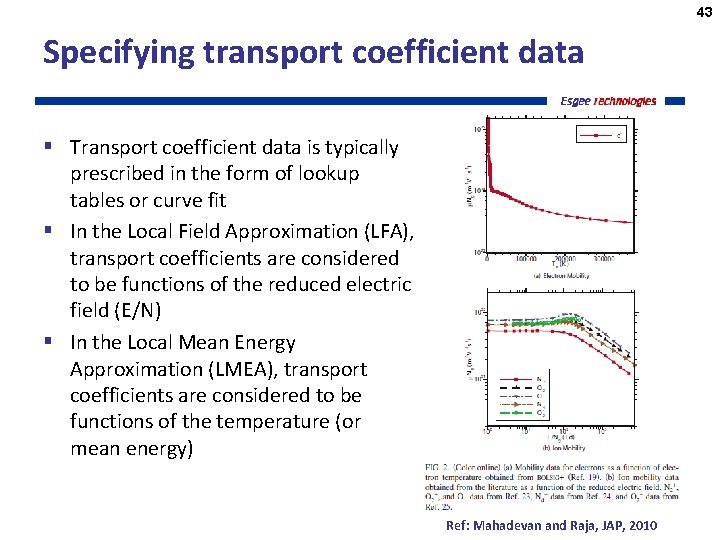
43 Specifying transport coefficient data § Transport coefficient data is typically prescribed in the form of lookup tables or curve fit § In the Local Field Approximation (LFA), transport coefficients are considered to be functions of the reduced electric field (E/N) § In the Local Mean Energy Approximation (LMEA), transport coefficients are considered to be functions of the temperature (or mean energy) Ref: Mahadevan and Raja, JAP, 2010

44 Drift-Diffusion approximation Modification due to magnetic field § For cases where magnetic field effects are important, the conservation of momentum (with inertial terms neglected) is 3 equations, 3 unknowns Drift-Diffusion approximation with magnetic field effect Transport coefficients are tensors

45 Quasi-neutral approximation § The plasma model for species fluxes can be further simplified for cases where quasi-neutrality is assumed Quasi-neutral § To maintain quasi-neutrality, an additional constraint that applies is Assumes no driving current at boundary (floating) Equation for the electric field in terms of density , not strictly consistent with Gauss’ law

46 The ambipolar electric field §

47 The ambipolar diffusion coefficient (1/2) § The species flux expression for the quasi-neutral approximation takes the form (Fick’s law of diffusion) § The resulting effective diffusion coefficient for electrons and ions is called the ambipolar diffusion coefficient § The species conservation equation for the quasi-neutral approximation is

48 The ambipolar diffusion coefficient (2/2) § The ambipolar diffusion coefficient can be simplified further by noting that the electron mobility is much larger than the ion mobility § Using Einstein’s relation § The ambipolar diffusion coefficient can be expressed as

49 Boltzmann relation for electrons § Consider the momentum equation for electrons with inertial terms neglected § If the friction term is also negligible, then the momentum balance is reduced to a force balance between electric field and pressure forces Assume isothermal electrons Boltzmann relation

50 Debye Length Boltzmann electrons and fixed ions § Sheet of negative charge x x Debye length

51 Conservation of energy § convection terms Thermal flux Joule heating Energy source term due to collisions

End of presentation www. esgeetech. com