UNIDAD 5 CAPTULO VII FORMAS CANNICAS Y MATRIZ

















































- Slides: 49

UNIDAD 5. CAPÍTULO VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Considere los resultados del siguiente sistema: en el que los vectores característicos y las soluciones (también llamadas modos característicos) correspondientes son:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Para obtener otros vectores característicos solamente se multiplica cualquiera de ellos por una constante. Este procedimiento sólo cambia el tamaño del vector. Por ejemplo, si se quiere que el 1 er componente de cada vector sea la unidad, se divide el vector característico original entre dos: Si se requieren vectores característicos unitarios, cada uno de ellos se divide entre su longitud (la raíz cuadrada de la suma de los cuadrados de sus componentes).

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. es decir: A continuación se probará que los vectores característicos unitarios resultan bastante útiles en la resolución de sistemas de ecuaciones.

DIAGONALIZACIÓN.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Las variables de estado x e y se pueden considerar como dos coordenadas en un sistema de dos ejes coordenados. Este sistema se denomina espacio de estado, concepto que puede generalizarse a cualquier número de variables de estado; aunque, cuando hay más de tres, pierde su significado geométrico. Considere los siguientes vectores característicos K 1 y K 2 normalizados de manera que su primer componente sea 1:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. El comportamiento del sistema se debe a la combinación vectorial del movimiento de cada modo característico a lo largo de su vector característico, Estos movimientos que ocurren con diferente rapidez la cual está determinada por la constante de tiempo del modo característico. La proyección de la condición inicial x(0) sobre cada vector característico determina la magnitud inicial asociada con el modo característico. Si x(0) está colocado exactamente sobre uno de los vectores característicos, sólo ese modo característico aparecerá en el movimiento.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Los vectores característicos (linealmente independientes) pueden usarse para formar un nuevo conjunto de ejes coordenados. Sean z 1 y z 2 las nuevas coordenadas y e 1, e 2 los vectores base unitarios, que se obtienen al normalizar los vectores K 1 y K 2 y dividirlos entre sus longitudes. Es decir: El vector solución x , expresado en estas coordenadas es:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. y su derivada: La respuesta debe satisfacer x´ = Ax; por tanto, donde z 1 y z 2 son escalares. Por la definición de vectores característicos, e 1 y e 2 deben satisfacer: entonces, y comparando componentes se tiene:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Lo que muestra que el sistema homogéneo de ecuaciones diferenciales se desacopla al expresarse en términos de los ejes coordenados a lo largo de las direcciones de los vectores característicos. Usando álgebra lineal se puede probar que la matriz de transformación entre los sistemas de coordenadas x y z es la matriz modal M, cuyas columnas son los vectores característicos. en este caso se tiene: donde x = M z, lo que implica que x´ = M z´.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. A partir del sistema no homogéneo se obtiene: Es posible mostrar que M 1 existe para el caso de valores característicos distintos, entonces, en donde: propiedad que también es válida para el caso de vectores generales, si los valores característicos de A son distintos; es decir,

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. donde L es una matriz diagonal cuyos elementos son los valores característicos del sistema; entonces, el conjunto de ecuaciones en términos del vector z es: Para el caso de orden n, la matriz modal tiene la forma: La matriz L se llama matriz desacoplante porque las ecuaciones diferenciales que resultan en términos de las variables en el vector z están desacopladas o son independientes si los valores característicos son distintos.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Ejemplo: Obtenga la solución del sistema: desacoplando las ecuaciones. Solución: Los valores y vectores característicos de este sistema obtenidos anteriormente son l 1 = 1, l 2 = 2 y entonces, la matriz modal y su inversa son:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. La matriz desacoplante es: Usando la transformación x = M z se obtiene: se obtiene el siguiente sistema desacoplado: dos ecuaciones independientes de 1 er orden que pueden resolverse usando métodos apropiados.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Las soluciones son: La solución en las variables originales se obtiene usando la transformación x = M z: o

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Valores característicos repetidos. Puede ser que este caso no tenga vectores característicos linealmente independientes, por lo que la matriz L no será diagonal. Para un sistema de segundo orden que tenga el valor característico l 1 repetido una vez, se puede mostrar que la matriz tiene la forma: donde el subíndice R distingue LR de la matriz L usada para el caso de valores característicos distintos.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. La extensión de este concepto al caso de 3 er orden en el que el valor característico l 1 se repita dos veces, se obtiene: Para el caso del 3 er orden en el que el valor característico l 1 se repite una vez, y el otro es l 2, se tiene:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Ejemplo: Obtenga la solución del sistema: desacoplando las ecuaciones. Solución: Los valores y vectores característicos de este sistema son l 1 = l 2 = 3 y entonces, la matriz modal y su inversa son:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. La matriz desacoplante es: Usando la transformación x = M z se obtiene: el siguiente sistema desacoplado: La 2ª es una ecuación independiente de 1 er orden que se resuelve usando el método de variables separables.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. La solución es: La 1ª ecuación depende de la 2ª, pero también es de 1 er orden y su solución es: La solución en las variables originales se obtiene usando la transformación x = M z: o

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Valores característicos complejos. Este caso se inscribe en el de valores característicos distintos; sin embargo, los vectores característicos y los elementos diagonales de la matriz L serán complejos. La interpretación física de los modos característicos es difícil dado que los vectores característicos ya no son ejes coordenados en el plano real de variables de estado; así mismo, para algunos propósitos de cálculo, es deseable evitar cantidades complejas. Por tanto, este problema se puede explicar desde un punto de vista ligeramente diferente.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Considere el caso de 2° orden en el que la matriz A tiene los valores característicos l = a ib, b > 0, en el que se puede mostrar que los vectores característicos K 1 y K 2 son complejos conjugados, de modo que: En lugar de la matriz modal M, definida anteriormente, se usa la matriz: MC tiene elementos reales y tiene la propiedad: o

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Entonces, y reacomodando en forma matricial : donde: Ahora, usando la transformación x = MCz, la ecuación de estado x´ = A x + B f se convierte (para 2° orden) en:

FORMA CANÓNICA DE JORDAN.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Para valores característicos distintos el modelo de estado se transforma en una matriz diagonal, lo que no siempre es posible cuando los valores se repiten. Éstas son las formas canónicas de la ecuación de estado. Para sistemas de orden superior, se puede encontrar una matriz de transformación M para obtener la siguiente forma canónica de Jordan: donde ai, i = 1, , n 1, puede ser cero o uno.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Por ejemplo, un sistema de 3 er orden con dos raíces repetidas l 1 y una raíz distinta l 2 da la forma: donde: LD = l 2 y En general, L es un bloque de submatrices de la matriz canónica Li para cada conjunto de modos del sistema.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Dos raíces repetidas corresponden a un conjunto de dos modos usualmente acoplados y LR es una matriz 2 2. Para tres raíces repetidas, Li es de 3 3, y así sucesivamente. Para cada raíz distinta, Li = li. Con raíces complejas, la forma de Jordan tiene elementos complejos y a veces se escribe usando la forma LC. Por ejemplo, un modelo 6° orden con dos raíces repetidas l 1, dos complejas, a ib y dos distintas l 5 y l 6. Si los vectores característicos correspondientes a l 1 son dependientes, la forma modificada de Jordan es:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. La forma canónica se aplica en ingeniería, por ejemplo, para el diseño de un controlador para suministro de fuerza, un par de torsión, un voltaje o una presión para mover un sistema de tal manera que la señal de salida sea función del tiempo.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. En la articulación del hombro de un brazo de robot accionado por un motor eléctrico; la señal de entrada es el voltaje del motor y la de salida es el ángulo del hombro. Para predecir si la señal de salida puede asumir algún valor deseado, se requiere entender la controlabilidad del sistema. Un estado x 1 = x(t 1) de un sistema es controlable si el vector de entrada puede transferir un estado x 0 = x(t 0) en cualquier momento antes de x 1 en un tiempo finito. Si todos los estados x 1 del sistema son controlables, el sistema también lo es. La matriz canónica es muy útil para evaluar la controlabilidad.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. El modelo de primer orden: es controlable si b ≠ 0. Para demostrarlo, use la solución general: La controlabilidad exige que se pueda obtenerse un valor deseado de x(t) en cualquier momento t, para valores arbitrarios de x(t 0) y t 0. Una entrada constante f puede realizar esta tarea si no restringe su magnitud. Para verlo, haga la integración para f arbitraria pero constante, y despeje f.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Al considerar sistemas de orden superior, las propiedades de controlabilidad no siempre son evidentes. Considere el sistema de segundo orden: Se puede ver que el estado x 1 es controlable porque su ecuación no depende de x 2; pero la situación para x 2 no es clara. La respuesta se encuentra recordando que los modos de un modelo forman la estructura de su comportamiento dinámico.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Para controlar el comportamiento del sistema, se debe influir por separado en cada uno de sus modos; por tanto, examínese la composición modal del modelo. Los valores característicos son l = 1, 2, y los vectores característicos son: La matriz de transformación modal M y su inversa son:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Los modos son: z = M 1 x, o Las ecuaciones modales son: o Dado que ni f(t) ni z 2 aparecen en la 1ª ecuación modal, el modo z 1 es incontrolable; por tanto, el sistema es incontrolable.

MATRIZ DE TRANSICIÓN.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Recuérdese que las columnas de la matriz fundamental Y(t) son los vectores solución linealmente independientes x 1, x 2, . . . , xn de un sistema. La respuesta libre se puede expresar en la forma: Se define así una nueva matriz, llamada matriz de transicion, como: Entonces, y, para calcular F(t) se desarrolla un método alterno.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Solución a partir de los modos característicos. Considere la forma diagonal del vector z para valores característicos distintos. Con f(t) = 0, la ecuación para cada coordenada modal zi es: Es posible mostrar que la respuesta libre es: o, en forma matricial:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. y si la matriz de exponenciales anterior se representa por FM(t), entonces: La matriz FM(t) es la matriz de transicion modal, la cual describe la transición en el tiempo de cada coordenada modal de un punto otro. La forma diagonal se obtuvo por la transformación: Entonces: y

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Con lo que se recupera la respuesta libre de la ecuación: en términos de las variables de estado originales. En analogía con el caso de 1 er orden se escribe: donde la matriz de transición de estado está dada por: que describe otra forma de obtener la matriz de transición de estado, análoga a la función eat para la ecuación de 1 er orden x´ = ax. Si A es de n n, también lo es F(t).

PROPIEDADES DE LA MATRIZ DE TRANSICIÓN DE ESTADO.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Es posible deducir algunas propiedades de la matriz de transición estado a partir de las ecuaciones: Haciendo t = 0 en la 1ª ecuación se muestra que: Así, o Entonces, al despejar FM(t) de la 2ª ecuación:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. La inversa de M se obtiene invirtiendo los elementos de la diagonal. Como FM(t) es diagonal y los valores característicos son distintos, (FM) 1 = FM( t). De aquí resulta que: Propiedad que evita la necesidad de realizar los cálculos para encontrar la inversa de la matriz. La solución, en términos del estado en cualquier tiempo, por ejemplo t 1 también se puede escribir como: pero

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. entonces: o bien: Al comparar las dos últimas ecuaciones se prueba que: para cualquier t y t 1; asimismo, como F(t + t 1) = F(t 1 + t), se mantiene la propiedad conmutativa. Entonces, Finalmente, haciendo t = t 1 = D, se observa que:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. o, en general, Propiedad útil para soluciones numéricas, ya que las computadoras pueden multiplicar matrices rápidamente. Ejemplo. Matriz de transición para un sistema resortemasa-amortiguador. i) Obtenga la matriz de transición para un sistema resortemasa-amortiguador (m = 1, g = 7 y = 10) cuyo modelo es: ii) Determine el desplazamiento x 1 = x y la velocidad x 2 = x´ de la masa en t = 0. 1 y t = 0. 2, si se establecen x 1(0) = 3 y x 2(0) = 0, como condiciones iniciales.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. iii) Si en t = 0. 1, x 1(0. 1) = 0. 50 y x 2(0. 1) = 0. 21, ¿qué condiciones iniciales produjeron este movimiento? Solución: i) El polinomio característico es l 2 + 7 l + 10 = 0, los valores característicos son l 1, 2 = 2 y 5 y los vectores característicos pueden normalizarse como: la matriz de transformación modal con su inversa son:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. La matriz de transición modal es: y la matriz de transición de estado: ii) Para t = 0. 1 Para t = 0. 2

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. iii) Dada x(0. 1) y usando la propiedad F 1(t) = F( t) se puede obtener x(0) lo que resulta en

SOLUCIÓN POR SERIES PARA LA MATRIZ DE TRANSICIÓN.

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. La forma escalar de la ecuación vectorial: es: y su solución es: Pero la función eat se puede representar como la serie: Por tanto, tiene sentido probar la siguiente solución en series para F(t), que es la solución de:

U-5. CAP. VII. FORMAS CANÓNICAS Y MATRIZ DE TRANSICIÓN. Lo que se puede probar derivando la serie término a término. La analogía con la expansión en serie para la exponencial escalar eat permite llamar a la matriz de transición F(t) como matriz exponencial y se simboliza como e. At. Esta representación permite especialmente calcular la matriz de transición para un valor particular de t con una computadora, debido a que sólo necesita la multiplicación repetida de la matriz A.
 Cannicas
Cannicas Cannicas
Cannicas Https://slidetodoc.com/captulo-2-o-sudeste-e-o-sul-do/
Https://slidetodoc.com/captulo-2-o-sudeste-e-o-sul-do/ Conceito de judaismo
Conceito de judaismo Unidades decenas y centenas
Unidades decenas y centenas Formas compuestas indicativo
Formas compuestas indicativo Verbos en gerundio y participio
Verbos en gerundio y participio Vii s
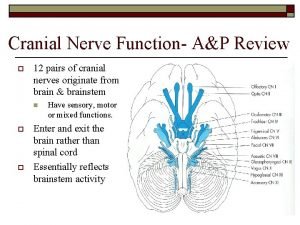
Vii s Vestibulocochlear nerve.
Vestibulocochlear nerve. Group 7 elements
Group 7 elements Inferno canto vii
Inferno canto vii 6/1996. (vii. 16.) müm rendelet
6/1996. (vii. 16.) müm rendelet Animale care fac oua
Animale care fac oua Canto viii paradiso
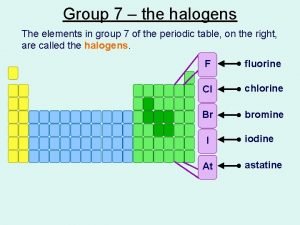
Canto viii paradiso F,cl,br,i
F,cl,br,i Rima xxix
Rima xxix Reach annex vii
Reach annex vii Hikayat hang tuah bab 2
Hikayat hang tuah bab 2 Vii=i solucion
Vii=i solucion Lettera vii platone
Lettera vii platone Vii informe foessa
Vii informe foessa Reforma gregoriańska
Reforma gregoriańska Title vii of the civil rights act
Title vii of the civil rights act Clasa bazidiomicete
Clasa bazidiomicete Soarele de dupa vii isi arata fata
Soarele de dupa vii isi arata fata Code of ethics for professional teachers article 2
Code of ethics for professional teachers article 2 Dr margaret henry
Dr margaret henry Fragment 2 for composition vii, 1913.
Fragment 2 for composition vii, 1913. 17
17 Origen aparente del 5 par craneal
Origen aparente del 5 par craneal Descompunatori
Descompunatori Tema poeziei de ce nu-mi vii
Tema poeziei de ce nu-mi vii Rima vii becquer comentario
Rima vii becquer comentario Nerf 7 bis
Nerf 7 bis So4 lr6
So4 lr6 Odpalanie palnika acetylenowo-tlenowego
Odpalanie palnika acetylenowo-tlenowego Nerfs vii
Nerfs vii Sherwood engineering receiver
Sherwood engineering receiver Handouts definition
Handouts definition Cranial nerve 7 sensory test
Cranial nerve 7 sensory test 10/2015 (vii. 30) hm
10/2015 (vii. 30) hm Triboron octachloride formula
Triboron octachloride formula King henry vii family tree
King henry vii family tree Representative of halogen group
Representative of halogen group Title vii of the civil rights act
Title vii of the civil rights act Eng qadimgi adabiy yodgorliklar
Eng qadimgi adabiy yodgorliklar Pearson vii
Pearson vii What is the theme of the poem song vii
What is the theme of the poem song vii Henryk vii tudor
Henryk vii tudor Hamlet; act iv; scene v; place
Hamlet; act iv; scene v; place