Topological Strings and Knot Homologies Sergei Gukov Outline




![Holomorphic Anomaly [M. Bershadsky, S. Cecotti, H. Ooguri, C. Vafa] (determines up to holomorphic Holomorphic Anomaly [M. Bershadsky, S. Cecotti, H. Ooguri, C. Vafa] (determines up to holomorphic](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-6.jpg)



![Open String Field Theory N D-branes [E. Witten] A-model: U(N) Chern-Simons gauge theory B-model: Open String Field Theory N D-branes [E. Witten] A-model: U(N) Chern-Simons gauge theory B-model:](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-11.jpg)


![Large N Duality [R. Gopakumar, C. Vafa] Large N Duality [R. Gopakumar, C. Vafa]](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-14.jpg)
![Large N Duality [R. Gopakumar, C. Vafa] N D-branes U(N) Chern-Simons theory on Closed Large N Duality [R. Gopakumar, C. Vafa] N D-branes U(N) Chern-Simons theory on Closed](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-15.jpg)
![Counting BPS states: 5 d [R. Gopakumar, C. Vafa] M-theory on M 2 -brane Counting BPS states: 5 d [R. Gopakumar, C. Vafa] M-theory on M 2 -brane](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-16.jpg)


![Gromov-Witten Invariants via Gauge Theory X symplectic 4 -manifold [C. Taubes] topological twist of Gromov-Witten Invariants via Gauge Theory X symplectic 4 -manifold [C. Taubes] topological twist of](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-20.jpg)
![Gromov-Witten Invariants via Gauge Theory [D. Maulik, N. Nekrasov, A. Okounkov, R. Pandharipande] X Gromov-Witten Invariants via Gauge Theory [D. Maulik, N. Nekrasov, A. Okounkov, R. Pandharipande] X](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-21.jpg)







![Knot Homologies • Knot Floer homology: Example: [P. Ozsvath, Z. Szabo] [J. Rasmussen] Knot Homologies • Knot Floer homology: Example: [P. Ozsvath, Z. Szabo] [J. Rasmussen]](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-33.jpg)
![Knot Homologies • Khovanov homology: [M. Khovanov] Example: 3 2 1 0 i 1 Knot Homologies • Khovanov homology: [M. Khovanov] Example: 3 2 1 0 i 1](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-34.jpg)
![Knot Homologies • sl(N) knot homology: N=3: “foams” (web cobordisms) [M. Khovanov] N>2: matrix Knot Homologies • sl(N) knot homology: N=3: “foams” (web cobordisms) [M. Khovanov] N>2: matrix](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-35.jpg)





![What’s Next? • Generalization to other groups and representations [S. G. , J. Walcher] What’s Next? • Generalization to other groups and representations [S. G. , J. Walcher]](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-47.jpg)






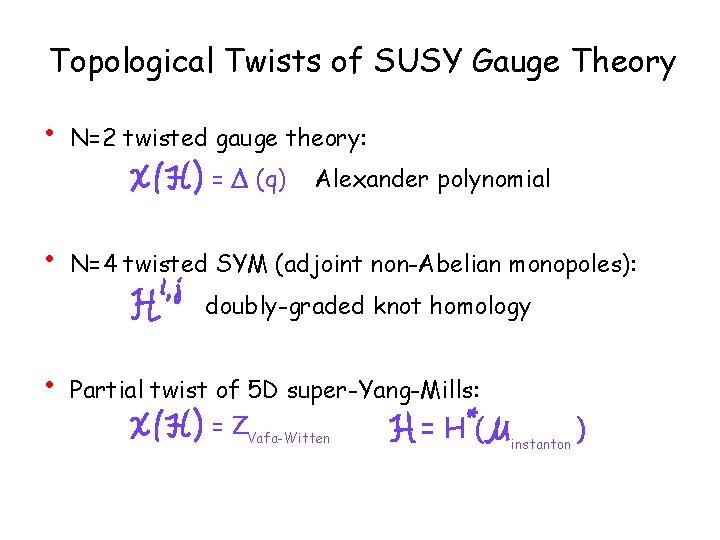


- Slides: 65

Topological Strings and Knot Homologies Sergei Gukov

Outline • Introduction to Topological String Theory • Relation to Knot Homologies based on: S. G. , A. Schwarz, C. Vafa, hep-th/0412243 N. Dunfield, S. G. , J. Rasmussen, math. GT/0505662 S. G. , J. Walcher, hep-th/0512298 joint work with E. Witten

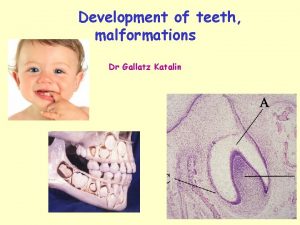
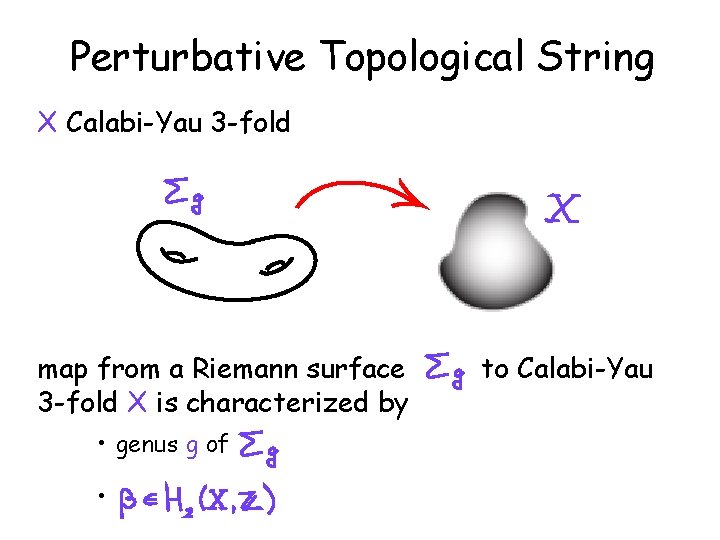
Perturbative Topological String X Calabi-Yau 3 -fold map from a Riemann surface 3 -fold X is characterized by • genus g of • to Calabi-Yau

Perturbative Topological String Topological string partition function: A-model: Kahler moduli “number” of holomorphic maps of genus g curves to X which land in class

Perturbative Topological String B-model: symplectic basis of 3 -cycles holomorphic Ray-Singer torsion
![Holomorphic Anomaly M Bershadsky S Cecotti H Ooguri C Vafa determines up to holomorphic Holomorphic Anomaly [M. Bershadsky, S. Cecotti, H. Ooguri, C. Vafa] (determines up to holomorphic](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-6.jpg)
Holomorphic Anomaly [M. Bershadsky, S. Cecotti, H. Ooguri, C. Vafa] (determines up to holomorphic ambiguity)

Wave Function Interpretation quantization of symplectic structure Wave Function depends on (choice of polarization) [E. Witten]

Mirror Symmetry

Applications • Physical Applications • compute F-terms in string theory on X [H. Ooguri, A. Strominger, C. Vafa], … • Black Hole physics • dynamics of SUSY gauge theory [R. Dijkgraaf, C. Vafa], … • Mathematical Applications • • • Enumerative geometry Homological algebra Low-dimensional topology Representation theory Gauge theory

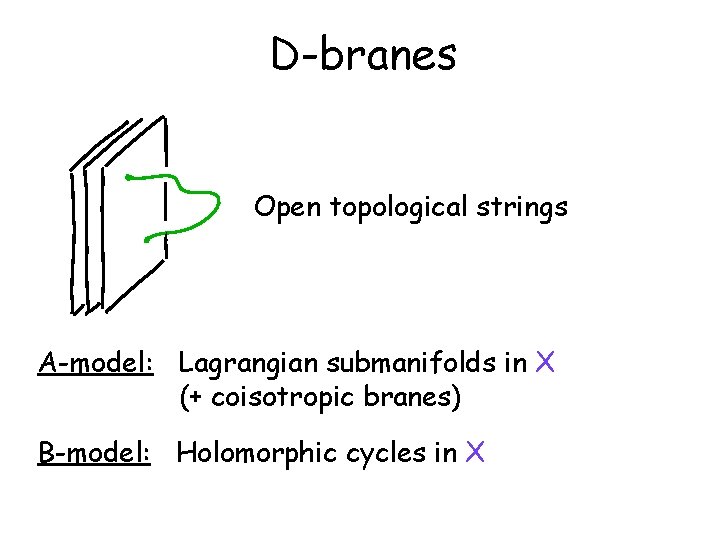
D-branes Open topological strings A-model: Lagrangian submanifolds in X (+ coisotropic branes) B-model: Holomorphic cycles in X
![Open String Field Theory N Dbranes E Witten Amodel UN ChernSimons gauge theory Bmodel Open String Field Theory N D-branes [E. Witten] A-model: U(N) Chern-Simons gauge theory B-model:](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-11.jpg)
Open String Field Theory N D-branes [E. Witten] A-model: U(N) Chern-Simons gauge theory B-model: 6 d: holomorphic Chern-Simons [R. Dijkgraaf, C. Vafa] 2 d: BF theory 0 d: Matrix Model

Homological Mirror Symmetry A-branes: objects in the Fukaya category Fuk (X) B-branes: objects in the derived category of coherent sheaves homological mirror symmetry: Fuk (X) [M. Kontsevich]

Matrix Factorizations B-branes at Landau-Ginzburg point are described by matrix factorizations Topological Landau-Ginzburg model with superpotential W CY-LG correspondence: MF (W)
![Large N Duality R Gopakumar C Vafa Large N Duality [R. Gopakumar, C. Vafa]](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-14.jpg)
Large N Duality [R. Gopakumar, C. Vafa]
![Large N Duality R Gopakumar C Vafa N Dbranes UN ChernSimons theory on Closed Large N Duality [R. Gopakumar, C. Vafa] N D-branes U(N) Chern-Simons theory on Closed](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-15.jpg)
Large N Duality [R. Gopakumar, C. Vafa] N D-branes U(N) Chern-Simons theory on Closed topological string on resolved conifold
![Counting BPS states 5 d R Gopakumar C Vafa Mtheory on M 2 brane Counting BPS states: 5 d [R. Gopakumar, C. Vafa] M-theory on M 2 -brane](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-16.jpg)
Counting BPS states: 5 d [R. Gopakumar, C. Vafa] M-theory on M 2 -brane on number of BPS states with charge Example (conifold): and spin g

Counting BPS states: 4 d Type II string theory on X [H. Ooguri, A. Strominger, C. Vafa] number of BPS states of 4 d black hole with electric charge q and magnetic charge p evaluated at , the attractor value

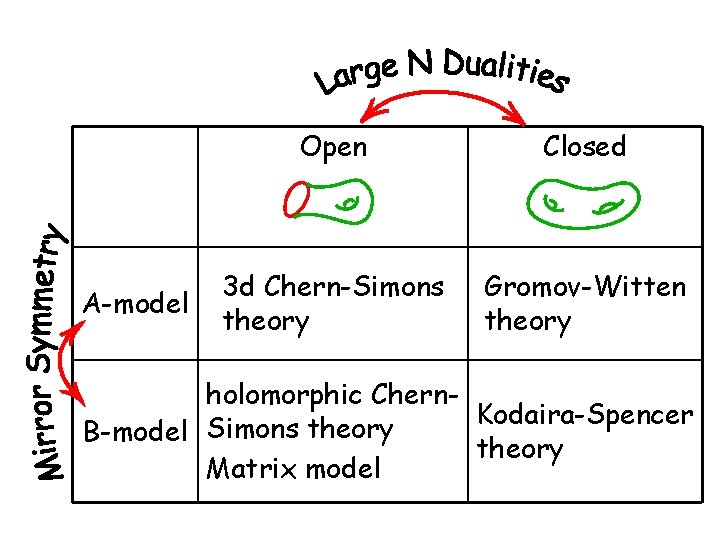
A-model Open Closed 3 d Chern-Simons theory Gromov-Witten theory holomorphic Chern. Kodaira-Spencer Simons theory B-model theory Matrix model

Computing non-compact (toric) holomorphic anomaly relative Gromov-Witten large N duality heterotic/type IIA duality gauge theory compact small g (ambiguity) (in practice only small g) ? partial results for all g ?
![GromovWitten Invariants via Gauge Theory X symplectic 4 manifold C Taubes topological twist of Gromov-Witten Invariants via Gauge Theory X symplectic 4 -manifold [C. Taubes] topological twist of](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-20.jpg)
Gromov-Witten Invariants via Gauge Theory X symplectic 4 -manifold [C. Taubes] topological twist of N=2 abelian gauge theory with a hypermultiplet
![GromovWitten Invariants via Gauge Theory D Maulik N Nekrasov A Okounkov R Pandharipande X Gromov-Witten Invariants via Gauge Theory [D. Maulik, N. Nekrasov, A. Okounkov, R. Pandharipande] X](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-21.jpg)
Gromov-Witten Invariants via Gauge Theory [D. Maulik, N. Nekrasov, A. Okounkov, R. Pandharipande] X Calabi-Yau 3 -fold topological twist of abelian gauge theory in six dimensions: localizes on singular U(1) instantons (ideal sheaves)

Enumerative Invariants Rational (maps) Closed Open Refinement Integer (gauge theory, embeddings) GW DT/GV Equivariant (stable maps) (ideal sheaves) open GW Knot BPS invariants (relative Homologies stable maps)

Polynomial Knot Invariants • In Chern-Simons theory Wilson loop operator polynomial in q • Quantum groups & R-matrix [E. Witten]

Polynomial Knot Invariants • Jones polynomial: unknot Example:

Polynomial Knot Invariants • Quantum sl(N) invariant: unknot

Polynomial Knot Invariants • HOMFLY polynomial: unknot

Polynomial Knot Invariants • HOMFLY polynomial: unknot Example:

Polynomial Knot Invariants • Alexander polynomial: unknot Example:

• Question (M. Atiyah): Why integer coefficients?

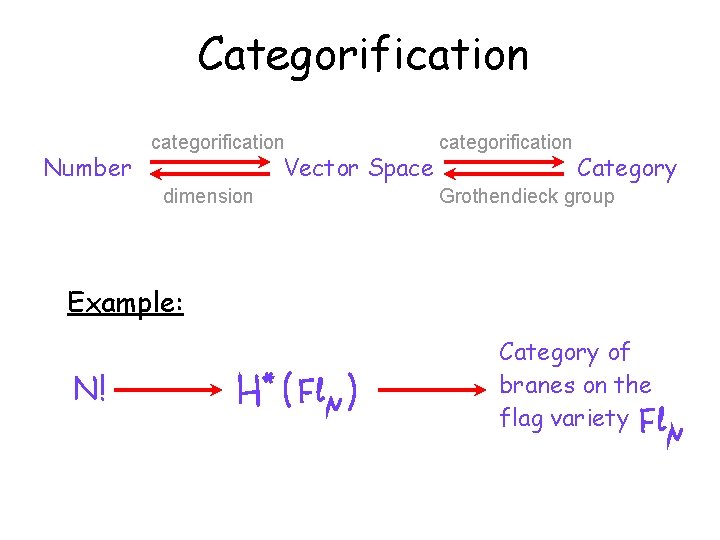
Categorification Number categorification Vector Space dimension categorification Category Grothendieck group

Categorification Number categorification Vector Space dimension categorification Category Grothendieck group Example: N! Category of branes on the flag variety

Categorification Number categorification Vector Space dimension categorification Category Grothendieck group • Knot homology Euler characteristic = polynomial knot invariant
![Knot Homologies Knot Floer homology Example P Ozsvath Z Szabo J Rasmussen Knot Homologies • Knot Floer homology: Example: [P. Ozsvath, Z. Szabo] [J. Rasmussen]](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-33.jpg)
Knot Homologies • Knot Floer homology: Example: [P. Ozsvath, Z. Szabo] [J. Rasmussen]
![Knot Homologies Khovanov homology M Khovanov Example 3 2 1 0 i 1 Knot Homologies • Khovanov homology: [M. Khovanov] Example: 3 2 1 0 i 1](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-34.jpg)
Knot Homologies • Khovanov homology: [M. Khovanov] Example: 3 2 1 0 i 1 3 5 7 9 j
![Knot Homologies slN knot homology N3 foams web cobordisms M Khovanov N2 matrix Knot Homologies • sl(N) knot homology: N=3: “foams” (web cobordisms) [M. Khovanov] N>2: matrix](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-35.jpg)
Knot Homologies • sl(N) knot homology: N=3: “foams” (web cobordisms) [M. Khovanov] N>2: matrix factorizations [M. Khovanov, L. Rozansky]

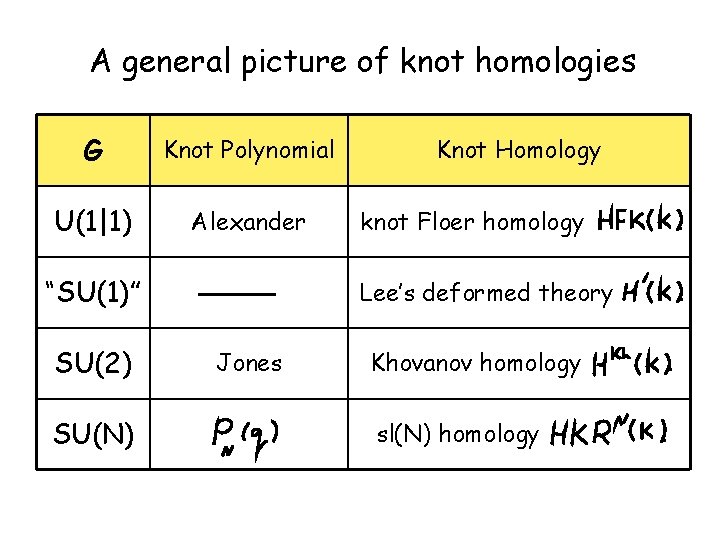
A general picture of knot homologies G Knot Polynomial U(1|1) Alexander “SU(1)” SU(2) SU(N) Jones Knot Homology knot Floer homology . Lee’s deformed theory . Khovanov homology . sl(N) homology .

sl(N) knot homology • is a functor (from knots and cobordisms to bigraded abelian groups and homomorphisms) • is stronger than • is hard to compute (only sl(2) up to … crossings) • cries out for a physical interpretation!

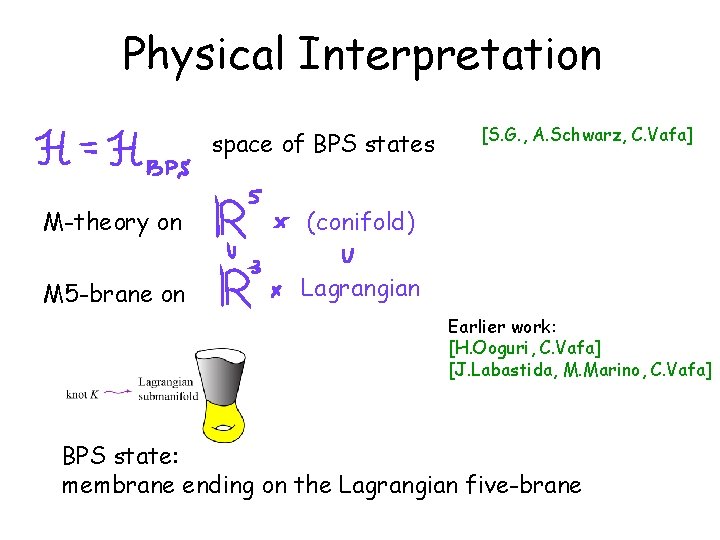
Physical Interpretation space of BPS states M-theory on (conifold) M 5 -brane on Lagrangian [S. G. , A. Schwarz, C. Vafa] Earlier work: [H. Ooguri, C. Vafa] [J. Labastida, M. Marino, C. Vafa] BPS state: membrane ending on the Lagrangian five-brane

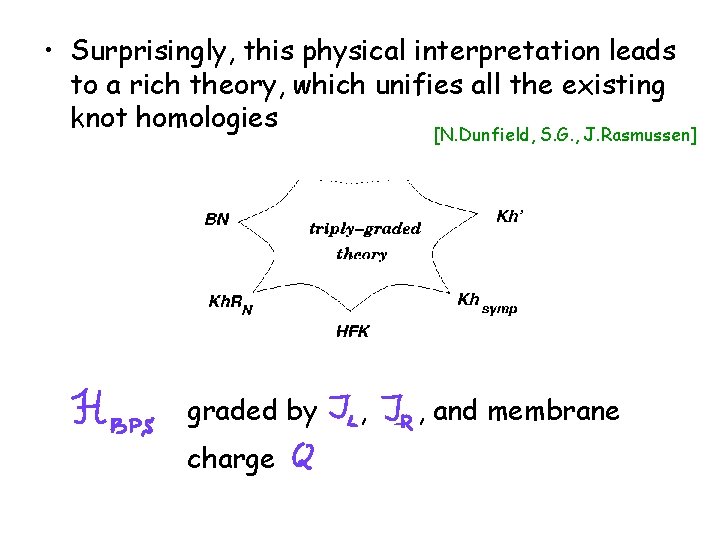
• Surprisingly, this physical interpretation leads to a rich theory, which unifies all the existing knot homologies [N. Dunfield, S. G. , J. Rasmussen] graded by charge , , and membrane



Families of Differentials • differentials • cohomology sl(N) knot homology N>2 Lee’s theory N=1 knot Floer homology N=0

Matrix Factorizations, Deformations, and Differentials

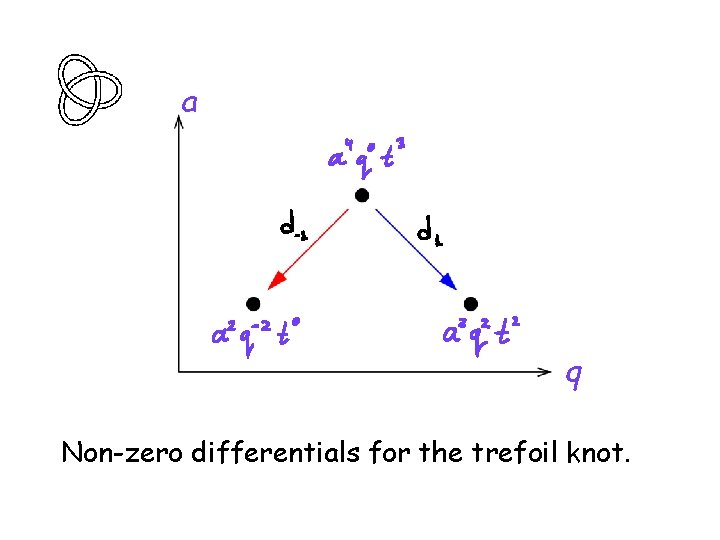
a q Non-zero differentials for the trefoil knot.

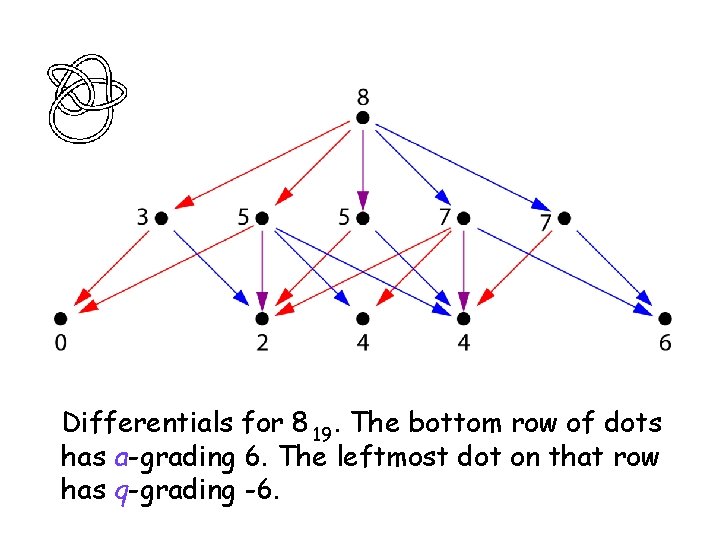
Differentials for 8 19. The bottom row of dots has a-grading 6. The leftmost dot on that row has q-grading -6.

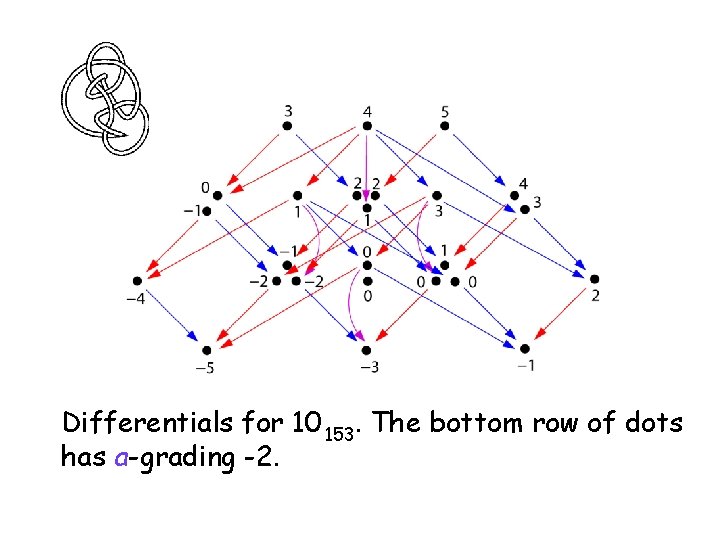
Differentials for 10 153. The bottom row of dots has a-grading -2.
![Whats Next Generalization to other groups and representations S G J Walcher What’s Next? • Generalization to other groups and representations [S. G. , J. Walcher]](https://slidetodoc.com/presentation_image_h/13749e021da0405c531413849bbaa296/image-47.jpg)
What’s Next? • Generalization to other groups and representations [S. G. , J. Walcher] • The role of matrix factorizations • Finite N (stringy exclusion principle) • Realization in topological gauge theory • Boundaries, corners, … • Surface operators • Braid group actions on D-branes

Gauge Theory and Categorification gauge theory on a 4 -manifold X number Z(X) (partition function)

Gauge Theory and Categorification gauge theory on a 4 -manifold X number Z(X) (partition function) gauge theory on = 3 -manifold vector space (Hilbert space)

Gauge Theory and Categorification gauge theory on a 4 -manifold X number Z(X) (partition function) gauge theory on = 3 -manifold vector space (Hilbert space) gauge theory on = surface category of branes (boundary conditions)

gauge theory on X self-duality equations: Z(X) counts solutions +…=0 gauge theory on monopole equations: FA + MM + … = 0 gauge theory on vortex equations: +…=0 =H( ) = moduli space topological A-model/B-model = Fuk b D

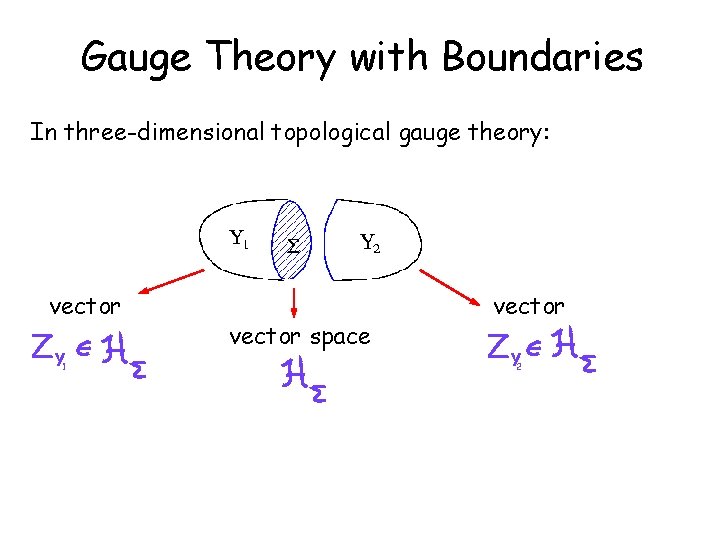
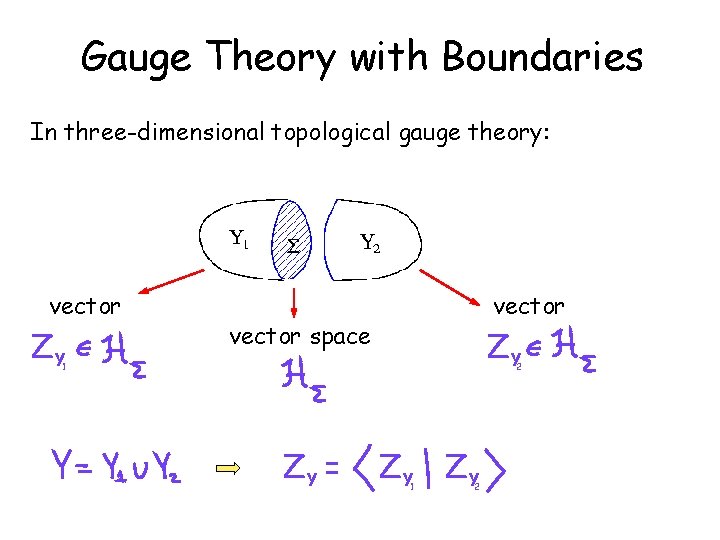
Gauge Theory with Boundaries In three-dimensional topological gauge theory: vector ZY 1 vector space vector ZY 2

Gauge Theory with Boundaries In three-dimensional topological gauge theory: vector ZY vector space ZY 2 1 ZY = ZY ZY 1 2

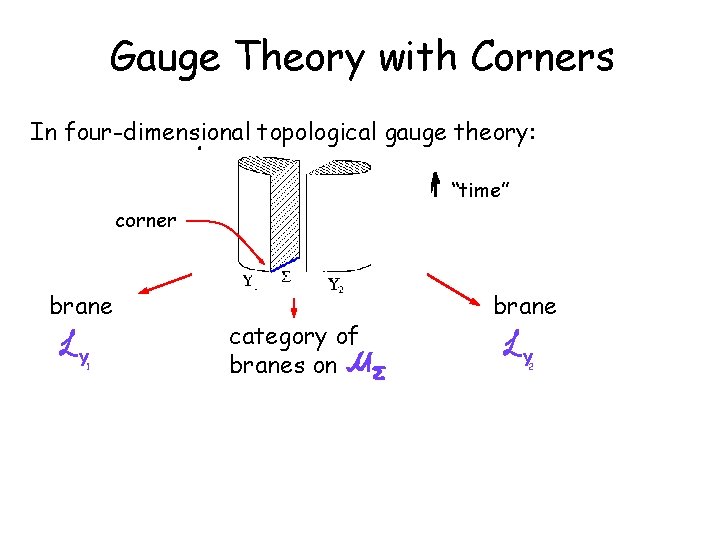
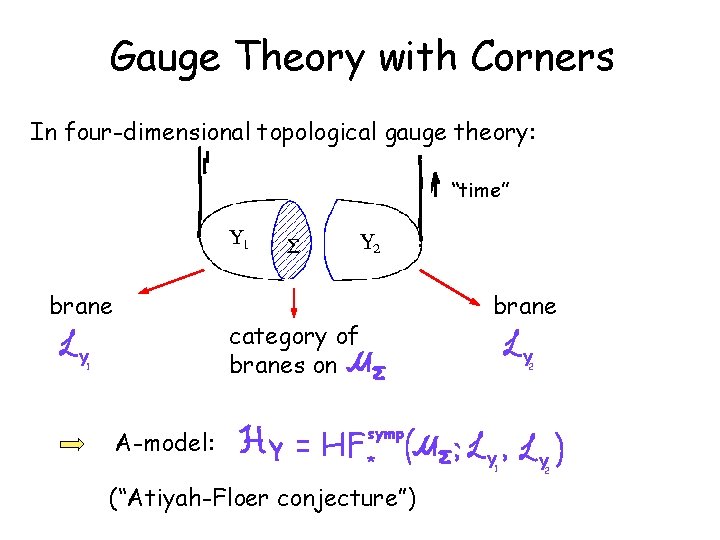
Gauge Theory with Corners In four-dimensional topological gauge theory: “time” corner brane Y 1 category of branes on brane Y 2

Gauge Theory with Corners In four-dimensional topological gauge theory: “time” brane category of branes on Y 1 A-model: Y 2 = HF * symp (“Atiyah-Floer conjecture”) Y 1 Y 2

From Lines to Surfaces • A line operator lifts to an operator in 4 D gauge theory localized on the surface S = where the gauge field A has a prescribed singularity Hol (A) C fixed conjugacy class in G

Braid Group Actions on D-branes • Any four-dimensional topological gauge theory which admits supersymmetric surface operators provides (new) examples of braid group actions on D-branes • Example: topological twist (GL twist) of N=4 super. Yang-Mills on with 4 surface operators =

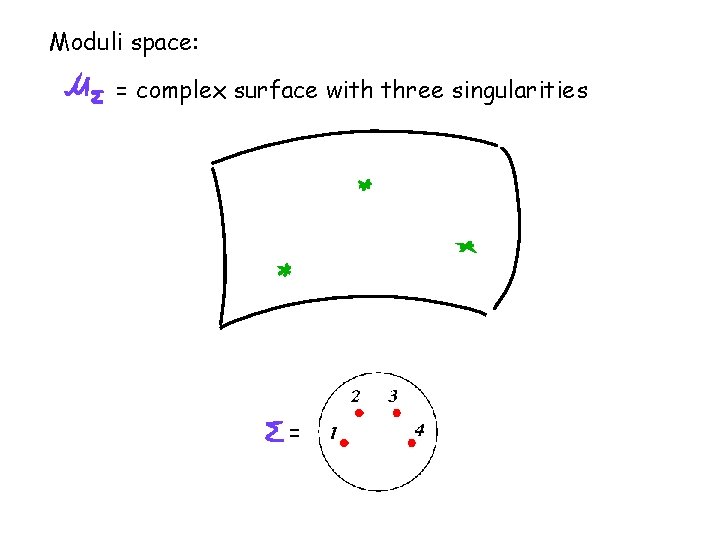
Moduli space: = complex surface with three singularities =

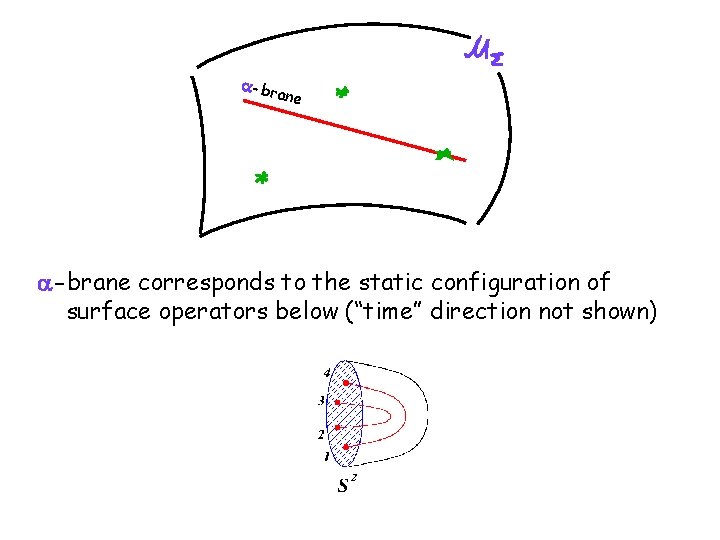
a-br ane a-brane corresponds to the static configuration of surface operators below (“time” direction not shown)

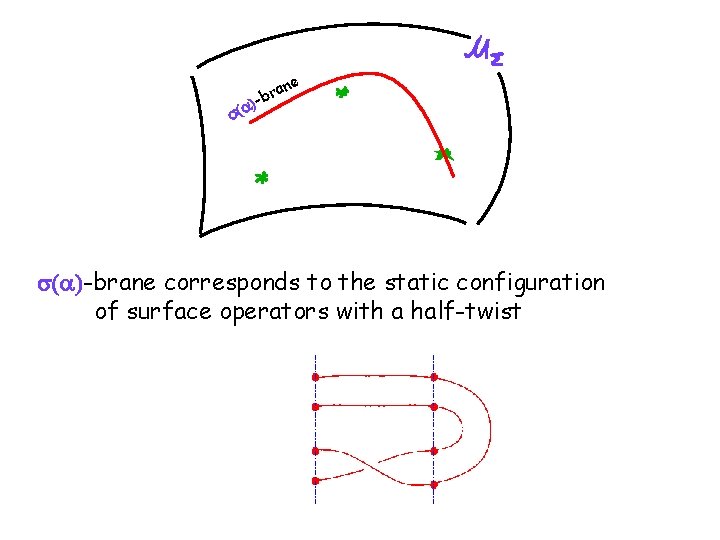
e s(a ) an r b - s(a)-brane corresponds to the static configuration of surface operators with a half-twist

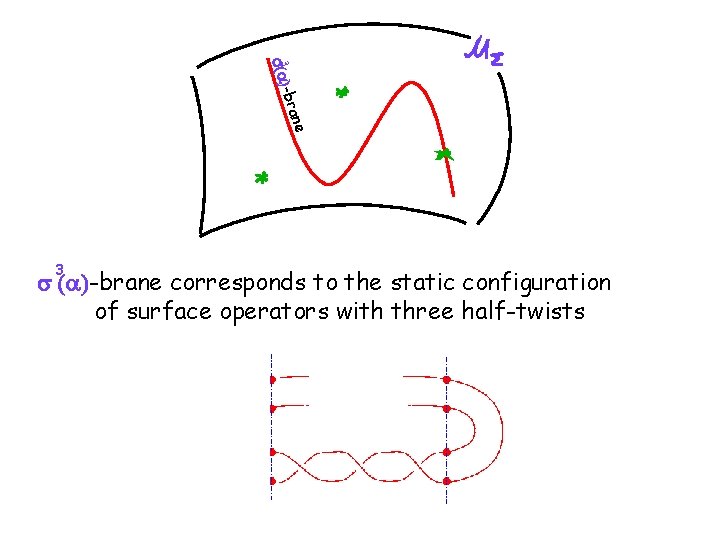
e bran 3 s(a) 3 s (a)-brane corresponds to the static configuration of surface operators with three half-twists

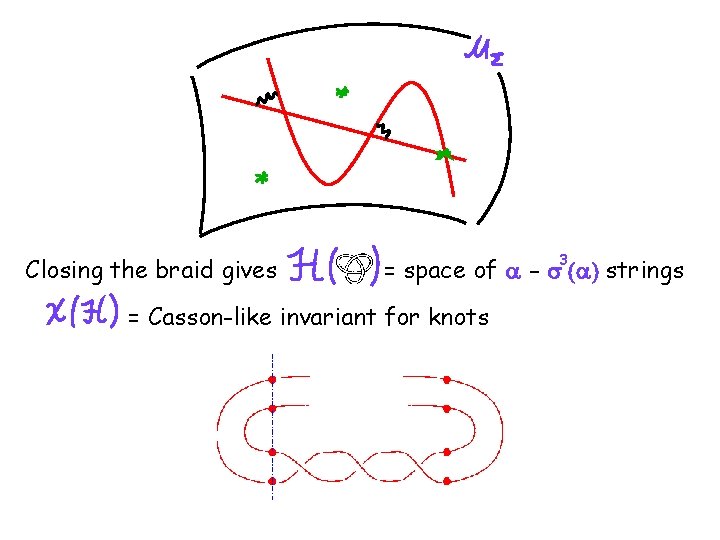
Closing the braid gives 3 = space of a - s (a) strings = Casson-like invariant for knots
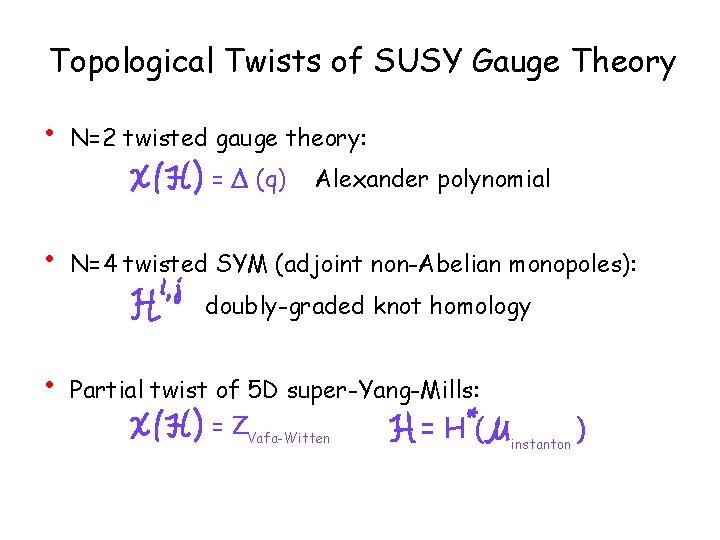
Topological Twists of SUSY Gauge Theory • N=2 twisted gauge theory: = D (q) • Alexander polynomial N=4 twisted SYM (adjoint non-Abelian monopoles): doubly-graded knot homology • Partial twist of 5 D super-Yang-Mills: = ZVafa-Witten =H( instanton )


 Sergei gukov
Sergei gukov Boatmans hitch
Boatmans hitch What does the theory of evolution state
What does the theory of evolution state Developmental homologies
Developmental homologies Developmental homologies
Developmental homologies Homologies
Homologies Homologies
Homologies Sergei sedov
Sergei sedov Philippe denain monaco
Philippe denain monaco Lennot jekaterinburg bryssel
Lennot jekaterinburg bryssel Sergei nagaitsev
Sergei nagaitsev Francys arsentiev sergei arsentiev
Francys arsentiev sergei arsentiev Sergei gepshtein
Sergei gepshtein What of this goldfish would you wish theme about happiness
What of this goldfish would you wish theme about happiness Sergei komarov contact info
Sergei komarov contact info Sergei korolev
Sergei korolev Flavorful sentence
Flavorful sentence Topological sort pseudocode
Topological sort pseudocode Topological sorting definition
Topological sorting definition Topological sort calculator
Topological sort calculator Topological sort calculator
Topological sort calculator Explain various boundary descriptors.
Explain various boundary descriptors. Boundary descriptors in digital image processing
Boundary descriptors in digital image processing Topological sort time complexity
Topological sort time complexity Topological mott insulator
Topological mott insulator Topological sort online
Topological sort online Dfs connected components
Dfs connected components Topological sort pseudocode
Topological sort pseudocode Topological sort
Topological sort Topological sort bfs
Topological sort bfs Difference between insertion sort and bubble sort
Difference between insertion sort and bubble sort Topological sort can be implemented by?
Topological sort can be implemented by? Graph topological sort
Graph topological sort Kahn's algorithm python
Kahn's algorithm python Topological sort algorithm
Topological sort algorithm Topological sort
Topological sort Partial order
Partial order Topological sorting
Topological sorting Topological sort演算法
Topological sort演算法 Topological band theory
Topological band theory Ceiiinosssttuu
Ceiiinosssttuu Pointers and strings
Pointers and strings Strings and other things
Strings and other things Come sleep o sleep
Come sleep o sleep Macam macam ikatan dan kegunaannya
Macam macam ikatan dan kegunaannya Arrow of light knot
Arrow of light knot Gordian knot allusion
Gordian knot allusion Josephine knot meaning
Josephine knot meaning Mythological allusion
Mythological allusion Bowline knot
Bowline knot Tiedid
Tiedid Square knot for restraints
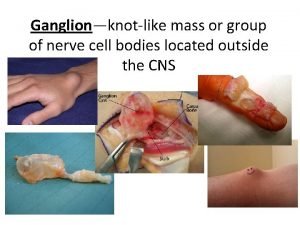
Square knot for restraints Knot like mass of nerve cell bodies
Knot like mass of nerve cell bodies Burning bush allusion
Burning bush allusion Anatomy
Anatomy Half boson knot
Half boson knot Ballie rüzgar gülü
Ballie rüzgar gülü Clove hitch restraint definition
Clove hitch restraint definition Viennese knot
Viennese knot What is a knot
What is a knot Dog menstrual cycle
Dog menstrual cycle Knots dog
Knots dog Knot tying ppt
Knot tying ppt Bell ringers knot
Bell ringers knot Double sheet bend
Double sheet bend Enamel parts
Enamel parts