Digital Image Processing Image descriptors Representation Description After

Digital Image Processing Image descriptors

Representation & Description • After Segmentation – We need to represent (or describe) the segmented region – Representation is used for further processing – Often desire a compact representation that describes the object itself – Can be used for comparison, selection, etc

Desirable properties of descriptors • Representations/Descriptions should be invariant: – Translation – Rotation – Scale • Similar regions should have the same description regardless of their position or orientation in the image

Representation Schemes • Generally two approaches • Boundary Characteristics – Represent region by external characteristics (ie, the boundary) • Region Characteristics – Represent region by internal characteristics

Boundary descriptors • Chain codes • Fourier descriptors • Others: – Polygonal Approximations – Signature

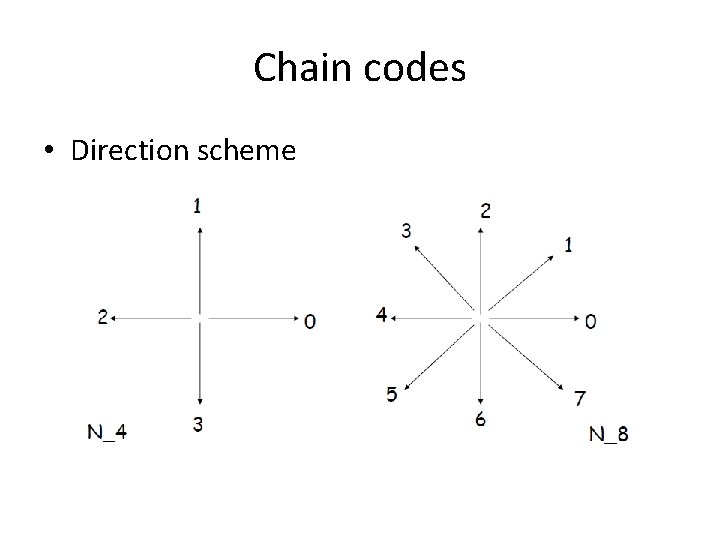
Chain Codes • Chain codes are used to represent a boundary – Uses a logically connected sequence of straight-line segments – The line segments specify direction • Direction coded using a number scheme Based on N_4 or N_8 connectivity

Chain codes • Direction scheme

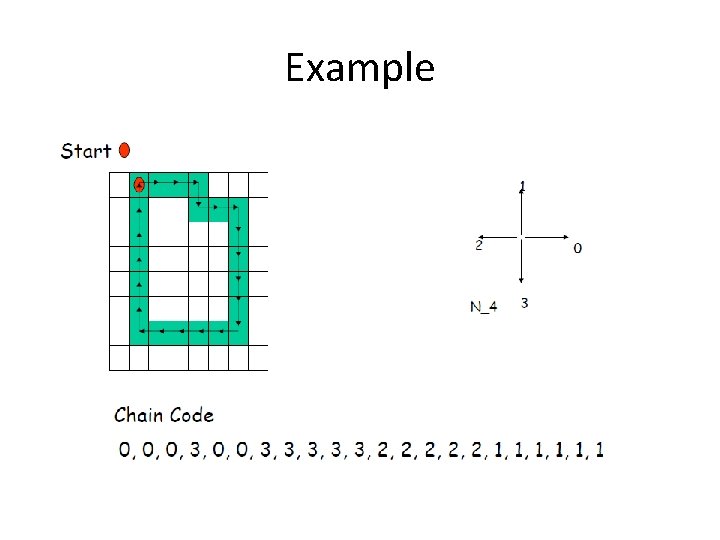
Chain codes • Chain coding can be created by following a boundary in some direction (say clockwise) assigning a direction to the segments connecting every pair of pixels (assumes a 1 pixel wide boundary)

Example

Chain Codes • Translation invariant – Note that this is different than a chain of (x, y) Coordinates. We are encoding the boundary itself. • Codes are sensitive to noise. If your boundary has some noise, this will show up in the chain code • One solution is Resample using a larger grid spacing. Also provides a more compact representation • Not scale invariant. You can provide several chain codes of the same bject at difference “resolutions”

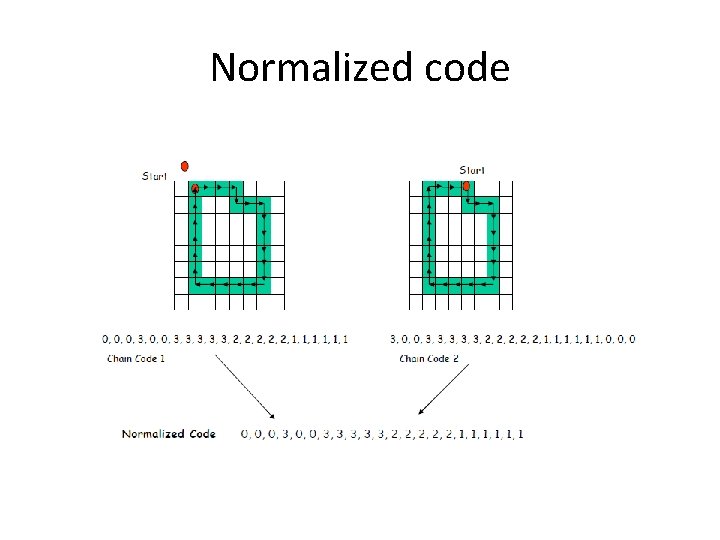
Chain codes • Chain Code depends on the starting point • We can normalize the chain code to address this problem – Assume the chain is a circular sequence – Redefine the starting point such that we generate an integer of smallest magnitude

Normalized code

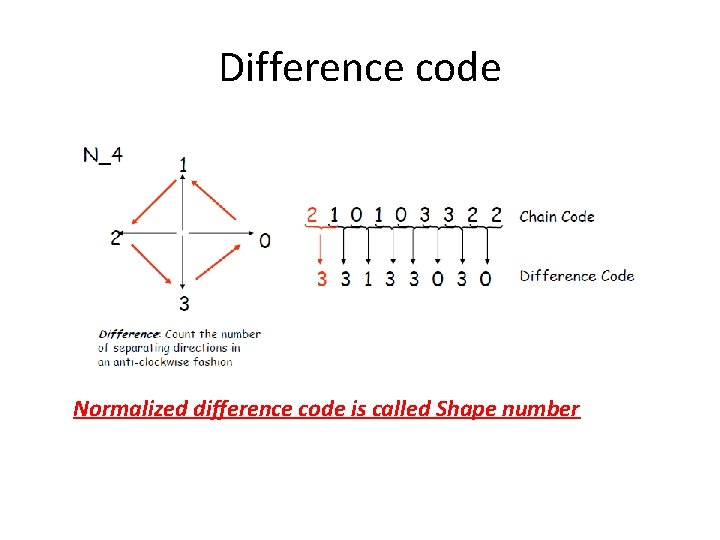
Chain Codes • Chain code depends on orientation – a rotation results in a different chain code • One solution is : Use the “first difference” of the chain code instead of the code itself • The difference is obtained by simply counting (counter-clockwise) the number of directions that separate two adjacent elements

Difference code Normalized difference code is called Shape number

Fourier Descriptors • Consider an N-point digital boundary in the x-y plane • This forms a coordinate pairs (xo, yo), (x 1, y 2), . . , (xn-1, yn-1) • We can consider this as two vectors x(k) = xk y(k) = yk • Furthermore – We could consider this a complex number – s(k) = x(k) + jy(k) where j=sqrt(-1)

Fourier Descriptors • Using the vector s(k) • Compute the 1 -D Discrete Fourier Transform • a(u) is called the Fourier Descriptors of the region • Note, that we can compute our original s(k) by:

Fourier Descriptors • Suppose, that instead of using all the a(u)’s, only • the first M coefficients are used. This is equivalent to setting a(u) = 0 for u > M. • This is a more compact representation • This procedure is also similar to a low-pass filter.

Fourier Descriptors • We only need a few descriptors to capture the gross shape of the boundary • We can compare low-order coefficients between shapes to see how similar they are.

Regional Descriptors • Area of the region – Number of pixels in the region • Perimeter – Length of its boundary • Compactness – (perimeter 2)/area – Compactness is invariant to translation, rotation, and scale

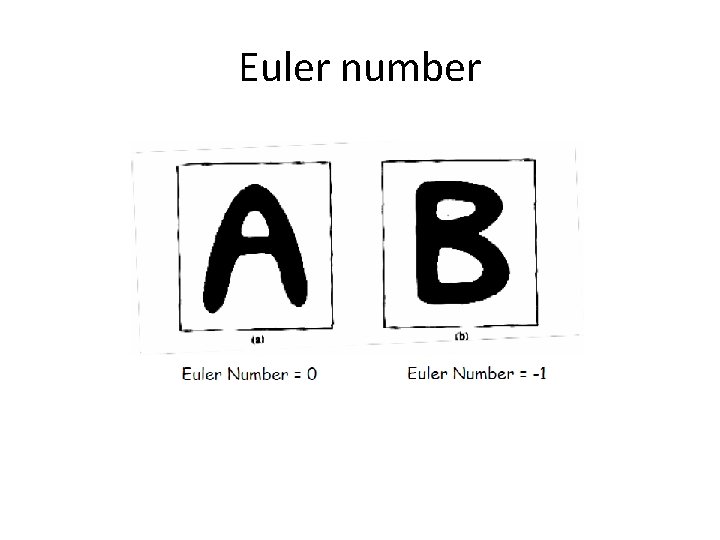
Regional Descriptors : Topological Descriptors • Topology is the study of properties of a figure that are unaffected by any deformation • Count the connected components in a region • Euler number, E, is a nice descriptor E = C –H – where C is the number of connected components – H is the number of holes

Euler number

Regional Descriptors: Moments • Moments are a certain weighted function of the image pixels' intensities usually chosen to have a geometric property or interpretation of a region. • For example, Geometric moments of low orders have an intuitive meaning – m 00 is a ”mass” of the image (for binary images, m 00 is an area of the object), m 10/m 00 and m 01/m 00 define the center of gravity or centroid of the image. Second -order moments m 20 and m 02 describe the ”distribution of mass” of the image with respect to the coordinate axes…. And so on.

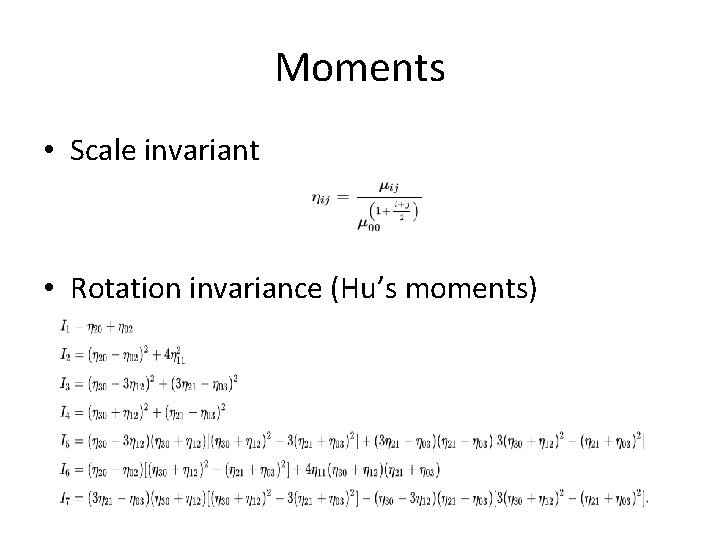
Regional Descriptors: Moments • Basic Moments • Moment invariants are special functions of image moments. • Translation invariant (Central moments)

Moments • Scale invariant • Rotation invariance (Hu’s moments)

Regional Descriptors: Texture-based descriptors • Texture is a basic visual cue, helping the human visual system in segmentation and recognition tasks. Its usage in computer vision has been a very active topic in the past three decades. • Texture is defined in dictionary as ”the characteristic appearance of a surface having a tactile quality”. However, in computer vision, there is no universally accepted definition for texture • A texture is not specified by the intensity (or color) in a single point. Therefore, texture descriptors are always based on some neighborhood. It is common to characterize the texture using a vector of scalar descriptors, which may be simply gray levels in some neighborhood or responses of different filters

Gabor filters • A set of Gabor filters with different frequencies and orientations may be helpful for extracting useful features from an image. In the discrete domain, twodimensional Gabor filters are given by, • where B and C are normalizing factors to be determined. f defines the frequency being looked for in the texture. By varying θ, we can look for texture oriented in a particular direction. By varying σ, we change the size of the image region being analyzed.

Gabor Transform • The Gabor transform of an image R(x, y) is defined as the convolution of a Gabor filter g(x, y) with image I(x, y) : • where * denotes two-dimensional linear convolution and M and N are the size of the Gabor filter mask.

Gabor Transform The carrier is a complex sinusoid s(x, y) – (u 0, v 0) – the spatial frequency of the complex sinusoid, – Φ - the phase of the complex sinusoid, The envelope is a Gaussian function w(x, y) • • • K – scales the magnitude of the Gaussian envelope, x, y – scaling parameters of the two axis of the Gaussian envelope, (x 0, y 0) – the peak of the Gaussian function

Regional Descriptors: Scale-invariant feature transform

SIFT Algorithm • Image content is transformed into local feature coordinates that are invariant to translation, rotation, scale, partially invariant to illumination changes and robust to local geometric distortion. 1. Scale-space Extrema Detection. 2. Keypoint Localization. 3. Orientation Assignment 4. Keypoint Descriptor.

Scale-space Extrema Detection. • Scale-space filtering achieved through calculating Laplacian of Gaussians (Lo. G) with varying σ values. Gaussian kernel with low σ gives high value for small corner while guassian kernel with high σ fits well for larger corner. • SIFT algorithm uses Difference of Gaussians which is an approximation of Lo. G but with less computational cost • Resulting images are then searched for local extrema over different scales.

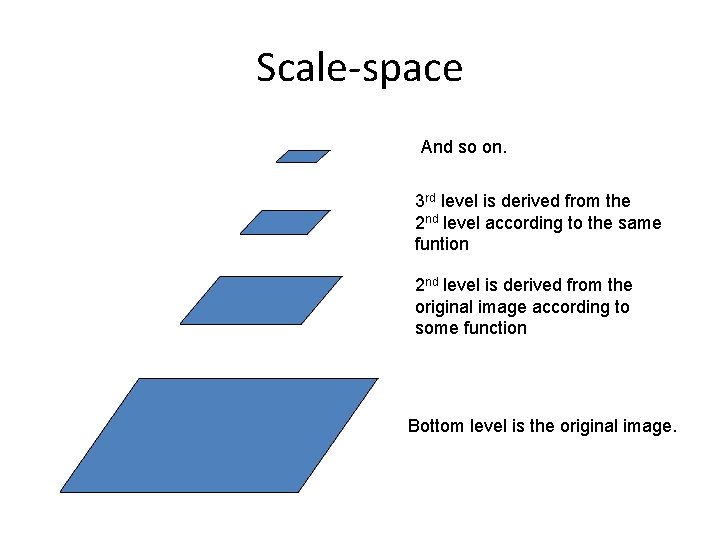
Scale-space And so on. 3 rd level is derived from the 2 nd level according to the same funtion 2 nd level is derived from the original image according to some function Bottom level is the original image.

Keypoint Localization • Once potential keypoints locations are found, they have to be refined to get more accurate results. So it eliminates any low-contrast keypoints and edge keypoints and what remains is strong interest points. • The algorithm performs a detailed fit to nearby data to determine the exact – location, scale, and ratio of principal curvatures

Orientation Assignment • Now an orientation is assigned to each keypoint to achieve invariance to image rotation. A neigbourhood is taken around the keypoint location at different scales, and the gradient magnitude and direction is calculated in that region. An orientation histogram with 36 bins covering 360 degrees is created. (It is weighted by gradient magnitude). The highest peak in the histogram is taken and any peak above 80% of it is also considered to calculate the orientation.

Keypoint descriptor • At this point, each keypoint has – location – scale – orientation • Next is to compute a descriptor for the local image region about each keypoint that is – highly distinctive – invariant as possible to variations such as changes in viewpoint and illumination

Keypoint descriptor • The local region (window) is normalized according to standard orientation and scale. • use the normalized region about the keypoint • compute gradient magnitude and orientation at each point in the region • weight them by a Gaussian window overlaid on the circle • create an orientation histogram over the 4 X 4 subregions of the window • 4 X 4 descriptors over 16 X 16 sample array were used in practice. 4 X 4 times 8 directions gives a vector of 128 values.