Topological Insulators Topological Semimetals and Quantum Hall Effects

Topological Insulators, Topological Semimetals, and Quantum Hall Effects without Landau Levels Kai Sun JQI-NSF-PFC and CMTC, University of Maryland, College Park

Outline Ø Introduction § Phenomena and theories of topological insulators § Realization in band insulators • Magnetic field/spin-orbit effects Ø Interaction induced topological states § 2 D integer topological states § 2 D fractional topological states § 3 D topological states

Collaborators 2 D Cold Gases Hong Yao (Berkeley) Eduardo Fradkin (UIUC) Steve Kivelson (Stanford) W. Vincent Liu (Pittsburgh) Andreas Hemmerich (Hamburg) Sankar Das Sarma (Maryland) 2 D Fractional Topological insulators Zhengcheng Gu (KITP, UCSB) Donna Sheng (California State) Hosho Katsura (Gakushuin University) Li Sheng (Nan. Jing) Sankar Das Sarma (Maryland) 3 D Elasticity in classical systems Maxim Dzero (Kent State) Victor Galitski(Maryland) Piers Coleman (Rutgers) Anton Souslov (Gatech) Xiaoming Mao (U Penn) Tom C. Lubensky (U Penn)

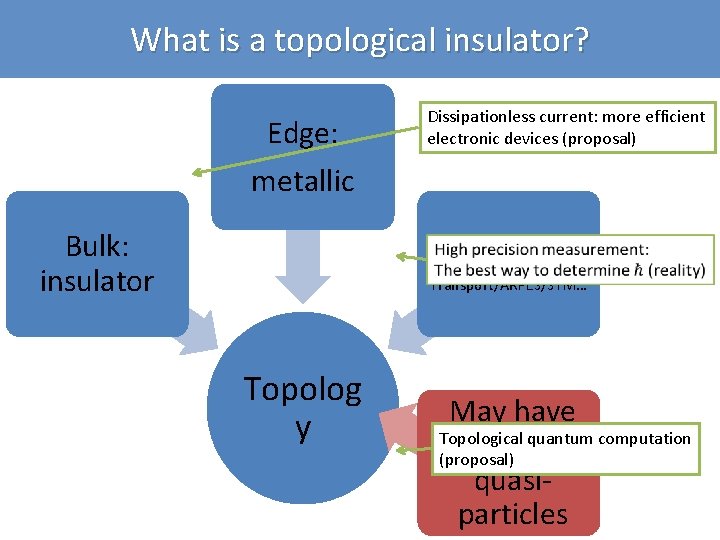
What is a topological insulator? Edge: metallic Bulk: insulator Dissipationless current: more efficient electronic devices (proposal) Quantization Transport/ARPES/STM… Topolog y May have Topological quantum computation fractional (proposal) quasiparticles

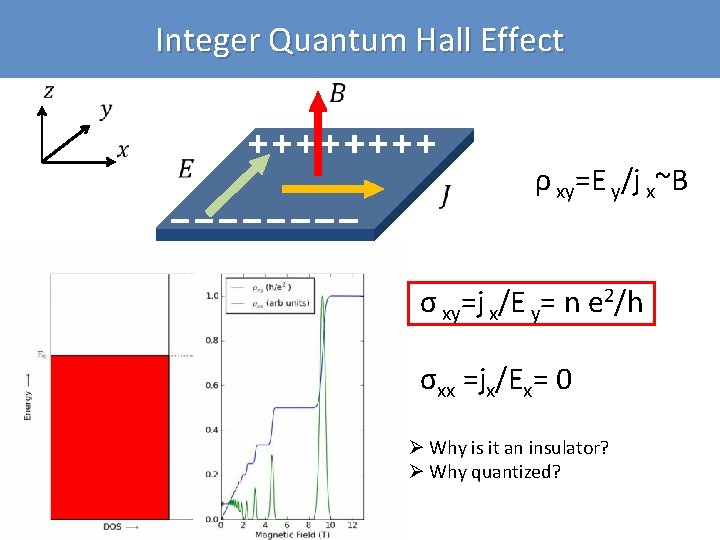
Integer Quantum Hall Effect ρ xy=E y/j x~B σ xy=j x/E y= n e 2/h σxx =jx/Ex= 0 Ø Why is it an insulator? Ø Why quantized?

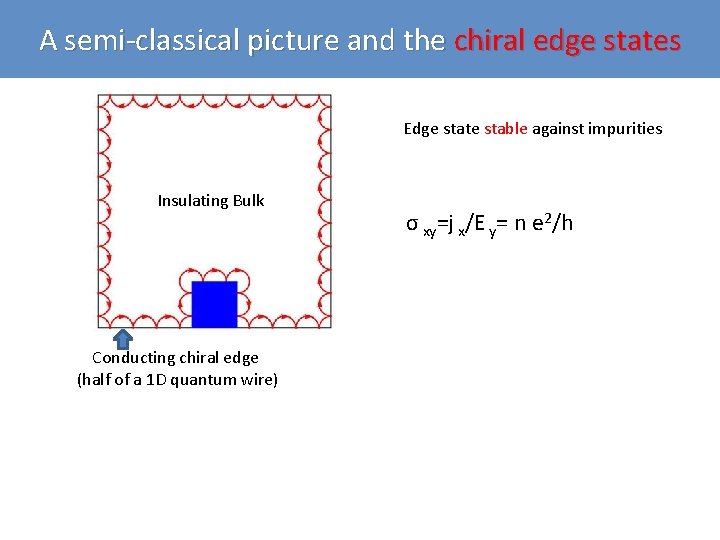
A semi-classical picture and the chiral edge states Edge state stable against impurities Insulating Bulk Conducting chiral edge (half of a 1 D quantum wire) σ xy=j x/E y= n e 2/h

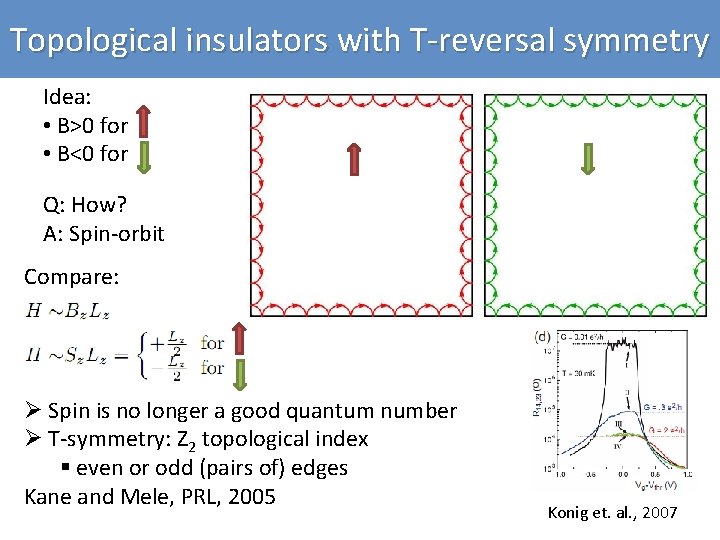
Topological insulators with T-reversal symmetry Idea: • B>0 for • B<0 for Q: How? A: Spin-orbit Compare: Ø Spin is no longer a good quantum number Ø T-symmetry: Z 2 topological index § even or odd (pairs of) edges Kane and Mele, PRL, 2005 Konig et. al. , 2007

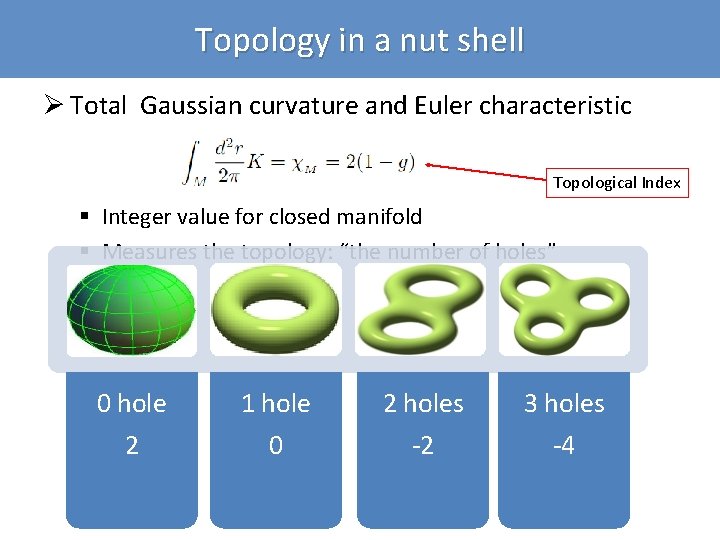
Topology in a nut shell Ø Total Gaussian curvature and Euler characteristic Topological Index § Integer value for closed manifold § Measures the topology: “the number of holes” 0 hole 1 hole 2 holes 3 holes 2 0 -2 -4

Topology in insulators Ø Total Berry curvature in the momentum space Bloch waves n is summed over fully occupied bands § First Chern number: Measures the topology of GS wave-function § Quantized (integer) for insulators § Ordinary Insulators: 0 § Each filled Landau level: 1 Topological insulator: Insulators with non-zero topological index • Other topological indices give other types of TIs.

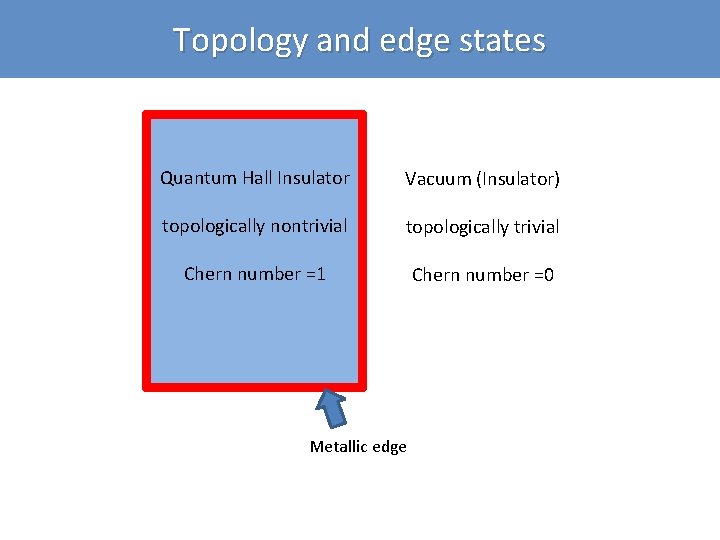
Topology and edge states Quantum Hall Insulator Vacuum (Insulator) topologically nontrivial topologically trivial Chern number =1 Chern number =0 Metallic edge

Rigorous Theory We need one “heavy” theoretical tool. Weight: 2. 9 pounds!

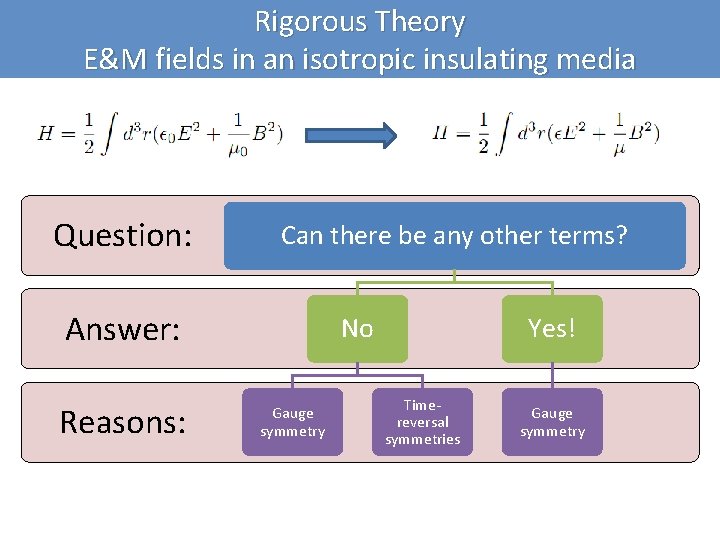
Rigorous Theory E&M fields in an isotropic insulating media Question: Can there be any other terms? Answer: Reasons: No Gauge symmetry Yes! Timereversal symmetries Gauge symmetry

Chern-Simons gauge theory A topological field theory: Ø k is quantized = the Chern number in IQHE Ø Open manifold: gauge invariant in the bulk but NOT on the edge good or bad? Cure from high-energy physics: gauge anomaly Ø 1 D chiral fermion also violates gauge symmetry Ø Two effects cancel each other, if there are k edges states Ø Gauge anomaly in (2 n-1) space dimensions and the Chern-Simons terms in 2 n space dimensions

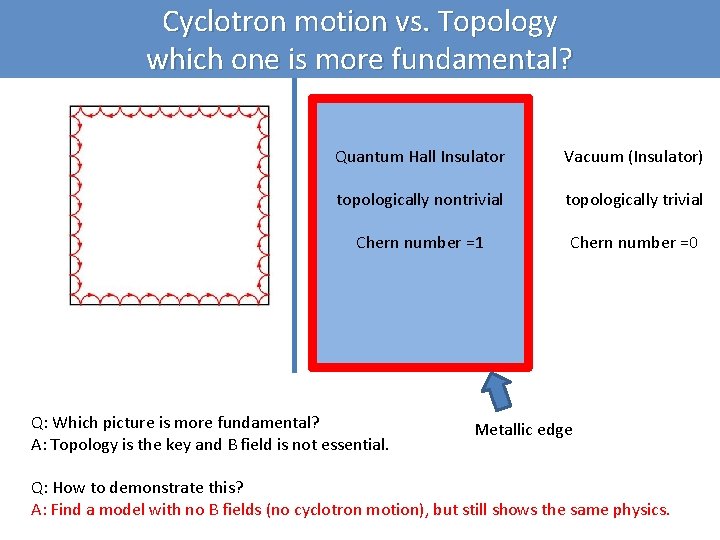
Cyclotron motion vs. Topology which one is more fundamental? Quantum Hall Insulator Vacuum (Insulator) topologically nontrivial topologically trivial Chern number =1 Chern number =0 Q: Which picture is more fundamental? A: Topology is the key and B field is not essential. Metallic edge Q: How to demonstrate this? A: Find a model with no B fields (no cyclotron motion), but still shows the same physics.

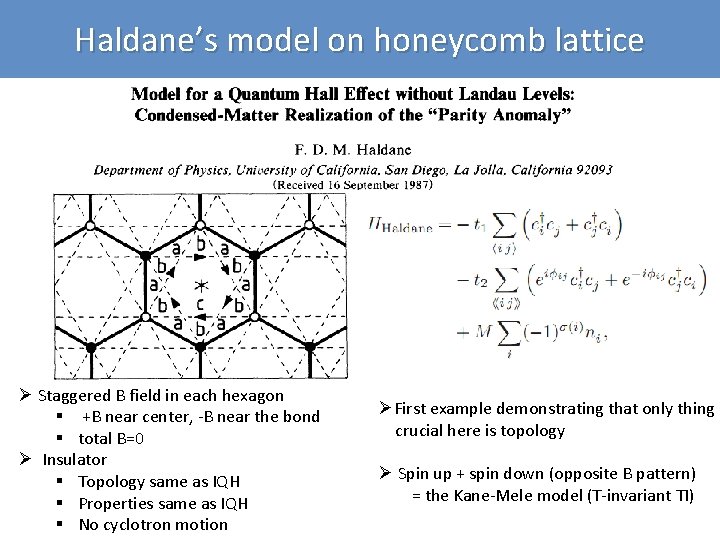
Haldane’s model on honeycomb lattice Ø Staggered B field in each hexagon § +B near center, -B near the bond § total B=0 Ø Insulator § Topology same as IQH § Properties same as IQH § No cyclotron motion ØFirst example demonstrating that only thing crucial here is topology Ø Spin up + spin down (opposite B pattern) = the Kane-Mele model (T-invariant TI)

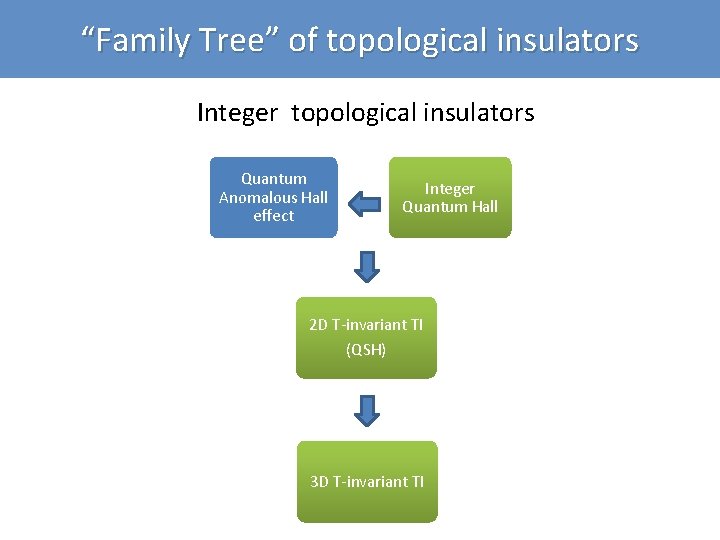
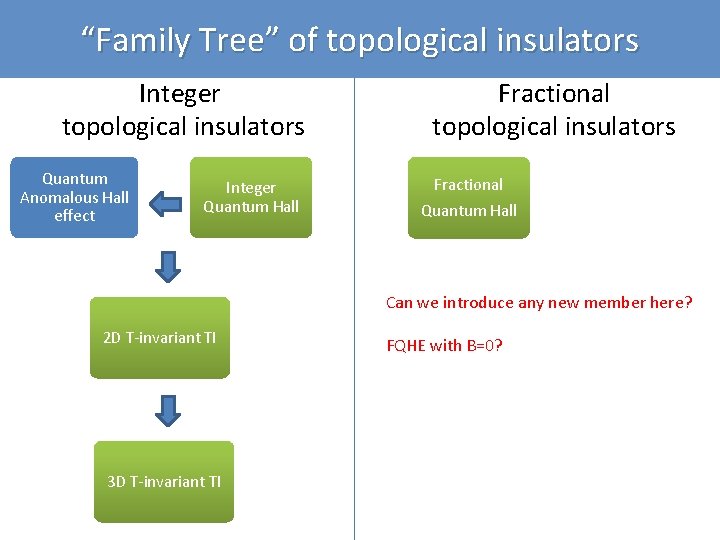
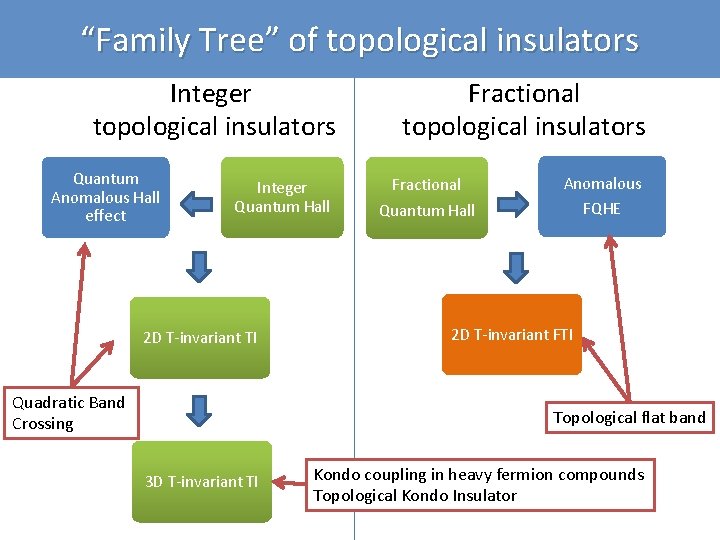
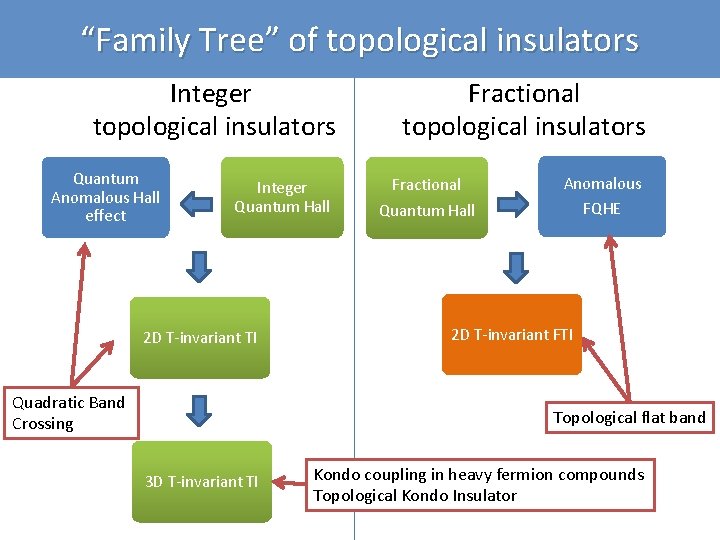
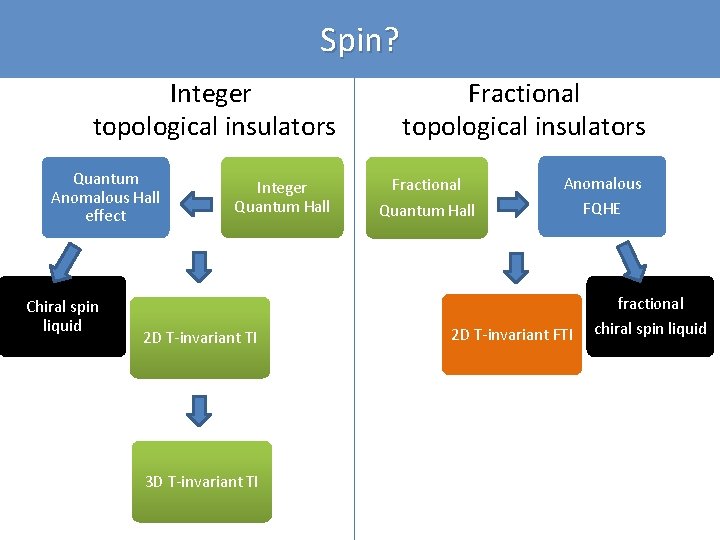
“Family Tree” of topological insulators Integer topological insulators Quantum Anomalous Hall effect Integer Quantum Hall 2 D T-invariant TI (QSH) 3 D T-invariant TI

Interactions induce TI? Ø All known TIs need B field/SO couplings Ø Q: Can TIs be stabilized without B-field or SO couplings? Focus: Interaction induced TIs without B or S-O couplings Why interactions? Ø History: free interactions § Noninteracting systems: well-understood § In the presence interactions: full of puzzles Ø Experiments § may reveal to us new families of topological materials.

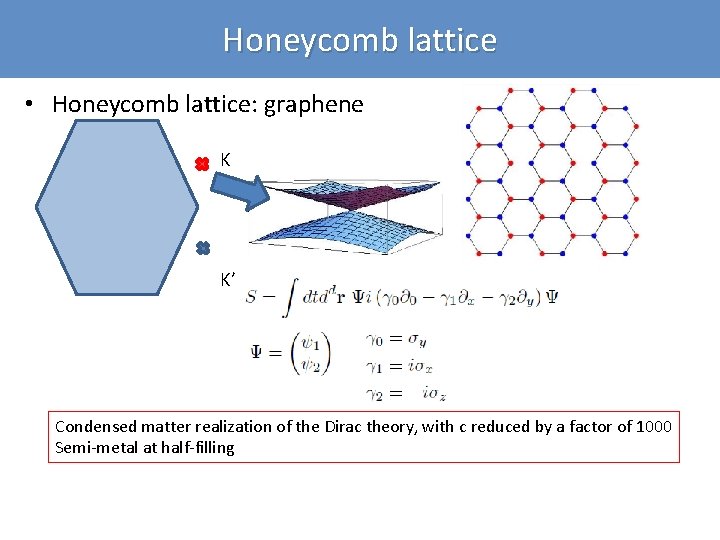
Honeycomb lattice • Honeycomb lattice: graphene K K’ Condensed matter realization of the Dirac theory, with c reduced by a factor of 1000 Semi-metal at half-filling

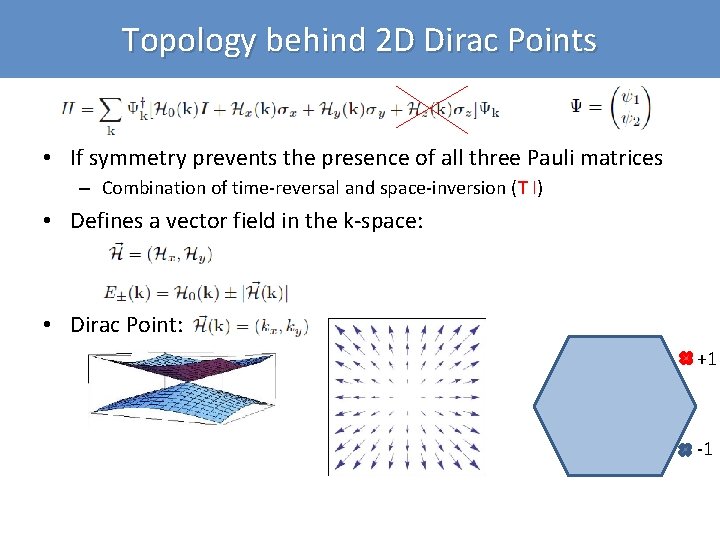
Topology behind 2 D Dirac Points • If symmetry prevents the presence of all three Pauli matrices – Combination of time-reversal and space-inversion (T I) • Defines a vector field in the k-space: • Dirac Point: +1 -1

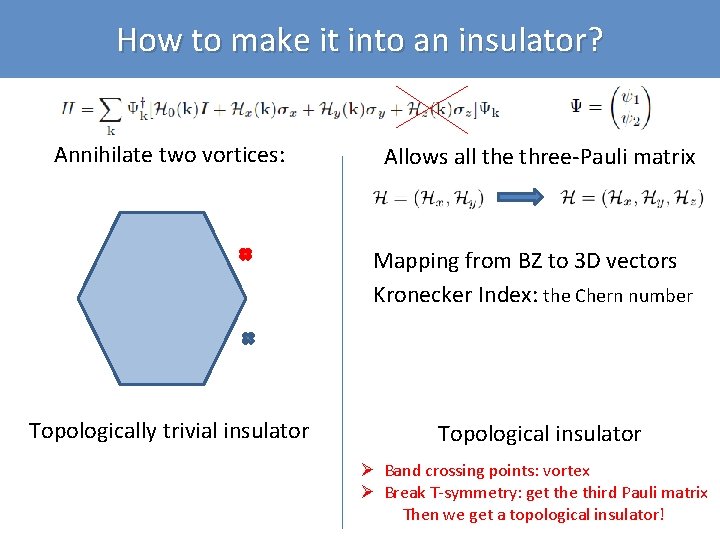
How to make it into an insulator? Annihilate two vortices: Allows all the three-Pauli matrix Mapping from BZ to 3 D vectors Kronecker Index: the Chern number Topologically trivial insulator Topological insulator Ø Band crossing points: vortex Ø Break T-symmetry: get the third Pauli matrix Then we get a topological insulator!

Interaction induce topological insulator without B? Graphene (Dirac point) is a bad choice • Dimension counting • g: irrelevant in d>1 • Weak coupling: Dirac points asymptotically free Kenneth G. winner Wilson Nobel Prize The Nobel Prize in Physics 1982 This is part of the renormalization group theory studies, which wins Wilson, PRD 7, 2911 (1973). him the prize • Strong coupling: Competing orders/uncontrollable o Hard to get: NNN repulsion> NN repulsion (Raghu, Qi, Honerkamp and Zhang, PRL, 2008). o Interaction destroys TI in Haldane’s model (Varney, KS, Rigol and Galitski, PRB, 2010).

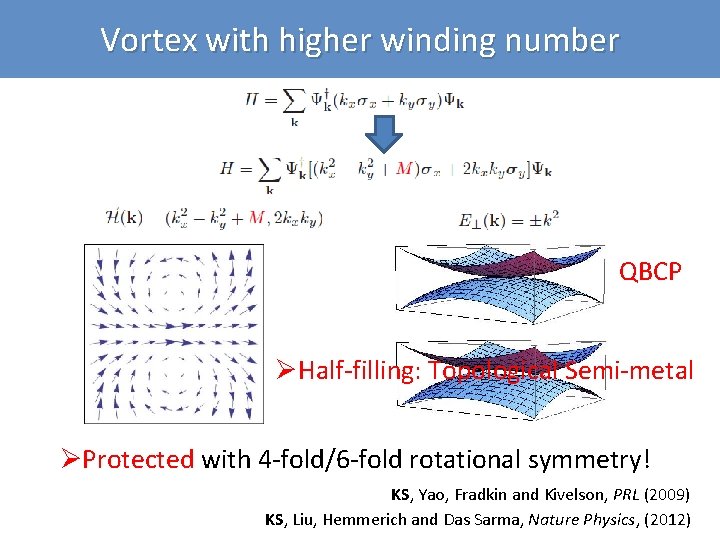
Vortex with higher winding number QBCP ØHalf-filling: Topological Semi-metal ØProtected with 4 -fold/6 -fold rotational symmetry! KS, Yao, Fradkin and Kivelson, PRL (2009) KS, Liu, Hemmerich and Das Sarma, Nature Physics, (2012)

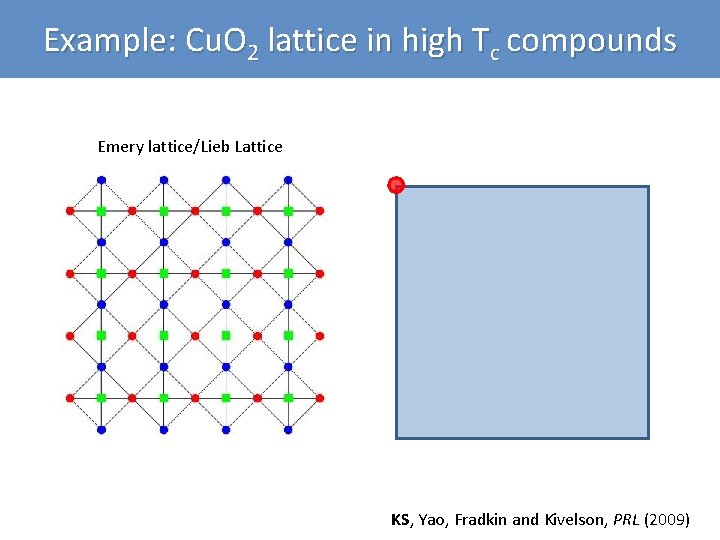
Example: Cu. O 2 lattice in high Tc compounds Emery lattice/Lieb Lattice KS, Yao, Fradkin and Kivelson, PRL (2009)

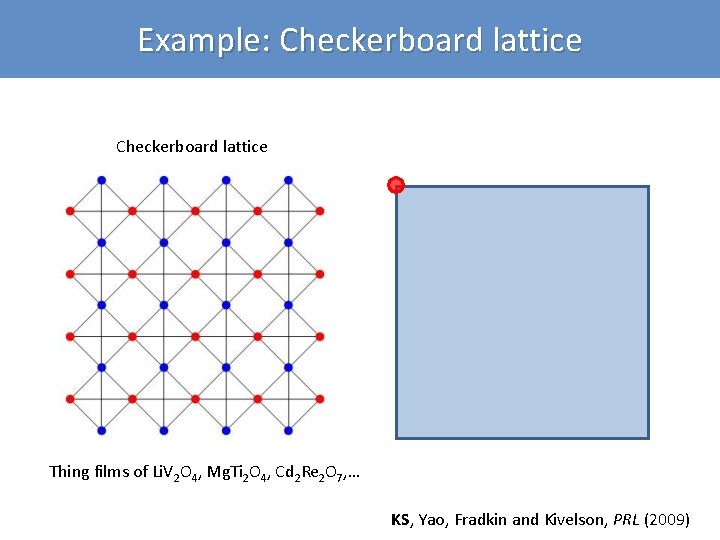
Example: Checkerboard lattice Thing films of Li. V 2 O 4, Mg. Ti 2 O 4, Cd 2 Re 2 O 7, … KS, Yao, Fradkin and Kivelson, PRL (2009)

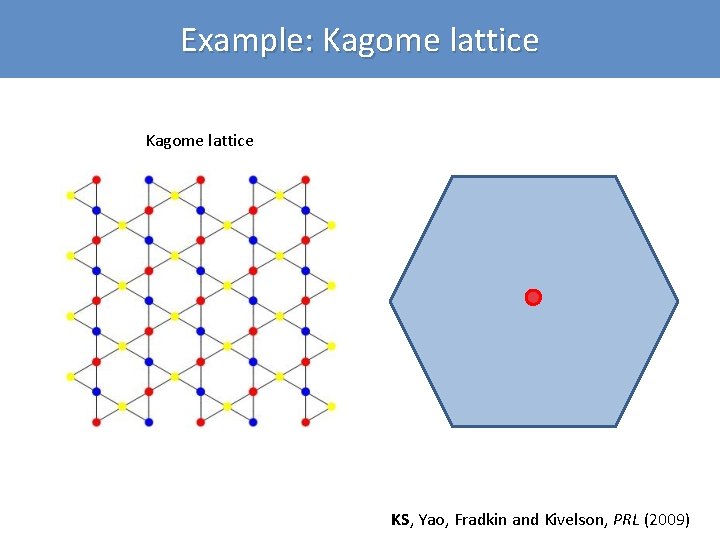
Example: Kagome lattice KS, Yao, Fradkin and Kivelson, PRL (2009)

Frustrated spin systems Topologically protected quadratic band crossing point in spinon spectrum C. Xu, F. Wang, Y. Qi, L. Balents and M. P. A. Fisher, 2011

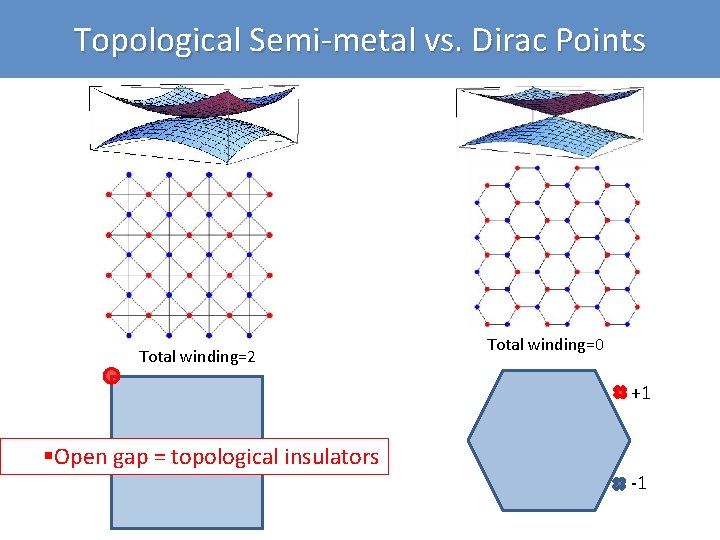
Topological Semi-metal vs. Dirac Points Total winding=2 Total winding=0 +1 , §Open gap = topological insulators -1

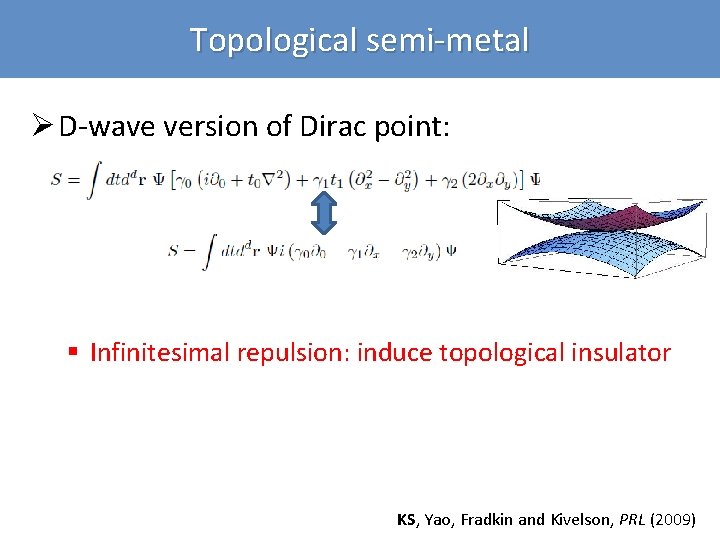
Topological semi-metal Ø D-wave version of Dirac point: § Infinitesimal repulsion: induce topological insulator KS, Yao, Fradkin and Kivelson, PRL (2009)

Interaction effect in topological semi-metals • Action: • Dimension counting • 2+1 D: RG flows for – t 0, t 1 , g and Ψ • t 0, t 1, and Ψ don’t flow at the one-loop level – doesn’t depend on momentum KS, Yao, Fradkin and Kivelson, PRL (2009)

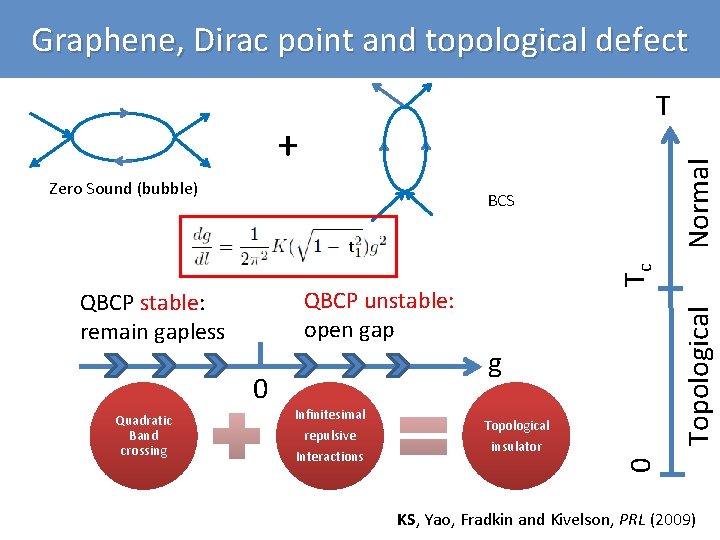
Graphene, Dirac point and topological defect + Zero Sound (bubble) Normal T BCS Topological QBCP unstable: open gap g 0 Infinitesimal repulsive Interactions Topological insulator 0 QBCP stable: remain gapless Quadratic Band crossing Tc t KS, Yao, Fradkin and Kivelson, PRL (2009)

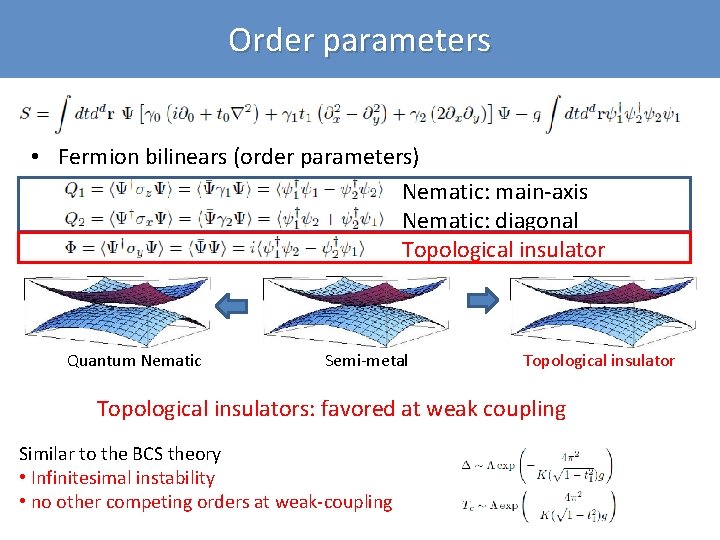
Order parameters • Fermion bilinears (order parameters) Nematic: main-axis Nematic: diagonal Topological insulator Quantum Nematic Semi-metal Topological insulators: favored at weak coupling Similar to the BCS theory • Infinitesimal instability • no other competing orders at weak-coupling

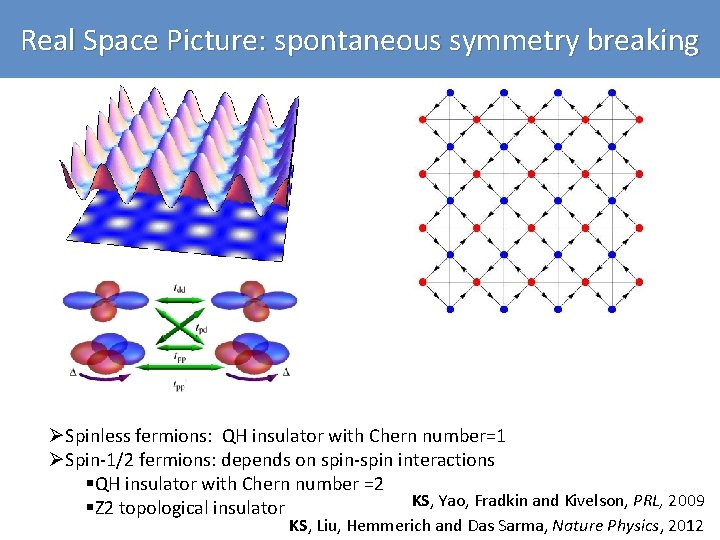
Real Space Picture: spontaneous symmetry breaking ØSpinless fermions: QH insulator with Chern number=1 ØSpin-1/2 fermions: depends on spin-spin interactions §QH insulator with Chern number =2 KS, Yao, Fradkin and Kivelson, PRL, 2009 §Z 2 topological insulator KS, Liu, Hemmerich and Das Sarma, Nature Physics, 2012

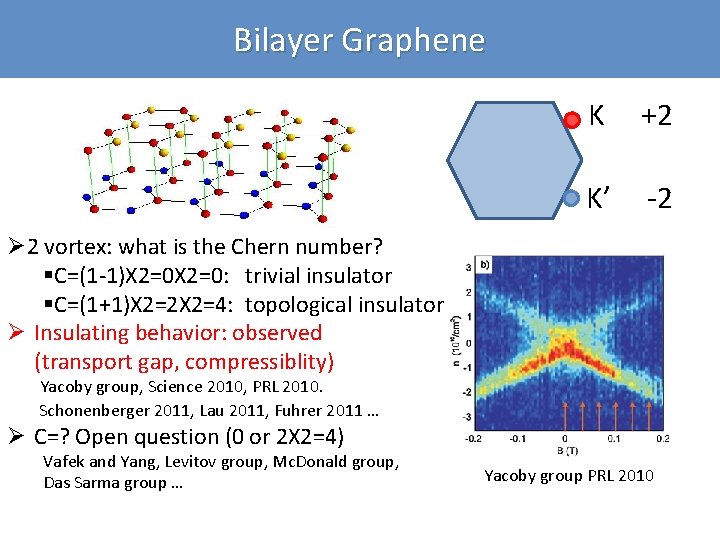
Bilayer Graphene K +2 K’ -2 Ø 2 vortex: what is the Chern number? §C=(1 -1)X 2=0: trivial insulator §C=(1+1)X 2=2 X 2=4: topological insulator Ø Insulating behavior: observed (transport gap, compressiblity) Yacoby group, Science 2010, PRL 2010. Schonenberger 2011, Lau 2011, Fuhrer 2011 … Ø C=? Open question (0 or 2 X 2=4) Vafek and Yang, Levitov group, Mc. Donald group, Das Sarma group … Yacoby group PRL 2010

TI in ultracold gases Topological insulators have never been achieved in cold gases! § Main Challenge: no B field and no spin-orbit coupling. § Possible solution #1: mimic B field (using rotations or laser beams) § Possible solution #2: TS + interactions =TI (without B or SO couplings) In cold gases, we can design the band structure and interactions! KS, Liu, Hemmerich and Das Sarma, Nature Physics, 2012

“Family Tree” of topological insulators Integer topological insulators Quantum Anomalous Hall effect Integer Quantum Hall 2 D T-invariant TI 3 D T-invariant TI Fractional topological insulators Fractional Quantum Hall

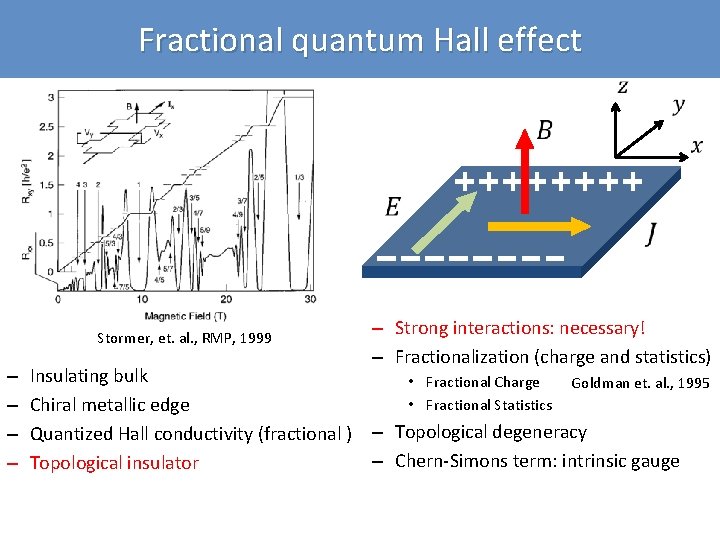
Fractional quantum Hall effect Stormer, et. al. , RMP, 1999 – – Insulating bulk Chiral metallic edge Quantized Hall conductivity (fractional ) Topological insulator – Strong interactions: necessary! – Fractionalization (charge and statistics) • Fractional Charge • Fractional Statistics Goldman et. al. , 1995 – Topological degeneracy – Chern-Simons term: intrinsic gauge

“Family Tree” of topological insulators Integer topological insulators Quantum Anomalous Hall effect Integer Quantum Hall Fractional topological insulators Fractional Quantum Hall Can we introduce any new member here? 2 D T-invariant TI 3 D T-invariant TI FQHE with B=0?

Why do we need a new setup for FQHE? • New FQH state

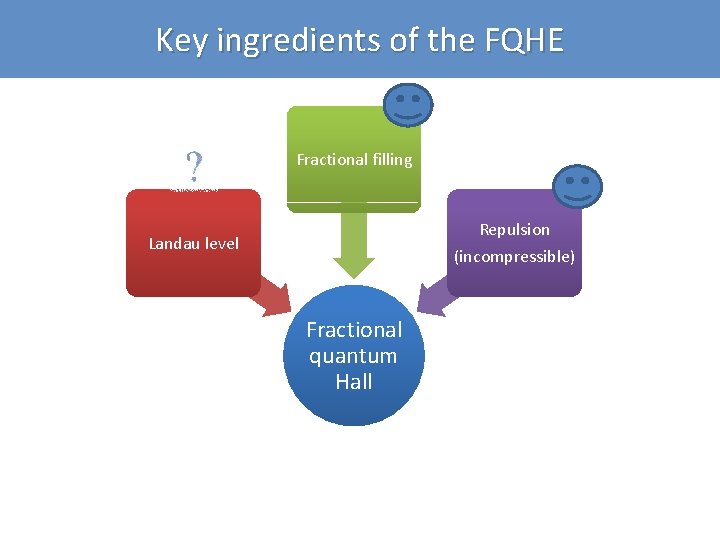
Key ingredients of the FQHE Fractional filling Repulsion (incompressible) Landau level Fractional quantum Hall

Landau level without B field? Nearly-flat band Nontrivial topological index Landau level 1. Start from a model with topological bands 2. Tune hopping strengths to reduce the bandwidth Topologically nontrivial nearly-flat bands • Checker-board lattice with NN, NNN and NNNN hoppings • Square lattice with NN hoppings • Kagome lattice with NN and NNN hoppings • Honeycomb lattice with NN and NNN hoppings • … Ø Hopping range ~ (gap/effective mass)1/2 Tang, et. al. , PRL (2011). KS, et. al. , PRL (2011). Neupert, et. al. , PRL (2011).

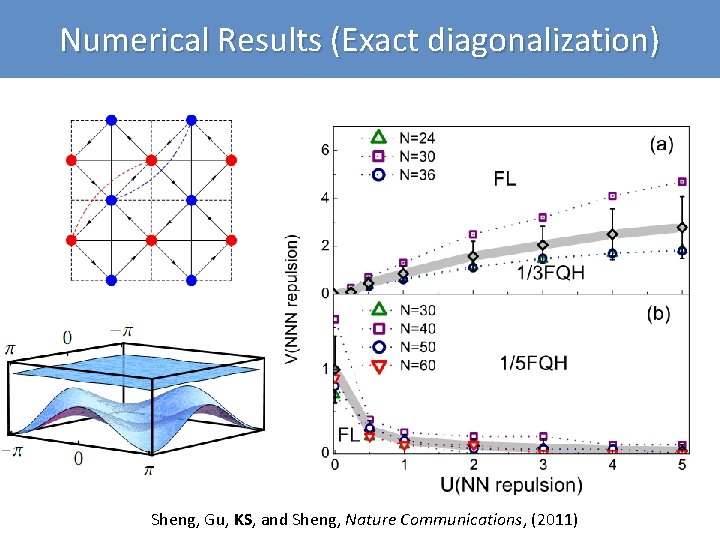
Numerical Results (Exact diagonalization) Sheng, Gu, KS, and Sheng, Nature Communications, (2011)

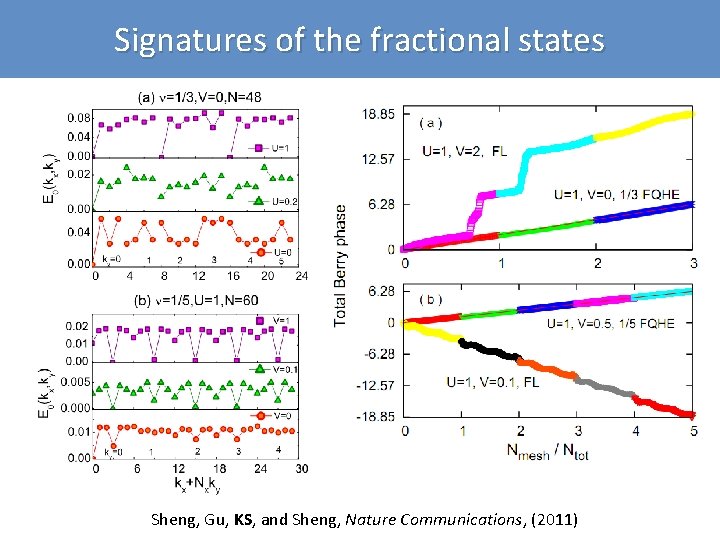
Signatures of the fractional states Sheng, Gu, KS, and Sheng, Nature Communications, (2011)

Knowledge and puzzles • Numerics: every topological property agrees with the FQHE – Topological degeneracy (KS, et. al, to be published) – Entanglement spectrum (Regnault, et. al. 2011, KS, et. al, to be published) – Abelian FQHE: fermion with odd denominator or bosons with even denominator (Wang, et. al. 2011) – Nonabelian FQHE: SU(2)k, with k+1 body interaction (Bernevig, et. al. , 2011) (TQC, universal TQC) • Theory: both progresses and puzzles – Girvin-Mac. Donald-Platzman algebra (Parameswaran et. al. 2011) – Wave-function on open cylinder/thin torus (Qi 2011) • no numerical confirmation yet – Composite fermions picture: not available • Mean-field: possible • Gauge fluctuations: no Chern-Simon’s gauge theory available on frustrated lattices yet – Parton: mean-field studies • no numerical confirmation yet • Gauge fluctuations: no Chern-Simon’s gauge theory available on frustrated lattices yet

Topological quantum computation FQHE in 2 DEG FQHE without B 3 D TI+SC Topological SC Well-studied Novel Bulk conductivity? Tuning? <1 K Up to room temperature <10 K <10 K Charged Neutral Majorana, Fibonacci, … Majorana only Universal TQC TQC

“Family Tree” of topological insulators Integer topological insulators Quantum Anomalous Hall effect Integer Quantum Hall 2 D T-invariant TI Quadratic Band Crossing Fractional topological insulators Fractional Quantum Hall Anomalous FQHE 2 D T-invariant FTI Topological flat band 3 D T-invariant TI Kondo coupling in heavy fermion compounds Topological Kondo Insulator

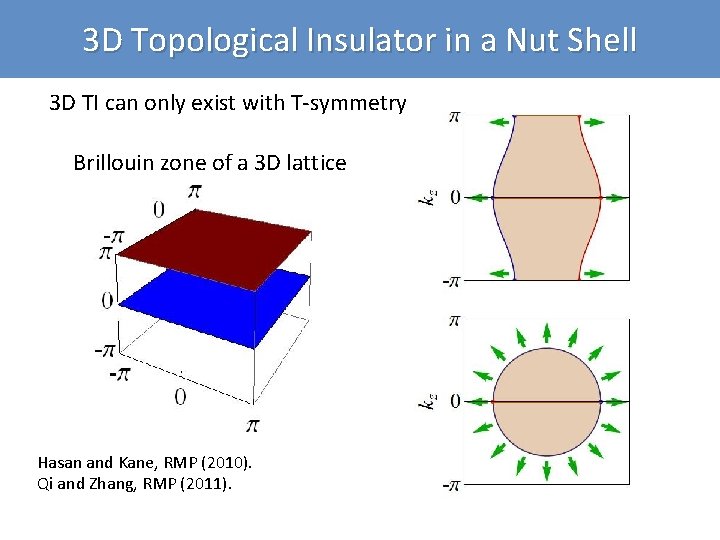
3 D Topological Insulator in a Nut Shell 3 D TI can only exist with T-symmetry Brillouin zone of a 3 D lattice Hasan and Kane, RMP (2010). Qi and Zhang, RMP (2011).

Heavy Fermion in a Nut Shell • Experimental signature: – Fermi liquid with very large effect electron mass ~ 100 me • Theoretical description: – Electrons moving on a lattice of local spins Dzero, KS, Galitski and Coleman, PRL, (2010).

Why topological? Topological Insulator and mass of a Dirac theory • Toy model of TI (X-L Qi, etc, PRB 2008) – TI: Dirac mass changes sign as k increases from 0 to ∞ – Conclusion remains if k is changed into odd function of k • Effective Hamiltonian of a Kondo insulator – Compare with model above To get a Topological insulator: – is an odd function of k and • Local spins and conducting electrons have opposite parities – “Dirac” mass changes sign Dzero, KS, Galitski and Coleman, PRL, (2010).

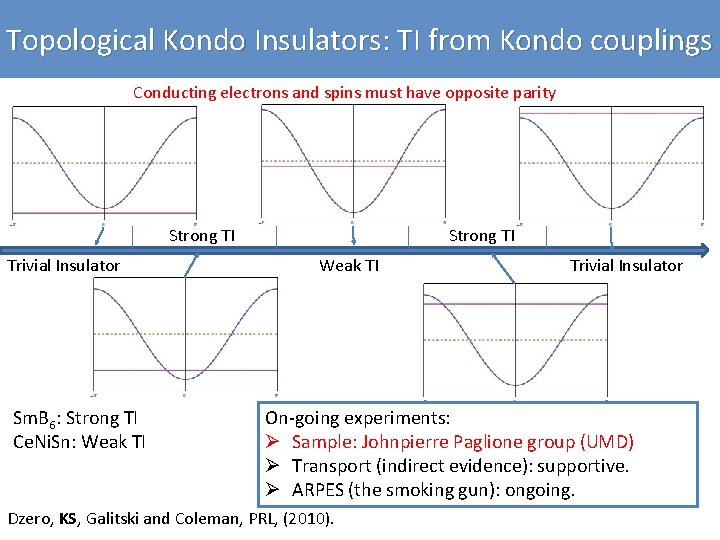
Topological Kondo Insulators: TI from Kondo couplings Conducting electrons and spins must have opposite parity Strong TI Trivial Insulator Sm. B 6: Strong TI Ce. Ni. Sn: Weak TI Strong TI Weak TI Trivial Insulator On-going experiments: Ø Sample: Johnpierre Paglione group (UMD) Ø Transport (indirect evidence): supportive. Ø ARPES (the smoking gun): ongoing. Dzero, KS, Galitski and Coleman, PRL, (2010).

“Family Tree” of topological insulators Integer topological insulators Quantum Anomalous Hall effect Integer Quantum Hall 2 D T-invariant TI Quadratic Band Crossing Fractional topological insulators Fractional Quantum Hall Anomalous FQHE 2 D T-invariant FTI Topological flat band 3 D T-invariant TI Kondo coupling in heavy fermion compounds Topological Kondo Insulator

Can we go even further? Can we use what we learned in TI to improve our understanding in other systems? Yes! Classical mechanics Frustrated spins

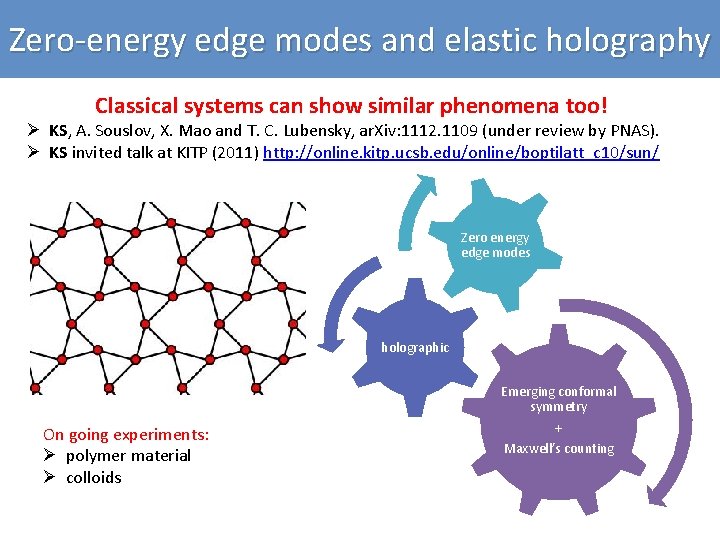
Zero-energy edge modes and elastic holography Classical systems can show similar phenomena too! Ø KS, A. Souslov, X. Mao and T. C. Lubensky, ar. Xiv: 1112. 1109 (under review by PNAS). Ø KS invited talk at KITP (2011) http: //online. kitp. ucsb. edu/online/boptilatt_c 10/sun/ Zero energy edge modes holographic Emerging conformal symmetry On going experiments: Ø polymer material Ø colloids + Maxwell’s counting

Spin? Integer topological insulators Quantum Anomalous Hall effect Chiral spin liquid Integer Quantum Hall 2 D T-invariant TI 3 D T-invariant TI Fractional topological insulators Fractional Quantum Hall Anomalous FQHE 2 D T-invariant FTI fractional chiral spin liquid

Collaborators 2 D 3 D Hong Yao (Berkeley) Eduardo Fradkin (UIUC) Steve Kivelson (Stanford) Maxim Dzero (Kent State) Victor Galitski(Maryland) Piers Coleman (Rutgers) Fractional Topological insulator Zhengcheng Gu (KITP, UCSB) Donna Sheng (California State) Hosho Katsura (Gakushuin University) Li Sheng (Nan. Jing) Sankar Das Sarma (Maryland) Cold Gases Elasticity in classical systems W. Vincent Liu (Pittsburgh) Andreas Hemmerich (Hamburg) Sankar Das Sarma (Maryland) Anton Souslov (Gatech) Xiaoming Mao (U Penn) Tom C. Lubensky (U Penn)