The Cover Time of Deterministic Random Walks for

The Cover Time of Deterministic Random Walks for General Transition Probabilities Takeharu Shiraga* *Kyushu University, Japan ※wikipedia

Network exploration by random walks n This work is corresponding to the network exploration by random walks and deterministic random walks n Random walks are well studied for an approach to the network exploration, since its simplicity, locality, and robustness to change in graphs. 2

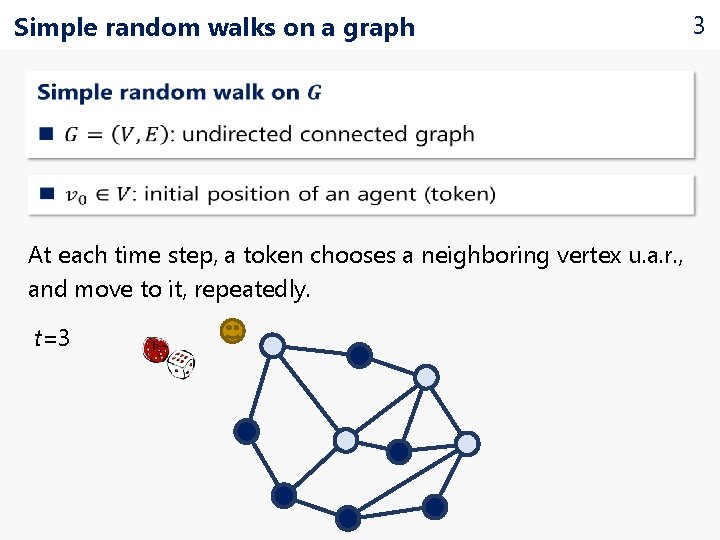
Simple random walks on a graph At each time step, a token chooses a neighboring vertex u. a. r. , and move to it, repeatedly. t=3 t=2 t=1 t=0 3

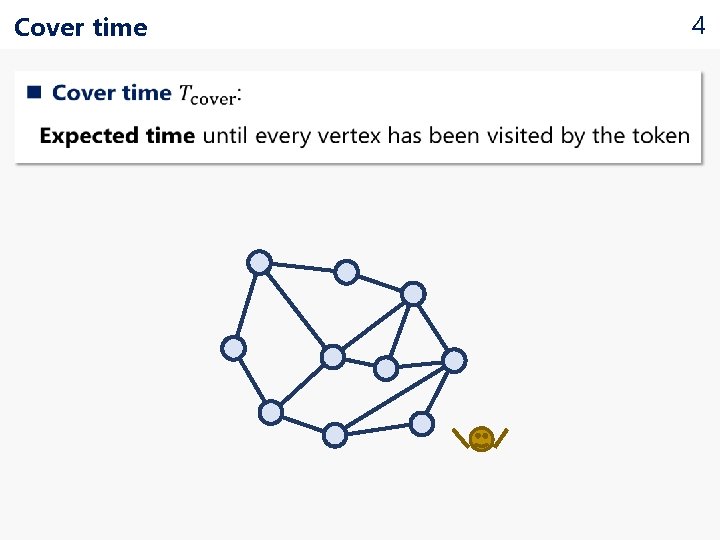
Cover time 4

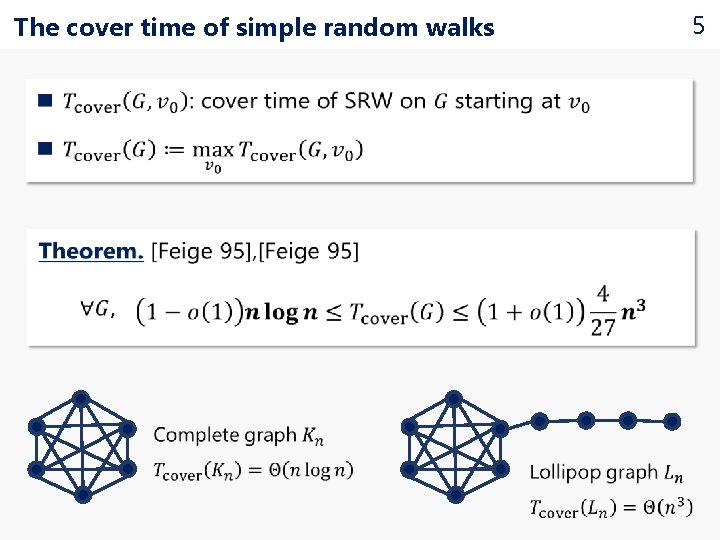
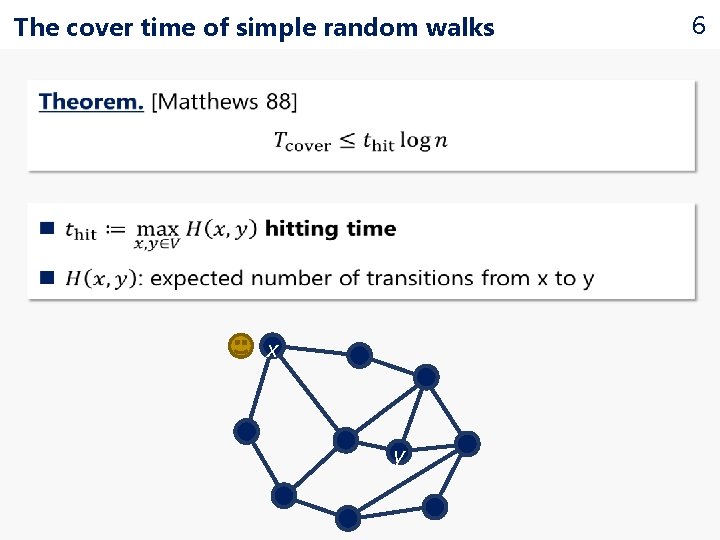
The cover time of simple random walks 5

The cover time of simple random walks x y 6

Summary (so far) Simple RW k=1 7

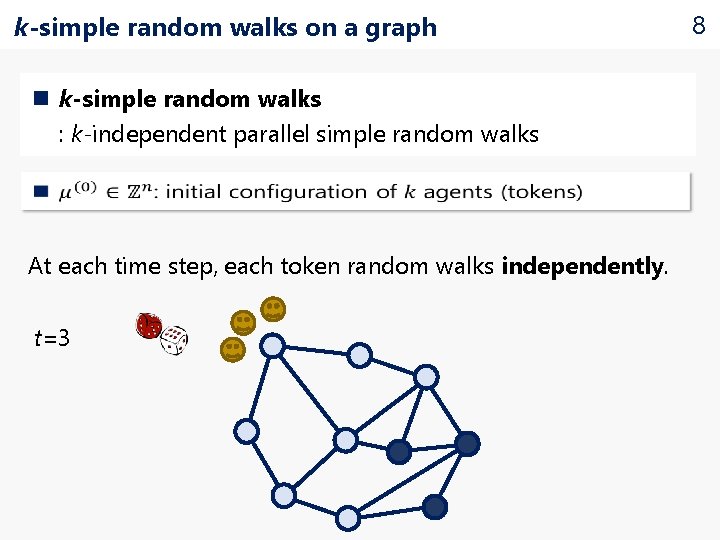
k-simple random walks on a graph n k-simple random walks : k-independent parallel simple random walks At each time step, each token random walks independently. t=3 t=2 t=1 t=0 8

9 Cover time of k-simple random walks k times speed up for small k D: diameter of G

Summary (so far) Simple RW k=1 10

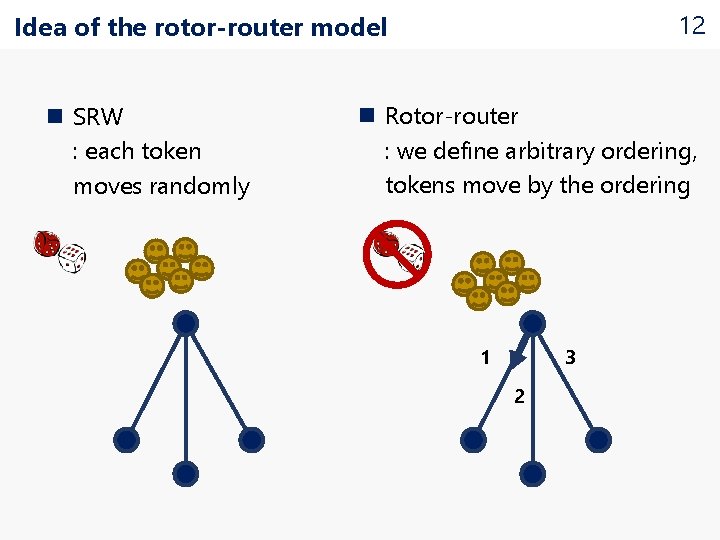
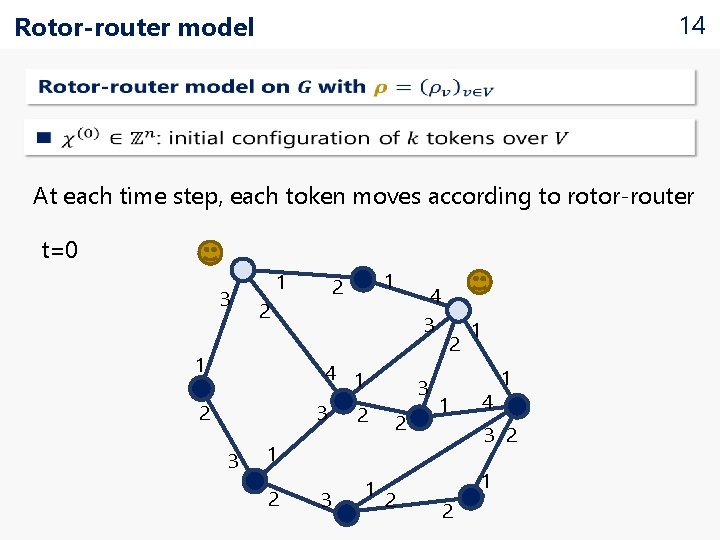
Deterministic random walk n From the view point of the deterministic graph exploration, the rotor-router model is well studied recently n Rotor-router model [Propp 2000] : deterministic analogy of a simple random walk 11

12 Idea of the rotor-router model n SRW : each token moves randomly n Rotor-router : we define arbitrary ordering, tokens move by the ordering 3 1 2

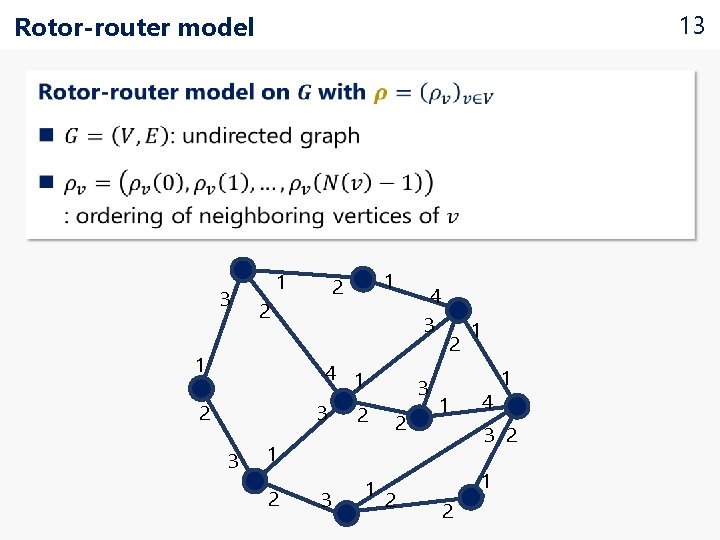
13 Rotor-router model 3 1 2 1 1 2 4 3 4 1 3 2 3 3 2 2 2 1 2 3 2 4 1 3 2 1 1 2

14 Rotor-router model At each time step, each token moves according to rotor-router t=0 3 1 2 1 1 2 4 3 4 1 3 2 3 3 2 2 2 1 2 3 2 4 1 3 2 1 1 2

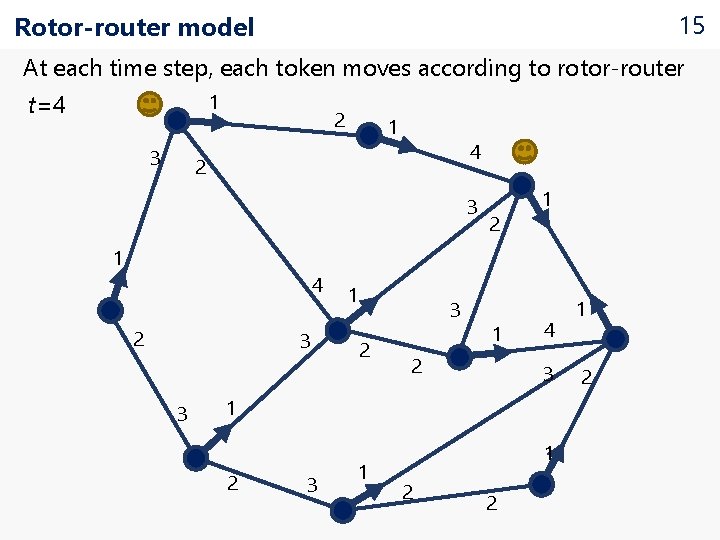
15 Rotor-router model At each time step, each token moves according to rotor-router t=4 t=3 t=2 t=1 t=0 1 3 2 1 4 2 3 2 1 1 4 2 3 3 1 3 2 1 2 4 3 1 2 3 1 1 2 2 1 2

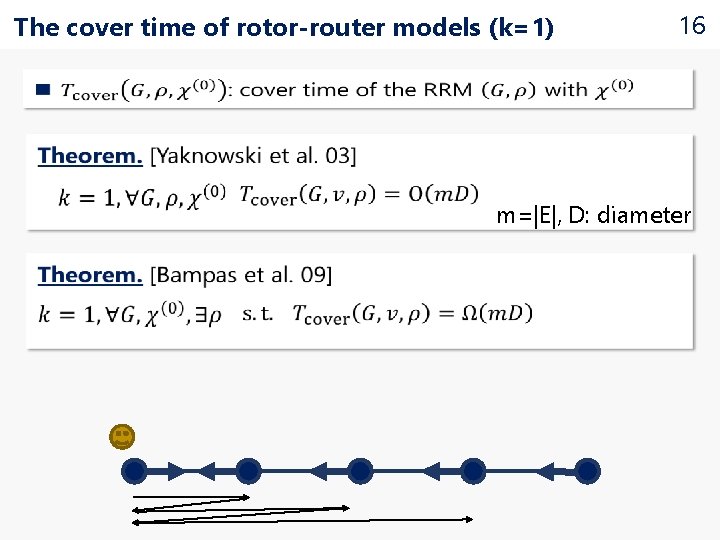
The cover time of rotor-router models (k=1) 16 m=|E|, D: diameter

17 k times speed up for small k

18 Summary (so far) Simple RW Det. simple RW (RRM) k=1

General transition probabilities

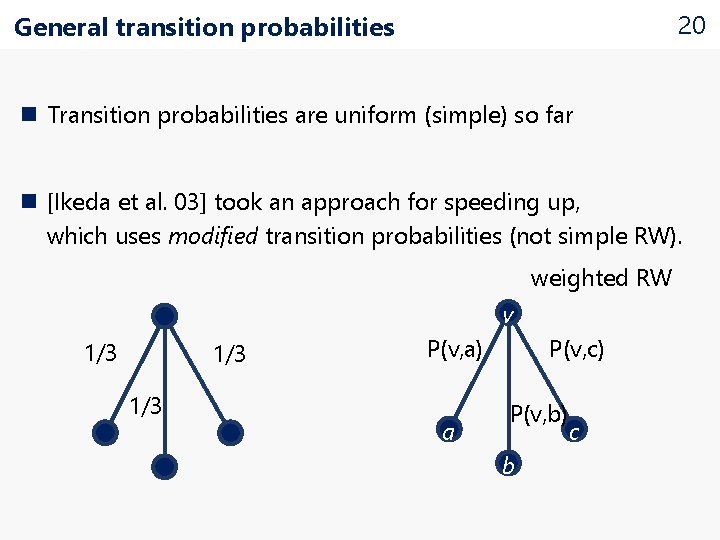
20 General transition probabilities n Transition probabilities are uniform (simple) so far n [Ikeda et al. 03] took an approach for speeding up, which uses modified transition probabilities (not simple RW). weighted RW v 1/3 1/3 P(v, c) P(v, a) a P(v, b) b c

General (not simple) random walks 1/3 1/3 21

General (not simple) random walks 22

23 Summary (so far) Simple RW Det. simple RW (RRM) k=1 Not simple RW

Det. RWs for general transition probabilities n Rotor-router model [Propp 2000] : deterministic analogy of simple random walks n Deterministic analogy of general random walks n Stack walk [Holroyd & Propp 10] n SRT-router model, Billiard router model [S. et al. 13] 24

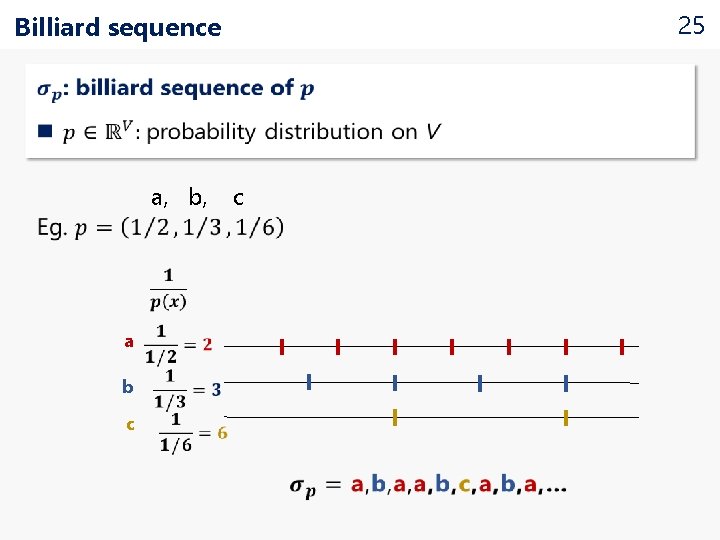
25 Billiard sequence a, b, a b c c

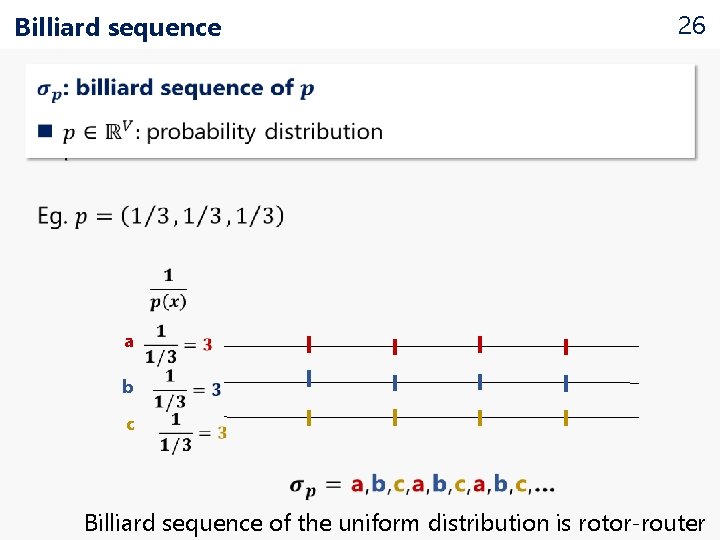
Billiard sequence 26 a b c Billiard sequence of the uniform distribution is rotor-router

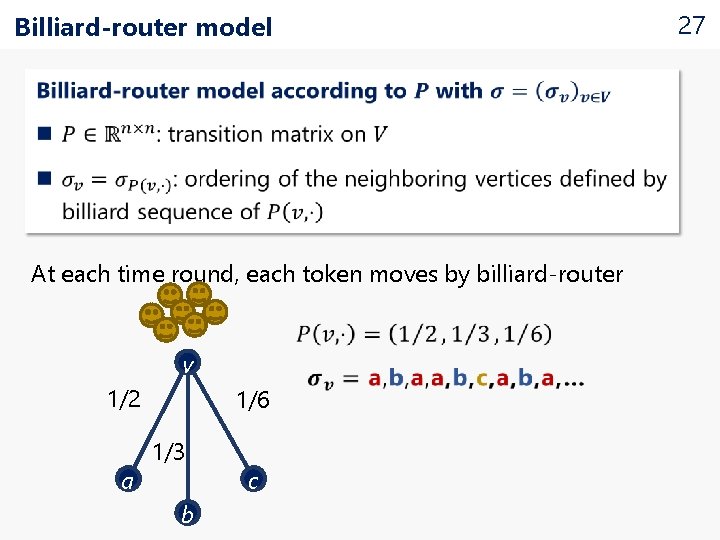
Billiard-router model At each time round, each token moves by billiard-router v 1/2 a 1/6 1/3 b c 27

Motivation and our result 28 n Nothing is known about the cover time of the deterministic random walks for general transition probabilities Results n We obtain the first result of an upper bound of the cover time for the deterministic random walks for general transition probabilities n Our upper bound improves the previous results of the rotor-router model

29 Summary (so far) Simple RW Det. simple RW (RRM) k=1 Not simple RW Not simple det. RW (BRM) ? ? ?

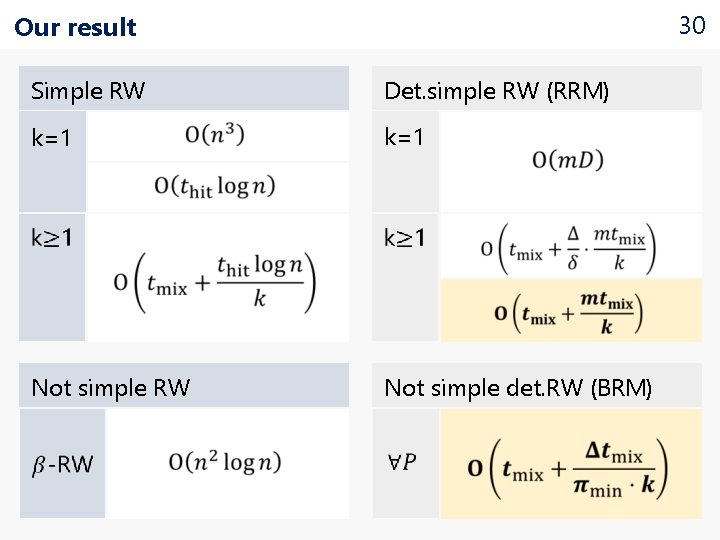
30 Our result Simple RW Det. simple RW (RRM) k=1 Not simple RW Not simple det. RW (BRM)

Main Result

32 Main result for simple RWs

Main result 33 n We obtain the first upper bound for deterministic random walks for general transition probabilities ! ※ This upper bound also holds for stack walks, SRT-router

34 Corollary for simple RWs

Upper bound for the rotor-router 35 n Our theorem improves the previous result of the rotor-router !

36 Our result Simple RW Det. simple RW (RRM) k=1 Not simple RW Not simple det. RW (BRM)

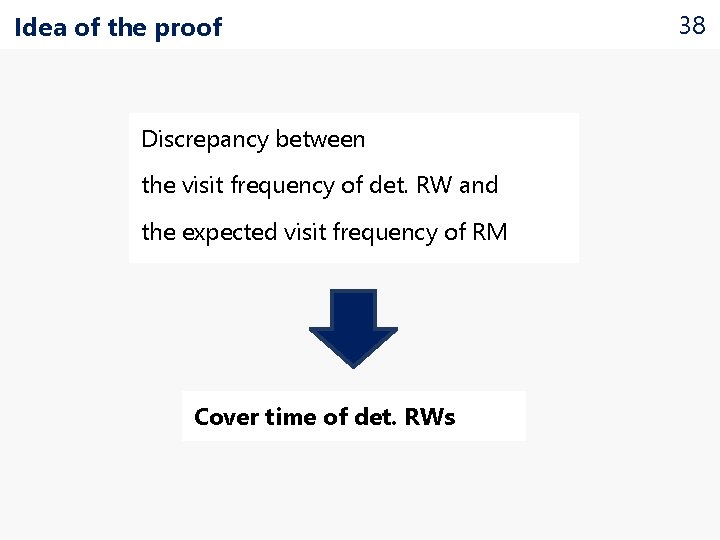
Idea of the proof

Idea of the proof Discrepancy between the visit frequency of det. RW and the expected visit frequency of RM Cover time of det. RWs 38

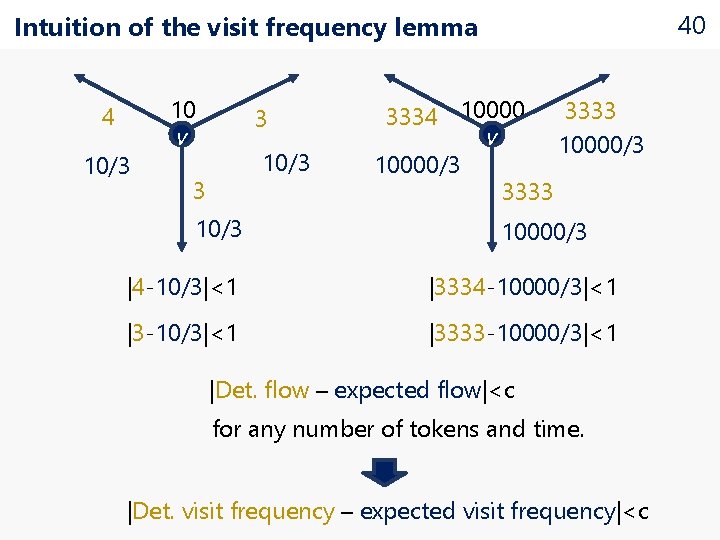
Visit frequency 39

40 Intuition of the visit frequency lemma 4 10/3 10 v 3 10/3 3333 3334 10000 v 10000/3 3333 10000/3 |4 -10/3|<1 |3334 -10000/3|<1 |3 -10/3|<1 |3333 -10000/3|<1 |Det. flow – expected flow|<c for any number of tokens and time. |Det. visit frequency – expected visit frequency|<c

Visit frequency and the cover time 41

Visit frequency and the cover time 42

Visit frequency and the cover time 43 n w has been visited ! n We obtain the upper bound of the cover time if the discrepancy between visit frequencies is upper bounded.

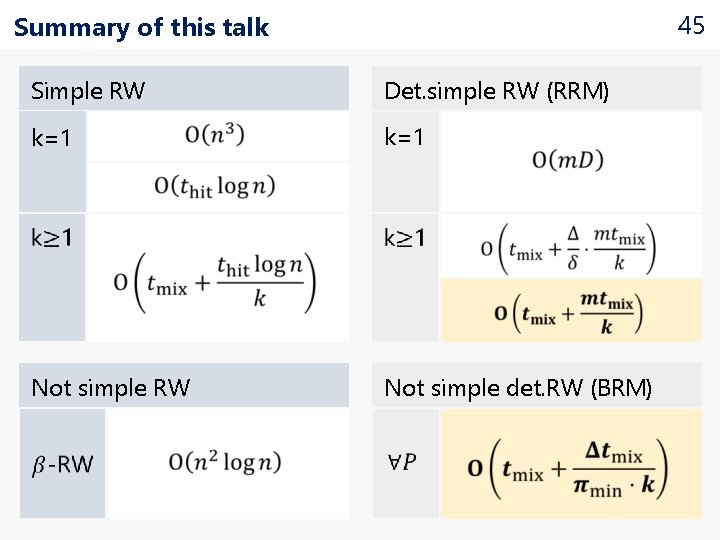
Conclusion

45 Summary of this talk Simple RW Det. simple RW (RRM) k=1 Not simple RW Not simple det. RW (BRM)

Future works 46

Thank you for the attention ! The Cover Time of Deterministic Random Walks for General Transition Probabilities Takeharu Shiraga* *Kyushu University, Japan

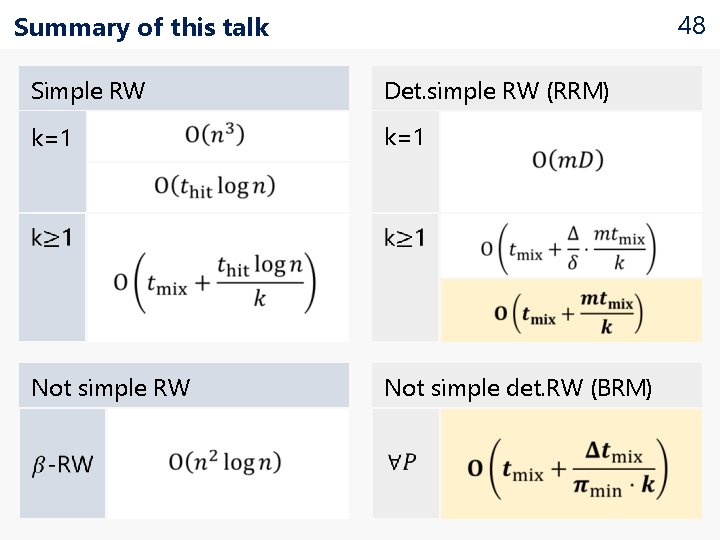
48 Summary of this talk Simple RW Det. simple RW (RRM) k=1 Not simple RW Not simple det. RW (BRM)

memo

Hitting time and cover time 50

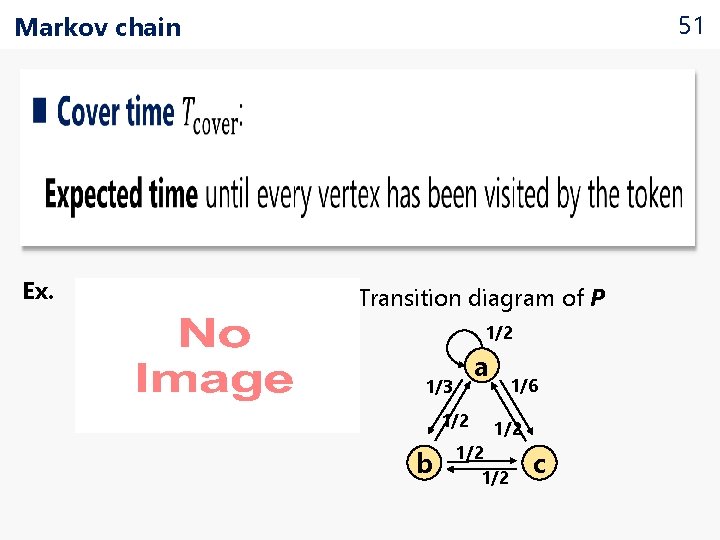
51 Markov chain • Ex. Transition diagram of P 1/2 a 1/3 1/2 b 1/6 1/2 1/2 c

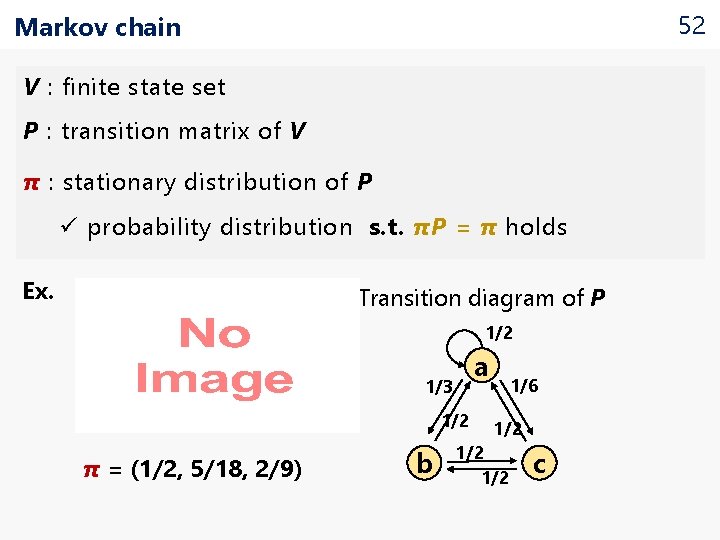
52 Markov chain V : finite state set P : transition matrix of V π : stationary distribution of P ü probability distribution s. t. πP = π holds Ex. Transition diagram of P 1/2 a 1/3 1/2 π = (1/2, 5/18, 2/9) b 1/6 1/2 1/2 c

Limit theorem The following theorem is fundamental ※It is often assumed that P is ergodic, defined as follows. 53

54 Mixing time Let’s introduce a characterization of ``convergence speed’’ ü Thus, after t steps s. t. t>τ(ε), we can get samples according to approximate π within ratio ε ! ( in the sense that total variation distance ) (L 1 -disc. )

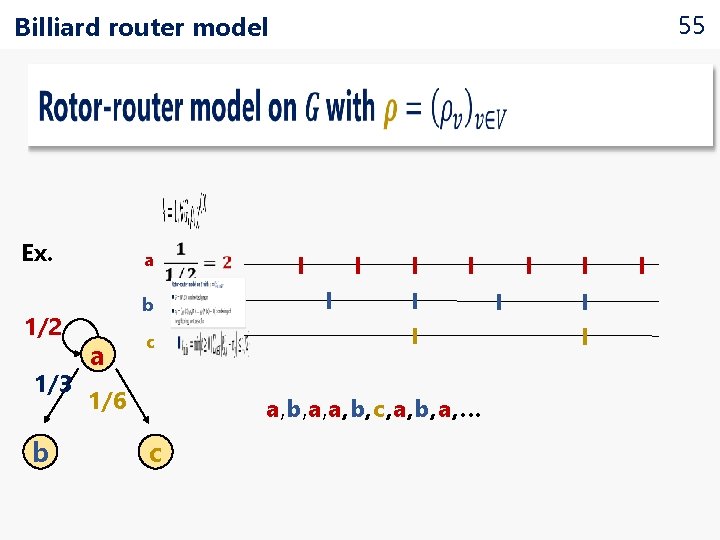
Billiard router model • Ex. 1/2 1/3 b a c 1/6 a, b, a, a, b, c, a, b, a, … c 55

The discrepancy of sequences 56

SRT router [Tijdeman 80, Angel et al. 10] • Ex. 1/2 1/3 b a c 1/6 a, b, … c 57

The discrepancy of sequences 58