Intro to Deterministic Analysis leftcontinuous Deterministic network calculus

Intro to Deterministic Analysis left-continuous

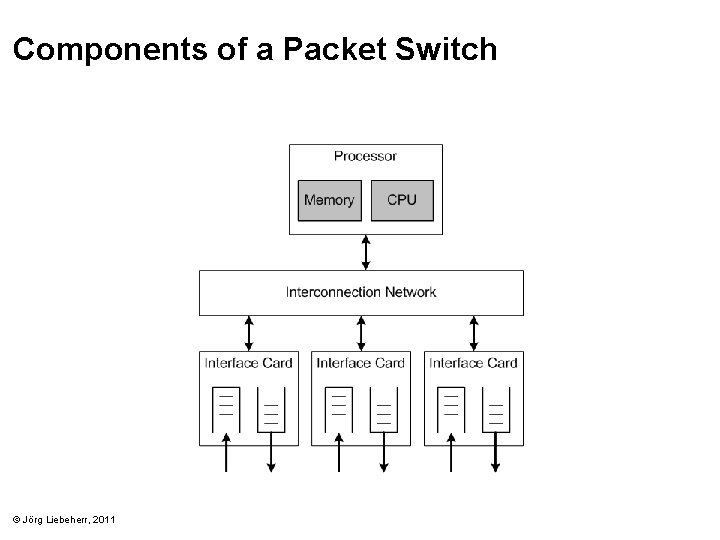
• Deterministic network calculus: – Theory for obtain worst-case (=deterministic) network performance – Developed in the 1990 s (Rene Cruz) – Bounds of interest: • Delay at a switch • Backlog at a switch • Traffic at output of switch © Jörg Liebeherr, 2011

Components of a Packet Switch © Jörg Liebeherr, 2011

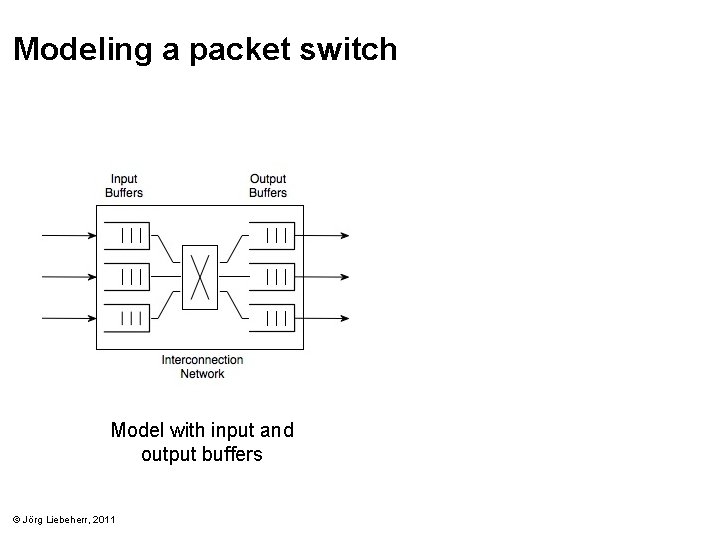
Modeling a packet switch Model with input and output buffers © Jörg Liebeherr, 2011

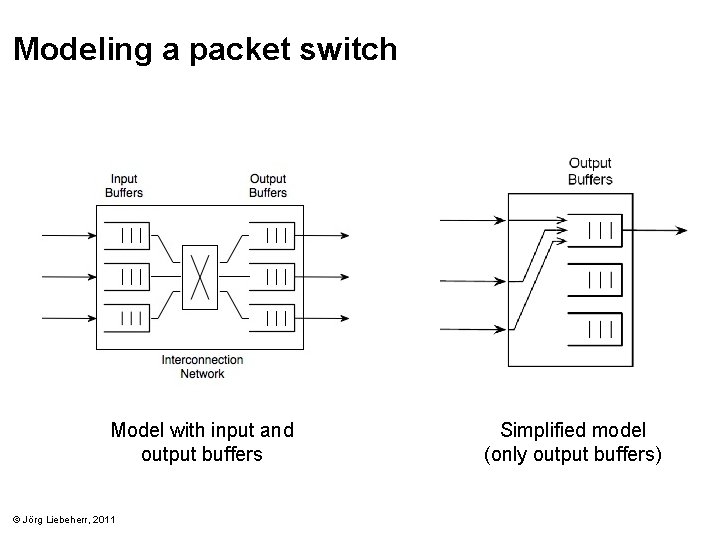
Modeling a packet switch Model with input and output buffers © Jörg Liebeherr, 2011 Simplified model (only output buffers)

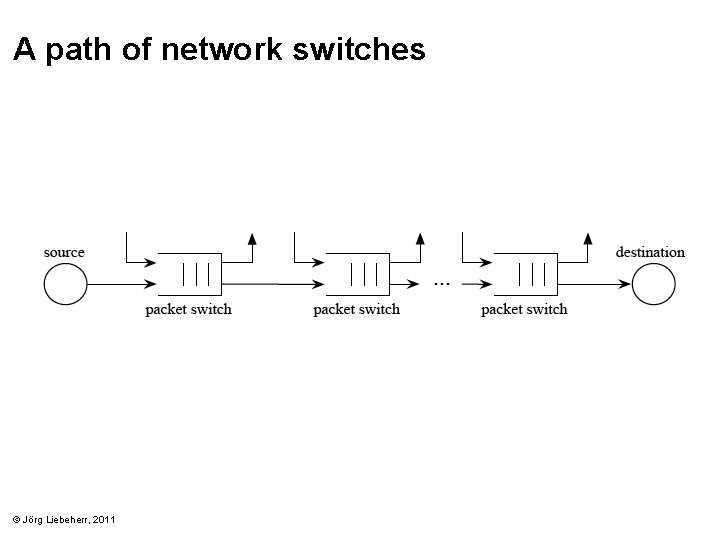
A path of network switches © Jörg Liebeherr, 2011

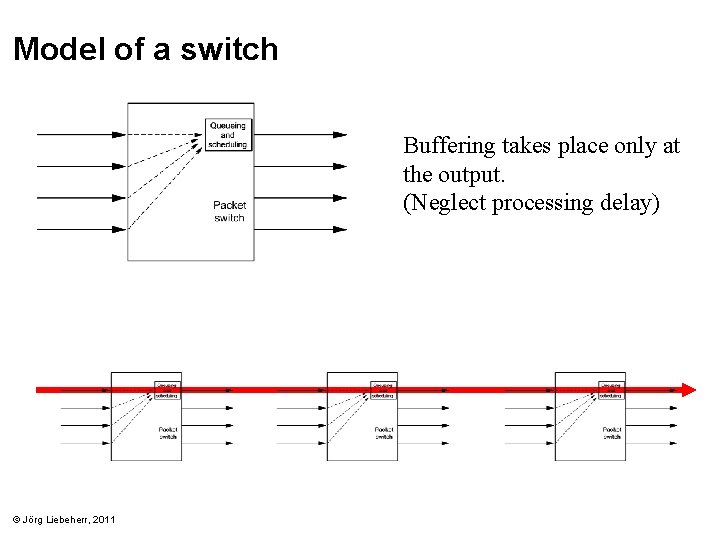
Model of a switch Buffering takes place only at the output. (Neglect processing delay) © Jörg Liebeherr, 2011

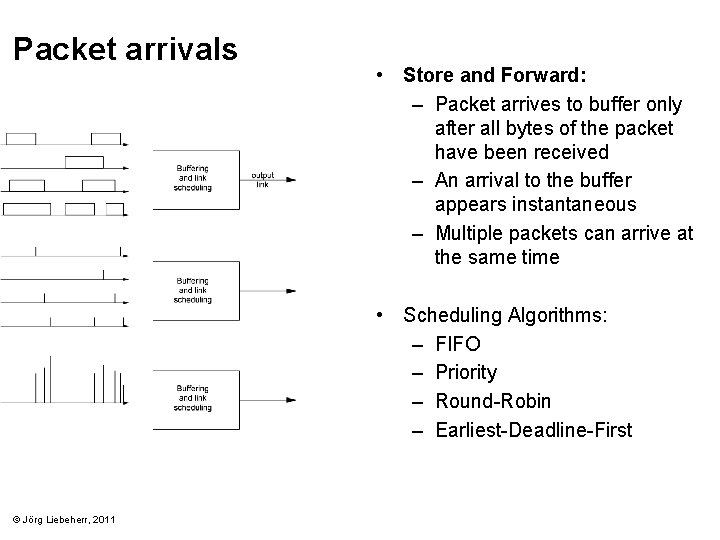
Packet arrivals • Store and Forward: – Packet arrives to buffer only after all bytes of the packet have been received – An arrival to the buffer appears instantaneous – Multiple packets can arrive at the same time • Scheduling Algorithms: – FIFO – Priority – Round-Robin – Earliest-Deadline-First © Jörg Liebeherr, 2011

Modeling Traffic Arrivals • We write arrivals as functions of time: A(t) : Arrivals until time t, measured in bits • There a number of choices to be made: 1. Continuous time or Discrete time domain 2. Discrete sized or fluid flow traffic 3. Left-continuous or right-continuous © Jörg Liebeherr, 2011

Continuous time vs. Discrete time Domain • Continous time: t is a non-negative real number • Discrete time: Time is divided in clock ticks t = 0, 1, 2, …. © Jörg Liebeherr, 2011

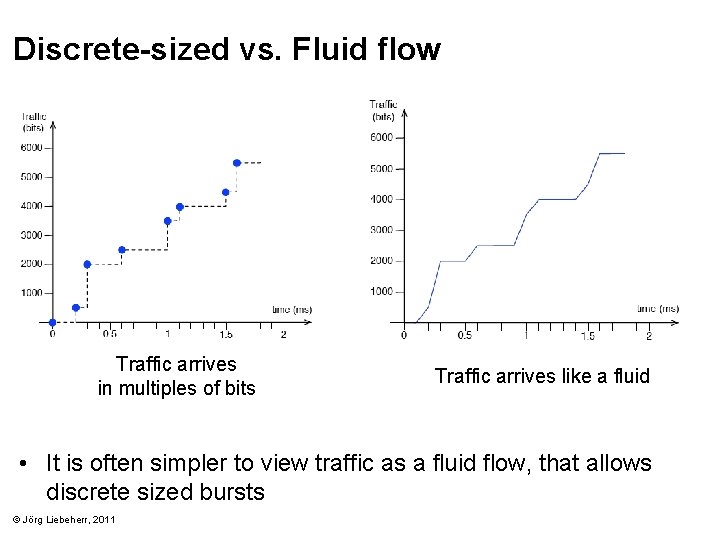
Discrete-sized vs. Fluid flow Traffic arrives in multiples of bits Traffic arrives like a fluid • It is often simpler to view traffic as a fluid flow, that allows discrete sized bursts © Jörg Liebeherr, 2011

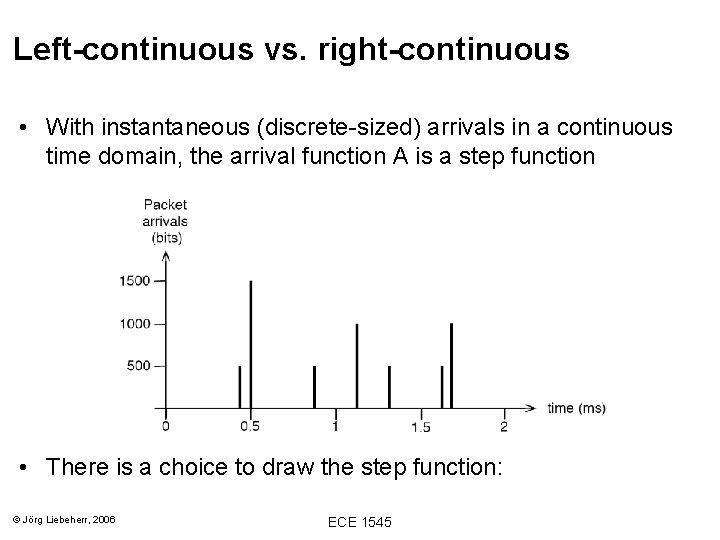
Left-continuous vs. right-continuous • With instantaneous (discrete-sized) arrivals in a continuous time domain, the arrival function A is a step function • There is a choice to draw the step function: © Jörg Liebeherr, 2006 ECE 1545

Left-continuous vs. right-continuous A(t) considers arrivals in (0, t] left-continuous A(t) considers arrivals in [0, t) (Note: A(0) = 0 !) • We will use a left-continuous arrival function © Jörg Liebeherr, 2011

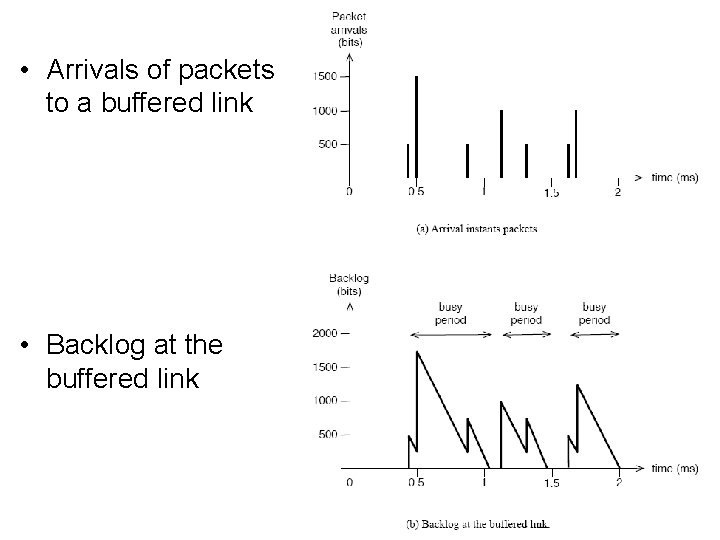
• Arrivals of packets to a buffered link • Backlog at the buffered link

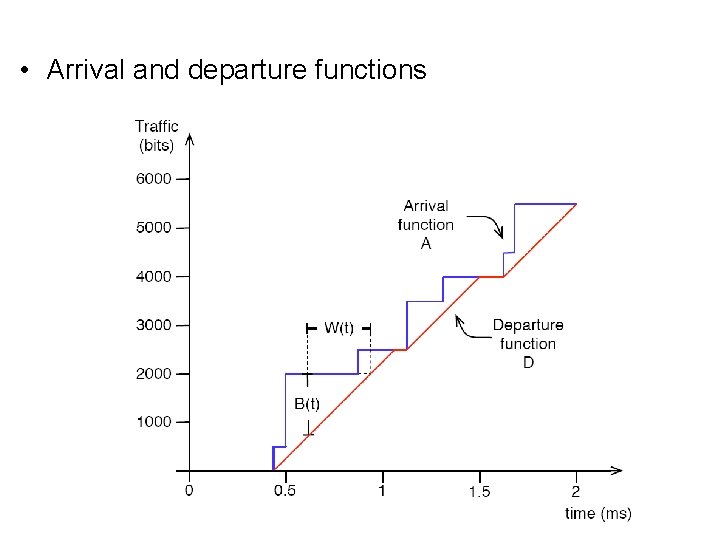
• Arrival and departure functions

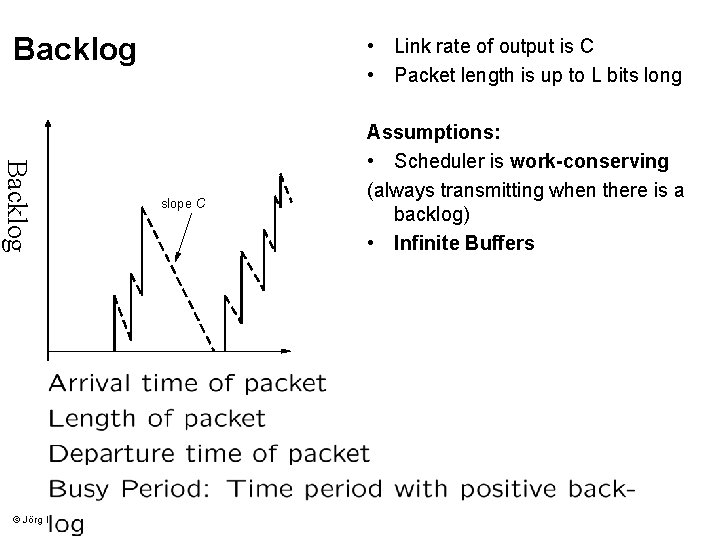
Backlog © Jörg Liebeherr, 2006 • Link rate of output is C • Packet length is up to L bits long slope C Assumptions: • Scheduler is work-conserving (always transmitting when there is a backlog) • Infinite Buffers ECE 1545

Definitions: © Jörg Liebeherr, 2006 ECE 1545

Dealing with instantaneous arrivals • If we have an instantaneous arrival, then the arrival function is a step function. • Need to decide which time the arrival takes place. • We assume that the arrival occurs at time t+ • This leads to a left-continuous arrival function. © Jörg Liebeherr, 2006 ECE 1545

© Jörg Liebeherr, 2006 ECE 1545