SVVRL IM NTU Sorting Algorithms and Their Efficiency

SVVRL @ IM. NTU Sorting Algorithms and Their Efficiency Yih-Kuen Tsay Dept. of Information Management National Taiwan University Based on [Carrano and Henry 2013] With help from Chien Chin Chen 1 / 52

Sorting Algorithms n Sorting: q q A process that organizes a collection of data into either ascending or descending order. The sort key n n SVVRL @ IM. NTU The part of a data item that we consider when sorting a data collection. Categories of sorting algorithms. q An internal sort: n q Requires that the collection of data fit entirely in the computer’s main memory. An external sort: n Yih-Kuen Tsay The collection of data will not fit in the computer’s main memory all at once, but must reside in secondary storage. DS 2015: Sorting Algorithms and Their Efficiency 2 / 52

Determining Efficiency n Sorting in general compares, exchanges, or moves items. q q n n SVVRL @ IM. NTU We should count these operations. Such operations are more expensive than ones that control loops or manipulate array indexes, particularly when the data to be sorted are complex. A sorting algorithm typically proceeds in stages/iterations. To determine its execution time, we calculate q q The number of iterations The number of steps/operations in each iteration Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 3 / 52

Selection Sort (1/8) SVVRL @ IM. NTU Source: FIGURE 11 -1 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 4 / 52

Selection Sort (2/8) SVVRL @ IM. NTU /** Finds the largest item in an array. @pre The size of the array is >= 1. @post The arguments are unchanged. @param the. Array The given array. @param size The number of elements in the. Array. @return The index of the largest entry in the array. */ int find. Indexof. Largest(const Item. Type the. Array[], int size); /** Sorts the items in an array into ascending order. @pre None. @post The array is sorted into ascending order; the size of the array is unchanged. @param the. Array The array to sort. @param n The size of the. Array. */ void selection. Sort(Item. Type the. Array[], int n) Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 5 / 52

Selection Sort (3/8) SVVRL @ IM. NTU void selection. Sort(Item. Type the. Array[], int n) { // last = index of the last item in the subarray of items yet // to be sorted; // largest = index of the largest item found for (int last = n - 1; last >= 1; last--) { // At this point, the. Array[last+1. . n-1] is sorted, and its // entries are greater than those in the. Array[0. . last]. // Select the largest entry in the. Array[0. . last] int largest = find. Indexof. Largest(the. Array, last + 1); // Swap the largest entry, the. Array[largest], with // the. Array[last] std: : swap(the. Array[largest], the. Array[last]); } // end for } // end selection. Sort Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 6 / 52

Selection Sort (4/8) SVVRL @ IM. NTU int find. Indexof. Largest(const Item. Type the. Array[], int size) { int index. So. Far = 0; // Index of largest entry found so far for (int current. Index = 1; current. Index < size; current. Index++) { // At this point, the. Array[index. So. Far] >= all entries in // the. Array[0. . current. Index - 1] if (the. Array[current. Index] > the. Array[index. So. Far]) index. So. Far = current. Index; } // end for return index. So. Far; // Index of largest entry } // end find. Indexof. Largest Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 7 / 52

Selection Sort (5/8) n Again, q q n SVVRL @ IM. NTU Sorting in general compares, exchanges, or moves items. Such operations are the more expensive ones. The for loop in the function selection. Sort executes n-1 times. q find. Index. Of. Largest and swap are called n-1 times. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 8 / 52

SVVRL @ IM. NTU Selection Sort (6/8) n Each call to find. Index. Of. Largest causes its loop to execute last (or size – 1) times. q The loop executes a total of: n q (n-1) + (n-2) + … + 1 = n×(n-1)/2 times. Each execution of the loop performs one comparison: n Yih-Kuen Tsay The calls of find. Index. Of. Largest require n×((n-1)/2 comparisons. DS 2015: Sorting Algorithms and Their Efficiency 9 / 52

Selection Sort (7/8) n The n-1 calls to swap require: q n 3×(n-1) moves. Together, a Selection sort of n items requires: q n SVVRL @ IM. NTU n×(n-1)/2 + 3(n-1) = n 2/2 + 5 n/2 -3 major operations. Thus, Selection sort is O(n 2). Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 10 / 52

Selection Sort (8/8) n SVVRL @ IM. NTU Does not depend on the initial arrangement of the data. q q Best case = worst case = average case = O(n 2) Only appropriate for small n!! Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 11 / 52

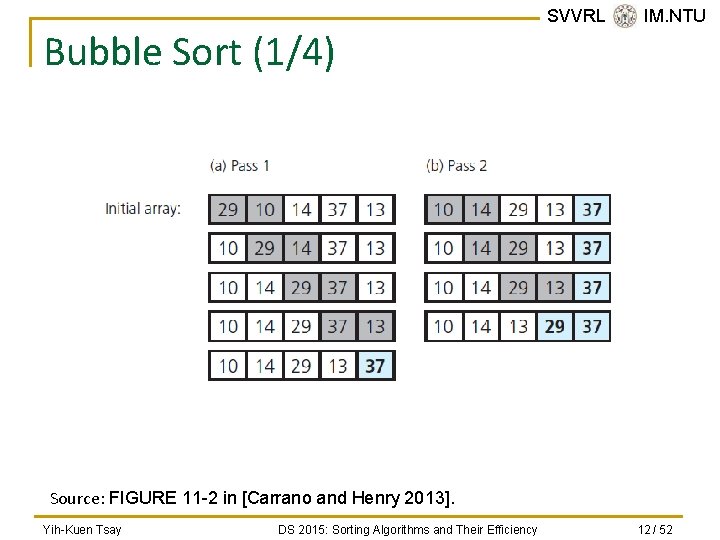
Bubble Sort (1/4) SVVRL @ IM. NTU Source: FIGURE 11 -2 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 12 / 52

Bubble Sort (2/4) SVVRL @ IM. NTU /** Sorts the items in an array into ascending order. @pre None. @post the. Array is sorted into ascending order; n is unchanged. @param the. Array The given array. @param n The size of the. Array. */ void bubble. Sort(Item. Type the. Array[], int n) { bool sorted = false; // False when swaps occur int pass = 1; while (!sorted && (pass < n)) { // At this point, the. Array[n+1 -pass. . n-1] is sorted // and all of its entries are > the entries in // the. Array[0. . n-pass] Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 13 / 52

Bubble Sort (3/4) SVVRL @ IM. NTU while (!sorted && (pass < n)) { // At this point, the. Array[n+1 -pass. . n-1] is sorted // and all of its entries are > the entries in // the. Array[0. . n-pass] sorted = true; // Assume sorted for (int index = 0; index < n - pass; index++) { // At this point, all entries in the. Array[0. . index-1] // are <= the. Array[index] int next. Index = index + 1; if (the. Array[index] > the. Array[next. Index]) { // Exchange entries std: : swap(the. Array[index], the. Array[next. Index]); sorted = false; // Signal exchange } // end if } // end for // Assertion: the. Array[0. . n-pass-1] < the. Array[n-pass] pass++; } // end while Yih-Kuen } // end. Tsay bubble. Sort DS 2015: Sorting Algorithms and Their Efficiency 14 / 52

Bubble Sort (4/4) n SVVRL @ IM. NTU Analysis: q In the worst case, the bubble sort requires at most n-1 passes through the array. n n n q Pass 1 requires n-1 comparisons and at most n-1 exchanges. Pass 2 require n-2 comparisons and at most n-2 exchanges. . Require a total of q (n-1) + (n-2) + … + 1 = n*(n-1)/2 comparisons. q (n-1) + (n-2) + … + 1 = n*(n-1)/2 exchanges. § Each exchange require 3 moves. Thus, altogethere are: 2 * n*(n-1) = O(n 2) In the best case: require only one pass. n Yih-Kuen Tsay n-1 comparisons and no exchanges: O(n) DS 2015: Sorting Algorithms and Their Efficiency 15 / 52

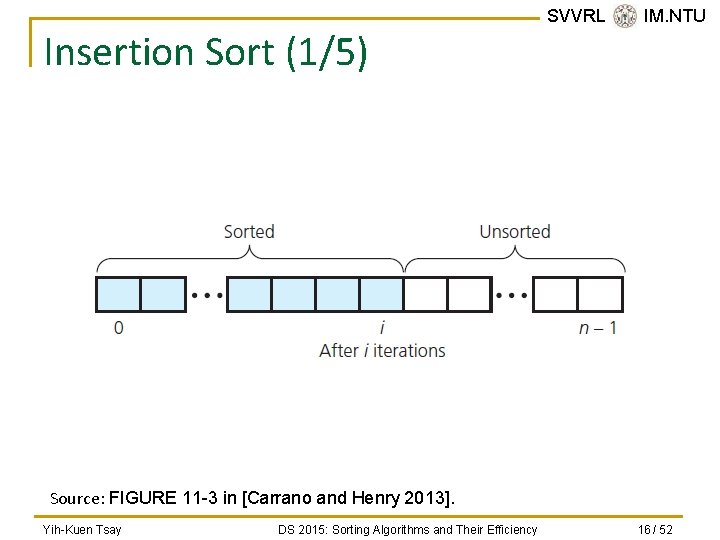
Insertion Sort (1/5) SVVRL @ IM. NTU Source: FIGURE 11 -3 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 16 / 52

Insertion Sort (2/5) SVVRL @ IM. NTU Source: FIGURE 11 -4 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 17 / 52

Insertion Sort (3/5) SVVRL @ IM. NTU /** Sorts the items in an array into ascending order. @pre None. @post the. Array is sorted into ascending order; n is unchanged. @param the. Array The given array. @param n The size of the. Array. */ void insertion. Sort(Item. Type the. Array[], int n) { // unsorted = first index of the unsorted region, // loc = index of insertion in the sorted region, // next. Item = next item in the unsorted region. // Initially, sorted region is the. Array[0], // unsorted region is the. Array[1. . n-1]. // In general, sorted region is the. Array[0. . unsorted-1], // unsorted region the. Array[unsorted. . n-1] for (int unsorted = 1; unsorted < n; unsorted++) { Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 18 / 52

Insertion Sort (4/5) SVVRL @ IM. NTU for (int unsorted = 1; unsorted < n; unsorted++) { // At this point, the. Array[0. . unsorted-1] is sorted. // Find the right position (loc) in the. Array[0. . unsorted] // for the. Array[unsorted], which is the first entry in the // unsorted region; shift, if necessary, to make room Item. Type next. Item = the. Array[unsorted]; int loc = unsorted; while ((loc > 0) && (the. Array[loc - 1] > next. Item)) { // Shift the. Array[loc - 1] to the right the. Array[loc] = the. Array[loc - 1]; loc--; } // end while // At this point, the. Array[loc] is where next. Item belongs // Insert next. Item into sorted region the. Array[loc] = next. Item; } // end for } // end insertion. Sort Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 19 / 52

Insertion Sort (5/5) n SVVRL @ IM. NTU Analysis: q q In the worst case, the outer for loop executes n-1 times. This loop contains an inner for loop that executes at most unsorted times. n n q q unsorted ranges from 1 to n-1. Number of comparisons and moves: q 2 ×[1+2+…+(n-1)] = n×(n-1). The outer loop moves data items twice per iteration, or 2×(n-1) times. Together, there are n*(n-1) + 2×(n-1) = n 2+n-2 major operations in the worst case, O(n 2). n Yih-Kuen Tsay Prohibitively inefficient for large arrays. DS 2015: Sorting Algorithms and Their Efficiency 20 / 52

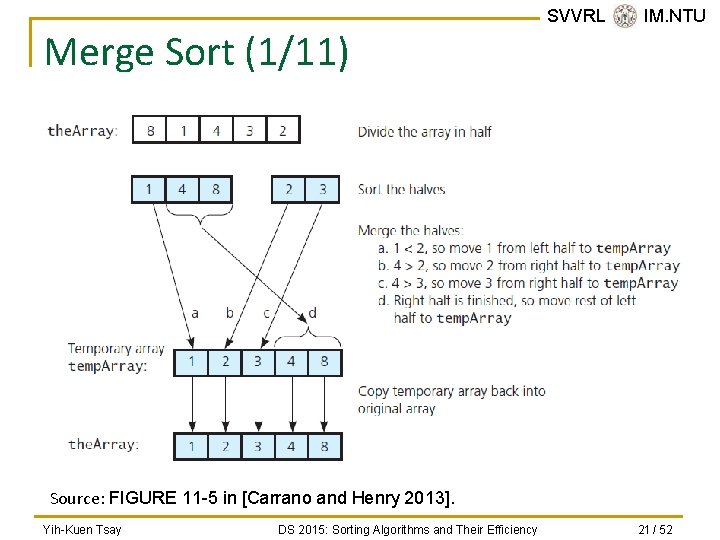
Merge Sort (1/11) SVVRL @ IM. NTU Source: FIGURE 11 -5 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 21 / 52

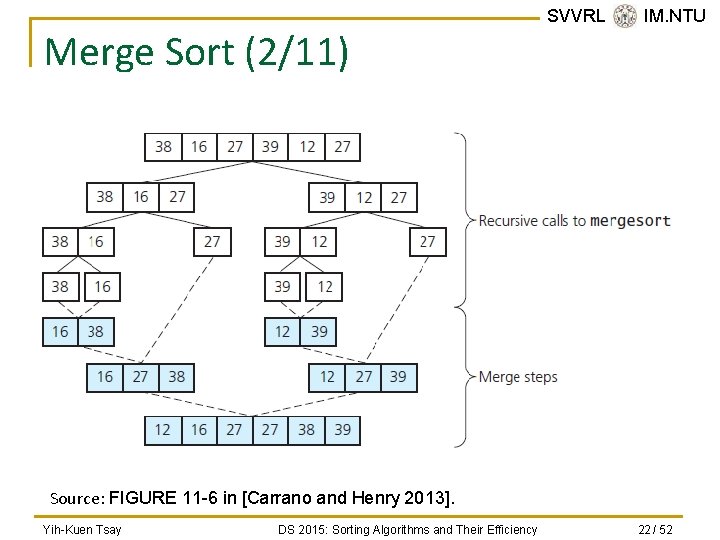
Merge Sort (2/11) SVVRL @ IM. NTU Source: FIGURE 11 -6 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 22 / 52

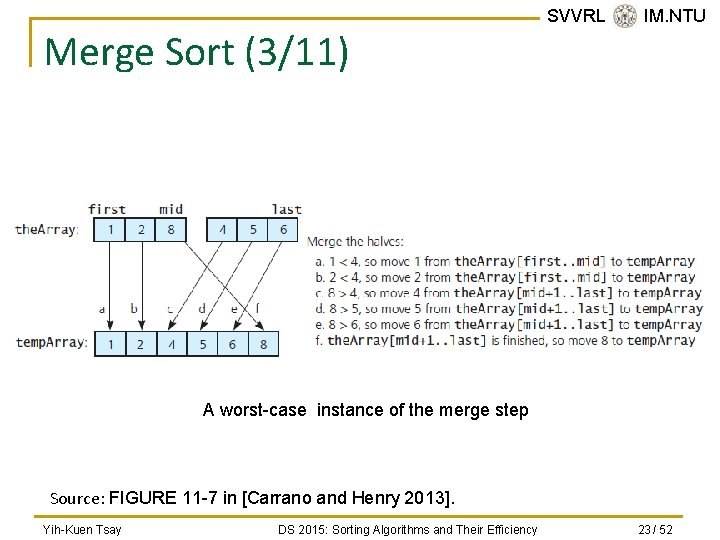
Merge Sort (3/11) SVVRL @ IM. NTU A worst-case instance of the merge step Source: FIGURE 11 -7 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 23 / 52

Merge Sort (4/11) SVVRL @ IM. NTU const int MAX_SIZE = maximum-number-of-items-in-array; /** Merges two sorted array segments the. Array[first. . mid] and the. Array[mid+1. . last] into one sorted array. @pre first <= mid <= last. The subarrays the. Array[first. . mid] and the. Array[mid+1. . last] are each sorted in increasing order. @post the. Array[first. . last] is sorted. @param the. Array The given array. @param first The index of the beginning of the first segment in the. Array. @param mid The index of the end of the first segment in the. Array; mid + 1 marks the beginning of the second segment. @param last The index of the last element in the second segment in the. Array. @note This function merges the two subarrays into a temporary array and copies the result into the original array the. Array. */ void merge(Item. Type the. Array[], int first, int mid, int last) Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 24 / 52

Merge Sort (5/11) SVVRL @ IM. NTU void merge(Item. Type the. Array[], int first, int mid, int last) { Item. Type temp. Array[MAX_SIZE]; // Temporary array // Initialize the local indices to indicate the subarrays int first 1 = first; // Beginning of first subarray int last 1 = mid; // End of first subarray int first 2 = mid + 1; // Beginning of second subarray int last 2 = last; // End of second subarray // While both subarrays are not empty, copy the // smaller item into the temporary array int index = first 1; // Next available location in temp. Array while ((first 1 <= last 1) && (first 2 <= last 2)) // At this point, temp. Array[first. . index-1] is in order if (the. Array[first 1] <= the. Array[first 2]) temp. Array[index++] = the. Array[first 1++]; else temp. Array[index++] = the. Array[first 2++]; Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 25 / 52

Merge Sort (6/11) SVVRL @ IM. NTU // Finish off the first subarray, if necessary while (first 1 <= last 1) // At this point, temp. Array[first. . index-1] is in order temp. Array[index++] = the. Array[first 1++]; // Finish off the second subarray, if necessary while (first 2 <= last 2) // At this point, temp. Array[first. . index-1] is in order temp. Array[index++] = the. Array[first 2++]; // Copy the result back into the original array for (index = first; index <= last; index++) the. Array[index] = temp. Array[index]; } // end merge Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 26 / 52

Merge Sort (7/11) SVVRL @ IM. NTU /** Sorts the items in an array into ascending order. @pre the. Array[first. . last] is an array. @post the. Array is sorted into ascending order. @param the. Array The given array. @param first The index of the first entry to consider. @param last The index of the last entry to consider. */ void merge. Sort(Item. Type the. Array[], int first, int last) { if (first < last) { // Sort each half int mid = first + (last – first) / 2; // Index of midpoint // Sort left half the. Array[first. . mid] merge. Sort(the. Array, first, mid); // Sort right half the. Array[mid+1. . last] merge. Sort(the. Array, mid + 1, last); // Merge the two halves merge(the. Array, first, mid, last); } // end if } // end merge. Sort Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 27 / 52

Mergesort (8/11) n SVVRL @ IM. NTU Analysis (worst case): q The merge step of the algorithm requires the most effort. n n Each merge step merges the. Array[first…mid] and the. Array[mid+1…last]. If the number of items in the two array segment is m: q Merging the segments requires at most: § § § q Yih-Kuen Tsay m-1 comparisons. m moves from the original array to the temporary array. m moves from the temporary array back to the original array. Each merge requires 3×m-1 major operations. DS 2015: Sorting Algorithms and Their Efficiency 28 / 52

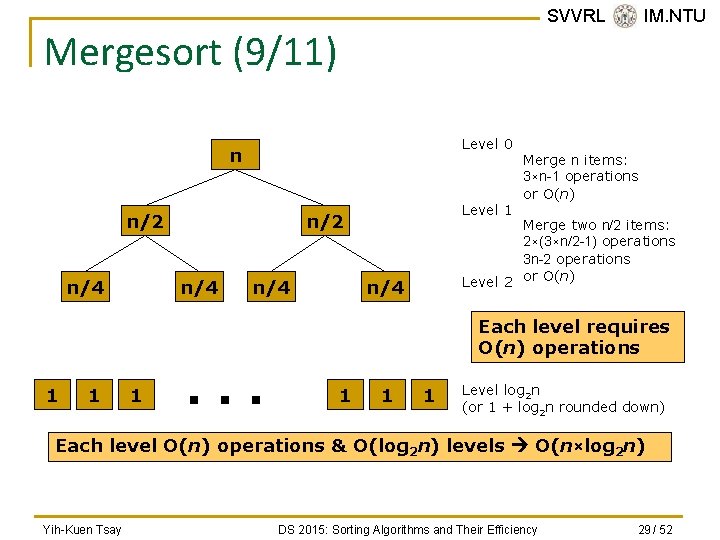
SVVRL @ IM. NTU Mergesort (9/11) Level 0 n n/2 n/4 Level 1 n/2 n/4 Merge n items: 3×n-1 operations or O(n) Merge two n/2 items: 2×(3×n/2 -1) operations 3 n-2 operations Level 2 or O(n) n/4 Each level requires O(n) operations 1 1 1 . . . 1 1 1 Level log 2 n (or 1 + log 2 n rounded down) Each level O(n) operations & O(log 2 n) levels O(n×log 2 n) Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 29 / 52

Mergesort (10/11) n SVVRL @ IM. NTU Analysis: q q Worst case: O(n × log 2 n). Average case: O(n × log 2 n). Performance is independent of the initial order of the array items. Advantage: n q Mergesort is an extremely fast algorithm. Disadvantage: n Yih-Kuen Tsay Mergesort requires a second array as large as the original array. DS 2015: Sorting Algorithms and Their Efficiency 30 / 52

Merge Sort (11/11) n SVVRL @ IM. NTU A variant of the last three loops of merging: if (first 2 > last 2) { // Finish off the first subarray while (first 1 <= last 1) // At this point, temp. Array[first. . index-1] is in order temp. Array[index++] = the. Array[first 1++]; else // Need not finish off the second subarray, as the // items are already in their eventual correct places. // Remember not to copy “them” back from temp. Array last = first 2 - 1; // Copy the result back into the original array for (index = first; index <= last; index++) the. Array[index] = temp. Array[index]; } // end merge Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 31 / 52

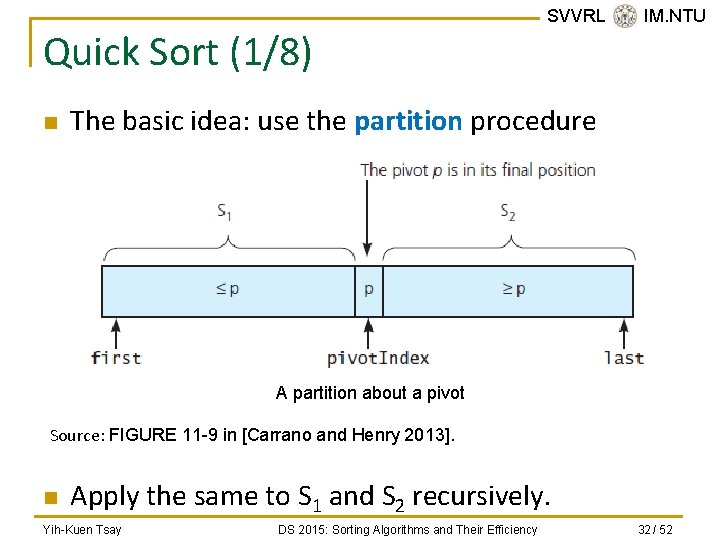
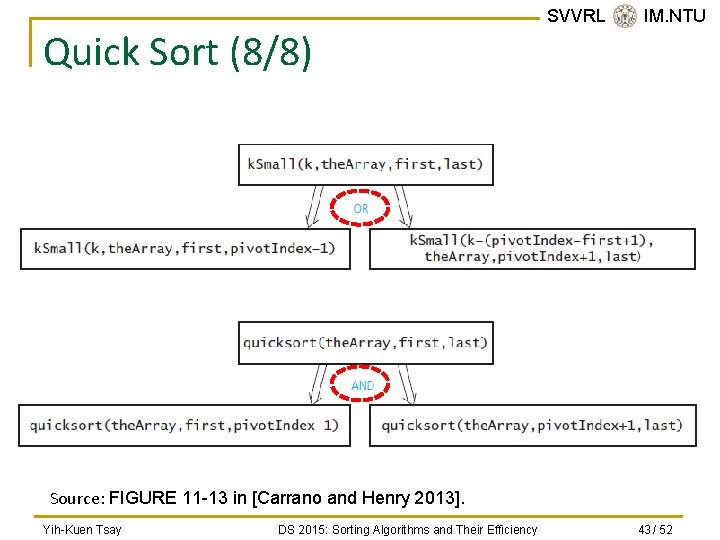
Quick Sort (1/8) n SVVRL @ IM. NTU The basic idea: use the partition procedure A partition about a pivot Source: FIGURE 11 -9 in [Carrano and Henry 2013]. n Apply the same to S 1 and S 2 recursively. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 32 / 52

SVVRL @ IM. NTU Quick Sort (2/8) n Draft of the algorithm in pseudocode: // Sorts the. Array[first. . last]. quick. Sort(the. Array: Item. Array, first: integer, last: integer): void if (first < last) { Choose a pivot item p from the. Array[first. . last] Partition the items of the. Array[first. . last] about p // The partition is the. Array[first. . pivot. Index. . last], // which may be depicted as S 1 | p | S 2 quick. Sort(the. Array, first, pivot. Index - 1) // Sort S 1 quick. Sort(the. Array, pivot. Index + 1, last) // Sort S 2 } // If first >= last, there is nothing to do Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 33 / 52

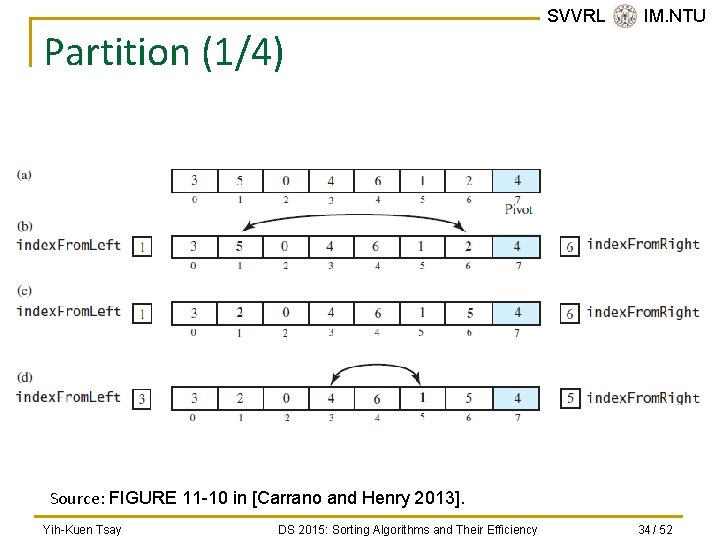
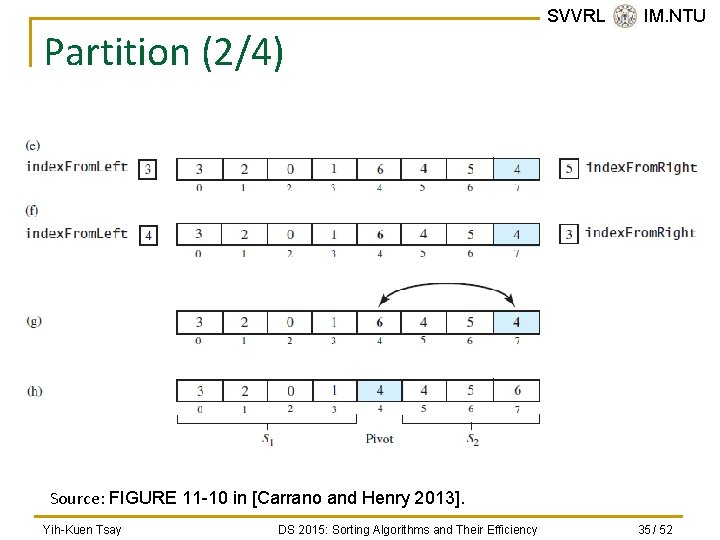
Partition (1/4) SVVRL @ IM. NTU Source: FIGURE 11 -10 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 34 / 52

Partition (2/4) SVVRL @ IM. NTU Source: FIGURE 11 -10 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 35 / 52

Partition (3/4) SVVRL @ IM. NTU // Partition with simple pivot selection partition(the. Array: Item. Array, first: integer, last: integer): integer // Choose last entry as pivot // May also choose another and exchange it with last entry pivot. Index = last pivot = the. Array[pivot. Index] // Determine the regions S 1 and S 2 index. From. Left = first index. From. Right = last – 1 done = false while (not done) { // Locate first entry on left that is ≥ pivot while (thearray[index. From. Left] < pivot) index. From. Left = index. From. Left + 1 // Locate first entry on right that is ≤ pivot while (thearray[index. From. Right] > pivot) index. From. Right = index. From. Right – 1 Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 36 / 52

Partition (4/4) SVVRL @ IM. NTU if (index. From. Left < index. From. Fight) { Interchange the. Array[index. From. Left] and the. Array[index. From. Fight] index. From. Left = index. From. Left + 1 index. From. Right = index. From. Right – 1 } else done = true } // Place pivot in proper position between S 1 and S 2, and // mark its new location Interchange the. Array[pivot. Index] and the. Array[index. From. Left] pivot. INdex = index. From. Left return pivot. Index Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 37 / 52

Quick Sort (3/8) SVVRL @ IM. NTU /** Sorts an array into ascending order. Uses the quick sort with median-of-three pivot selection for arrays of at least MIN_SIZE entries, and uses the insertion sort for other arrays. @pre the. Array[first. . last] is an array. @post the. Array[first. . last] is sorted. @param the. Array The given array. @param first The first element to consider in the. Array. @param last The last element to consider in the. Array. */ void quick. Sort(Item. Type the. Array[], int first, int last) Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 38 / 52

Quick Sort (4/8) SVVRL @ IM. NTU void quick. Sort(Item. Type the. Array[], int first, int last) { if (last - first + 1 < MIN_SIZE) insertion. Sort(the. Array, first, last); else { // Create the partition: S 1 | Pivot | S 2 int pivot. Index = partition(the. Array, first, last); // Sort subarrays S 1 and S 2 quick. Sort(the. Array, first, pivot. Index - 1); quick. Sort(the. Array, pivot. Index + 1, last); } // end if } // end quick. Sort Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 39 / 52

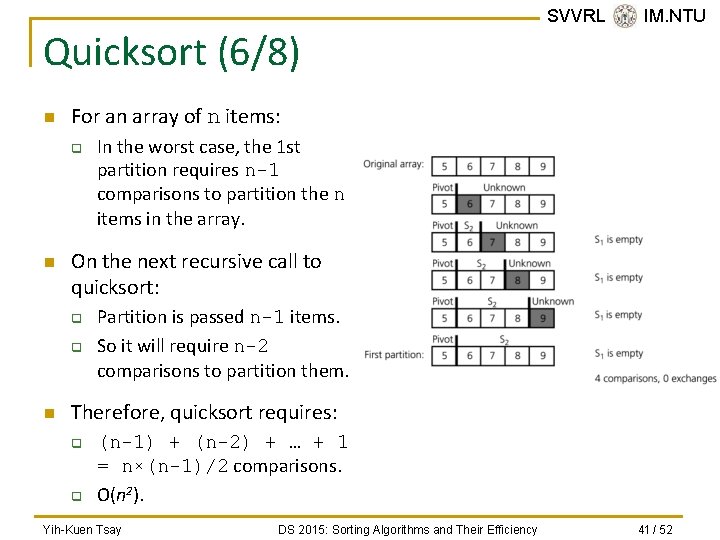
Quicksort (5/8) n n SVVRL @ IM. NTU The major effort in the quicksort function occurs during the partition step. Worst case: q The worst case behavior for quicksort occurs when the partition produces one sub-problem with n-1 elements and one with 0 elements. n n q And unbalanced partition arises in each recursive call. When the array is already sorted and the smallest item is chosen as the pivot. Because S 2 decreases in size by one at each recursive call to quicksort. The maximum number of recursive calls to quicksort will occur. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 40 / 52

Quicksort (6/8) n For an array of n items: q n In the worst case, the 1 st partition requires n-1 comparisons to partition the n items in the array. On the next recursive call to quicksort: q q n SVVRL @ IM. NTU Partition is passed n-1 items. So it will require n-2 comparisons to partition them. Therefore, quicksort requires: q q (n-1) + (n-2) + … + 1 = n×(n-1)/2 comparisons. O(n 2). Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 41 / 52

Quicksort (7/8) n SVVRL @ IM. NTU When S 1 and S 2 contain about the same number of items, there would be about log 2 n levels of recursive calls to quick. Sort, like in merge. Sort. n The average case of Quick sort is O(n × log 2 n). n Quicksort is usually extremely fast in practice. n Even if the worst case occurs, quicksort’s performance is acceptable for moderately large arrays. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 42 / 52

Quick Sort (8/8) SVVRL @ IM. NTU Source: FIGURE 11 -13 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 43 / 52

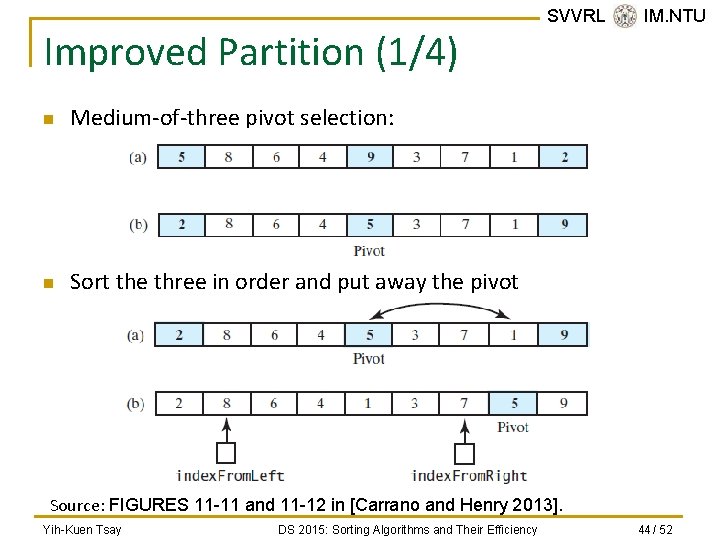
Improved Partition (1/4) n Medium-of-three pivot selection: n Sort the three in order and put away the pivot SVVRL @ IM. NTU Source: FIGURES 11 -11 and 11 -12 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 44 / 52

Improved Partition (2/4) SVVRL @ IM. NTU sort. First. Middle. Last(the. Array: Item. Array, first: integer, mid: integer, last: integer): void if (the. Array[first] > the. Array[mid] Interchange the. Array[first] and the. Array[mid] if (the. Array[mid] > the. Array[last] Interchange the. Array[mid] and the. Array[last] if (the. Array[first] < the. Array[mid] Interchange the. Array[first] and the. Array[mid] Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 45 / 52

Improved Partition (3/4) SVVRL @ IM. NTU // Partition with medium-of-three pivot selection. partition(the. Array: Item. Array, first: integer, last: integer): integer // Choose pivot and reposition it mid = first + (last – first) / 2 sort. First. Middle. Last(the. Array, first, mid, last) Interchange the. Array[mid] and the. Array[last – 1] pivot. Index = last - 1 pivot = the. Array[pivot. Index] // Determine the regions S 1 and S 2 index. From. Left = first + 1 index. From. Right = last – 2 done = false while (not done) { // Locate first entry on left that is ≥ pivot while (thearray[index. From. Left] < pivot) index. From. Left = index. From. Left + 1 // Locate first entry on right that is ≤ pivot while (thearray[index. From. Right] > pivot) Yih-Kuen Tsay DS 2015: Sorting Algorithms index. From. Right = index. From. Right –and 1 Their Efficiency 46 / 52

Improved Partition (4/4) SVVRL @ IM. NTU if (index. From. Left < index. From. Fight) { Interchange the. Array[index. From. Left] and the. Array[index. From. Fight] index. From. Left = index. From. Left + 1 index. From. Right = index. From. Right – 1 } else done = true } // Place pivot in proper position between S 1 and S 2, and // mark its new location Interchange the. Array[pivot. Index] and the. Array[index. From. Left] pivot. INdex = index. From. Left return pivot. Index Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 47 / 52

Radix Sort (1/4) SVVRL @ IM. NTU A radix sort of eight four-digit integers Source: FIGURE 11 -14 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 48 / 52

Radix Sort (2/4) n SVVRL @ IM. NTU The algorithm in pseudocode: // Sorts n d-digit integers in the array the. Array radix. Sort(the. Array: Item. Array, n: integer, d: integer): void for (j = d downto 1) { Initialize 10 groups to empty Initialize a counter for each group to 0 for (i = 0 through n – 1) { k = j-th digit of the Array[i] Place the. Array[i] at the end of group k Increase k-th counter by 1 } Replace the items in the. Array with all the items in group 0, followed by all the items in group 1, and so on. } Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 49 / 52

Radix Sort (3/4) n To sort n d-digit numbers, Radix sort requires: q q n n SVVRL @ IM. NTU n moves each time it forms groups. n moves to combine them into one group. Totally, 2×n×d moves. Thus, the Radix sort is O(n), if we treat d as a constant. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 50 / 52

Radix Sort (4/4) n Despite its efficiency, radix sort has some difficulties that make it inappropriate as a general-purpose sorting algorithm. q q q n SVVRL @ IM. NTU To sort integers, you need to accommodate 10 groups (0, 1, …, 9). Each group must be able to hold n strings. For large n, this requirement demands substantial memory! Radix sort is more appropriate when using chains than arrays to store data. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 51 / 52

SVVRL @ IM. NTU Comparison Note: Tree sort and Heap sort will be covered later in the course. Source: FIGURE 11 -15 in [Carrano and Henry 2013]. Yih-Kuen Tsay DS 2015: Sorting Algorithms and Their Efficiency 52 / 52