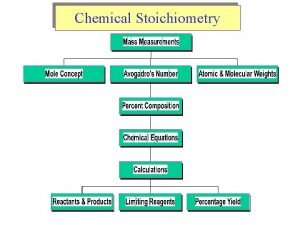
Stoichiometry Atomic Mass It is impossible to weigh

Stoichiometry

Atomic Mass • It is impossible to weigh a single atom, but one can easily establish the weight of an atom relative to another • We must establish a standard: – An atom of carbon-12 (six protons, six neutrons, six electrons) has a mass of exactly 12 atomic mass units (u) – Therefore, 1 atomic mass unit (u) is equivalent to exactly a twelfth of the mass of an atom of carbon 12 • If it is found that a hydrogen atom has only 8. 400% of the mass of a carbon-12 atom, the atomic mass of hydrogen must be: 0. 08400 x 12 u = 1. 008 u

Average Atomic Mass • Most natural elements have more than one isotope – e. g. ; there are two isotopes of carbon; carbon-12 (98. 89%) and carbon-13 (1. 11%, atomic mass = 13. 00335 u), and the average atomic mass is: (0. 9889)(12. 00000 u) + (0. 0111)(13. 00335) = 12. 01 u • Since carbon-12 is the dominant isotope, the average atomic mass is approximately 12 • N. B. 12. 01 u is an average value, and no single carbon atom has this mass, i. e. , it’s either 12. 00000 u or 13. 00335 u

Average Atomic Mass • The atomic masses of the two stable isotopes of boron, boron-10 (19. 78 %) and boron-11 (80. 22 %), are 10. 0129 u and 11. 0093 u, respectively. Calculate the average atomic mass of boron. • Solution: atomic mass of B = (0. 1978)(10. 0129 u) + (0. 8022)(11. 0093 u) = 10. 81 u

Avogadro’s Number • One mole describes a particular number of objects, just like a pair (2), a dozen (12), or a gross (144) • A mole is the number of carbon-12 atoms in exactly 12 g of carbon-12 • The current accepted value is 1 mole = 6. 022045 x 1023 particles

Molar Mass • The molar mass of an atom or molecule is the mass of one mole of these atoms or molecules • The molar mass of carbon-12 is thus exactly 12 g, by definition • The numerical value of the molar mass (in grams) for an atom is the same as the numerical value of the average atomic mass (in u) – e. g. ; For Na, the average atomic mass = 22. 99 u and the molar mass = 22. 99 g

The Mass of an Atom • We know that, by definition, 12 g de carbon-12 contains 6. 022045 x 1023 atoms of carbon-12 • The mass of a single atom of carbon-12 is therefore • A single atomic mass unit is 12 times smaller, and therefore 1 u = 1. 660565 x 10 -24 g, and 1 g = 6. 022045 x 1023 u

The Molar Mass of an Element and Avogadro’s Number • Example: What is the mass (in grams) of an atom of iodine? • Solution: – The molar mass of iodine = 126. 9 g/mol, therefore

Molecular Mass • The molecular mass is the sum of the atomic masses (in atomic mass units) of the atoms that make up a molecule • ex. ; the molecular mass of water is (2)(1. 008 u) + (1)(16. 00 u) = 18. 02 u • The molar mass of a molecule (in grams) has a numerical value equal to its average molecular mass (in atomic mass units) • e. g. ; the molar mass of water is 18. 02 g, and thus 18. 02 g of water contains one mole (or 6. 022045 x 1023 molecules) of water

Molecular Mass • Example: What is the molecular mass of methanol (CH 3 OH)? • Solution: molecular mass of CH 3 OH = (4)(1. 008 u) +(1)(12. 01 u) +(1)(16. 00 u) = 32. 04 u

Molar Mass • Example: Calculate the number of moles in 198 g of chloroform (CHCl 3). • Solution:

Mass Spectrometry • An electron beam ionizes the molecules, and a magnet affects the trajectory of the ions produced according to their charge : mass ratio • The signal produced by a particular ion is proportional to its abundance

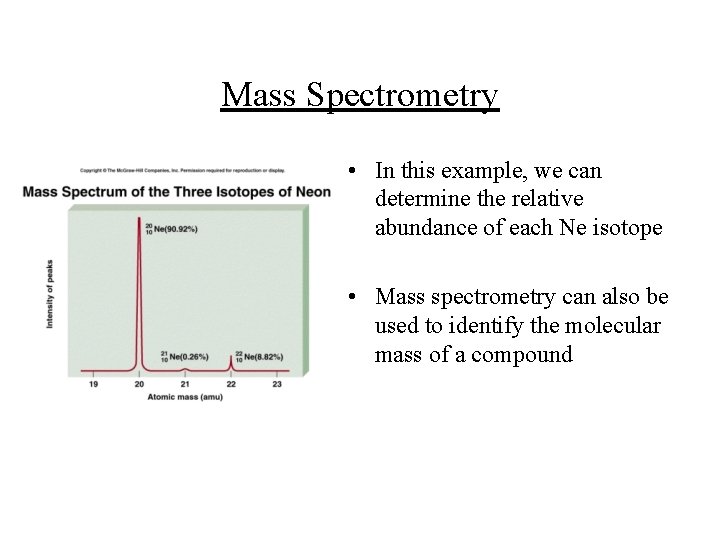
Mass Spectrometry • In this example, we can determine the relative abundance of each Ne isotope • Mass spectrometry can also be used to identify the molecular mass of a compound

Percent Composition • The percent composition is the mass percentage of each element contained within a compound • The percent composition allows us to establish the empirical formula of a compound – With the molecular mass, obtained from mass spectrometry, or the ideal gas law in the case of a gas, we can then determine the molecular formula

Percent Composition • Example: The percent composition of hydrogen peroxide is 5. 94% H and 94. 06% O. What is its empirical formula? If the molecular mass is 34. 02 u, what is the molecular formula? • Solution: – If we have 100 g of hydrogen peroxide, we’d have 94. 06 g of O and 5. 94 g of H, and therefore (94. 06 g)/(16. 00 g/mol) = 5. 88 mol of O and (5. 94 g)/(1. 008 g/mol) = 5. 89 mol of H – This gives a H: O ratio of about 1: 1, and therefore, the empirical formula is HO – If the molecular formula was HO, the molecular mass would be 17. 01 u (twice as small) – Therefore, the molecular formula is H 2 O 2

Percent Composition • Example: Determine the empirical formula of a compound with the following percent composition: 24. 75% K, 34. 77% Mn, and 40. 51% O. • Solution: – If we have 100 g of this compound, we’d have 24. 75 g of K, 34. 77 g of Mn, and 40. 51 g of O, or (24. 75 g)/(39. 10 g/mol) = 0. 6330 mol of K, (34. 77 g)/(54. 94 g/mol) = 0. 6329 mol of Mn, and (40. 51 g)/(16. 00 g/mol) = 2. 532 mol of O – This gives a K: Mn: O ratio of about 1: 1: 4 – Therefore, the empirical formula is KMn. O 4

• The percent composition of a compound is 38. 08% C, 31. 71% O, 25. 42% S, and 4. 79% H. The molecular mass of the compound is approximately 504. 6 g/mol. What is the empirical formula of this compound? What is the molecular formula? What is the mass (in g) of a molecule of this compound?

Balancing Chemical Equations • Once all of the reactants and products are known (this is not always trivial), we can balance the chemical equation so as to respect the law of conservation of mass • We can balance the equation by playing with the coefficients in front of each reactant or product (we can not play with the molecular formula!!!) • It is often easier to start balancing an element that appears in only one place on each side of the reaction

Balancing Chemical Equations • e. g. ; KCl. O 3 KCl + O 2 – K and Cl are balanced (for now) – We balance O 2 KCl. O 3 KCl + 3 O 2 – O is now balanced – K et Cl are not balanced anymore 2 KCl. O 3 2 KCl + 3 O 2 – The equation is now balanced

Balancing Chemical Equations • N. B. the chemical equations KCl. O 3 4 KCl. O 3 KCl + (3/2) O 2 4 KCl + 6 O 2 are both acceptable and balanced • However, it is common to balance equations using the smallest possible integers as coefficients

Balancing Chemical Equations • e. g. ; C 2 H 6 + O 2 CO 2 + H 2 O – None of the elements are balanced – We balance the C C 2 H 6 + O 2 2 CO 2 + H 2 O – We balance the H C 2 H 6 + O 2 2 CO 2 + 3 H 2 O – We balance the O C 2 H 6 + (7/2) O 2 2 CO 2 + 3 H 2 O – The equation is now balanced – We double the coefficients in order to obtain integers 2 C 2 H 6 + 7 O 2 4 CO 2 + 6 H 2 O

Balancing Chemical Equations • e. g. ; Fe 2 O 3 + CO Fe + CO 2

Calculating Masses of Reactants and Products • Stoichiometry is the study of the relationships between the masses of the reactants and products in a chemical reaction • If we know the amount of reactants (products), we can calculate the amount of products (reactants) that are formed (required) • To simplify the process, we use the moles method, i. e. , we work directly with the moles (rather than grams or liters)

Calculating Masses of Reactants and Products • For the reaction 2 CO(g) + O 2(g) 2 CO 2(g) at least two moles of CO (g) are needed to produce two moles of CO 2 (g) and at least one mole of O 2 (g ) is also necessary • In this example, we say that 2 mol of CO are stoichiometrically equivalent to 1 mol of O 2(g) as well as 2 mol of CO 2(g) • In the same way, we say that 1 mol of O 2(g) is stoichiometrically equivalent to 2 mol of CO 2(g)

The Mole Method • Step (1): Identify all of the reactants and products • Step (2): Balance the chemical equation • Step (3): Convert all the known quantities into moles • Step (4): Use the coefficients of the balanced chemical equation to determine the number of moles of the quantities sought • Step (5): If necessary, convert the number of the quantities sought into grams, litres, etc.

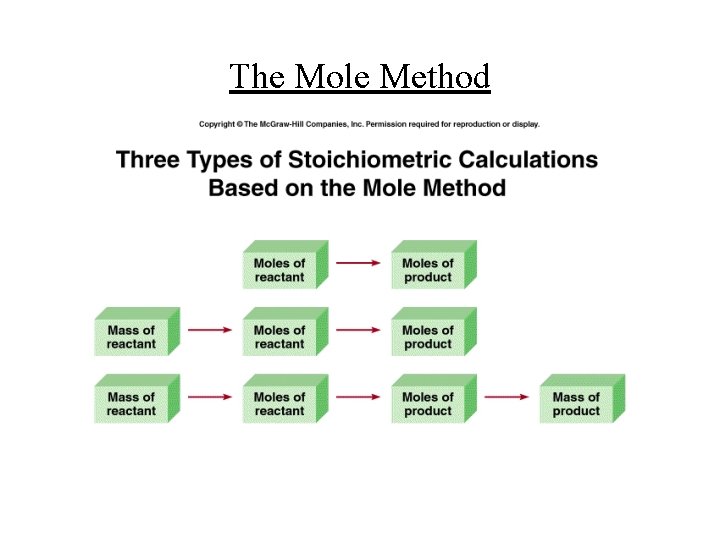
The Mole Method

The Mole Method • Example: The reaction between NO and O 2 is a key step in the formation of photochemical smog: 2 NO(g) + O 2(g) 2 NO 2(g) (a) How many moles of NO 2(g) are formed by the complete reaction of 0. 254 mol of O 2(g)? (b) What mass, in grams, of NO 2(g) is obtained by the complete reaction of 1. 44 g of NO(g)?

The Mole Method • Solution: (a) The equation is already balanced and we know that et 0. 254 mol of O 2(g) reacts. Thus, we produce twice as much NO 2. We produce 0. 508 mol. (b) 1. 44 g of NO is (1. 44 g)/(14. 01 g/mol + 16. 00 g/mol) = 0. 0480 mol of NO This will produce 0. 0480 mol of NO 2. This has a mass of (0. 0480 mol)x [14. 01 g/mol + (2)(16. 00 g/mol)] = 2. 21 g

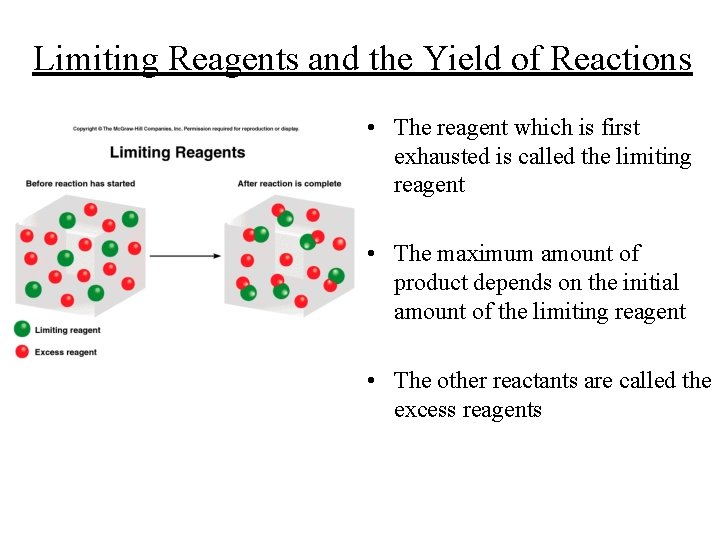
Limiting Reagents and the Yield of Reactions • The reagent which is first exhausted is called the limiting reagent • The maximum amount of product depends on the initial amount of the limiting reagent • The other reactants are called the excess reagents

Limiting Reagents and the Yield of Reactions • e. g. ; For the reaction – – – S(l) + 3 F 2(g) SF 6(g) We have 4 moles of S and 9 moles of F 2 4 moles of S will react with 12 moles of F 2 But we only have 9 moles of F 2 The F 2 will be used up before all of the S can react The F 2 is the limiting reagent N. B. We arrive at the same conclusion when saying that the 9 moles of F 2 will react with only 3 moles of S, thus leaving 1 mole of S in excess – 3 moles of SF 6 is produced

• What mass of POCl 3 is produced when 790. 0 g of PCl 3(l), 345. 0 g of Cl 2(g), and 265. 0 g of P 4 O 10(s) reacts together in the following fashion? 6 PCl 3(l) + 6 Cl 2(g) + P 4 O 10(s) → 10 POCl 3(l)