Stoichiometry The MoleQuantifying Equations Atomic Mass The mass

Stoichiometry The Mole—Quantifying Equations

Atomic Mass � The mass of a single atom is far too small in grams to use conveniently. � Chemists use the unit called the unified atomic mass unit (amu) or Dalton (Da). � Definition of amu is exactly 1/12 the mass of an atom of 12 C • Amu (Da) = 1. 660539 x 10 -24 g

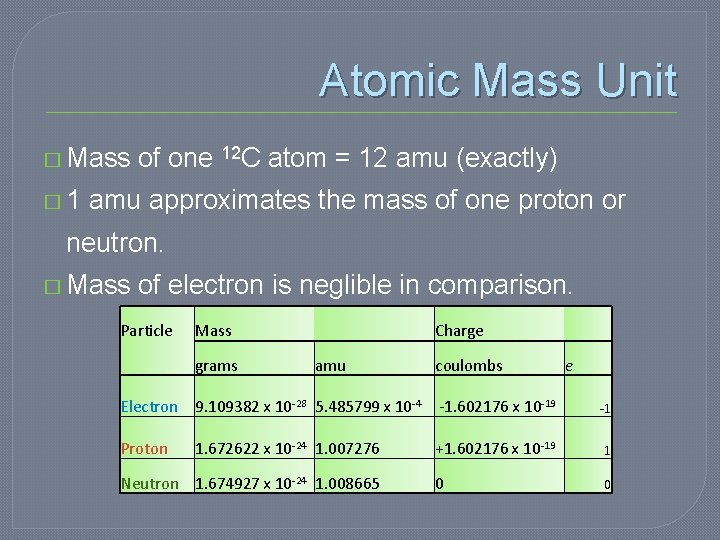
Atomic Mass Unit � Mass of one 12 C atom = 12 amu (exactly) � 1 amu approximates the mass of one proton or neutron. � Mass of electron is neglible in comparison. Particle Mass Charge grams amu coulombs e Electron 9. 109382 x 10 -28 5. 485799 x 10 -4 -1. 602176 x 10 -19 Proton 1. 672622 x 10 -24 1. 007276 Neutron 1. 674927 x 10 -24 1. 008665 -1 +1. 602176 x 10 -19 1 0 0

Mass Number � Elements differ in the number of protons in their atoms. • The atomic number Z � All atoms of a given element have the same number of protons. � Number of electrons equals protons. � Number of neutrons = N � Mass Number (A) = Z + N � Mass number is the total number of nucleons.

Mass for Specific Elements �Why do all element not have atomic mass number listed in the periodic table that is not a whole number or very close to it? �Are all atoms of an element the same?

Isotopes � Isotopes are atoms with the same atomic number, but different mass number. � The larger mass size is due to the difference in the number of neutrons that an atom contains. Although mass numbers are whole numbers, the actual masses of individual atoms are never whole numbers (except for carbon-12). This explains how Lithium can have an atomic mass of 6. 941 Da.

Calculating Average Atomic Mass � The atomic masses on the periodic table take these isotopes into account, weighing them based on their abundance in nature, therefore, more weight is given to the isotopes that occur most frequently in nature. Average mass of the element E is defined as: �m(E) = ∑(m(In)*p(In)) � where ∑ represents a n-times summation over all isotopes In of element E, and p(I) represents the relative abundance of the isotope I.

Atomic mass based on isotopes Find the average atomic mass of Boron Mass and abundance of Boron isotopes n isotope In mass m (Da) isotopic abundance p 1 10 B 10. 013 0. 199 2 11 B 11. 009 0. 801 Solution: The average mass of Boron is: m(B) = (10. 013 Da)(. 199) + (11. 009 Da)(. 801) = 1. 99 Da + 8. 82 Da = 10. 81 Da

Molecular Mass • Molecular mass: sum of atomic masses of all atoms in a molecule • Formula mass: sum of atomic masses of all atoms in a formula unit of any compound, molecular or ionic.

Mole Puns can you dig it? � What is a mole's favorite movie? The Green Mole � What do you get when you have a bunch of moles acting like idiots? Moleasses � What line from Shakespeare do high school moles have to memorize? “To mole or not to mole, that is the question. ” � How much does Avogadro exaggerate? He makes mountains out of molehills. � What element do moles love to study in chemistry? Moleybdenum

Calculate the Molecular Mass � Copper (II) Nitrate Cu(NO 3)2 • 63. 5 + [(14 + {3 x 16}) x 2] = 187. 5 g � Ca 3(PO 4)2 3 moles of Ca 2 moles of P 2 x 4 moles of O. � 1 mole of Ca is 40. 08 g, so 3 moles are 120. 24 g � 1 mole of P is 30. 9738 g, so 2 moles are 61. 9476 g � 1 mole of O is 15. 9994 g, so 8 moles are 127. 9952 g � 1 mole of Ca 3(PO 4)2 is 310. 18 g

Molecular Mass Ratio �From a balanced equation, the coefficients define the ratio of reactants needed for the products that result from the reaction. �Counting atoms is impractical. �Use a mass ratio: • to predict mass of products in ideal conditions. • to calculate the percentage yield in actual conditions. • to obtain the mass of each reactant needed.

Example � Balanced equation: � C 2 H 4 + HCl 1 : 1 28. 0 : 35. 5 C 2 H 5 Cl yields 1 for ratio of molecules 64. 5 for mass ratio Ethylene: Atomic mass of 2 C = 2 x 12. 0 amu = 24. 0 amu Atomic mass of 4 H = 4 x 1. 0 amu = 4. 0 amu Molecular mass of C 2 H 4 = 28. 0 amu Hydrogen chloride: at. mass of H = 1. 0 amu at. Mass of Cl = 35. 5 amu Molecular mass of HCl = 36. 5 amu Ethyl chloride: at. mass of 2 C = 2 x 12. 0 amu = 24. 0 amu at. mass of 5 H = 5 x 1. 0 amu = 5. 0 amu at. mass of Cl = 35. 5 amu Molecular mass of C 2 H 5 Cl = 64. 5 amu

Try these: � 1. sodium fluoride � 2. potassium hydroxide � 3. copper (I) chloride � 4. manganese (IV) oxide � 5. calcium sulfate � 6. magnesium phosphate

Amadeo Avogadro �Amadeo Avogadro was an Italian physics professor who proposed in 1811 that equal volumes of different gases at the same temperature contain equal numbers of molecules.

History—or how did they find that number? ? ? � If Avogadro’s hypothesis is true, then atomic weights for gases can be derived by weighing equal volumes of different gases (Cannizzaro). � Johan Loschmidt (HS teacher) took the idea and calculated the size of a molecule of air. He developed an estimate for the number of molecules in a given volume of air. � These three ideas together lead to the number named for Avogadro. Loschmidt was the first to calculate this number.

Avogadro’s Number � 1 mole of a substance, NA = 6. 02214179(30)× 1023 is known as the Avogadro constant. �For calculations please use 6. 02 x 1023 �http: //www. youtube. com/watch? v=Hj 83 o. R Hdezc&safety_mode=true&persist_safety_ mode=1&safe=active

Mole is just a number �Definition: A mole is the amount of substance that contains as many elementary particles as there atoms in exactly 12 grams of carbon-12 (12 C). � 1 Mole = 6. 022045 x 1023 particles (atoms, molecules, ions, electrons, apples, wads of gum, elephants) = NA particles ~100 million x 100 million

Conversion factors � 6. 022045 x 1023 whatever kind of particles per mole �One mole of common substances: • Ca. CO 3 : 100. 09 g • Oxygen: 32. 00 g • Copper: 63. 55 g • Water: 18. 02 g

2 H 2 (g) + O 2 (g) → 2 H 2 O(g) 2 dozen H 2 molecules react with exactly 1 dozen O 2 molecules to give exactly 2 dozen H 2 O molecules. 2 moles of H 2 molecules react with exactly 1 mole of O 2 molecules to give exactly 2 moles of H 2 O molecules. Why do we do this? Because these last sizes are in the gram range and easy to weigh. Conventions: 1 mole of 12 C atoms weighs 12 g exactly. 1 atom of 12 C weighs 12 amu exactly. (amu = atomic mass unit = ~mass of a proton or neutron)

2 H 2 (g) + O 2 (g) → 2 H 2 O(g) 2 moles of H 2 molecules react with exactly 1 mole of O 2 molecules to give exactly 2 moles of H 2 O molecules. 2 moles of H 2 molecules 4 x 1. 008 g = 4. 032 g react with exactly 1 mole of O 2 molecules 2 x 15. 994 g = 31. 988 g to produce exactly 2 moles of H 2 O molecules 2(2 x 1. 008 g + 15. 994 g) = 36. 03 g Sum of reactants = Sum of products Law of Conservation of Mass

Number – mass relationships Mole – mass relationships 12 red marbles @ 7 g each = 84 g 12 yellow marbles @4 e each=48 g 55. 85 g Fe = 6. 022 x 1023 atoms Fe 32. 07 g S = 6. 022 x 1023 atoms S

Mole—Mass Relationships Element Atomic Mass Molar Mass Number of Atoms 1 atom of H = 1. 008 amu 1. 008 g = 6. 022045 x 1023 atoms 1 atom of S = 32. 07 amu 32. 07 g = 6. 022045 x 1023 atoms 1 atom of O = 15. 994 amu 15. 994 g = 6. 022045 x 1023 atoms 1 molecule O 2 (15. 994 x 2) 32. 00 amu 32. 00 g = 6. 022045 x 1023 atoms 1 molecule S 8 (32. 07 x 8) 256. 56 amu 256. 56 g = 6. 022045 x 1023 atoms

Calculating the Number of Moles and Atoms in a Given Mass of Element – Class Problem: Tungsten (W) is the element used as the filament in light bulbs, and has the highest melting point of any element, 3680 o. C. How many moles of tungsten, and atoms of the element, are contained in a 35. 0 mg sample of the metal? Plan: Convert Mass to Moles Convert Moles to Atoms

Calculation Solution: Moles of W = 35. 0 x 10 -3 g W x 1 mol W = 0. 00019032 mol 183. 9 g W Moles of W = 1. 90 x 10 -4 mol No. of W atoms = 1. 90 x 10 -4 mol W x 6. 022 x 1023 atoms 1 mole of W = 1. 15 x 1020 atoms of Tungsten

Molecular Mass—Molar Mass (M) The molecular mass of a compound expressed in amu is numerically the same as the mass of one mole of the compound expressed in grams , called its molar mass.

Calculate the Molecular Mass of Glucose: C 6 H 12 O 6 �Carbon— 6 x 12. 01 amu = 72. 06 amu �Hydrogen— 12 x 1. 008 amu = 12. 096 amu �Oxygen— 6 x 15. 994 amu = 95. 964 amu 180. 12 amu

Calculate the Molar Mass of Glucose: C 6 H 12 O 6 � Carbon— 6 x 12. 01 g/mol = 72. 06 g/mol � Hydrogen— 12 x 1. 008 g/mol = 12. 096 g/mol � Oxygen— 6 x 15. 994 g/mol = 95. 964 g/mol 180. 12 g/mol

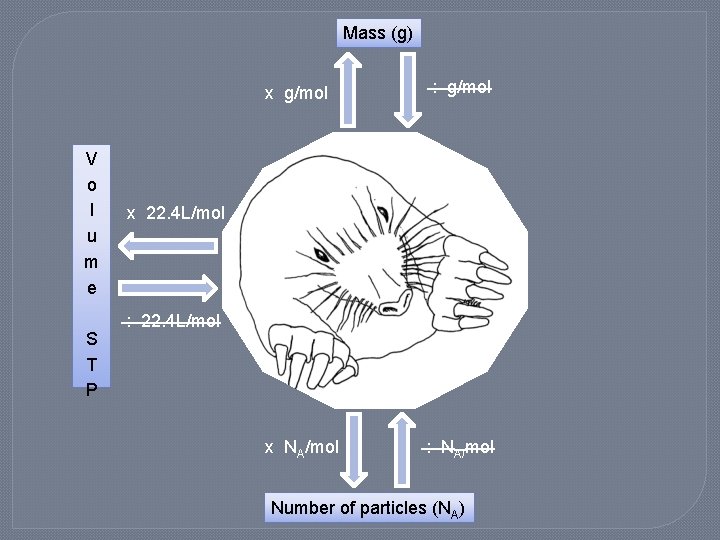
Conversions �Go from mass (g) to moles �Go from moles to particles (NA) �Go from moles to volume of gas (L) �Go from moles to mass (g)

Mass (g) x g/mol V o l u m e S T P : g/mol x 22. 4 L/mol : 22. 4 L/mol x NA/mol : NA/mol Number of particles (NA)

Percent Composition �For a compound, the percent composition for a specific element is the fraction of the compound mass that came from that element. A n. B m %A = n(A g/mol) x 100 An. Bm g/mol

Mass Fraction and Mass % Mass of Red Balls = Mass Fraction Red = Mass % Red = 3. 0 g/ball x 3 balls = 9 g 9. 0 g/16. 0 g total = 0. 56 x 100% = 56% red Mass Fraction Purple = 2. 0 g/ball x 2 balls = 0. 25 16 g total 0. 25 x 100 = 25% purple Mass Fraction Yellow = 1. 0 g/ball x 3 balls = 3. 0 g 16 g total 0. 19 x 100 = 19% yellow Check: 56% + 25% + 19% = 100%

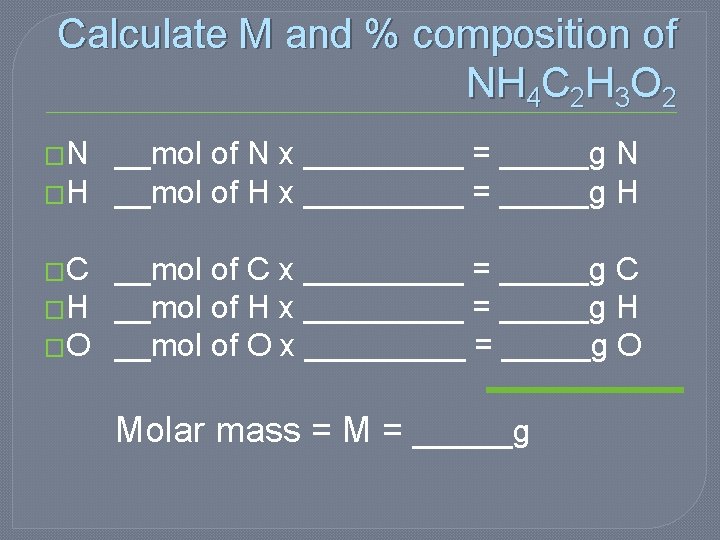
Calculate M and % composition of NH 4 C 2 H 3 O 2 �N __mol of N x _____ = _____g N �H __mol of H x _____ = _____g H �C __mol of C x _____ = _____g C �H __mol of H x _____ = _____g H �O __mol of O x _____ = _____g O Molar mass = M = _____g

Calculate M and % composition of NH 4 C 2 H 3 O 2 � N 1 mol of N x 14. 01 g/mol = 14. 01 g N � H 7 mol of H x 1. 008 g/mol = 7. 056 g H � C 2 mol of C x 12. 011 g/mol = 24. 022 g C � O 2 mol of O x 15. 994 g/mol = 31. 988 g Molar mass = M = 77. 076 g NH 4 C 2 H 3 O 2 � %N = 14. 01 g N/77. 076 g = 18. 18% � %H = 7. 056 g H/77. 076 g = 9. 15% � %C = 24. 022 g C/77. 076 g = 31. 17% � %O = 31. 988 g O/77. 076 g = 41. 50% 100. 00%

Empirical Formula �Empirical Formula - A formula that gives the simplest whole-number ratio of atoms in a compound. �Once the empirical formula is found, the molecular formula for a compound can be determined if the molar mass of the compound is known. �Many compounds can share the same empirical formula. Alkanes are Cn. H 2 n +2

Determining Empirical Formula � Start with the number of grams of each element, given in the problem. • If percentages are given, assume that the total mass is 100 grams so that the mass of each element = the percent given. � � � Convert the mass of each element to moles using the molar mass from the periodic table. Divide each mole value by the smallest number of moles calculated. Round to the nearest whole number. This is the mole ratio of the elements and is represented by subscripts in the empirical formula. • If the number is too far to round (x. 1 ~ x. 9), then multiply each solution by the same factor to get the lowest whole number multiple. �e. g. If one solution is 1. 5, then multiply each solution in the problem by 2 to get 3. �e. g. If one solution is 1. 25, then multiply each solution in the problem by 4 to get 5.

Example �A compound was analyzed and found to contain 13. 5 g Ca, 10. 8 g O, and 0. 675 g H. What is the empirical formula of the compound?

First step �Find the moles for each element

Find the ratio of moles � Divide each by the smallest number of moles present. Round to nearest whole number.

Finding the Formula �This is the mole ratio of the elements and is represented by subscripts in the empirical formula. Ca— 1 O— 2 H— 2 Therefore Ca. O 2 H 2 or with the correct formula, Ca(OH)2.

Nutrasweet �Nutra. Sweet is 57. 14% C, 6. 16% H, 9. 52% N, and 27. 18% O. Calculate the empirical formula of Nutra. Sweet and find the molecular formula. (The molar mass of Nutra. Sweet is 294. 30 g/mol)

Start with the number of grams of each element, given in the problem. �If percentages are given, assume that the total mass is 100 grams so that the mass of each element = the percent given. � 57. 14% C, 6. 16% H, 9. 52% N, and 27. 18% O.

Convert the mass of each element to moles using the molar mass from the periodic table. �Use the conversion factor: g/mol and divide or multiply by 1/g/mol.

Divide each mole value by the smallest number of moles calculated. Round to the nearest whole number. � Select the smallest number of moles to divide each element (moles). Smallest one will equal 1.

Mole Ratio of Elements � This is the mole ratio of the elements and is represented by subscripts in the empirical formula. • If the number is too far to round (x. 1 ~ x. 9), then multiply each solution by the same factor to get the lowest whole number multiple.

Molecular Formula �Now, we can find the molecular formula by finding the mass of the empirical formula and setting up a ratio:

Empirical Formula Experiment � A sample of a pure oxide of nickel was analyzed by heating to drive off the oxygen. A team of students weighed an empty test tube, recording a mass of 32. 064 g. After adding a sample to the tube, they measured a total mass of 33. 076 g. The team then heated the sample in an atmosphere of natural gas reducing it to pure metal. The final mass after two heatings was 32. 785 g for the tube and the metal residue. Perform calculations necessary to find results below, showing all of your work. • • • � � Mass of nickel oxide sample Mass of nickel present in sample Mass of oxygen present in sample Mass percent of nickel Mass percent of oxygen Determine the empirical formula of the oxide of nickel, showing your work clearly. Name the compound according to IUPAC conventions.

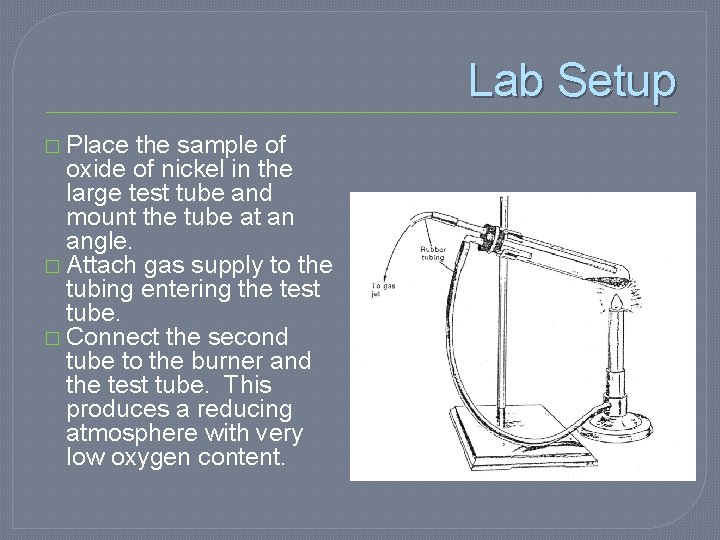
Lab Setup � Place the sample of oxide of nickel in the large test tube and mount the tube at an angle. � Attach gas supply to the tubing entering the test tube. � Connect the second tube to the burner and the test tube. This produces a reducing atmosphere with very low oxygen content.

What are the possible formulas? �Find the possible cations that nickel forms. �Write balanced equations. �What are the molar ratios of reactant to elemental nickel that you would expect to find? (Molar conversions) �Predict which ionic unit formula will result in describing the reaction. �Calculate the formula.

Calculations