Unit 6 Stoichiometry Chapter 9 Stoichiometry CHAPTER 9

Unit 6 Stoichiometry Chapter 9

Stoichiometry CHAPTER 9

Chapter 9 – Section 1: Introduction to Stoichiometry What is Stoichiometry? • Stoichiometry is the branch of chemistry that deals with the mass relationships of elements in a chemical reaction. • Stoichiometry calculations always start with a balanced chemical equation.

Chapter 9 – Section 1: Introduction to Stoichiometry Mole Ratio • A mole ratio is a conversion factor that relates the amounts in moles of any two substances involved in a chemical reaction Example: 2 Al 2 O 3(l) → 4 Al(s) + 3 O 2(g) Mole Ratios: 2 mol Al 2 O 3 4 mol Al 2 O 3 3 mol O 2 4 mol Al 3 mol O 2

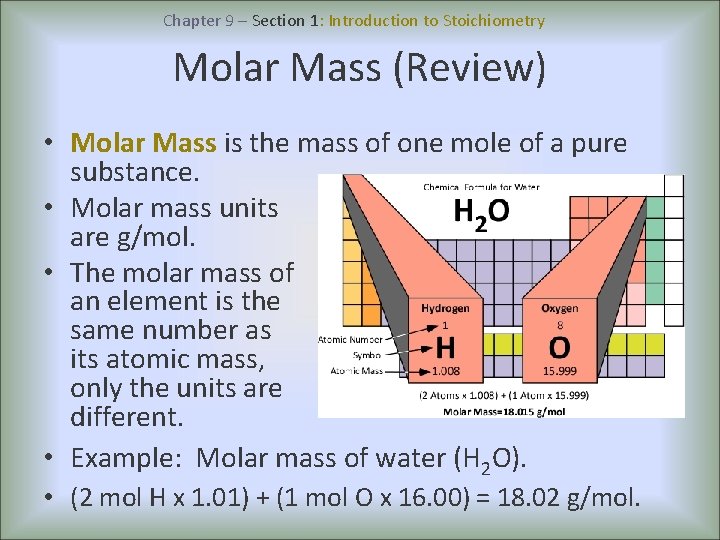
Chapter 9 – Section 1: Introduction to Stoichiometry Molar Mass (Review) • Molar Mass is the mass of one mole of a pure substance. • Molar mass units are g/mol. • The molar mass of an element is the same number as its atomic mass, only the units are different. • Example: Molar mass of water (H 2 O). • (2 mol H x 1. 01) + (1 mol O x 16. 00) = 18. 02 g/mol.

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mole to Mole Conversions • Using the mole ratio, you can convert from moles of one substance to moles of any other substance in a chemical reaction. Example: • For the reaction N 2 + 3 H 2 → 2 NH 3, how many moles of H 2 are required to produce 12 moles of NH 3? This is what we’re given: Use mole ratio as a conversion factor 12 mol NH 3 x 3 mol H 2 = 18 mol H 2 2 mol NH 3

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mole/Mole Conversions Sample Problem 1 In a spacecraft, the CO 2 exhaled by astronauts can be removed by the following reaction with Li. OH: CO 2(g) + 2 Li. OH(s) → Li 2 CO 3(s) + H 2 O(l) How many moles of lithium hydroxide are required to react with 20 mol CO 2, the average amount exhaled by a person each day? Solution: Given Conversion factor 20 mol CO 2 x 2 mol Li. OH = 40 mol Li. OH 1 mol CO 2

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mole to Mass Conversions • To convert from moles of one substance to grams of another, you need 2 conversion factors: 1. mole ratio. 2. molar mass of the unknown. • To set up your conversion factor, always put the units you have on the bottom and the units you need on the top.

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mole to Mass Conversions (continued) Example: Given the equation: 2 Mg(s) + O 2(g)→ 2 Mg. O(s), Calculate the mass in grams of magnesium oxide which is produced from 2. 00 mol of magnesium. Given 2. 00 mol Mg x 1 st C. F. Mole Ratio 2 nd C. F. Molar Mass of the Unknown 2 mol Mg. O x 40. 3 g Mg. O = 80. 6 g Mg. O 2 mol Mg 1 mol Mg. O

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mass to Mole Conversions • To convert from grams of one substance to moles of another, you need 2 conversion factors: 1. molar mass of the given. 2. mole ratio. • Mass to mole conversion factors are the inverse of mole to mass conversion factors.

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mass to Mole Conversions (continued) Example: Given the equation: 2 Hg. O(s) → 2 Hg(s) + O 2(g), How many moles of Hg. O are needed to produce 125 g of O 2? Given 125 g O 2 1 st C. F. Molar Mass of the Given x 1 mol O 2 32 g O 2 2 nd C. F. Mole Ratio x 2 mol Hg. O 1 mol O 2 = 7. 81 mol Hg. O

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mole/Mass Conversions Sample Problem 1 The balanced equation for photosynthesis is as follows: 6 CO 2(g) + 6 H 2 O(l) → C 6 H 12 O 6(s) + 6 O 2(g) What mass, in grams, of glucose (C 6 H 12 O 6) is produced when 3. 00 mol of water react with carbon dioxide? Solution: Given 1 st C. F. Mole Ratio 2 nd C. F. Molar Mass of the Unknown 1 180. 2 mol C H O g C 6 H 12 O 6 6 12 6 x x 3. 00 mol H 2 O = 90. 1 g 6 mol H 2 O 1 mol C 6 H 12 O 6

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mole/Mass Conversions Sample Problem 2 The first step in the industrial manufacture of nitric acid is the catalytic oxidation of ammonia: 4 NH 3(g) + 5 O 2(g) → 4 NO(g) + 6 H 2 O(g) If the reaction is run using 824 g NH 3 and excess oxygen, how many moles of NO are formed? st C. F. 1 Solution: Molar Mass of the Given 1 mol NH 3 x x 824 g NH 3 17. 0 g NH 3 2 nd C. F. Mole Ratio 4 mol NO 4 mol NH 3 = 48. 5 mol NO

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mass to Mass Conversions • To convert from grams of one substance to grams of another, you need 3 conversion factors: 1. molar mass of the given. 2. mole ratio. 3. molar mass of the unknown.

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mass to Mass Conversions (continued) Example: Given the equation: 2 Hg. O(s) → 2 Hg(s) + O 2(g), How many grams of Hg. O are needed to produce 45 g of O 2? 1 st C. F. Given Molar Mass of the Given 1 mol O 2 x 45 g O 2 32 g O 2 3 rd C. F. Molar Mass of 2 nd C. F. Mole Ratio the Unknown x 2 mol Hg. O x 216. 6 g Hg. O = 609. 2 g 1 mol O 2 1 mol Hg. O

Chapter 9 – Section 2: Ideal Stoichiometric Calculations Mass/Mass Conversions Sample Problem 1 Tin(II) fluoride, Sn. F 2, is used in some toothpastes. It is made by the following reaction : Sn(s) + 2 HF(g) → Sn. F 2(s) + H 2(g) How many grams of Sn. F 2 are produced from the reaction of 30. 0 g HF with Sn? Solution: 1 st C. F. 3 rd C. F. Molar Mass 2 nd C. F. Molar Mass of Given of the Given Mole Ratio the Unknown 30. 0 g HF x 1 mol Sn. F 2 x 156. 7 g Sn. F 2 = 117. 5 g Sn. F 2 20. 0 g HF 2 mol HF 1 mol Sn. F 2

Chapter 9 – Section 3: Limiting Reactants and Percentage Yield Limiting Reactants • When combining 2 or more different things to make a product, you have to stop when one of the things is used up. • For example, no matter how many tires there are, if there are only 8 car bodies, then only 8 cars can be made.

Chapter 9 – Section 3: Limiting Reactants and Percentage Yield Limiting Reactants (continued) • The limiting reactant is the reactant that limits the amount of product formed. • The excess reactant is the substance that is not used up completely. • Once the limiting reactant is used up, a chemical reaction will stop.

Chapter 9 – Section 3: Limiting Reactants and Percentage Yield Limiting Reactants (continued) Example: Silicon dioxide reacts with hydrogen fluoride according to the following equation: The limiting Si. O 2(s) + 4 HF(g) → Si. F 4(g) + 2 H 2 O(l) reactant If 6. 0 mol HF is added to 4. 5 mol Si. O 2, which makes the is the limiting reactant? Mole ratio C. F. least product. Set up 2 6 mol HF x equations, one for each given: 4. 5 mol Si. O 2 x 1 mol Si. F 4 = 1. 5 mol Si. F 44 4 mol HF Limiting Reactant is HF 1 mol Si. F 4 = 4. 5 mol Si. F 4 1 mol Si. O 2

Chapter 9 – Section 3: Limiting Reactants and Percentage Yield Limiting Reactants Sample Problem 1 According to the following reaction : CS 2(l) + 3 O 2(g) → CO 2(g) + 2 SO 2(g) a. If 1 mol CS 2 reacts with 1 mol O 2, identify the limiting reactant. 1 mol CS 2 x 2 mol SO 2 = 2 mol SO 2 Limiting 1 mol CS 2 Reactant is O 2 1 mol O 2 x 2 mol SO 2 = 0. 67 mol SO 2 0. 67 mol SO Mol of excess 3 mol O 2 reactant that b. How many moles of excess reactant remain? Work 0. 67 mol SO 2 x 1 mol CS 2 = 0. 33 mol CS 2 was used up backwards from 2 mol SO 2 Moles actual mol of remaining product formed 1 mol CS 2 - 0. 33 mol CS 2 = 0. 67 mol CS 2

Chapter 9 – Section 3: Limiting Reactants and Percentage Yield • The theoretical yield is the maximum amount of product that can be produced from a given amount of reactant (found with stoichiometry). • The actual yield of a product is the measured amount of that product obtained from a reaction (given in problem). • The percentage yield is the ratio of the actual yield to theoretical yield, multiplied by 100.

Chapter 9 – Section 3: Limiting Reactants and Percentage Yield (continued) Example: Given the following equation: C 6 H 6 (l) + Cl 2(g) → C 6 H 5 Cl(l) + HCl(g) When 36. 8 g C 6 H 6 react with excess Cl 2, the actual yield of C 6 H 5 Cl is 38. 8 g. What is the percentage yield of C 6 H 5 Cl? Set up a mass to mass conversion This is the Theoretical Yield 36. 8 g C 6 H 6 x 1 mol C 6 H 5 Cl x 112. 5 g C 6 H 5 Cl = 53. 1 g 78. 0 g C 6 H 6 1 mol C 6 H 5 Cl Actual x 100 38. 8 g C 6 H 5 Cl x 100 Percent = 73. 1% Now use = = Theoretical 53. 1 g C 6 H 5 Cl the formula Yield

Chapter 9 – Section 3: Limiting Reactants and Percentage Yield Sample Problem 1 According to the following reaction : CO(g) + 2 H 2(g) → CH 3 OH(l) If the typical yield is 80%, what mass of CH 3 OH should be expected if 75. 0 g of CO reacts with excess hydrogen gas? Set up a mass to mass conversion This is the Theoretical Yield 75. 0 g CO x 1 mol CH 3 OH x 32. 0 g CH 3 OH = 85. 7 g 28. 0 g CO 1 mol CH 3 OH Multiply theoretical yield by percentage to get actual yield 85. 7 g CH 3 OH x 80% = 68. 6 g CH 3 OH