STATISTICS INFORMED DECISIONS USING DATA Fifth Edition Chapter














































































- Slides: 103

STATISTICS INFORMED DECISIONS USING DATA Fifth Edition Chapter 3 Numerically Summarizing Data Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency Learning Objectives 1. Determine the arithmetic mean of a variable from raw data 2. Determine the median of a variable from raw data 3. Explain what it means for a statistic to be resistant 4. Determine the mode of a variable from raw data Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 1 Determine the Arithmetic Mean of a Variable from Raw Data (1 of 9) The arithmetic mean of a variable is computed by adding all the values of the variable in the data set and dividing by the number of observations. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 1 Determine the Arithmetic Mean of a Variable from Raw Data (2 of 9) The population arithmetic mean, μ (pronounced “mew”), is computed using all the individuals in a population. The population mean is a parameter. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 1 Determine the Arithmetic Mean of a Variable from Raw Data (3 of 9) The sample mean is a statistic. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 1 Determine the Arithmetic Mean of a Variable from Raw Data (4 of 9) If x 1, x 2, …, x. N are the N observations of a variable from a population, then the population mean, µ, is Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 1 Determine the Arithmetic Mean of a Variable from Raw Data (5 of 9) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

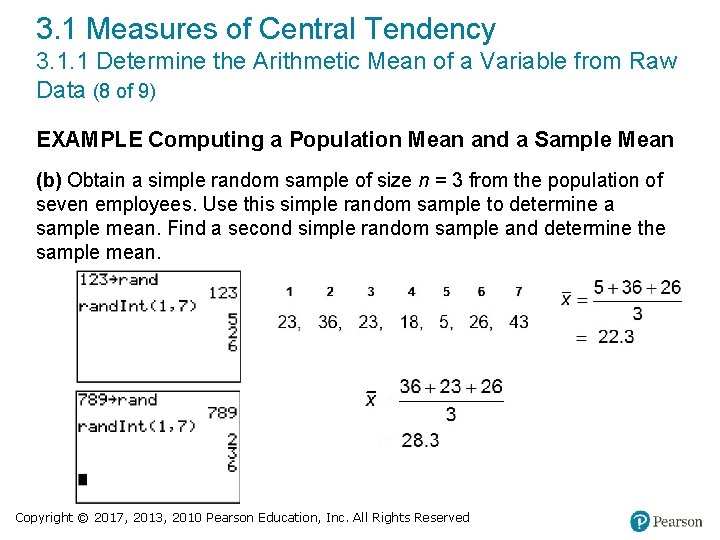
3. 1 Measures of Central Tendency 3. 1. 1 Determine the Arithmetic Mean of a Variable from Raw Data (6 of 9) EXAMPLE Computing a Population Mean and a Sample Mean The following data represent the travel times (in minutes) to work for all seven employees of a start-up web development company. 23, 36, 23, 18, 5, 26, 43 (a) Compute the population mean of this data. (b) Then take a simple random sample of n = 3 employees. Compute the sample mean. Obtain a second simple random sample of n = 3 employees. Again compute the sample mean. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 1 Determine the Arithmetic Mean of a Variable from Raw Data (7 of 9) EXAMPLE Computing a Population Mean and a Sample Mean (a) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 1 Determine the Arithmetic Mean of a Variable from Raw Data (8 of 9) EXAMPLE Computing a Population Mean and a Sample Mean (b) Obtain a simple random sample of size n = 3 from the population of seven employees. Use this simple random sample to determine a sample mean. Find a second simple random sample and determine the sample mean. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 1 Determine the Arithmetic Mean of a Variable from Raw Data (9 of 9) IN CLASS ACTIVITY Population Mean versus Sample Mean Treat the students in the class as a population. All the students in the class should determine their pulse rates. a) Compute the population mean pulse rate. b) Obtain a simple random sample of n = 4 students and compute the sample mean. Does the sample mean equal the population mean? c) Obtain a second simple random sample of n = 4 students and compute the sample mean. Does the sample mean equal the population mean? d) Are the sample means the same? Why? Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 2 Determine the Median of a Variable from Raw Data (1 of 5) The median of a variable is the value that lies in the middle of the data when arranged in ascending order. We use M to represent the median. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 2 Determine the Median of a Variable from Raw Data (2 of 5) Steps in Finding the Median of a Data Set Step 1 Arrange the data in ascending order. Step 2 Determine the number of observations, n. Step 3 Determine the observation in the middle of the data set. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 2 Determine the Median of a Variable from Raw Data (3 of 5) Steps in Finding the Median of a Data Set Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 2 Determine the Median of a Variable from Raw Data (4 of 5) EXAMPLE Computing a Median of a Data Set with an Odd Number of Observations The following data represent the travel times (in minutes) to work for all seven employees of a start-up web development company. 23, 36, 23, 18, 5, 26, 43 Determine the median of this data. Step 1: 5, 18, 23, 26, 36, 43 Step 2: There are n = 7 observations. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 2 Determine the Median of a Variable from Raw Data (5 of 5) EXAMPLE Computing a Median of a Data Set with an Even Number of Observations Suppose the start-up company hires a new employee. The travel time of the new employee is 70 minutes. Determine the median of the “new” data set. 23, 36, 23, 18, 5, 26, 43, 70 Step 1: 5, 18, 23, 26, 36, 43, 70 Step 2: There are n = 8 observations. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 3 Explain What It Means for a Statistic to Be Resistant (1 of 6) EXAMPLE Computing a Median of a Data Set with an Even Number of Observations The following data represent the travel times (in minutes) to work for all seven employees of a start-up web development company. 23, 36, 23, 18, 5, 26, 43 Suppose a new employee is hired who has a 130 minute commute. How does this impact the value of the mean and median? Mean before new hire: 24. 9 minutes Median before new hire: 23 minutes Mean after new hire: 38 minutes Median after new hire: 24. 5 minutes Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

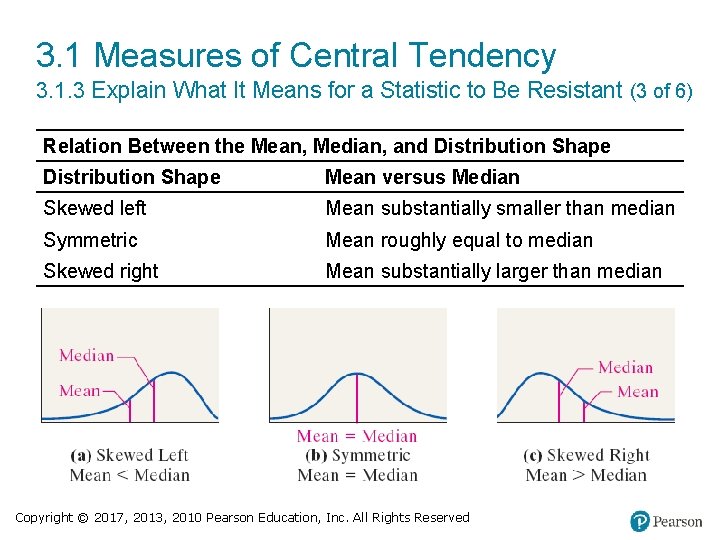
3. 1 Measures of Central Tendency 3. 1. 3 Explain What It Means for a Statistic to Be Resistant (2 of 6) A numerical summary of data is said to be resistant if extreme values (very large or small) relative to the data do not affect its value substantially. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 3 Explain What It Means for a Statistic to Be Resistant (3 of 6) Relation Between the Mean, Median, and Distribution Shape Mean versus Median Skewed left Mean substantially smaller than median Symmetric Mean roughly equal to median Skewed right Mean substantially larger than median Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

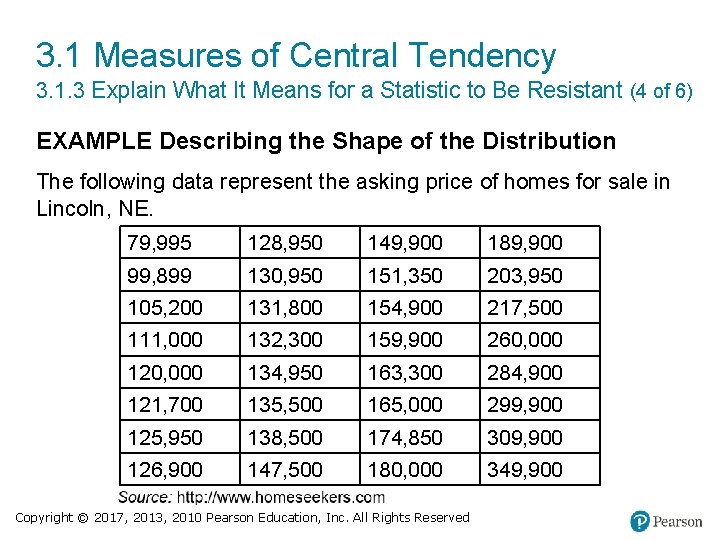
3. 1 Measures of Central Tendency 3. 1. 3 Explain What It Means for a Statistic to Be Resistant (4 of 6) EXAMPLE Describing the Shape of the Distribution The following data represent the asking price of homes for sale in Lincoln, NE. 79, 995 128, 950 149, 900 189, 900 99, 899 130, 950 151, 350 203, 950 105, 200 131, 800 154, 900 217, 500 111, 000 132, 300 159, 900 260, 000 120, 000 134, 950 163, 300 284, 900 121, 700 135, 500 165, 000 299, 900 125, 950 138, 500 174, 850 309, 900 126, 900 147, 500 180, 000 349, 900 Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

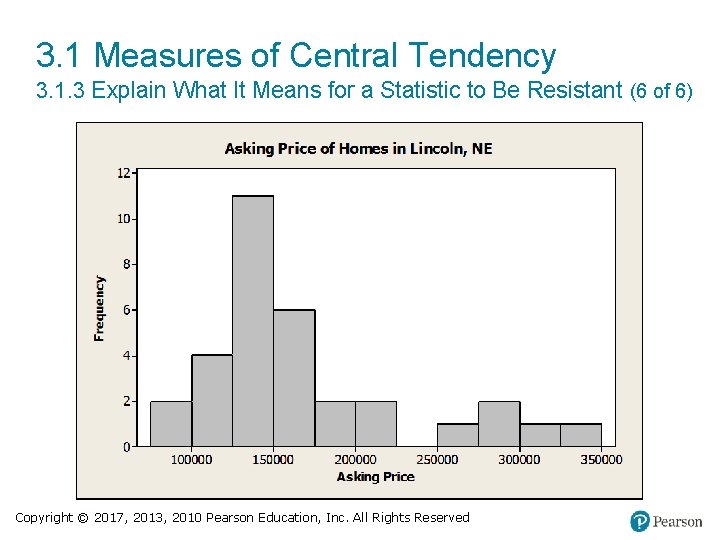
3. 1 Measures of Central Tendency 3. 1. 3 Explain What It Means for a Statistic to Be Resistant (5 of 6) Find the mean and median. Use the mean and median to identify the shape of the distribution. Verify your result by drawing a histogram of the data. The mean asking price is $168, 320 and the median asking price is $148, 700. Therefore, we would conjecture that the distribution is skewed right. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 3 Explain What It Means for a Statistic to Be Resistant (6 of 6) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 4 Determine the Mode of a Variable from Raw Data (1 of 7) The mode of a variable is the most frequent observation of the variable that occurs in the data set. A set of data can have no mode, one mode, or more than one mode. If no observation occurs more than once, we say the data have no mode. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

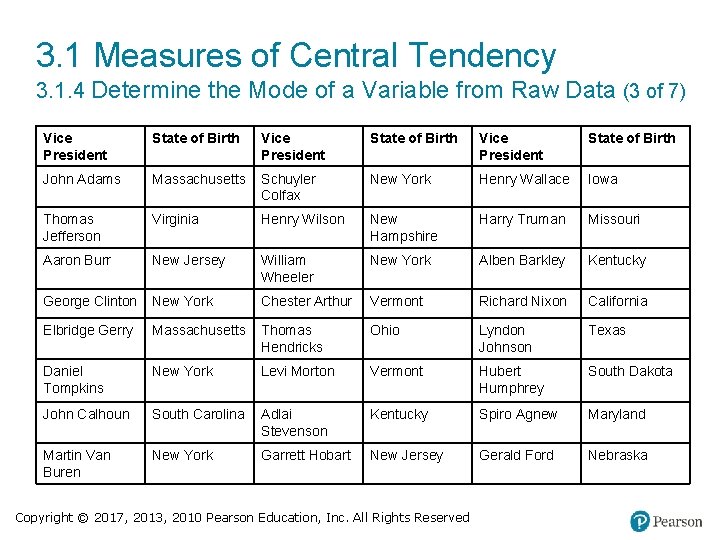
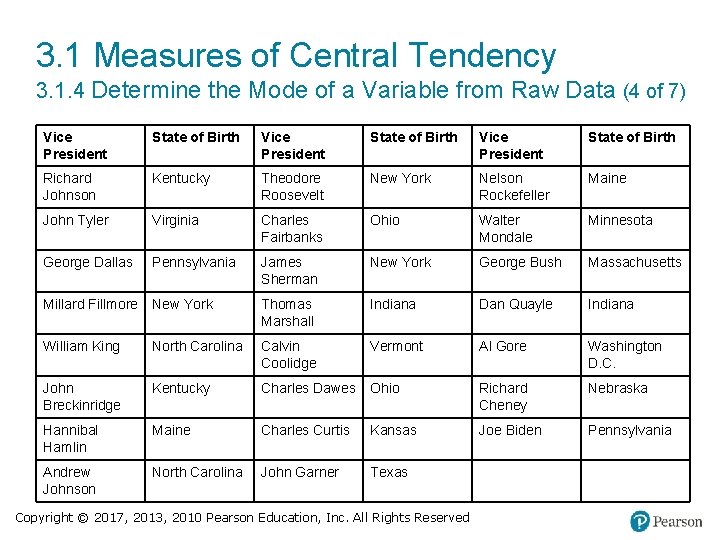
3. 1 Measures of Central Tendency 3. 1. 4 Determine the Mode of a Variable from Raw Data (2 of 7) EXAMPLE Finding the Mode of a Data Set The data on the next slide represent the Vice Presidents of the United States and their state of birth. Find the mode. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

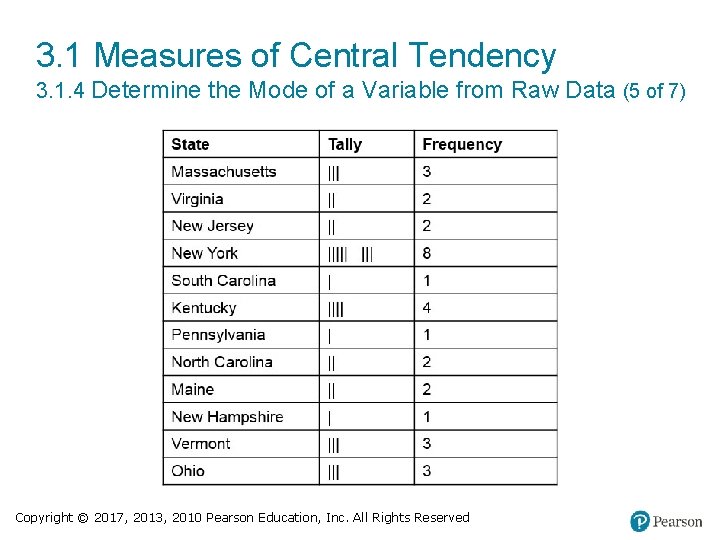
3. 1 Measures of Central Tendency 3. 1. 4 Determine the Mode of a Variable from Raw Data (3 of 7) Vice President State of Birth John Adams Massachusetts Schuyler Colfax New York Henry Wallace Iowa Thomas Jefferson Virginia Henry Wilson New Hampshire Harry Truman Missouri Aaron Burr New Jersey William Wheeler New York Alben Barkley Kentucky George Clinton New York Chester Arthur Vermont Richard Nixon California Elbridge Gerry Massachusetts Thomas Hendricks Ohio Lyndon Johnson Texas Daniel Tompkins New York Levi Morton Vermont Hubert Humphrey South Dakota John Calhoun South Carolina Adlai Stevenson Kentucky Spiro Agnew Maryland Martin Van Buren New York Garrett Hobart New Jersey Gerald Ford Nebraska Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 4 Determine the Mode of a Variable from Raw Data (4 of 7) Vice President State of Birth Richard Johnson Kentucky Theodore Roosevelt New York Nelson Rockefeller Maine John Tyler Virginia Charles Fairbanks Ohio Walter Mondale Minnesota George Dallas Pennsylvania James Sherman New York George Bush Massachusetts Millard Fillmore New York Thomas Marshall Indiana Dan Quayle Indiana William King North Carolina Calvin Coolidge Vermont Al Gore Washington D. C. John Breckinridge Kentucky Charles Dawes Ohio Richard Cheney Nebraska Hannibal Hamlin Maine Charles Curtis Kansas Joe Biden Pennsylvania Andrew Johnson North Carolina John Garner Texas blank Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 4 Determine the Mode of a Variable from Raw Data (5 of 7) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

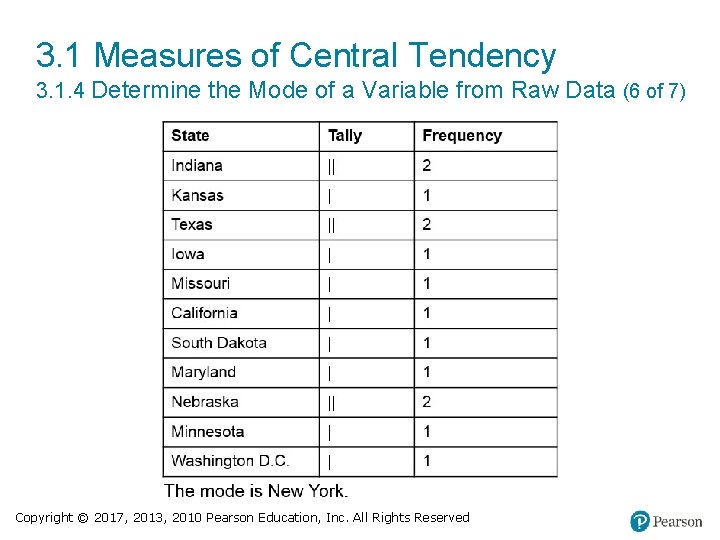
3. 1 Measures of Central Tendency 3. 1. 4 Determine the Mode of a Variable from Raw Data (6 of 7) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 1 Measures of Central Tendency 3. 1. 4 Determine the Mode of a Variable from Raw Data (7 of 7) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion Learning Objectives 1. Determine the range of a variable from raw data 2. Determine the standard deviation of a variable from raw data 3. Determine the variance of a variable from raw data 4. Use the Empirical Rule to describe data that are bell shaped 5. Use Chebyshev’s Inequality to describe any data set Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

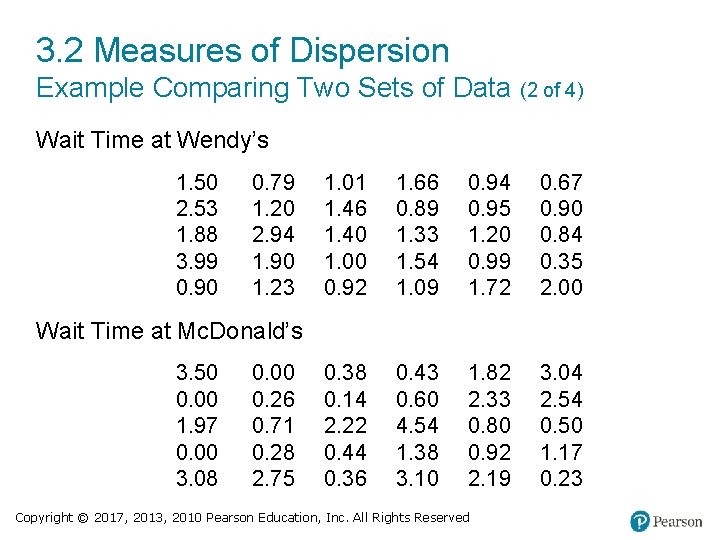
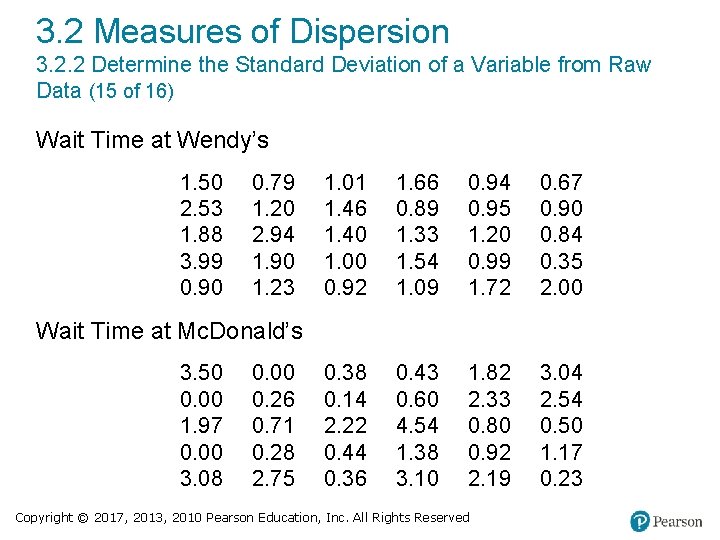
3. 2 Measures of Dispersion Example Comparing Two Sets of Data (1 of 4) To order food at a Mc. Donald’s restaurant, one must choose from multiple lines, while at Wendy’s Restaurant, one enters a single line. The following data represent the wait time (in minutes) in line for a simple random sample of 30 customers at each restaurant during the lunch hour. For each sample, answer the following: (a) What was the mean wait time? (b) Draw a histogram of each restaurant’s wait time. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion Example Comparing Two Sets of Data (2 of 4) Wait Time at Wendy’s 1. 50 2. 53 1. 88 3. 99 0. 90 0. 79 1. 20 2. 94 1. 90 1. 23 1. 01 1. 46 1. 40 1. 00 0. 92 1. 66 0. 89 1. 33 1. 54 1. 09 0. 94 0. 95 1. 20 0. 99 1. 72 0. 67 0. 90 0. 84 0. 35 2. 00 0. 38 0. 14 2. 22 0. 44 0. 36 0. 43 0. 60 4. 54 1. 38 3. 10 1. 82 2. 33 0. 80 0. 92 2. 19 3. 04 2. 54 0. 50 1. 17 0. 23 Wait Time at Mc. Donald’s 3. 50 0. 00 1. 97 0. 00 3. 08 0. 00 0. 26 0. 71 0. 28 2. 75 Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion Example Comparing Two Sets of Data (3 of 4) (a) The mean wait time in each line is 1. 39 minutes. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

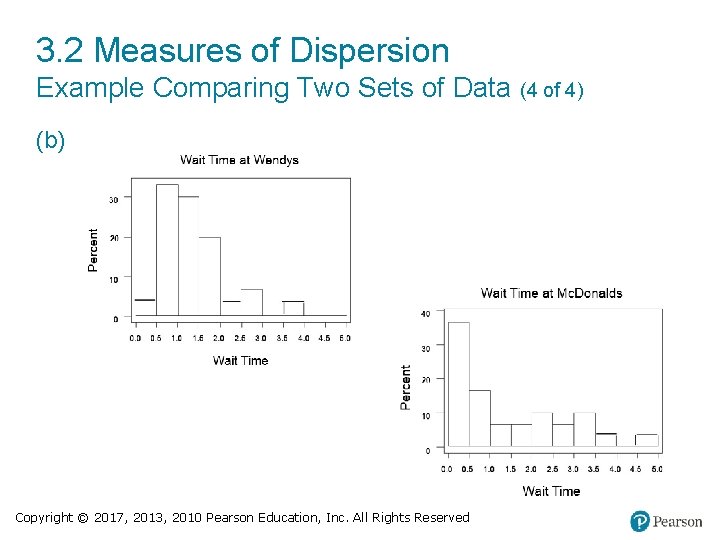
3. 2 Measures of Dispersion Example Comparing Two Sets of Data (4 of 4) (b) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 1 Determine the Range of a Variable from Raw Data (1 of 2) The range, R, of a variable is the difference between the largest data value and the smallest data values. That is, Range = R = Largest Data Value − Smallest Data Value Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 1 Determine the Range of a Variable from Raw Data (2 of 2) EXAMPLE Finding the Range of a Set of Data The following data represent the travel times (in minutes) to work for all seven employees of a start-up web development company. 23, 36, 23, 18, 5, 26, 43 Find the range. Range = 43 − 5 = 38 minutes Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (1 of 16) The population standard deviation of a variable is the square root of the sum of squared deviations about the population mean divided by the number of observations in the population, N. That is, it is the square root of the mean of the squared deviations about the population mean. The population standard deviation is symbolically represented by σ (lowercase Greek sigma). Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (2 of 16) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (3 of 16) A formula that is equivalent to the on the previous slide, called the computational formula, for determining the population standard deviation is Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

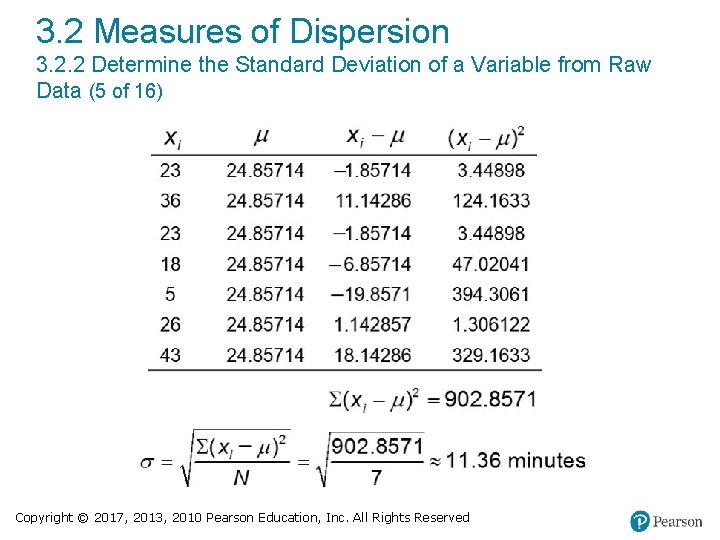
3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (4 of 16) EXAMPLE Computing a Population Standard Deviation The following data represent the travel times (in minutes) to work for all seven employees of a start-up web development company. 23, 36, 23, 18, 5, 26, 43 Compute the population standard deviation of this data. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (5 of 16) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (6 of 16) Using the computational formula, yields the same result. xi (xi )2 23 529 36 1296 23 529 18 324 5 25 26 676 43 1849 Σxi = 174 Σ(xi)2 = 5228 Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (7 of 16) The sample standard deviation, s, of a variable is the square root of the sum of squared deviations about the sample mean divided by n − 1, where n is the sample size. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (8 of 16) A formula that is equivalent to the on the previous slide, called the computational formula, for determining the sample standard deviation is Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (9 of 16) We call n − 1 the degrees of freedom because the first n − 1 observations have freedom to be whatever value they wish, but the nth value has no freedom. It must be whatever value forces the sum of the deviations about the mean to equal zero. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (10 of 16) EXAMPLE Computing a Sample Standard Deviation Here are the results of a random sample taken from the travel times (in minutes) to work for all seven employees of a start-up web development company: 5, 26, 36 Find the sample standard deviation. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (11 of 16) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (12 of 16) Using the computational formula, yields the same result. xi (xi )2 5 25 26 676 36 1296 Σxi = 67 Σ(xi)2 = 1997 Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (13 of 16) IN CLASS ACTIVITY The Sample Standard Deviation Using the pulse data from Section 3. 1, page 000, do the following: a) Obtain a simple random sample of n = 4 students and compute the sample standard deviation. b) Obtain a second simple random sample of n = 4 students and compute the sample standard deviation. c) Are the sample standard deviations the same? Why? Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (14 of 16) EXAMPLE Comparing Standard Deviations Determine the standard deviation waiting time for Wendy’s and Mc. Donald’s. Which is larger? Why? Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (15 of 16) Wait Time at Wendy’s 1. 50 2. 53 1. 88 3. 99 0. 90 0. 79 1. 20 2. 94 1. 90 1. 23 1. 01 1. 46 1. 40 1. 00 0. 92 1. 66 0. 89 1. 33 1. 54 1. 09 0. 94 0. 95 1. 20 0. 99 1. 72 0. 67 0. 90 0. 84 0. 35 2. 00 0. 38 0. 14 2. 22 0. 44 0. 36 0. 43 0. 60 4. 54 1. 38 3. 10 1. 82 2. 33 0. 80 0. 92 2. 19 3. 04 2. 54 0. 50 1. 17 0. 23 Wait Time at Mc. Donald’s 3. 50 0. 00 1. 97 0. 00 3. 08 0. 00 0. 26 0. 71 0. 28 2. 75 Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 2 Determine the Standard Deviation of a Variable from Raw Data (16 of 16) EXAMPLE Comparing Standard Deviations Sample standard deviation for Wendy’s: 0. 738 minutes Sample standard deviation for Mc. Donald’s: 1. 265 minutes Recall from earlier that the data is more dispersed for Mc. Donald’s resulting in a larger standard deviation. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 3 Determine the Variance of a Variable from Raw Data (1 of 3) The variance of a variable is the square of the standard deviation. The population variance is σ2 and the sample variance is s 2. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 3 Determine the Variance of a Variable from Raw Data (2 of 3) EXAMPLE Computing a Population Variance The following data represent the travel times (in minutes) to work for all seven employees of a start-up web development company. 23, 36, 23, 18, 5, 26, 43 Compute the population and sample variance of this data. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 3 Determine the Variance of a Variable from Raw Data (3 of 3) EXAMPLE Computing a Population Variance Recall that the population standard deviation (from slide #49) is σ = 11. 36 so the population variance is σ2 = 129. 05 minutes and that the sample standard deviation (from slide #55) is s = 15. 82, so the sample variance is s 2 = 250. 27 minutes Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

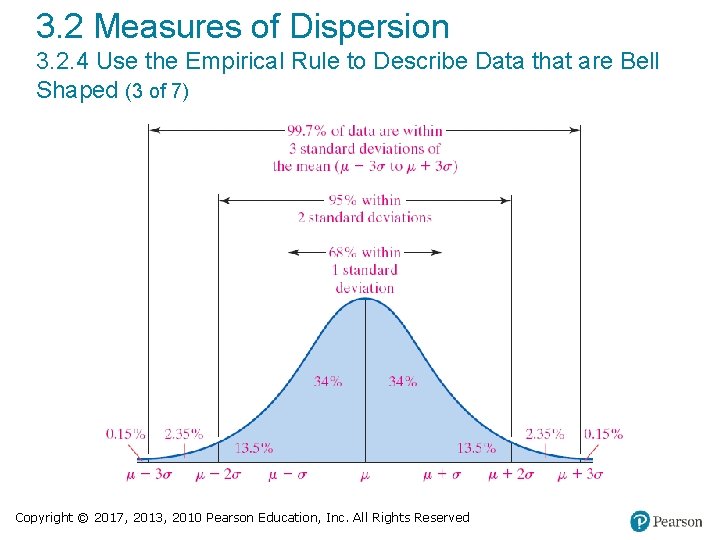
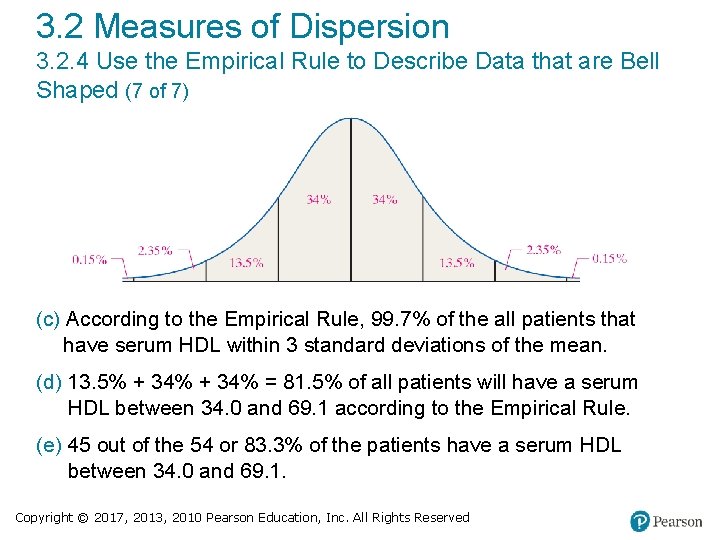
3. 2 Measures of Dispersion 3. 2. 4 Use the Empirical Rule to Describe Data that are Bell Shaped (1 of 7) The Empirical Rule If a distribution is roughly bell shaped, then • Approximately 68% of the data will lie within 1 standard deviation of the mean. That is, approximately 68% of the data lie between μ − 1σ and μ + 1σ. • Approximately 95% of the data will lie within 2 standard deviations of the mean. That is, approximately 95% of the data lie between μ − 2σ and μ + 2σ. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 4 Use the Empirical Rule to Describe Data that are Bell Shaped (2 of 7) The Empirical Rule If a distribution is roughly bell shaped, then • Approximately 99. 7% of the data will lie within 3 standard deviations of the mean. That is, approximately 99. 7% of the data lie between μ − 3σ and μ + 3σ. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 4 Use the Empirical Rule to Describe Data that are Bell Shaped (3 of 7) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

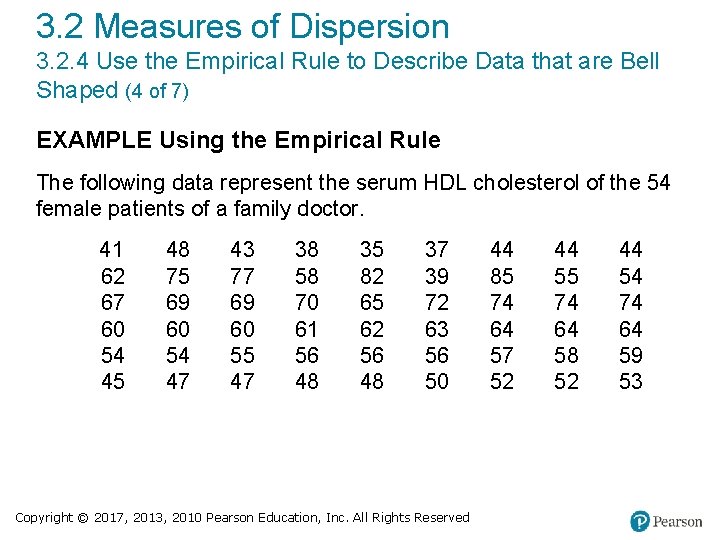
3. 2 Measures of Dispersion 3. 2. 4 Use the Empirical Rule to Describe Data that are Bell Shaped (4 of 7) EXAMPLE Using the Empirical Rule The following data represent the serum HDL cholesterol of the 54 female patients of a family doctor. 41 62 67 60 54 45 48 75 69 60 54 47 43 77 69 60 55 47 38 58 70 61 56 48 35 82 65 62 56 48 37 39 72 63 56 50 Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved 44 85 74 64 57 52 44 55 74 64 58 52 44 54 74 64 59 53

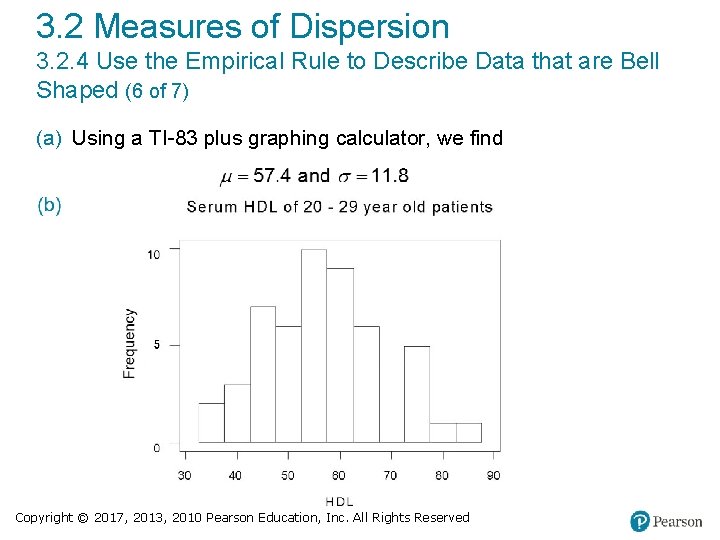
3. 2 Measures of Dispersion 3. 2. 4 Use the Empirical Rule to Describe Data that are Bell Shaped (5 of 7) a) Compute the population mean and standard deviation. b) Draw a histogram to verify the data is bell-shaped. c) Determine the percentage of all patients that have serum HDL within 3 standard deviations of the mean according to the Empirical Rule. d) Determine the percentage of all patients that have serum HDL between 34 and 69. 1 according to the Empirical Rule. e) Determine the actual percentage of patients that have serum HDL between 34 and 69. 1. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 4 Use the Empirical Rule to Describe Data that are Bell Shaped (6 of 7) (a) Using a TI-83 plus graphing calculator, we find Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 4 Use the Empirical Rule to Describe Data that are Bell Shaped (7 of 7) (c) According to the Empirical Rule, 99. 7% of the all patients that have serum HDL within 3 standard deviations of the mean. (d) 13. 5% + 34% = 81. 5% of all patients will have a serum HDL between 34. 0 and 69. 1 according to the Empirical Rule. (e) 45 out of the 54 or 83. 3% of the patients have a serum HDL between 34. 0 and 69. 1. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 2 Measures of Dispersion 3. 2. 5 Use Chebyshev’s Inequality to Describe Any Set of Data (1 of 2) Note: We can also use Chebyshev’s Inequality based on sample data. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

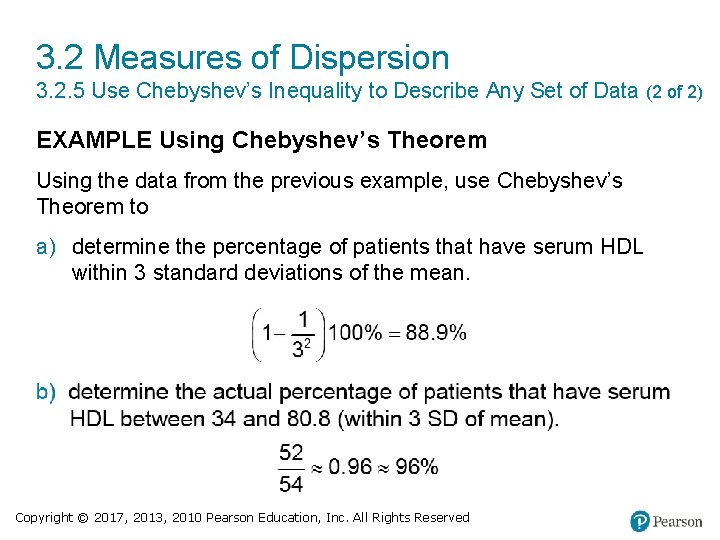
3. 2 Measures of Dispersion 3. 2. 5 Use Chebyshev’s Inequality to Describe Any Set of Data (2 of 2) EXAMPLE Using Chebyshev’s Theorem Using the data from the previous example, use Chebyshev’s Theorem to a) determine the percentage of patients that have serum HDL within 3 standard deviations of the mean. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 3 Measures of Central Tendency and Dispersion from Grouped Data Learning Objectives 1. Approximate the mean of a variable from grouped data 2. Compute the weighted mean 3. Approximate the standard deviation of a variable from grouped data Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 3 Measures of Central Tendency and Dispersion from Grouped Data 3. 3. 1 Approximate the Mean of a Variable from Grouped Data (1 of 4) We have discussed how to compute descriptive statistics from raw data, but often the only available data have already been summarized in frequency distributions (grouped data). Although we cannot find exact values of the mean or standard deviation without raw data, we can approximate these measures using the techniques discussed in this section. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 3 Measures of Central Tendency and Dispersion from Grouped Data 3. 3. 1 Approximate the Mean of a Variable from Grouped Data (2 of 4) Approximate the Mean of a Variable from a Frequency Distribution Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

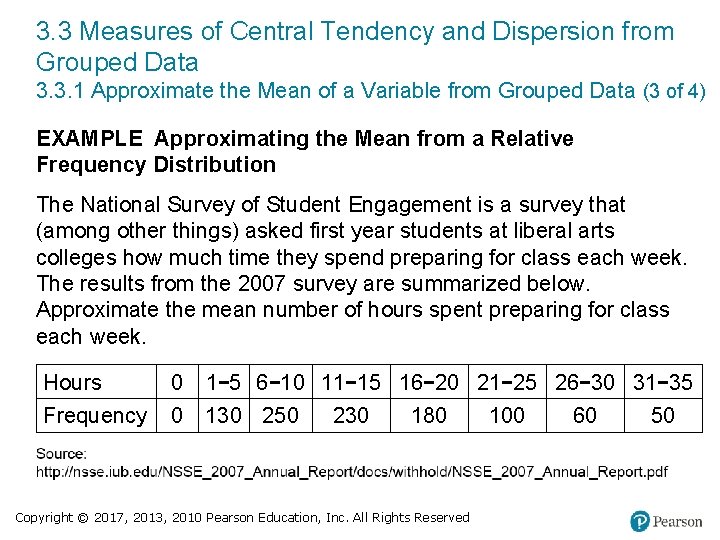
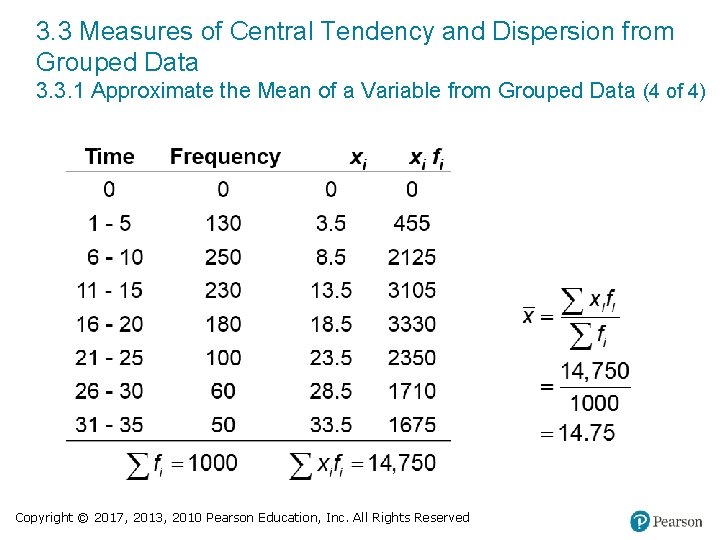
3. 3 Measures of Central Tendency and Dispersion from Grouped Data 3. 3. 1 Approximate the Mean of a Variable from Grouped Data (3 of 4) EXAMPLE Approximating the Mean from a Relative Frequency Distribution The National Survey of Student Engagement is a survey that (among other things) asked first year students at liberal arts colleges how much time they spend preparing for class each week. The results from the 2007 survey are summarized below. Approximate the mean number of hours spent preparing for class each week. Hours 0 1− 5 6− 10 11− 15 16− 20 21− 25 26− 30 31− 35 Frequency 0 130 250 230 180 Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved 100 60 50

3. 3 Measures of Central Tendency and Dispersion from Grouped Data 3. 3. 1 Approximate the Mean of a Variable from Grouped Data (4 of 4) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 3 Measures of Central Tendency and Dispersion from Grouped Data 3. 3. 2 Compute the Weighted Mean (1 of 2) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 3 Measures of Central Tendency and Dispersion from Grouped Data 3. 3. 2 Compute the Weighted Mean (2 of 2) EXAMPLE Computed a Weighted Mean Bob goes to the “Buy the Weigh” Nut store and creates his own bridge mix. He combines 1 pound of raisins, 2 pounds of chocolate covered peanuts, and 1. 5 pounds of cashews. The raisins cost $1. 25 per pound, the chocolate covered peanuts cost $3. 25 per pound, and the cashews cost $5. 40 per pound. What is the cost per pound of this mix? Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 3 Measures of Central Tendency and Dispersion from Grouped Data 3. 3. 3 Approximate the Standard Deviation of a Variable from Grouped Data (1 of 4) Approximate the Standard Deviation of a Variable from a Frequency Distribution Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 3 Measures of Central Tendency and Dispersion from Grouped Data 3. 3. 3 Approximate the Standard Deviation of a Variable from Grouped Data (2 of 4) An algebraically equivalent formula for the population standard deviation is Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

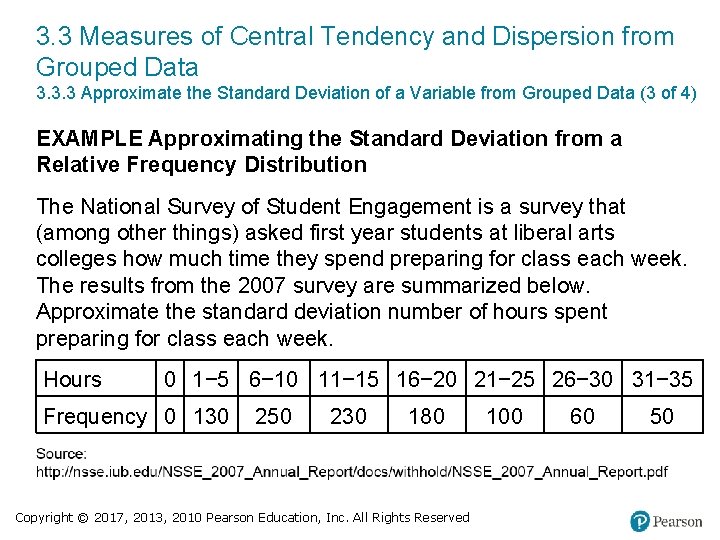
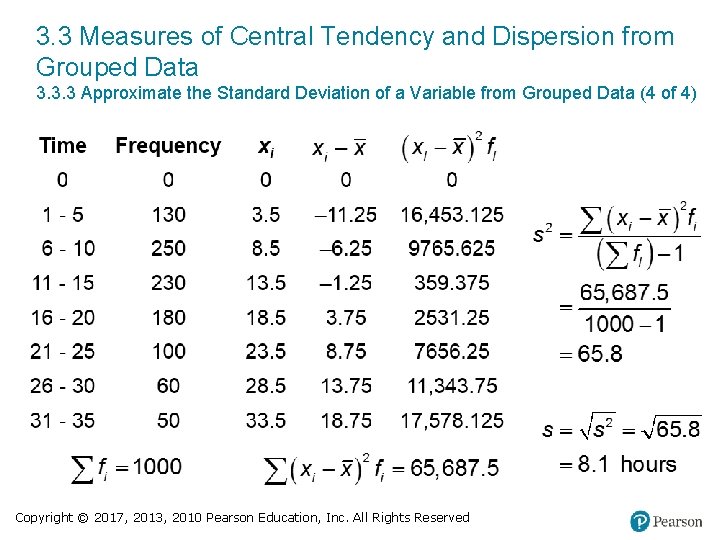
3. 3 Measures of Central Tendency and Dispersion from Grouped Data 3. 3. 3 Approximate the Standard Deviation of a Variable from Grouped Data (3 of 4) EXAMPLE Approximating the Standard Deviation from a Relative Frequency Distribution The National Survey of Student Engagement is a survey that (among other things) asked first year students at liberal arts colleges how much time they spend preparing for class each week. The results from the 2007 survey are summarized below. Approximate the standard deviation number of hours spent preparing for class each week. Hours 0 1− 5 6− 10 11− 15 16− 20 21− 25 26− 30 31− 35 Frequency 0 130 250 230 180 Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved 100 60 50

3. 3 Measures of Central Tendency and Dispersion from Grouped Data 3. 3. 3 Approximate the Standard Deviation of a Variable from Grouped Data (4 of 4) Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers Learning Objectives 1. Determine and interpret z-scores 2. Interpret percentiles 3. Determine and interpret quartiles 4. Determine and interpret the interquartile range 5. Check a set of data for outliers Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 1 Determine and Interpret z-Scores (1 of 3) The z-score represents the distance that a data value is from the mean in terms of the number of standard deviations. We find it by subtracting the mean from the data value and dividing this result by the standard deviation. There is both a population z-score and a sample z-score: Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 1 Determine and Interpret z-Scores (2 of 3) EXAMPLE Using Z-Scores The mean height of males 20 years or older is 69. 1 inches with a standard deviation of 2. 8 inches. The mean height of females 20 years or older is 63. 7 inches with a standard deviation of 2. 7 inches. Data is based on information obtained from National Health and Examination Survey. Who is relatively taller? Kevin Garnett whose height is 83 inches or Candace Parker whose height is 76 inches Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 1 Determine and Interpret z-Scores (3 of 3) Kevin Garnett’s height is 4. 96 standard deviations above the mean. Candace Parker’s height is 4. 56 standard deviations above the mean. Kevin Garnett is relatively taller. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 2 Interpret Percentiles (1 of 3) The kth percentile, denoted, Pk , of a set of data is a value such that k percent of the observations are less than or equal to the value. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 2 Interpret Percentiles (2 of 3) EXAMPLE Interpret a Percentile The Graduate Record Examination (GRE) is a test required for admission to many U. S. graduate schools. The University of Pittsburgh Graduate School of Public Health requires a GRE score no less than the 70 th percentile for admission into their Human Genetics MPH or MS program. (Source: http: //www. publichealth. pitt. edu/interior. php? page. ID=101. ) Interpret this admissions requirement. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 2 Interpret Percentiles (3 of 3) EXAMPLE Interpret a Percentile In general, the 70 th percentile is the score such that 70% of the individuals who took the exam scored worse, and 30% of the individuals scores better. In order to be admitted to this program, an applicant must score as high or higher than 70% of the people who take the GRE. Put another way, the individual’s score must be in the top 30%. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

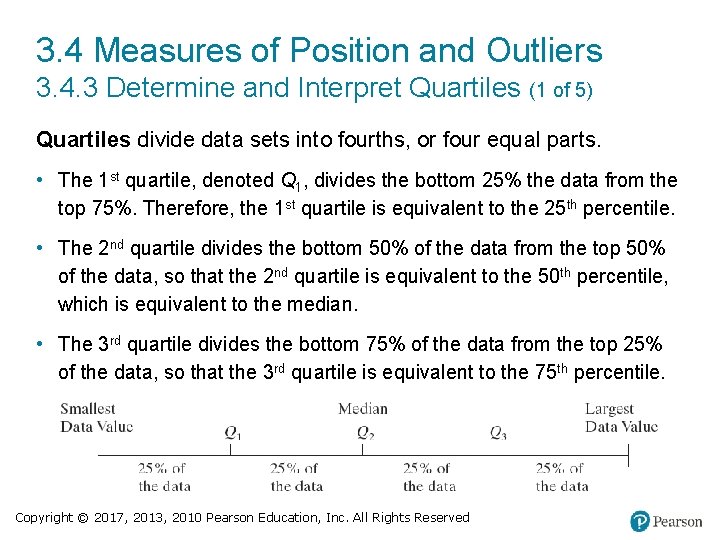
3. 4 Measures of Position and Outliers 3. 4. 3 Determine and Interpret Quartiles (1 of 5) Quartiles divide data sets into fourths, or four equal parts. • The 1 st quartile, denoted Q 1, divides the bottom 25% the data from the top 75%. Therefore, the 1 st quartile is equivalent to the 25 th percentile. • The 2 nd quartile divides the bottom 50% of the data from the top 50% of the data, so that the 2 nd quartile is equivalent to the 50 th percentile, which is equivalent to the median. • The 3 rd quartile divides the bottom 75% of the data from the top 25% of the data, so that the 3 rd quartile is equivalent to the 75 th percentile. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 3 Determine and Interpret Quartiles (2 of 5) Finding Quartiles Step 1: Arrange the data in ascending order. Step 2: Determine the median, M, or second quartile, Q 2. Step 3: Divide the data set into halves: the observations below (to the left of) M and the observations above M. The first quartile, Q 1, is the median of the bottom half, and the third quartile, Q 3, is the median of the top half. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 3 Determine and Interpret Quartiles (3 of 5) EXAMPLE Finding and Interpreting Quartiles A group of Brigham Young University—Idaho students (Matthew Herring, Nathan Spencer, Mark Walker, and Mark Steiner) collected data on the speed of vehicles traveling through a construction zone on a state highway, where the posted speed was 25 mph. The recorded speed of 14 randomly selected vehicles is given below: 20, 24, 27, 28, 29, 30, 32, 33, 34, 36, 38, 39, 40 Find and interpret the quartiles for speed in the construction zone. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 3 Determine and Interpret Quartiles (4 of 5) EXAMPLE Finding and Interpreting Quartiles Step 1: The data is already in ascending order. Step 2: There are n = 14 observations, so the median, or second quartile, Q 2, is the mean of the 7 th and 8 th observations. Therefore, M = 32. 5. Step 3: The median of the bottom half of the data is the first quartile, Q 1. 20, 24, 27, 28, 29, 30, 32 The median of these seven observations is 28. Therefore, Q 1 = 28. The median of the top half of the data is the third quartile, Q 3. Therefore, Q 3 = 38. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 3 Determine and Interpret Quartiles (5 of 5) Interpretation: • 25% of the speeds are less than or equal to the first quartile, 28 miles per hour, and 75% of the speeds are greater than 28 miles per hour. • 50% of the speeds are less than or equal to the second quartile, 32. 5 miles per hour, and 50% of the speeds are greater than 32. 5 miles per hour. • 75% of the speeds are less than or equal to the third quartile, 38 miles per hour, and 25% of the speeds are greater than 38 miles per hour. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 4 Determine and Interpret the Interquartile Range (1 of 3) The interquartile range, IQR, is the range of the middle 50% of the observations in a data set. That is, the IQR is the difference between the third and first quartiles and is found using the formula IQR = Q 3 − Q 1 Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 4 Determine and Interpret the Interquartile Range (2 of 3) EXAMPLE Determining and Interpreting the Interquartile Range Determine and interpret the interquartile range of the speed data. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

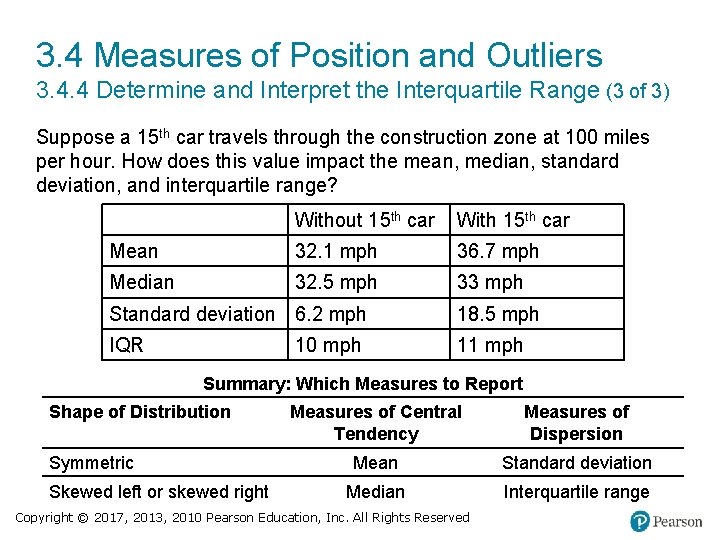
3. 4 Measures of Position and Outliers 3. 4. 4 Determine and Interpret the Interquartile Range (3 of 3) Suppose a 15 th car travels through the construction zone at 100 miles per hour. How does this value impact the mean, median, standard deviation, and interquartile range? blank Without 15 th car With 15 th car Mean 32. 1 mph 36. 7 mph Median 32. 5 mph 33 mph Standard deviation 6. 2 mph 18. 5 mph IQR 11 mph 10 mph Summary: Which Measures to Report Shape of Distribution Symmetric Skewed left or skewed right Measures of Central Tendency Measures of Dispersion Mean Standard deviation Median Interquartile range Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 5 Check a Set of Data for Outliers (1 of 2) Checking for Outliers by Using Quartiles Step 1 Determine the first and third quartiles of the data. Step 2 Compute the interquartile range. Step 3 Determine the fences. Fences serve as cutoff points for determining outliers. Lower Fence = Q 1 − 1. 5(IQR) Upper Fence = Q 3 + 1. 5(IQR) Step 4 If a data value is less than the lower fence or greater than the upper fence, it is considered an outlier. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 4 Measures of Position and Outliers 3. 4. 5 Check a Set of Data for Outliers (2 of 2) EXAMPLE Determining and Interpreting the Interquartile Range Check the speed data for outliers. Step 1: The first and third quartiles are Q 1 = 28 mph and Q 3 = 38 mph. Step 2: The interquartile range is 10 mph. Step 3: The fences are Lower Fence = Q 1 − 1. 5(IQR) = 28 − 1. 5(10) = 13 mph Upper Fence = Q 3 + 1. 5(IQR) = 38 + 1. 5(10) = 53 mph Step 4: There are no values less than 13 mph or greater than 53 mph. Therefore, there are no outliers. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 5 The Five-Number Summary and Boxplots Learning Objectives 1. Compute the five-number summary 2. Draw and interpret boxplots Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 5 The Five-Number Summary and Boxplots 3. 5. 1 Compute the Five-Number Summary (1 of 4) The five-number summary of a set of data consists of the smallest data value, Q 1, the median, Q 3, and the largest data value. We organize the five-number summary as follows: Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 5 The Five-Number Summary and Boxplots 3. 5. 1 Compute the Five-Number Summary (2 of 4) EXAMPLE Obtaining the Five-Number Summary Every six months, the United States Federal Reserve Board conducts a survey of credit card plans in the U. S. The following data are the interest rates charged by 10 credit card issuers randomly selected for the July 2005 survey. Determine the fivenumber summary of the data. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 5 The Five-Number Summary and Boxplots 3. 5. 1 Compute the Five-Number Summary (3 of 4) EXAMPLE Obtaining the Five-Number Summary Institution Pulaski Bank and Trust Company Rate 6. 5% Rainier Pacific Savings Bank 12. 0% Wells Fargo Bank NA 14. 4% Firstbank of Colorado 14. 4% Lafayette Ambassador Bank 14. 3% Infibank 13. 0% United Bank, Inc. 13. 3% First National Bank of The Mid-Cities 13. 9% Bank of Louisiana Bar Harbor Bank and Trust Company Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved 9. 9% 14. 5%

3. 5 The Five-Number Summary and Boxplots 3. 5. 1 Compute the Five-Number Summary (4 of 4) EXAMPLE Obtaining the Five-Number Summary First, we write the data in ascending order: 6. 5%, 9. 9%, 12. 0%, 13. 3%, 13. 9%, 14. 3%, 14. 4%, 14. 5% The smallest number is 6. 5%. The largest number is 14. 5%. The first quartile is 12. 0%. The second quartile is 13. 6%. The third quartile is 14. 4%. Five-number Summary: 6. 5% 12. 0% 13. 6% 14. 4% Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved 14. 5%

3. 5 The Five-Number Summary and Boxplots 3. 5. 2 Draw and Interpret Boxplots (1 of 6) Drawing a Boxplot Step 1 Determine the lower and upper fences. Lower Fence = Q 1 − 1. 5(IQR) Upper Fence = Q 3 + 1. 5(IQR) where IQR = Q 3 − Q 1 Step 2 Draw a number line long enough to include the maximum and minimum values. Insert vertical lines at Q 1, M, and Q 3. Enclose these vertical lines in a box. Step 3 Label the lower and upper fences. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 5 The Five-Number Summary and Boxplots 3. 5. 2 Draw and Interpret Boxplots (2 of 6) Drawing a Boxplot Step 4 Draw a line from Q 1 to the smallest data value that is larger than the lower fence. Draw a line from Q 3 to the largest data value that is smaller than the upper fence. These lines are called whiskers. Step 5 Any data values less than the lower fence or greater than the upper fence are outliers and are marked with an asterisk (*). Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 5 The Five-Number Summary and Boxplots 3. 5. 2 Draw and Interpret Boxplots (3 of 6) EXAMPLE Constructing a Boxplot Every six months, the United States Federal Reserve Board conducts a survey of credit card plans in the U. S. The following data are the interest rates charged by 10 credit card issuers randomly selected for the July 2005 survey. Construct a boxplot of the data. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

3. 5 The Five-Number Summary and Boxplots 3. 5. 2 Draw and Interpret Boxplots (4 of 6) EXAMPLE Constructing a Boxplot Institution Pulaski Bank and Trust Company Rate 6. 5% Rainier Pacific Savings Bank 12. 0% Wells Fargo Bank NA 14. 4% Firstbank of Colorado 14. 4% Lafayette Ambassador Bank 14. 3% Infibank 13. 0% United Bank, Inc. 13. 3% First National Bank of The Mid-Cities 13. 9% Bank of Louisiana Bar Harbor Bank and Trust Company Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved 9. 9% 14. 5%

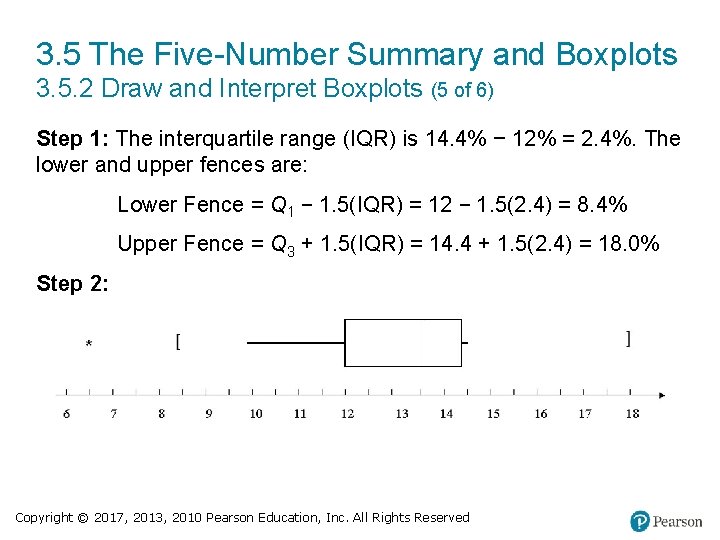
3. 5 The Five-Number Summary and Boxplots 3. 5. 2 Draw and Interpret Boxplots (5 of 6) Step 1: The interquartile range (IQR) is 14. 4% − 12% = 2. 4%. The lower and upper fences are: Lower Fence = Q 1 − 1. 5(IQR) = 12 − 1. 5(2. 4) = 8. 4% Upper Fence = Q 3 + 1. 5(IQR) = 14. 4 + 1. 5(2. 4) = 18. 0% Step 2: Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved

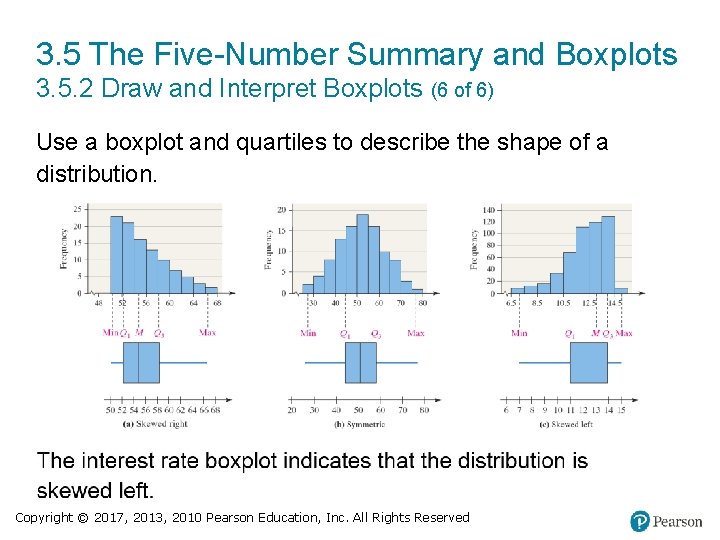
3. 5 The Five-Number Summary and Boxplots 3. 5. 2 Draw and Interpret Boxplots (6 of 6) Use a boxplot and quartiles to describe the shape of a distribution. Copyright © 2017, 2013, 2010 Pearson Education, Inc. All Rights Reserved
 Statistics informed decisions using data 5th edition pdf
Statistics informed decisions using data 5th edition pdf Poster making meaning
Poster making meaning Mis chapter 6
Mis chapter 6 Mis
Mis Principles of marketing fifth european edition
Principles of marketing fifth european edition Lazarus theory
Lazarus theory Fundamentals of corporate finance fifth edition
Fundamentals of corporate finance fifth edition Fifth edition chemistry a molecular approach
Fifth edition chemistry a molecular approach Segregat
Segregat Molecular biology
Molecular biology Human anatomy fifth edition
Human anatomy fifth edition Human anatomy fifth edition
Human anatomy fifth edition Screening decisions and preference decisions
Screening decisions and preference decisions Statistics: unlocking the power of data 1st edition
Statistics: unlocking the power of data 1st edition Elementary statistics 13th edition chapter 1
Elementary statistics 13th edition chapter 1 Decision tree in supply chain management
Decision tree in supply chain management Making spatial decisions using gis
Making spatial decisions using gis Elementary statistics 13th edition answers
Elementary statistics 13th edition answers Picturing distributions with graphs
Picturing distributions with graphs P value
P value Elementary statistics picturing the world 6th edition
Elementary statistics picturing the world 6th edition Elementary statistics tenth edition
Elementary statistics tenth edition Elementary statistics picturing the world 6th edition
Elementary statistics picturing the world 6th edition Basic business statistics 12th edition
Basic business statistics 12th edition Elementary statistics 13th edition
Elementary statistics 13th edition Joey's first 14 quiz grades in a marking period were
Joey's first 14 quiz grades in a marking period were Introduction to statistics what is statistics
Introduction to statistics what is statistics Senge fifth discipline summary
Senge fifth discipline summary Fifth chapter menu
Fifth chapter menu Using financial accounting information 10th edition
Using financial accounting information 10th edition Statistics for managers using ms excel solutions
Statistics for managers using ms excel solutions Chapter 4 financial decisions and planning
Chapter 4 financial decisions and planning Chapter 4 financial decisions and planning
Chapter 4 financial decisions and planning Designing a buying plan
Designing a buying plan Chapter 7 buying decisions
Chapter 7 buying decisions Chapter 10 personal loans and purchasing decisions
Chapter 10 personal loans and purchasing decisions Chapter 1 economic decisions and systems answer key
Chapter 1 economic decisions and systems answer key Chapter 10 making capital investment decisions
Chapter 10 making capital investment decisions Chapter 4 financial decisions and planning
Chapter 4 financial decisions and planning Chapter 4 financial decisions and planning
Chapter 4 financial decisions and planning Chapter 4 financial decisions and planning
Chapter 4 financial decisions and planning Nwc change
Nwc change Informed action meaning
Informed action meaning 4 r's trauma informed care
4 r's trauma informed care Lgbt trauma informed care
Lgbt trauma informed care Anita ravi md
Anita ravi md Pillars of trauma informed care
Pillars of trauma informed care Keep satisfied manage closely monitor keep informed
Keep satisfied manage closely monitor keep informed Psychologically informed environment
Psychologically informed environment What is threat matrix
What is threat matrix Trauma-informed care activities for staff
Trauma-informed care activities for staff Free prior and informed consent
Free prior and informed consent Informed (heuristic) search strategies
Informed (heuristic) search strategies Trauma informed workplace
Trauma informed workplace An informed guess or assumption about a certain problem
An informed guess or assumption about a certain problem Informed and uninformed search
Informed and uninformed search You should seek to be an informed user of it because
You should seek to be an informed user of it because Trauma-informed questions for clients
Trauma-informed questions for clients 4 r's trauma informed care
4 r's trauma informed care Jennifer masi
Jennifer masi Kobtion
Kobtion Libby bergman
Libby bergman Tina champagne sensory modulation
Tina champagne sensory modulation Psychologically informed environments
Psychologically informed environments Psychologically informed environments
Psychologically informed environments Dasar hukum informed consent adalah
Dasar hukum informed consent adalah Informed search example
Informed search example Best first search
Best first search Usps informed consent
Usps informed consent Informed delivery for business mailers
Informed delivery for business mailers Ethical principles governing informed consent process
Ethical principles governing informed consent process Uninformed search is also called as
Uninformed search is also called as Trauma informed advising
Trauma informed advising Informed personal response
Informed personal response Psychologically informed environment
Psychologically informed environment Acessexual
Acessexual What philosophical ideas informed the founding generation?
What philosophical ideas informed the founding generation? Informed delivery campaigns
Informed delivery campaigns Advantages of informed consent
Advantages of informed consent Informed user of information systems
Informed user of information systems Trauma informed practice
Trauma informed practice Decision making skills
Decision making skills Examples of informed search
Examples of informed search Trauma infromed
Trauma infromed 8 puzzle python
8 puzzle python Trauma-informed care cheat sheet
Trauma-informed care cheat sheet Slbet portugal
Slbet portugal Broad informed consent
Broad informed consent Informed search
Informed search Trauma informed practice
Trauma informed practice Informed consent brochure
Informed consent brochure Trauma informed care for foster youth
Trauma informed care for foster youth Informed and uninformed search
Informed and uninformed search Essential elements of informed consent
Essential elements of informed consent First korotkoff sound
First korotkoff sound Fifth gear loop the loop
Fifth gear loop the loop Ffa creed fifth paragraph
Ffa creed fifth paragraph Soliloquy 5 hamlet
Soliloquy 5 hamlet Fifth standard solar
Fifth standard solar Hercules fifth labor
Hercules fifth labor Fifth business archetypes
Fifth business archetypes Ffa jeopardy
Ffa jeopardy Fifth third bank hsa
Fifth third bank hsa Compensating fifth wheel
Compensating fifth wheel