SPECIALIST MATHS Differential Equations Week 1 Differential Equations



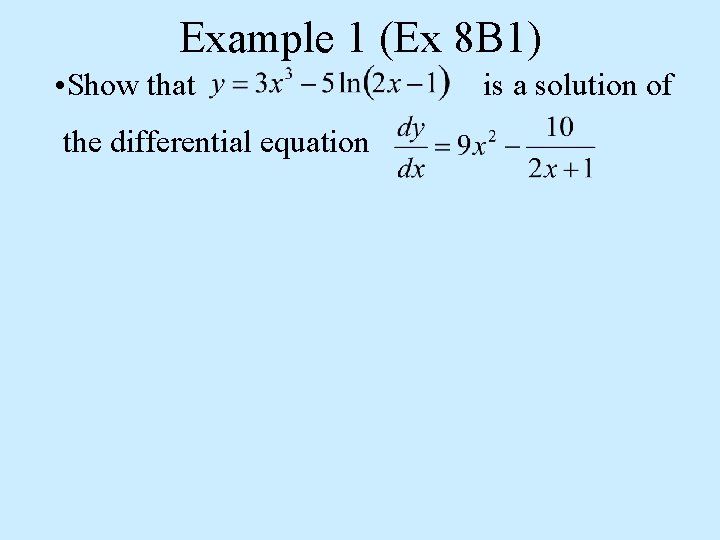



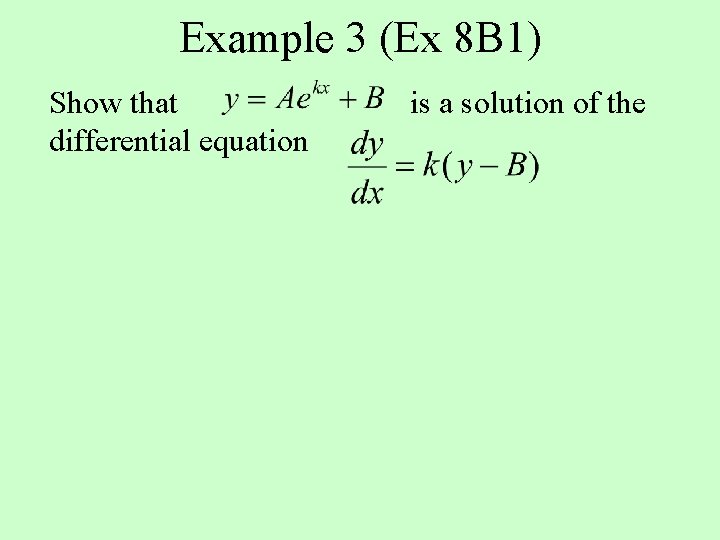




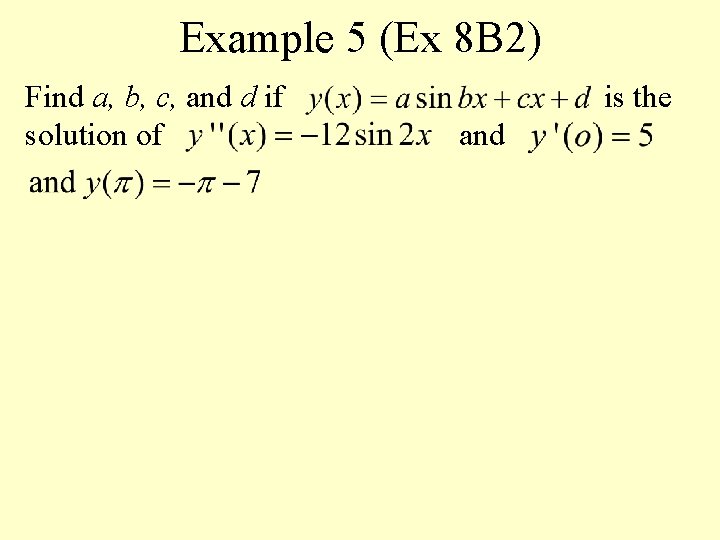

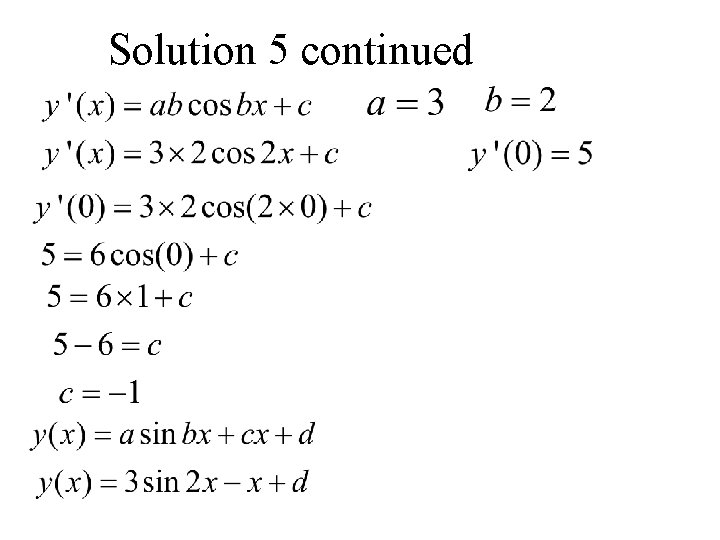






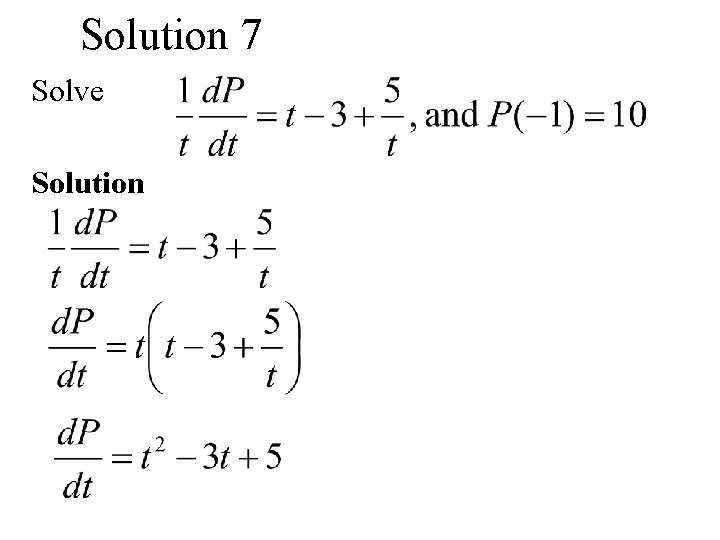
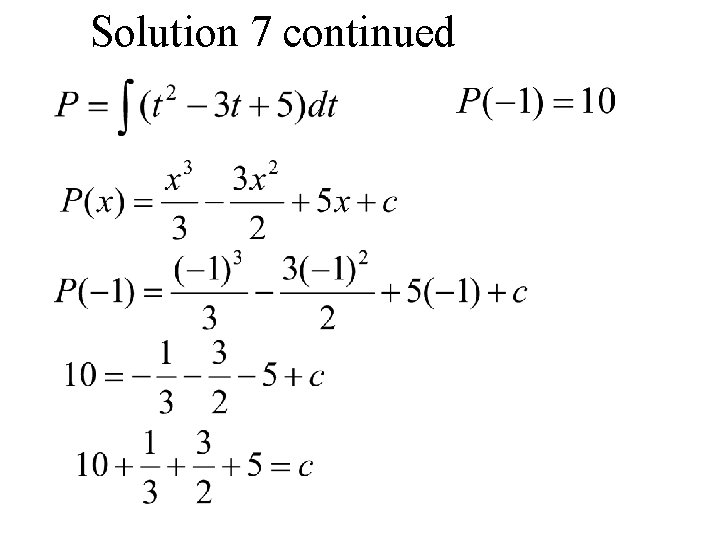






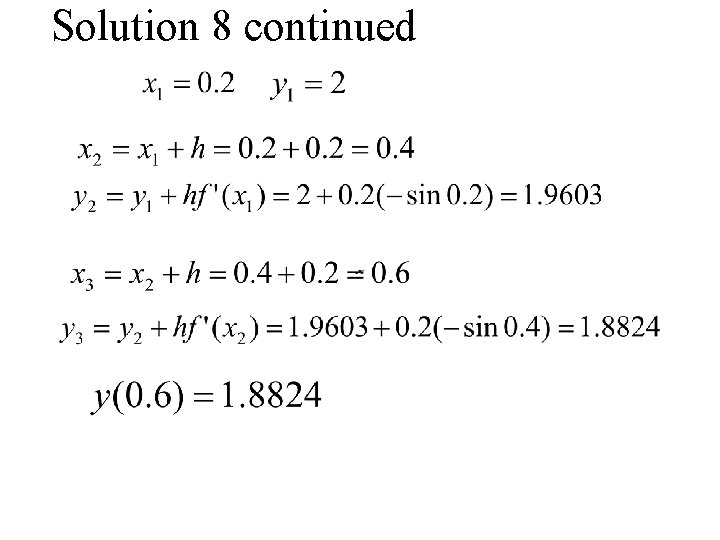


- Slides: 33

SPECIALIST MATHS Differential Equations Week 1

Differential Equations • The solution to a differential equations is a function that obeys it. • Types of equations we will study are of the form:

Obtaining Differential Equations • To obtain a differential equation from a function, we must: • differentiate the function, then • manipulate the result to achieve the appropriate equation.
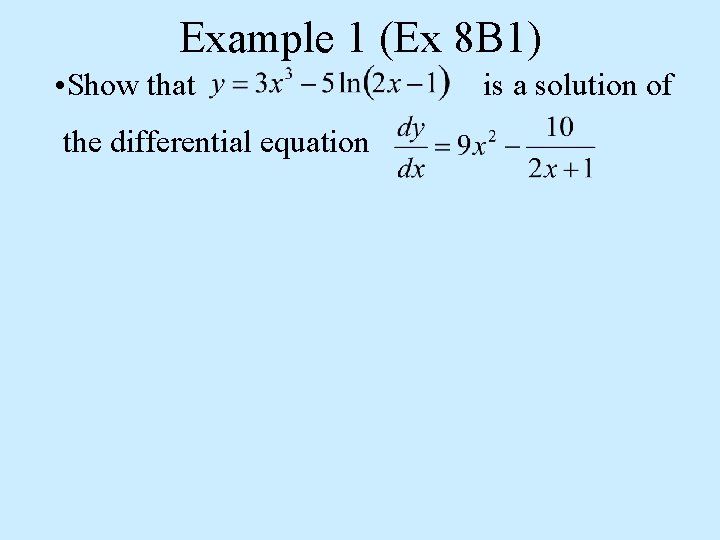
Example 1 (Ex 8 B 1) • Show that the differential equation is a solution of

Solution 1 • Show that e differential equation is a solution of th

Example 2 (Ex 8 B 1) Show that the differential equation is a solution of

Solution 2 Show that the differential equation Solution is a solution of
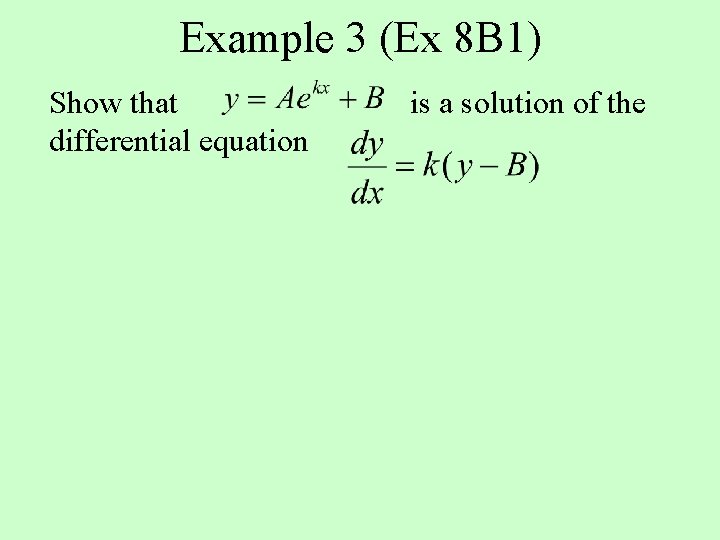
Example 3 (Ex 8 B 1) Show that differential equation is a solution of the

Solution 3 Show that the differential equation Solution is a solution of Now

Example 4 (Ex 8 B 2) Given the differential equation Find a, b, c and d given is the solution of

Solution 4 Given the differential equation Find a, b, c and d given Solution: is the solution of

Solution 4 continued
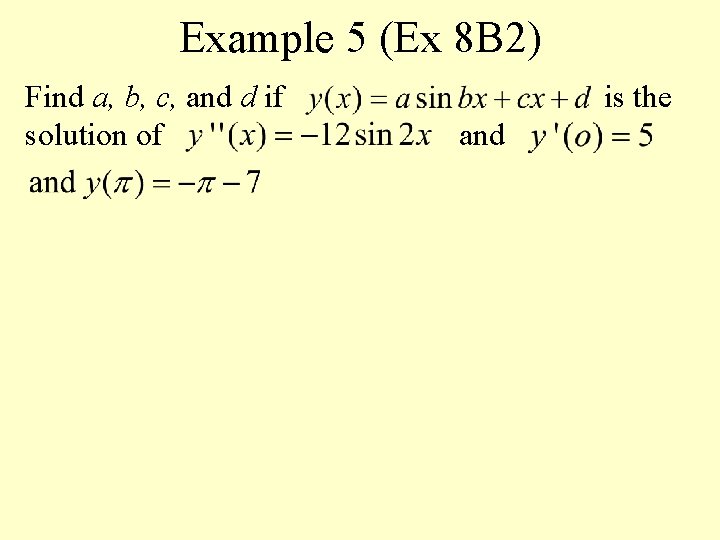
Example 5 (Ex 8 B 2) Find a, b, c, and d if solution of is the and

Solution 5 Find a, b, c, and d if the solution of Solution: is and
Solution 5 continued

Solution 5 continued again

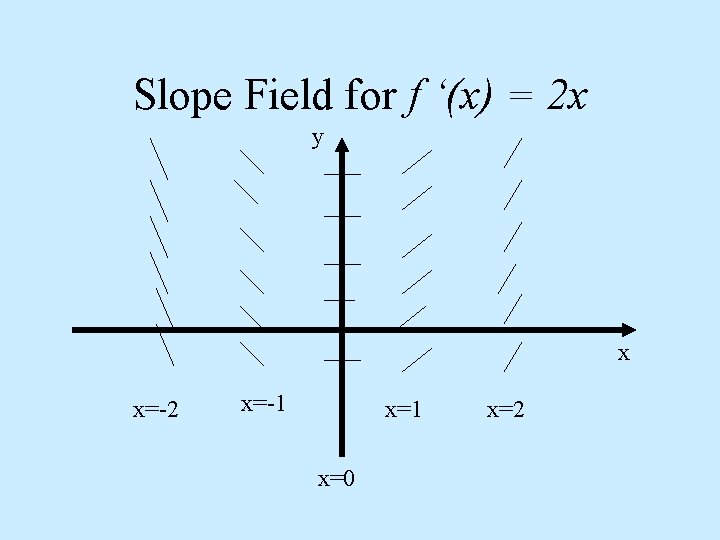
Slope Fields • The differential equation gives a formula for the slope its solutions. • For example the differential equation gives an equation to calculate the slopes of all points in the plane for functions whose derivatives are. • That is it gives the slopes of all points of functions of the form

Slope Field for f ‘(x) = 2 x y x x=-2 x=-1 x=0 x=2

Slope Field Generator http: //alamos. math. arizona. edu/ODEApplet/JOde. Applet. html • • • y’ = 2 x y‘ = 3 x 2 y’ = 2 x + 1 y’ = x y’ = y y’ = x + y for y = x 2 + c for y = x 3 + c for y = x 2 + x + c

Example 6 (Ex 8 C 1) Solve the following differential equation

Solution 6 Solve the following differential equation Solution:

Example 7 (Ex 8 C 1) Solve
Solution 7 Solve Solution
Solution 7 continued

Solution 7 continued again

Euler’s Method of Numerical Integration • We find the solution of a differential equation by moving small increments along the slope field • Start at (xo, yo), then move up the slope field and at the same time going out horizontally h to get to the next point (x 1, y 1). • The smaller the value of h the more accurate the solution.

Euler’s Method

Fundamental Theorem of Calculus • Using Euler’s method if we make the size of h very small then the y value of the point we approach is given by:

Example 8 (Ex 8 C 2) Use Euler’s method with 3 steps to find y(0. 6) for the differential equation with y(0)=2 Find y(6) using the Fundamental theorem

Solution 8 Use Euler’s method with 3 steps to find y(0. 6) for the differential equation with y(0)=2 Find y(6) using the Fundamental theorem Solution:
Solution 8 continued

Solution 8 continued again

This week • • • Exercise 8 A 1 Q 2, 3 Exercise 8 B 1 Q 1 – 7 Exercise 8 B 2 Q 1 – 7 Exercise 8 C 1 Q 1 – 7 Exercise 8 C 2 Q 1, 2
 Math specialist formula sheet
Math specialist formula sheet Kings college maths school
Kings college maths school Week by week plans for documenting children's development
Week by week plans for documenting children's development Higher maths trig equations
Higher maths trig equations Differential equations projects
Differential equations projects Bernoulli differential equation ppt
Bernoulli differential equation ppt Differential equations in computer science
Differential equations in computer science Cengage differential equations
Cengage differential equations Nonlinear ordinary differential equations
Nonlinear ordinary differential equations Transient solution differential equations
Transient solution differential equations Differential equations calculus
Differential equations calculus Examples of differential equation
Examples of differential equation Integrating factor of differential equation
Integrating factor of differential equation Partial differential equations examples
Partial differential equations examples What is a first order equation
What is a first order equation Solving 1st order differential equations
Solving 1st order differential equations Homogeneous differential equation examples
Homogeneous differential equation examples Cengage differential equations
Cengage differential equations Transient solution differential equations
Transient solution differential equations Runge kutta second order formula
Runge kutta second order formula Pde first order
Pde first order Classifying differential equations
Classifying differential equations Traffic flow differential equations
Traffic flow differential equations Midpoint method formula
Midpoint method formula Solution on
Solution on First order linear differential equation
First order linear differential equation First-order differential equations
First-order differential equations Hcc differential equations
Hcc differential equations Differential equations
Differential equations Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Bernoulli differential equation example
Bernoulli differential equation example Parachute problem differential equations
Parachute problem differential equations Application of homogeneous differential equation
Application of homogeneous differential equation Introduction to linear algebra strang
Introduction to linear algebra strang