snick snack CPSC 121 Models of Computation 2013

snick snack CPSC 121: Models of Computation 2013 W 2 Introduction to Induction Steve Wolfman 1

Outline • • Prereqs, Learning Goals, and Quiz Notes Bonus Prelude A Pattern for Induction Problems and Discussion – Single-Elimination Tournaments – Induction on Numbers • Next Lecture Notes 2

Learning Goals: Pre-Class By the start of class, you should be able to: – Convert sequences to and from explicit formulas that describe the sequence. – Convert sums to and from summation/“sigma” notation. – Convert products to and from product/“pi” notation. – Manipulate formulas in summation/product notation by adjusting their bounds, merging or splitting summations/products, and factoring out values. 5

Learning Goals: In-Class By the end of this unit, you should be able to: – Given a theorem to prove via induction and the insight into how the problem breaks down into one or more smaller problem(s), write out a complete proof strategy. – Prove naturally self-referential properties by induction. (That is, identify the “insight” and flesh out the strategy into a complete proof. ) 6

Where We Are in The Big Stories Theory Hardware How do we model computational systems? How do we build devices to compute? Now: Developing a new proof technique that’s perfect for algorithms involving recursion (or iteration). . . which is almost all interesting algorithms! Now: Taking a break in lecture. In lab, nearly at complete, working computer! (Although lab’s taking a break too, for regular expressions. ) 7

Outline • • Prereqs, Learning Goals, and Quiz Notes Bonus Prelude A Pattern for Induction Problems and Discussion – Single-Elimination Tournaments – Induction on Numbers • Next Lecture Notes 8

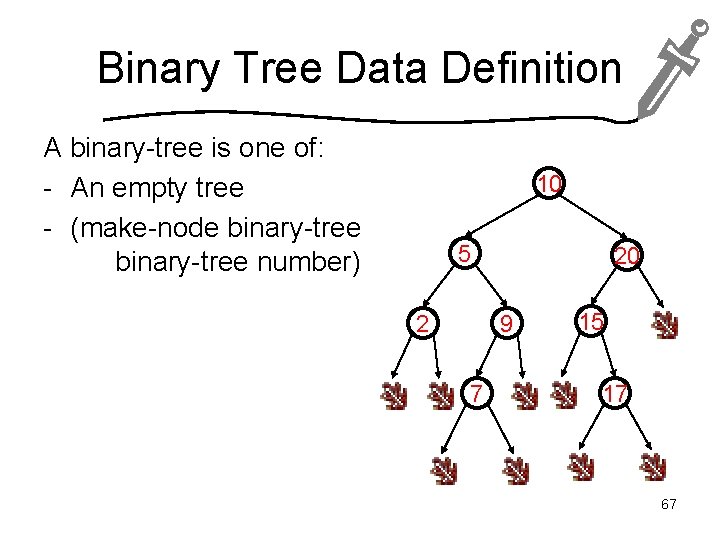
Prelude: A Binary Tree with n Nodes contains n+1 Empty Trees Note: We’ll define a binary tree as one of an empty tree or a “node” with two subtrees (each itself a binary tree). (What a “node” is depends on what we want to do with the tree but doesn’t concern us here!) Translate the definition and theorem to predicate logic; use the proofs sheet to think about how to prove it. 9

Induction: Regular Old Proof Plus One Powerful Step A binary tree is: an empty tree or a node with two subtrees (each itself a binary tree). Theorem: A binary tree with n nodes contains n+1 empty trees. Induction gives us one extra tool: 10 assuming our theorem holds for recursive sub-cases.

“Binary Trees” A “binary tree” is either an empty tree or a node with two children, each of which is a binary tree. 10 5 2 20 9 7 15 17 11 (They let us do some cool CS things. . . see CS 110, 221. )

New Proof Technique: (Structural) Induction 1. Identify the key recursive structure in the problem. For example, binary trees. A binary tree is one of: • An empty tree • A node with two subtrees, each of which is a binary tree The book discusses “weak” and “strong” induction. 12 As far as we are concerned, there can be only one induction: structural.

New Proof Technique: (Structural) Induction 2. Circle each recursive appearance of the structure inside its definition. A binary tree is one of: • An empty tree • A node with two subtrees, each of which is a binary tree 13 So, the two subtrees are recursive appearances of binary trees.

New Proof Technique: (Structural) Induction 3. Divide the cases into: those without recursive appearances (“base cases”) and those with (“recursive” or “inductive” cases) A binary tree is one of: • An empty tree Base case • A node with two subtrees, each of which Inductive case is a binary tree 14 Reuse all of these steps whenever you reuse the recursive structure.

New Proof Technique: (Structural) Induction 4. Write a predicate describing what you want to say about the structure. For example: P(t) ≡ the number of empty trees in the binary tree t is one more than the number of nodes in t 15 Always in terms of one of the recursive structure.

New Proof Technique: (Structural) Induction • 16 This step is easy!

New Proof Technique: (Structural) Induction 6. Write out your proof template: P(a) ≡ [fill in predicate definition] Theorem: For all [recursive structure] a, P(a) holds. Proof by structural induction: Base case: [For each base case you ID’d, write the structure of that case and prove theorem holds for that case. If you don’t END by showing your theorem true for the base case structure, 17 you probably messed up!]

Example P(t) ≡ the number of empty trees in the binary tree t is one more than the number of nodes in t Theorem: For all binary trees t, P(t) holds. Proof by structural induction: Base case: t is an empty tree. In that case, t has no nodes and one empty tree. 1 = 0 + 1 as expected. 18

New Proof Technique: (Structural) Induction 6. Proof template continued: Inductive Step: [For each recursive case write out an inductive step…] Consider an arbitrary [recursive case structure] a. Induction Hypothesis: Assume theorem holds for [each recursive appearance of the structure in this case]. We now show that theorem holds for a itself. 19

Example Inductive Step: Consider an arbitrary non-empty binary tree t (i. e. , a node with two subtrees, each of which is a binary tree). Induction Hypothesis: Assume theorem holds for the two subtrees of t. We now show that theorem holds for t itself. 20

New Proof Technique: (Structural) Induction 6. Proof template completed: [Show that theorem holds! Three signs that something has probably gone wrong: 1) You don’t END by showing that your theorem holds for a. 2) You don’t USE the “Induction Hypothesis” assumption(s) you made. 3) You EVER take a recursive appearance and use the recursive definition to break it down further (Example BAD thing to say: “Each of the subtrees is also a binary tree; so, it can have subtrees and so on until we reach an empty tree. )] 21

Example Consider an arbitrary binary tree t. Induction Hypothesis: Assume theorem holds for the two subtrees of t. t’s left subtree tl has some number of nodes nl and some number of empty trees el. By assumption, el = nl + 1. Similarly for t’s right subtree tr, er = nr + 1. t’s number of nodes n includes all of tl’s and tr’s nodes plus its own node. t’s number of empty trees e includes all and only the empty trees in tl and tr. Thus n = nl + nr + 1 and e = el + er. Substituting from above: e = el + er = n/ + 1 + nr + 1= nl + nr + 1 = n + 1. Thus, e = n + 1, as we wanted to prove. 22 QED

Outline • • Prereqs, Learning Goals, and Quiz Notes Bonus Prelude A Pattern for Induction Problems and Discussion – Single-Elimination Tournaments – Induction on Numbers • Next Lecture Notes 23

A Pattern for Induction 1. Identify the recursive structure in the problem. 2. Circle each recursive appearance of the structure inside its definition. 3. Divide the cases into: those without recursive appearances (“base cases”) and those with (“recursive” or “inductive” cases) 4. Write a predicate P(a) describing what you want to say about the structure. 5. Write your theorem a ? , P(a) 24 6. Complete the proof template.

P(a) ≡ [fill in predicate definition] Theorem: For all [recursive structure] a, P(a) holds. Proof by structural induction: Base case: [For each non-recursive case, prove theorem holds for that case. End by showing your theorem true for the base case structure!] Inductive Step: [For each recursive case…] Consider an arbitrary [recursive case structure] a. Induction Hypothesis: Assume theorem holds for [each recursive appearance of the structure in this case]. We now show theorem holds for a. [And then do so! You should: 1) END by showing that your theorem holds for a. 2) USE the “Induction Hypothesis” assumption(s) you made. 3) NEVER take a recursive appearance and use the recursive definition to break it down further, like this BAD example: “each subtree is a binary tree that can have subtrees and so on until we reach an empty tree. ”] It helps to write out what you want to prove rather than just “show theorem holds for a”. 25 (Even though neither one is strictly necessary. )

Outline • • Prereqs, Learning Goals, and Quiz Notes Bonus Prelude A Pattern for Induction Problems and Discussion – Single-Elimination Tournaments – Induction on Numbers • Next Lecture Notes 26

Single-Elimination Tournaments In each round teams play in pairs. Losing teams are eliminated. The tournament ends when only one team remains. 27

What is a Tournament? Let’s think like CPSC 110 ers… A tournament is one of: 28

The “insight into how the problem breaks down” A tournament of n rounds is made up of two tournaments of (n-1) rounds, like how the Stanley Cup Finals is set “on top of” the “east half” and “west half” tournaments. One extra round: east winner vs. west winner 29

Single-Elimination Tournament Problem What’s the maximum number of teams in a 0 -round single-elimination tournament? a. 0 teams b. 1 team c. 2 teams d. 3 teams e. None of these 30 Think: what does this correspond to in the data definition?

Single-Elimination Tournament Problem What’s the maximum number of teams in a 1 -round single-elimination tournament? a. 0 teams b. 1 team c. 2 teams d. 3 teams e. None of these A “one round tournament” has only one set of games. 31 A “two round tournament” has two sets of games (finals and semi-finals).

Single-Elimination Tournament Problem What’s the maximum number of teams in a 2 -round single-elimination tournament? a. 0 teams b. 1 team c. 2 teams d. 3 teams e. None of these Would there be any “byes” in the tournament? 32 A team with a “bye” gets to advance to the next round “for free”.

Single-Elimination Tournament Problem What’s the maximum number of teams in an n-round single-elimination tournament? a. n teams b. 2 n teams c. n 2 teams d. 2 n teams e. None of these (Induction is for proving our theorem; 33 it’s not for figuring out what we want to prove!)

A Pattern for Induction • Coincidentally, t’s a good variable name again! 34

Side Note: How Many Rounds Does a Tournament Have? How many rounds does a tournament that’s just a single winner have? How many rounds does a tournament that’s a final game between the winners of two smaller tournaments have? 35

Side Note: How Many Rounds Does a Tournament Have? A tournament has: • 0 rounds if it’s just a single “winner” • 1 more round than the largest number of rounds of either of its subtournaments, otherwise 36

P(a) ≡ [fill in predicate definition] Theorem: For all [recursive structure] a, P(a) holds. Proof by structural induction: Base case: [For each non-recursive case, prove theorem holds for that case. End by showing your theorem true for the base case structure!] Inductive Step: [For each recursive case…] Consider an arbitrary [recursive case structure] a. Induction Hypothesis: Assume theorem holds for [each recursive appearance of the structure in this case]. We now show theorem holds for a. [And then do so! You should: 1) END by showing that your theorem holds for a. 2) USE the “Induction Hypothesis” assumption(s) you made. 3) NEVER take a recursive appearance and use the recursive definition to break it down further, like this BAD example: “each subtree is a binary tree that can have subtrees and so on until we reach an empty tree. ”] 37

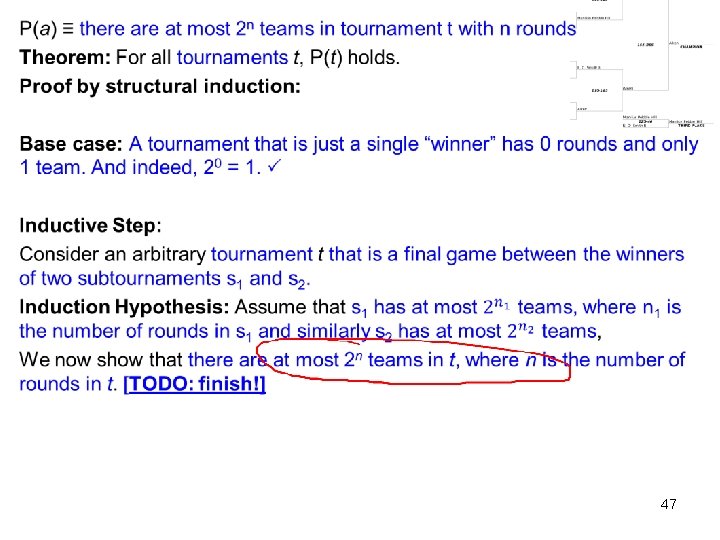
P(a) ≡ there at most 2 n teams in tournament t with n rounds Theorem: For all [recursive structure] a, P(a) holds. Proof by structural induction: Base case: [For each non-recursive case, prove theorem holds for that case. End by showing your theorem true for the base case structure!] Inductive Step: [For each recursive case…] Consider an arbitrary [recursive case structure] a. Induction Hypothesis: Assume theorem holds for [each recursive appearance of the structure in this case]. We now show theorem holds for a. [And then do so! You should: 1) END by showing that your theorem holds for a. 2) USE the “Induction Hypothesis” assumption(s) you made. 3) NEVER take a recursive appearance and use the recursive definition to break it down further, like this BAD example: “each subtree is a binary tree that can have subtrees and so on until we reach an empty tree. ”] 38

P(a) ≡ there at most 2 n teams in tournament t with n rounds Theorem: For all tournaments t, P(t) holds. Proof by structural induction: Base case: [For each non-recursive case, prove theorem holds for that case. End by showing your theorem true for the base case structure!] Inductive Step: [For each recursive case…] Consider an arbitrary [recursive case structure] t. Induction Hypothesis: Assume theorem holds for [each recursive appearance of the structure in this case]. We now show theorem holds for t. [And then do so! You should: 1) END by showing that your theorem holds for t. 2) USE the “Induction Hypothesis” assumption(s) you made. 3) NEVER take a recursive appearance and use the recursive definition to break it down further, like this BAD example: “each subtree is a binary tree that can have subtrees and so on until we reach an empty tree. ”]39 I changed all the variables to t just because t’s a good name for a tournament.

P(a) ≡ there at most 2 n teams in tournament t with n rounds Theorem: For all tournaments t, P(t) holds. Proof by structural induction: Base case: A tournament that is just a single “winner”… [TODO: finish!] Inductive Step: [For each recursive case…] Consider an arbitrary [recursive case structure] t. Induction Hypothesis: Assume theorem holds for [each recursive appearance of the structure in this case]. We now show theorem holds for t. [And then do so! You should: 1) END by showing that your theorem holds for t. 2) USE the “Induction Hypothesis” assumption(s) you made. 3) NEVER take a recursive appearance and use the recursive definition to break it down further, like this BAD example: “each subtree is a binary tree that can have subtrees and so on until we reach an empty tree. ”] 40 We’ll leave the proof of the base case until we’ve finished the structural pieces.

P(a) ≡ there at most 2 n teams in tournament t with n rounds Theorem: For all tournaments t, P(t) holds. Proof by structural induction: Base case: A tournament that is just a single “winner”… [TODO: finish!] Inductive Step: Consider an arbitrary [recursive case structure] t. Induction Hypothesis: Assume theorem holds for [each recursive appearance of the structure in this case]. We now show theorem holds for t. [And then do so! You should: 1) END by showing that your theorem holds for t. 2) USE the “Induction Hypothesis” assumption(s) you made. 3) NEVER take a recursive appearance and use the recursive definition to break it down further, like this BAD example: “each subtree is a binary tree that can have subtrees and so on until we reach an empty tree. ”] 41 There’s just the one recursive case.

P(a) ≡ there at most 2 n teams in tournament t with n rounds Theorem: For all tournaments t, P(t) holds. Proof by structural induction: Base case: A tournament that is just a single “winner”… [TODO: finish!] Inductive Step: Consider an arbitrary tournament t that is a final game between the winners of two subtournaments (which we’ll call s 1 and s 2). Induction Hypothesis: Assume theorem holds for [each recursive appearance of the structure in this case]. We now show theorem holds for t. [And then do so! You should: 1) END by showing that your theorem holds for t. 2) USE the “Induction Hypothesis” assumption(s) you made. 3) NEVER take a recursive appearance and use the recursive definition to break it down further, like this BAD example: “each subtree is a binary tree that can have subtrees and so on until we reach an empty tree. ”] It’s often handy to name those recursive appearances! 42 E. g. , subtournaments s 1 and s 2.

P(a) ≡ there at most 2 n teams in tournament t with n rounds Theorem: For all tournaments t, P(t) holds. Proof by structural induction: Base case: A tournament that is just a single “winner”… [TODO: finish!] Inductive Step: Consider an arbitrary tournament t that is a final game between the winners of two subtournaments s 1 and s 2. Induction Hypothesis: Assume theorem holds for s 1 and s 2. We now show theorem holds for t. [And then do so! You should: 1) END by showing that your theorem holds for t. 2) USE the “Induction Hypothesis” assumption(s) you made. 3) NEVER take a recursive appearance and use the recursive definition to break it down further, like this BAD example: “each subtree is a binary tree that can have subtrees and so on until we reach an empty tree. ”] 43

• 44 It helps to write out what you want to prove rather than just “show theorem holds for a”.

The “insight into how the problem breaks down” The n-round tournament with the maximum number of teams is made from two (n-1)-round tournaments with the maximum number of teams. 49

Step-by-Step? Here’s the logical structure of our theorems: MT(0, 20). n Z 0, (n > 0) MT(n-1, 2 n-1) MT(n, 2 n). Do these prove MT(1, 21)? a. Yes. b. No. c. I don’t know. 50

Step-by-Step? Here’s the logical structure of our theorems: MT(0, 20). n Z 0, (n > 0) MT(n-1, 2 n-1) MT(n, 2 n). Plus, we know MT(1, 21). Do all of these prove MT(2, 22)? a. Yes. b. No. c. I don’t know. 51

Step-by-Step? Here’s the logical structure of our theorems: MT(0, 20). n Z 0, (n > 0) MT(n-1, 2 n-1) MT(n, 2 n). Plus, we know MT(1, 21) and MT(2, 22). Do all of these prove MT(3, 23)? a. Yes. b. No. c. I don’t know. 52

Step-by-Step? Here’s the logical structure of our theorems: MT(0, 20). n Z 0, (n > 0) MT(n-1, 2 n-1) MT(n, 2 n). From this, can we prove MT(n, 2 n) for any particular integer n? a. Yes. b. No. c. I don’t know. 53

The Magic of Induction! Our “proof” is really a recursive program. Plug in a tournament of a particular number of rounds n, and it produces a proof that tournament cannot have more than 2 n teams in it. The magic of induction is that we agree that writing this program is the same as writing all the proofs the program can create. 54

Outline • • Prereqs, Learning Goals, and Quiz Notes Bonus Prelude A Pattern for Induction Problems and Discussion – Single-Elimination Tournaments – Induction on Numbers • Next Lecture Notes 55

Natural Numbers and Induction Can we prove things inductively about the natural numbers without a recursive data definition? Are they “self-referential”? Here’s one answer: A natural number is: - 0 - The next number after (successor of) a natural number 56

Natural Numbers and Induction Can we prove things inductively about the natural numbers without a recursive data definition? Are they “self-referential”? But, let’s just try one! Problem: What is the sum of the natural numbers 0. . n? 57

Partly Worked Problem: Sum of 0. . n Partly Worked Problem: What is the sum of the natural numbers 0. . n? Induction doesn’t help with insight. . . But spoilers do: n(n+1)/2. Now, how do we prove it? 58

Partly Worked Problem: Sum of 0. . n Partly Worked Problem: Prove that the sum of the natural numbers 0. . n is n(n+1)/2. Is this self-referential? If we knew the sum of the numbers 0. . (n-1), would it tell us anything about the sum of the numbers 0. . n? 59

Sigma, Pi, Factorial, Powers: All Self-Referential 60 So? So, you can do inductive proofs on them!

Outline • • Prereqs, Learning Goals, and Quiz Notes Bonus Prelude A Pattern for Induction Problems and Discussion – Single-Elimination Tournaments – Induction on Numbers • Next Lecture Notes 61

Learning Goals: In-Class By the end of this unit, you should be able to: – Establish properties of self-referential structures using inductive proofs that naturally build on those self-references. Note: this learning goal is not yet looking formal inductive proofs. Instead, we’re just exploring how we work with things that are defined in terms of themselves. 62

Next Lecture Learning Goals: Pre-Class By the start of class, you should be able to: – Given a theorem to prove and the insight into how to break the problem down in terms of smaller problems, write out the skeleton of an inductive proof including: the base case(s) that need to be proven, the induction hypothesis, and the inductive step that needs to be proven. So, take what we did in this lecture and use the textbook readings to formalize your understanding. 63 We will have much more practice on inductive proofs.

Next Lecture Prerequisites See the Mathematical Induction Textbook Sections at the bottom of the “Textbook and References” page. 64

snick snack Extra Slides 65

One Extra Step We Sometimes Do Really, we are done. But just to be thorough, we’ll add: Termination: the number of rounds n is a non-negative integer, and each application of the inductive step reduces it by at least 1. Therefore, it must reach our base case (0) in a finite number of steps. 66

Binary Tree Data Definition A binary-tree is one of: - An empty tree - (make-node binary-tree number) 10 5 2 20 9 7 15 17 67

10 Binary Trees’ Height 5 2 20 9 15 7 17 A binary tree’s “height” is the maximum number of steps it takes to get from the root down to a node with only empty trees as children. This one’s height is: a. 0 b. 1 c. 2 d. 3 e. 4 68

10 Binary Trees’ Height 5 2 20 15 9 7 17 Problem 1: What’s the maximum number of nodes in a binary tree of height n? 69

10 Binary Trees’ Height 5 2 20 9 15 7 17 Problem 2: Prove your result. 70

Binary Trees, Take Two 10 5 2 20 9 15 7 17 Problem 1: Give an algorithm to determine the height of a binary tree. Problem 2: Prove that your algorithm is correct. 71

10 5 Worked: Algorithm for Height 2 9 7 20 15 17 Height(t): Is t an empty tree? Yes: evaluate to -1 No: recursively find the height of each subtree hl and hr and evaluate to max(hl, hr) + 1. How big are the subtrees? 72 We need to assume the algorithm works on trees of “those sizes”.

Worked: Proof of Algorithm’s Correctness 10 5 2 20 9 7 15 17 Proof: We proceed by induction. Base case: On an empty tree, our algorithm yields -1. We simply make this correct by definition. (Or, you can imagine we go “up one level” to get to a node. ) Induction Hypothesis: For an arbitrary (finite-sized) non-empty tree t, assume our algorithm works correctly on all trees smaller than t. Inductive step: t is not an empty tree; so, our algorithm finds the height of each subtree hl and hr. These heights are correct by assumption, since the subtrees must be smaller than t (lacking at least t itself!). To reach a node with only leaves as children, we go into either the left or right subtree. The length of the path through the left subtree is therefore hl+1, with the +1 for the step down into that subtree. Similarly, the right path is hr +1. The height is the larger of these possible paths; so, it’s max(hl+1, hr+1) = max(hl, hr) + 1, which is what our algorithm evaluates to. Termination: We call this only on finite trees, and we reduce the size of the tree by at least one node at each inductive step. Thus, we eventually reach an empty tree. 73 QED