snick snack CPSC 121 Models of Computation 2013

snick snack CPSC 121: Models of Computation 2013 W 2 Sets Steve Wolfman, based on notes by Patrice Belleville and others 1

Outline • • Prereqs, Learning Goals, and Quiz Notes Out-of-class notes on set definitions What’s the Use of Sets (history & DFAs) More set operations – Cardinality (size) – Power set (and an induction proof) – Cartesian products (and application to DFAs) • Set proofs • Next Lecture Notes 2

Learning Goals: Pre-Class By the start of class, you should be able to: – Define the set operations union, intersection, complement, and set difference and the logical operations subset and set equality in terms of predicate logic and set membership ( ). – Translate between sets represented explicitly (possibly using ellipses “…”, e. g. , {4, 6, 8, …}) and using “set builder” notation (e. g. , {x Z+ | x 2 > 2 x is even}). – Execute the union, intersection, complement, set difference, subset, and set equality operations on sets expressed explicitly, using set builder notation, or a combination of these and set operators. – Interpret the empty set symbol , including the fact that the empty set has no members and that it is a subset of any set. 3

Learning Goals: In-Class By the end of this unit, you should be able to: – Define the power set and cartesian product operations in terms of predicate logic and set membership/subset relations. – Execute the power set, cartesian product, and cardinality operations on sets expressed through any of the notations discussed so far. – Apply your proof skills to proofs involving sets. – Relate DFAs to sets. 4

CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) Outline • • Prereqs, Learning Goals, and Quiz Notes Out-of-class notes on set definitions What’s the Use of Sets (history & DFAs) More set operations – Cardinality (size) – Power set (and an induction proof) – Cartesian products (and application to DFAs) • Set proofs • Next Lecture Notes 5

Outline • • Prereqs, Learning Goals, and Quiz Notes Out-of-class notes on set definitions What’s the Use of Sets (history & DFAs) More set operations – Cardinality (size) – Power set (and an induction proof) – Cartesian products (and application to DFAs) • Set proofs • Next Lecture Notes 26

What Are Sets Good For? Historically: Mathematicians attempted to formalize set theory to create a foundation for all of mathematics. Essentially all mathematical constructs can be defined in terms of sets. Good news: this means sets are a powerful way to communicate many types of ideas. 27

Bad News: Russell’s Paradox (and other problems) Does the “set of all sets that contain themselves” contain itself? a. Yes, definitely. b. Maybe, either way is fine. c. No, definitely not. d. None of these. 28

Bad News: Russell’s Paradox (and other problems) Does the “set of all sets that do not contain themselves” contain itself? a. Yes, definitely. b. Maybe, either way is fine. c. No, definitely not. d. None of these. Same question, different form: “Imagine a barber that shaves every man in town 29 who does not shave himself. Does the barber shave himself? ”

What Are Sets Good For? Applications for us: Codifying and communicating ideas. For example, formalizing DFAs. . . 30

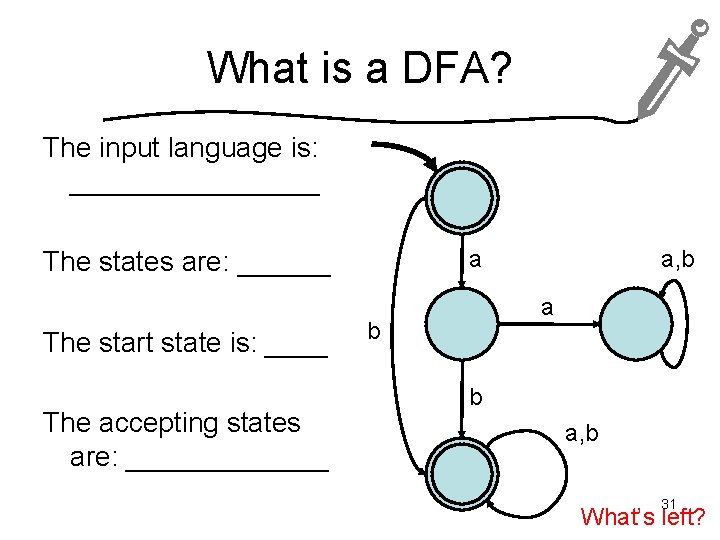
What is a DFA? The input language is: ________ a The states are: ______ The start state is: ____ The accepting states are: _______ a, b a b b a, b 31 What’s left?

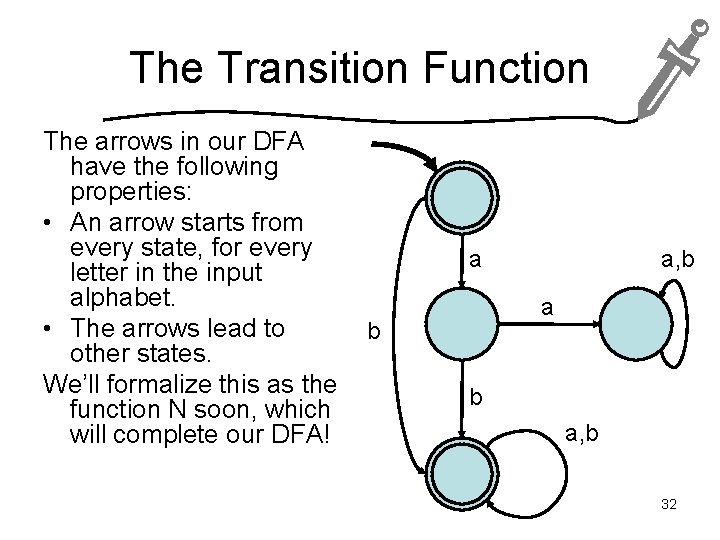
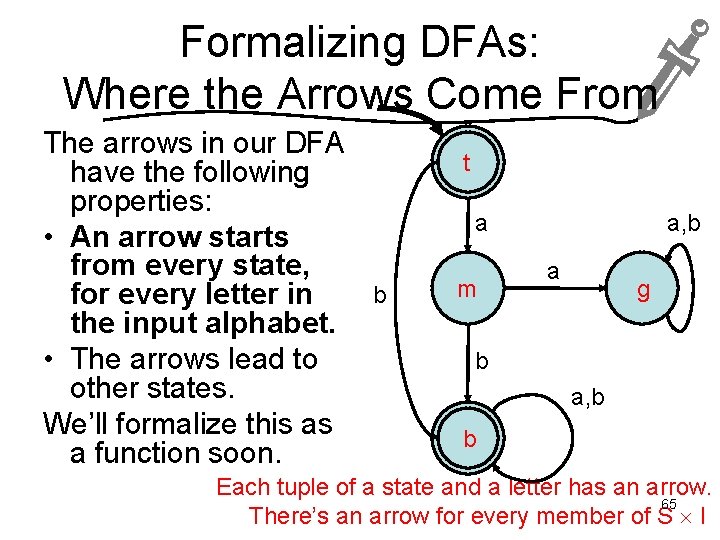
The Transition Function The arrows in our DFA have the following properties: • An arrow starts from every state, for every letter in the input alphabet. • The arrows lead to other states. We’ll formalize this as the function N soon, which will complete our DFA! a a, b a b b a, b 32

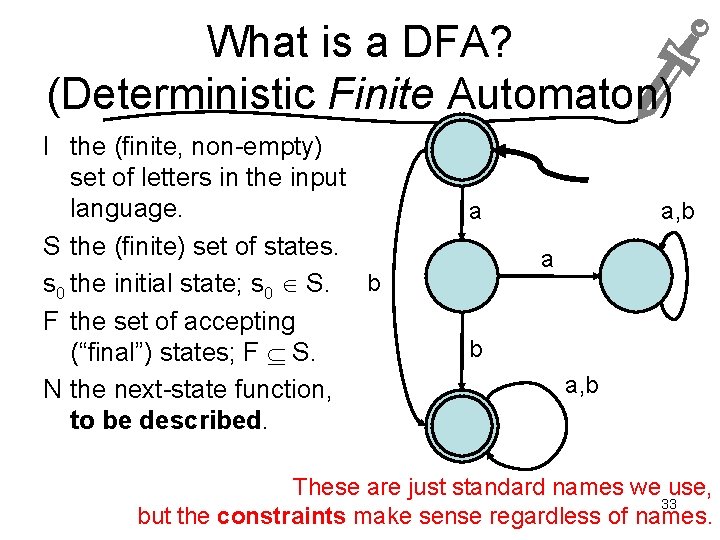
What is a DFA? (Deterministic Finite Automaton) I the (finite, non-empty) set of letters in the input language. S the (finite) set of states. s 0 the initial state; s 0 S. b F the set of accepting (“final”) states; F S. N the next-state function, to be described. a a, b These are just standard names we use, 33 but the constraints make sense regardless of names.

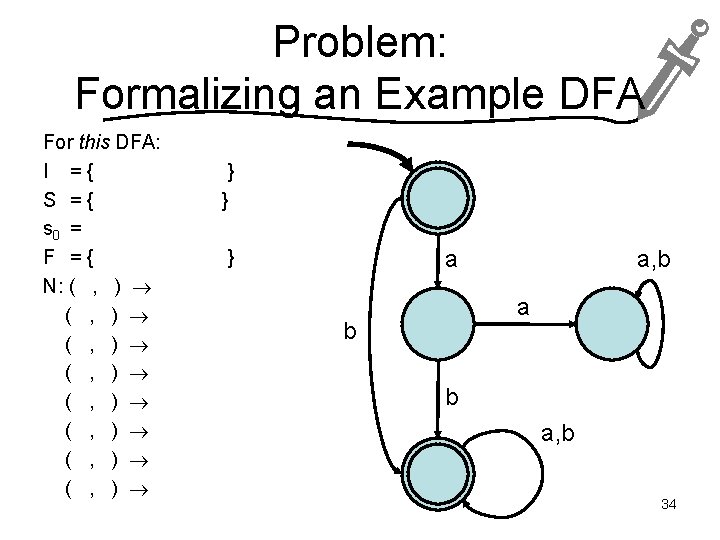
Problem: Formalizing an Example DFA For this DFA: I ={ S ={ s 0 = F ={ N: ( , ) ( , ) } } a, b a b b a, b 34

Problem: Testing the DFA Formalism I the (finite, non-empty) set of letters in the input language. S the (finite) set of states. s 0 the initial state; s 0 S. F the set of accepting (“final”) states; F S. N the next-state function, to be described. a. Yes b. No Must a DFA have an initial state? Can a DFA have more than one initial state? Must a DFA have an accepting state? Can all states in a DFA be accepting? Can the initial state be accepting? 36 c. Not enough information.

Testing the DFA Formalism Must a DFA have an initial state? Can a DFA have more than one initial state? Must a DFA have an accepting state? Can all states in a DFA be accepting? Can the initial state be accepting? s 0 is the initial state; so, yes. s 0 is the only initial state; so, no. F S. Is S? F S. Is S S? s 0 S and F S. Can s 0 F? 37

Must a DFA Have an Accepting State? What does a DFA with no accepting states look like? What language does it accept? 38

Can All States in a DFA Be Accepting? What does a DFA with no rejecting states look like? What language does it accept? 39

Outline • • Prereqs, Learning Goals, and Quiz Notes Out-of-class notes on set definitions What’s the Use of Sets (history & DFAs) More set operations – Cardinality (size) – Power set (and an induction proof) – Cartesian products (and application to DFAs) • Set proofs • Next Lecture Notes 40

Cardinality The cardinality of a set A — denoted |A| — is the set’s size. For finite sets, the cardinality of the set is the number of elements it contains… |A| |B| |C| |D| = = |{1, 3}| = 2 |{1, 3, 27, snow}| = 4 |{ {1, 3}, {1, 3, 27, snow} }| = 2 | | = 0 41

How Big Is a Set? How big are these sets? A B C D E F = = = a. 0 {1, 3} {1, 3, 27, snow} { {1, 3}, {1, 3, 27, snow} } N { …, -4, -2, 0, 2, 4, … } b. 1 c. 2 d. 3 42 e. None of these

Cardinality of Infinite Sets? For now, we won’t worry about the cardinality of infinite sets. Why? Well, we can’t count the members of such sets. Side note: Depending on our definition, however, the results can be surprising. For example, under the standard definition of cardinality, these have the same cardinality: E = N = {1, 2, 3, … } F = { …, -4, -2, 0, 2, 4, … } 43 Why? Try “folding” the set F over creatively.

Problem: Cardinality Exercises Given the definitions: A = {1, 2, 3} B = {2, 4, 6, 8} What are: |A| |B| |A B| a. 0 = = _________ b. 1 c. 2 |A – B| |B – A| |{{}}| |{{ }}| d. 3 = = = _________ _____ 44 e. None of these

Outline • • Prereqs, Learning Goals, and Quiz Notes Out-of-class notes on set definitions What’s the Use of Sets (history & DFAs) More set operations – Cardinality (size) – Power set (and an induction proof) – Cartesian products (and application to DFAs) • Set proofs • Next Lecture Notes 46

A Touch of Logic Consider the four propositional logic variables p, q, r, and s. What are all the different ways we can assign truth values to each of these? Now, imagine a set S that contains exactly the true variables among p, q, r, and s. What are the possible “Ss” (depending on p, q, r, and s’s truth values)? 47

A Touch of Logic: Rephrased Consider the set {p, q, r, s}. What are all the subsets of this set? Equivalently, what is: {S U | S {p, q, r, s}}? 48

Power Sets The power set of a set T — denoted P(T) — is the set of all subsets of T: { S U | S T } 49

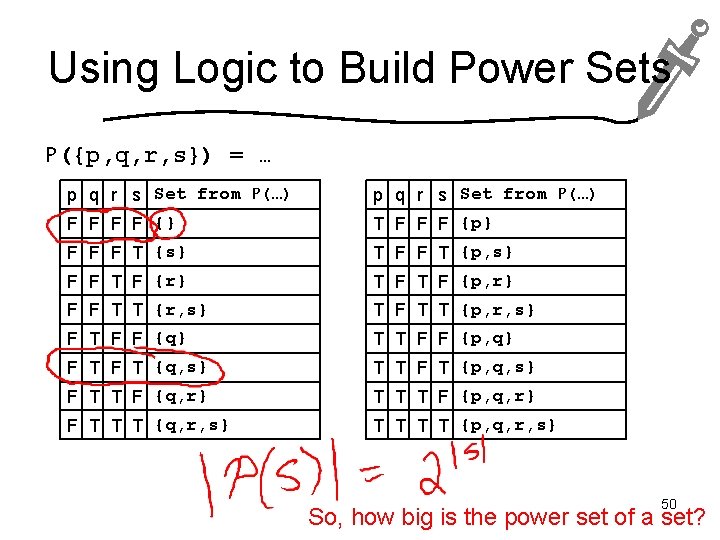
Using Logic to Build Power Sets P({p, q, r, s}) = … p q r s Set from P(…) F F {} T F F F {p} F F F T {s} T F F T {p, s} F F T F {r} T F {p, r} F F T T {r, s} T F T T {p, r, s} F T F F {q} T T F F {p, q} F T {q, s} T T F T {p, q, s} F T T F {q, r} T T T F {p, q, r} F T T T {q, r, s} T T {p, q, r, s} 50 So, how big is the power set of a set?

Cardinality of a Finite Power Set Theorem: |P(S)| = 2|S| Base case: When |S| = 0, what is S? What is P(S)? How do we know? 53

Cardinality of a Finite Power Set Inductive Hypothesis: Assume for all sets S of cardinality k 0, |P(S)| = 2|S|. Inductive step: To prove: Given the induction hypothesis, for all sets T, |P(T)| = 2|T| when |T| = k+1. The key is to drop an element from a set of size k+1. Then, take the power 54 set. Then, consider how to put the element back in.

Outline • • Prereqs, Learning Goals, and Quiz Notes Out-of-class notes on set definitions What’s the Use of Sets (history & DFAs) More set operations – Cardinality (size) – Power set (and an induction proof) – Cartesian products (and application to DFAs) • Set proofs • Next Lecture Notes 58

Tuples A tuple is an ordered collection of elements. (An n-tuple is a tuple with n elements. ) Two tuples are equal when each pair of corresponding elements is the same: (a, 1, ) = (a, 5 – 4, A A) (a, b, c) (a, c, b) Actual fact: database people love the word “tuple”. 59 And… why shouldn’t they? Say “two-tuple”. Isn’t that great?

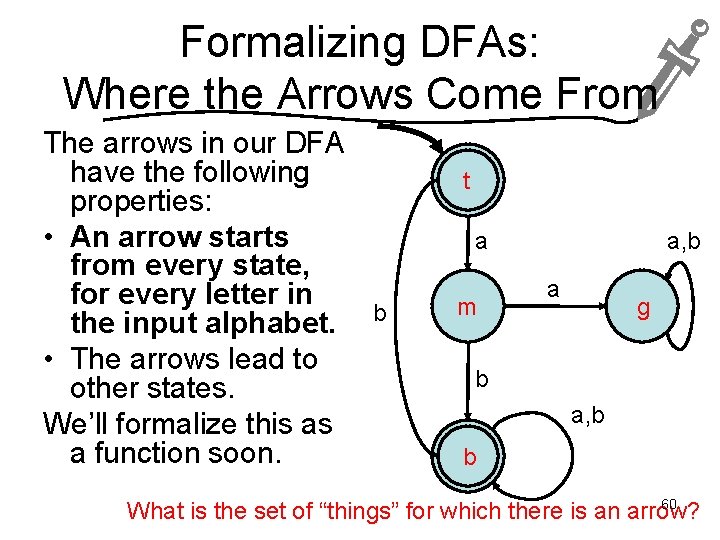
Formalizing DFAs: Where the Arrows Come From The arrows in our DFA have the following properties: • An arrow starts from every state, for every letter in the input alphabet. • The arrows lead to other states. We’ll formalize this as a function soon. t a b m a, b a g b a, b b 60 What is the set of “things” for which there is an arrow?

Cartesian Products The Cartesian product of the sets A and B — denoted A B — is the set of all tuples whose first element is drawn from A and whose second element is drawn from B. In other words, A B = {(a, b) | a A b B} 61

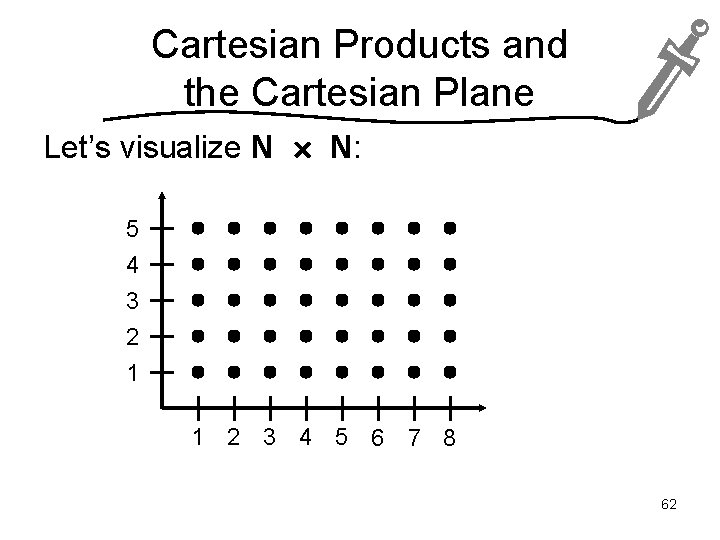
Cartesian Products and the Cartesian Plane Let’s visualize N N: 5 4 3 2 1 1 2 3 4 5 6 7 8 62

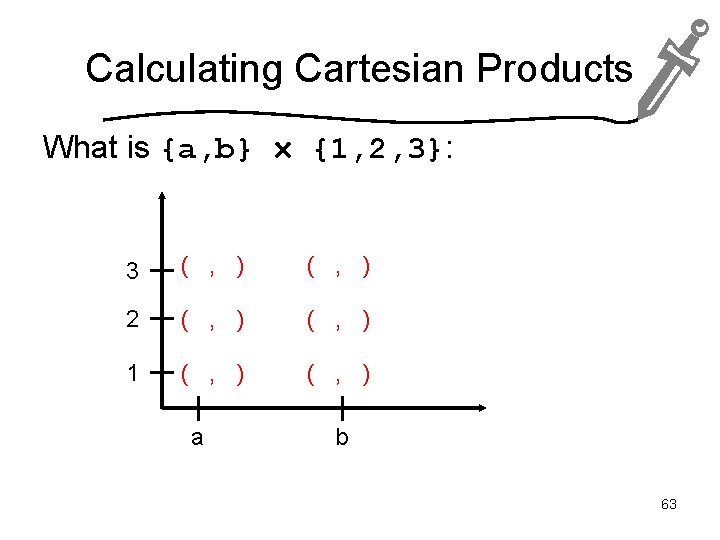
Calculating Cartesian Products What is {a, b} {1, 2, 3}: 3 ( , ) 2 ( , ) 1 ( , ) a b 63

Formalizing DFAs: Where the Arrows Come From The arrows in our DFA have the following properties: • An arrow starts from every state, for every letter in the input alphabet. • The arrows lead to other states. We’ll formalize this as a function soon. t a b m a, b a g b a, b b Each tuple of a state and a letter has an arrow. 65 There’s an arrow for every member of S I

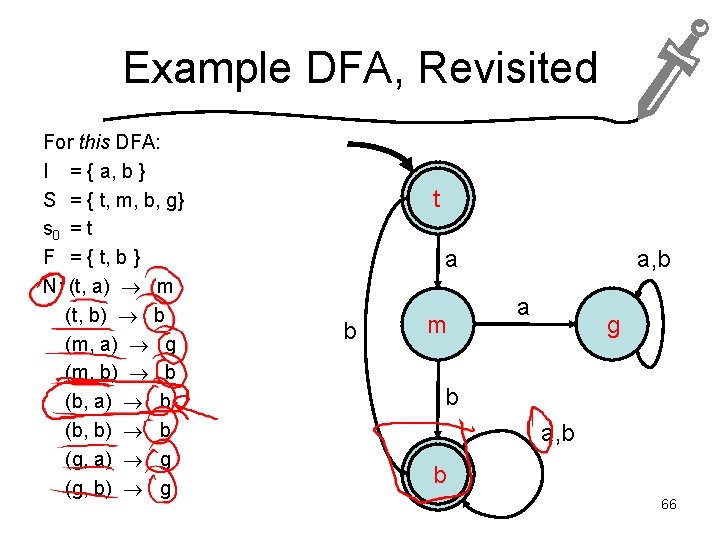
Example DFA, Revisited For this DFA: I = { a, b } S = { t, m, b, g} s 0 = t F = { t, b } N: (t, a) m (t, b) b (m, a) g (m, b) b (b, a) b (b, b) b (g, a) g (g, b) g t a b m a, b a g b a, b b 66

Outline • • Prereqs, Learning Goals, and Quiz Notes Out-of-class notes on set definitions What’s the Use of Sets (history & DFAs) More set operations – Cardinality (size) – Power set (and an induction proof) – Cartesian products (and application to DFAs) • Set proofs • Next Lecture Notes 67

Problem: Proofs with Sets (1/2) Prove by contradiction that for all sets A and B, if A B then A B = { }. (Note: B contains all elements in the universe that are not in B. ) 68

CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) Containment A set A is a subset of a set B iff x U, x A x B. We write A is a subset of B as A B. If A B, can B have elements that are not elements of A? Yes, but A can’t have elements that are not elements of B. 69

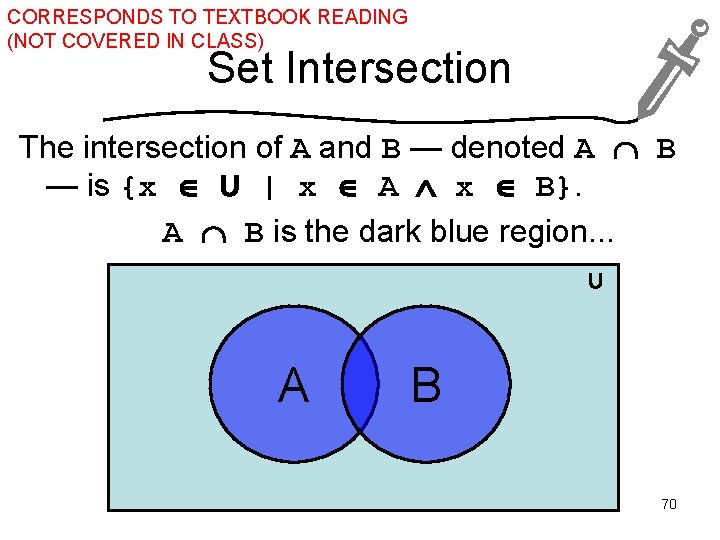
CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) Set Intersection The intersection of A and B — denoted A B — is {x U | x A x B}. A B is the dark blue region. . . U A B 70

CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) Set Complement The complement of A — denoted A — is {x U | x A}. A is everything but the blue region. U A 71 Can we express this as a set difference?

Problem: Proofs with Sets (2/2) Prove for all sets A and B, if A B then P(A) P(B). (Note: if A B and B C, then A C. ) 72

Power Sets The power set of a set T — denoted P(T) — is the set of all subsets of T: { S U | S T } 73

Outline • • Prereqs, Learning Goals, and Quiz Notes Out-of-class notes on set definitions What’s the Use of Sets (history & DFAs) More set operations – Cardinality (size) – Power set (and an induction proof) – Cartesian products (and application to DFAs) • Set proofs • Next Lecture Notes 74

Learning Goals: In-Class By the end of this unit, you should be able to: – Define the power set and cartesian product operations in terms of predicate logic and set membership/subset relations. – Execute the power set, cartesian product, and cardinality operations on sets expressed through any of the notations discussed so far. – Apply your proof skills to proofs involving sets. – Relate DFAs to sets. 75

Next Lecture Learning Goals: Pre-Class By the start of class, you should be able to: – Define the terms domain, co-domain, range, image, and pre-image – Use appropriate function syntax to relate these terms (e. g. , f : A B indicates that f is a function mapping domain A to codomain B). – Determine whether f : A B is a function given a definition for f as an equation or arrow diagram. 76

Next Lecture Prerequisites See the “Functions” readings on the “Textbook and References” section of the website. Complete the quiz on Vista before class. 77

snick snack Extra Slides: Worked Proofs (Thanks to Meghan Allen) 78

Proofs with Sets #1 version 1 Prove that for all sets A and B: A B = A B Proof #1: A B = = = {x U | x (A B)} Def’n of {x U | ~(x A x B)} Def’n of {x U | x A x B} De Morgan’s {x U | x A x B} Def’n of A B 79

Proofs with Sets #1 version 2 Remember that for any two sets C and D, C = D iff C is a subset of D and D is a subset of C. C = D [C D D C] 80

Proofs with Sets #1 version 2 a) Prove that: A B Pick an arbitrary x A B, Then x A B. Def’n of ~(x A x B) Def’n of x A x B De Morgan’s Def’n of x A x B Def’n of x (A B) 81

Proofs with Sets #1 version 2 b) Prove that: A B Pick an arbitrary x A B Then, x A x B ~(x A x B) x A B x A B 82

Proofs with Sets #1 version 2 conclusion We have shown that A B and A B. Therefore, A B = A B. 83

Proof with Sets #2 Prove that, for all sets A, B and C: (A B) – C = (A – C) (B – C) This time we’ll use the Set Identities LHS: (A B) – C = (A B) C = C (A B) = (C A) (C B) Set Difference Law = (A C) (B C) = (A - C) (B – C) Commutative Law Distributive Law Set Difference Law 84

Proofs with Sets #3 Prove or disprove, for all sets A and B, A–B=B–A We can disprove this with a counterexample. Let A = {1, 2} and B = {2, 3} Then, A-B = {1} and B-A = {3} A–B≠B–A 85

Proofs with Sets #4 Prove that for all sets A and B, if A B then A B = Proof by contradiction. Assume A B and A B . Then, there exists an element x A B. By the definition of intersection, that means x A and x B. Since x B, x B by the definition of complement. But, A B, so since x A, x B by definition of subset. Thus, x B and x B which is a contradiction. Hence the assumption is false and therefore for all sets A and B, if A B then A B = 86

Proofs with Sets #5 Prove that for all sets A and B, if A B then P A) P(B) WLOG, let A and B be sets. Proof by antecedent assumption: Assume A B. Now, consider X P(A). X A by the definition of power set. But, because A B, X B by the transitive property of subsets* and thus, by the definition of power set, X P(B). This proves that for all X, if X P(A) then X P(B) and so P(A) 87 P(B). *Epp -Theorem 5. 2. 1

Proofs with Sets #6 version 1 Prove that for all sets S, S. We proceed by contradiction. Assume that there is a set S such that the empty set is not a subset of S. Then, by definition of subset, there must be some element x of the empty set that is not an element of S. However, the empty set has no elements. This is a contradiction. QED 88

Proofs with Sets #6 version 2 Prove that for all sets S, S. Note that S x U, x x S. We proceed by proving this last statement. We know nothing is an element of the empty set: x U, x . By generalization, it follows that: x U, x x S. QED 89