SISTEMI DEQUAZIONI ED EQUAZIONI DIFFERENZIALI LINEARI Argomenti della














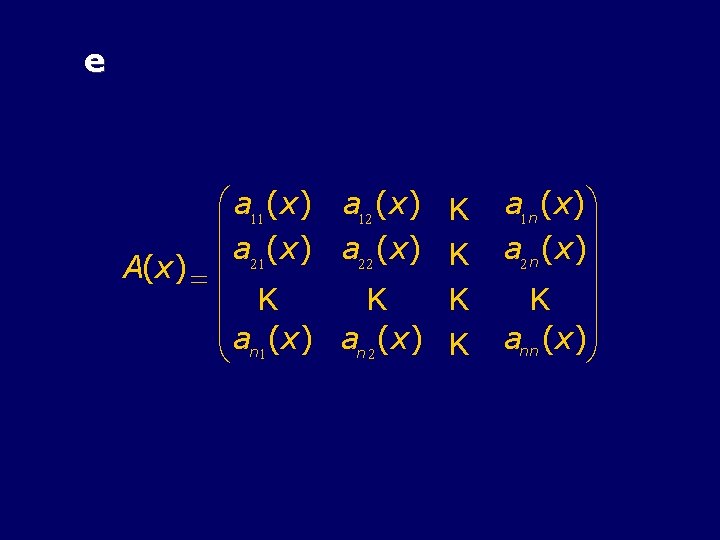



























- Slides: 43

SISTEMI D’EQUAZIONI ED EQUAZIONI DIFFERENZIALI LINEARI

Argomenti della lezione è Equazioni e sistemi d’equazioni differenziali ordinarie è Sistemi d’equazioni differenziali ordinarie lineari a coefficienti continui

EQUAZIONI E SISTEMI D’EQUAZIONI DIFFERENZIALI ORDINARIE

Mostreremo, per iniziare, che un’equazione differenziale d’ordine n è equivalente a un sistema d’equazioni differenziali del prim’ordine di n equazioni in n funzioni incognite. Sarà così plausibile la nostra affermazione che ogni sistema d’equazioni differenziali d’ordine qualsiasi è equivalente a un sistema d’equazioni del prim’ordine in un numero opportuno di funzioni incognite.

Un sistema d’equazioni differenziali di due equazioni in due funzioni incognite d’ordine 3 è per esempio il seguente (di forma normale: nel seguito per semplicità ci riferiremo a sistemi di forma normale. ) ìy ¢¢¢ = f (x, y, z, y ¢, z ¢, y ¢¢) í ïî z ¢¢ = g(x, y, z, y ¢, z ¢, y ¢¢)

Un’equazione d’ordine n, si scrive y (n) f (x, y, y , , y K = ¢ (n - 1) ) ed è in generale accompagnata da opportune condizioni iniziali o al contorno Mostriamo come si possa trasformare l’equazione data in un sistema equivalente di n equazioni del prim’ordine in n funzioni incognite

Facciamo le seguenti posizioni ì y 1 = y ï 2 = ï íy 3 = ï K ïîy n = y¢ K y ¢¢ K K ( n -1) y

Allora l’equazione d’ordine n equivale al sistema del prim’ordine ì y 1¢ = y 2 ï y y ï 2¢ = 3 ï y 4 íy 3¢ = ï K K ï ïîy n¢ = f (x, y 1 , y 2 , K , y n )

In generale, un sistema di n equazioni, ciascuna d’ordine m, è equivalente a un sistema di n. m equazioni del prim’ordine. Useremo la notazione Y per indicare un vettore colonna avente n componenti y 1, … , yn. In questo modo un sistema di n equazioni del prim’ordine in n funzioni incognite, in forma normale, si scrive

(1) Y ¢ = F(x, Y ) in modo simile alla notazione di una sola equazione differenziale, dove



In particolare, se si tratta di un sistema d’equazioni lineari Y ¢ = A(x) × Y + B(x) dove

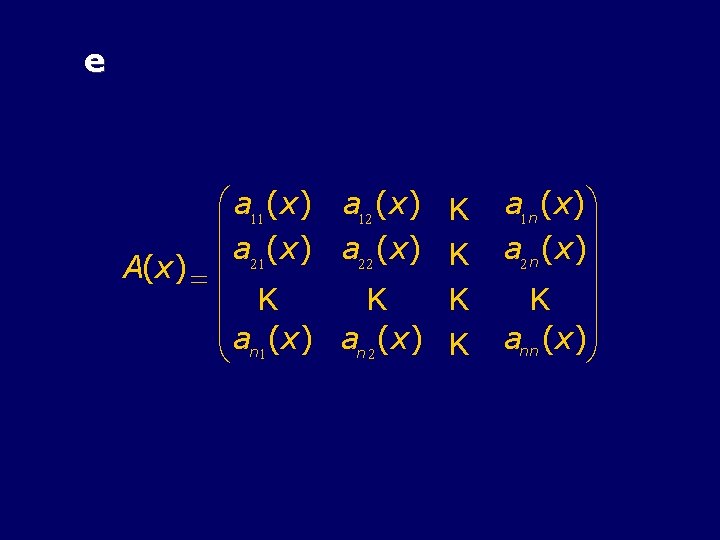
e æ a 11(x) a 12 (x) K ç a 21(x) a 22 (x) K ç A(x) = ç K K K ç ç an (x) a (x) K n 2 è 1 a 1 n(x)ö ÷ a 2 n(x)÷ K ÷ ÷ ann (x)÷ø

Qui i coefficienti bi(x) e aik(x) sono funzioni continue definite su un intervallo I (che può coincidere con tutto R) Il sistema (1) è, in generale, accompagnato da opportune condizioni iniziali; si vuole risolvere il Problema di Cauchy

(1) Y ¢ = F (x, Y ) con le condizioni iniziali (2) Y(x 0)=Y 0 Notiamo che la soluzione del pd. C (1) + (2) si presta all’ interpretazione geometrica che già abbiamo messo in evidenza nella lezione introduttiva

Se la funzione F(x, Y) è continua, allora esiste una soluzione del pd. C. Se inoltre sono continue le derivate parziali delle componenti fi rispetto alle yk allora la soluzione locale è unica.

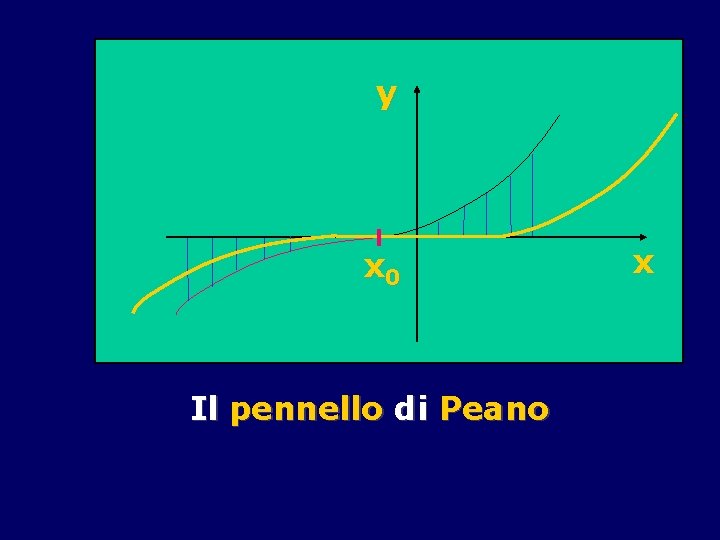
Si noti che se non sono soddisfatte le condizioni sulla continuità delle derivate parziali, la soluzione può non essere unica Esempio y’ = |y|1/2 y(x 0) = y 0 Dy |y|1/2 = 1/2 |y|-(1/2) sign (y)

Se y 0 è ≠ 0, allora la derivata parziale è continua in un intorno di y 0. Dunque la soluzione locale è unica. Ma se y 0 = 0, non c’è continuità in alcun intorno di 0. In questo caso l’unicità può mancare.

Se y 0 > 0, allora la soluzione è data da æ x - x 0 + 2 y 0 ö y(x) = ç ÷ 2 è ø per x > x 0 2

Se y 0 < 0, allora la soluzione è data da æ x - x 0 - 2 -y 0 ö y(x) = - ç ÷ 2 è ø per x < x 0 2

Ma se y 0 = 0, allora c’è una soluzione identicamente nulla, accanto alla soluzione æ x - x 0 ö y(x) = ç ÷ è 2 ø per x > x 0 2

e alla soluzione æ x - x 0 ö y(x) = -ç ÷ è 2 ø per x < x 0 2

y x 0 Il pennello di Peano x

SISTEMI D’EQUAZIONI DIFFERENZIALI ORDINARIE LINEARI A COEFFICIENTI CONTINUI

Ci occuperemo ora della soluzione del pd. C relativo al sistema (3) Y ¢ = A(x) × Y + B(x) Con le condizioni iniziali (4) 0 0 Y(x )=Y

Se le funzioni bi(x) e aik(x) sono continue e definite su un intervallo I (che può essere tutto R) allora si può dimostrare che la soluzione esiste, è definita su tutto I ed è unica.

Accanto al sistema (3), detto completo, considereremo il sistema omogeneo (5) Y ¢ = A(x) × Y nel quale B(x) 0. Le soluzioni di (3) o di (5) sono funzioni definite su I a valori in Rn, necessariamente continue con derivata prima continua. Cioè

sono funzioni di classe C 1(I, Rn). converrà considerare l’operatore differenziale associato a (3) o a (5) (6) L(Y)= Y ¢ - A(x) × Y Che a ogni funzione Y(x): I Rn associa Y’(x) - A(x) ×Y; questa è una funzione continua su I a valori in Rn. Cioè L è un’applicazione lineare da C 1(I, Rn) a C 0(I, Rn).

Le soluzioni di (5) danno dunque il nucleo di L: ker(L). Teorema ker(L) C 1(I, Rn) è un sottospazio di di dimensione n di C 1(I, Rn). Ossia ker(L) è isomorfo a Rn.

Si fissi un punto x 0 in I e sia Y(x) una soluzione di (5). Allora Y(x 0) è un vettore di Rn. Se Y 1(x) ≠ Y 2(x) allora Y 1(x 0) ≠ Y 2(x 0) per l’unicità della soluzione del pd. C (5) + (4). Se poi Y 0 è un arbitrario vettore di Rn esiste una soluzione di (5) + (4), per l’esistenza della soluzione del pd. C corrispondente. L’applicazione N : ker(L) ® R n

definita da 0) ( ( ) NY x =Y x è un isomorfismo tra ker(L) e Rn. Infatti abbiamo verificato che è biiettiva; inoltre è lineare. Ma spazi vettoriali isomorfi hanno la stessa dimensione: dim ker(L) = n. Esistono dunque n funzioni linearmente indipendenti soluzioni di L(Y) = 0: Y 1(x), Y 2(x), . . , Yn(x).

Ogni soluzione di (5) è perciò una combinazione lineare delle precedenti funzioni Y 1(x), Y 2(x), . . , Yn(x). Si noti che, date n soluzioni di (5), se esse, calcolate in un punto x 0, danno vettori lin. indipendenti di Rn, allora sono l. i. in ogni altro punto di I. Ciò è conseguenza dell’unicità della soluzione del pd. C.

Mostriamo ora che tutte le soluzioni del sistema completo (3) sono del tipo Y(x) = Z(x) + Y(x) dove Z(x) è una soluzione del sistema omogeneo e Y(x) è una Soluzione particolare di (3).

Infatti L(Y ) = L(Z) + L(Y ) = 0 + B(x) = B(x) Se poi abbiamo due soluzioni del sistema completo Y(x) e Y(x) la loro differenza soddisfa L(Y - Y ) = L(Y ) - L(Y ) = B(x) - B(x) = 0 cioè Y(x) - Y(x) = Z(x) �è una soluzione del sistema omogeneo.

Se Y 1(x), Y 2(x), . . , Yn(x) sono soluzioni l. i. del sistema omogeneo, si dice che formano un insieme (o sistema) fondamentale di soluzioni del sistema (5). La matrice U(x) le cui colonne sono date da Y 1(x), Y 2(x), . . , Yn(x) l. i. , si dice una matrice fondamentale Si noti che se det U(x 0) ≠ 0 allora det U(x) ≠ 0 per ogni x in I.

Evidentemente per la matrice fondamentale U(x) vale l’equazione U’(x) - A(x) ×U(x) = 0 La soluzione generale del sistema omogeneo L(Y) = 0, è una combinazione lineare dell’insieme fondamentale:

Y(x) = c 1 Y 1(x)+c 2 Y 2(x)+. . +cn. Yn(x) = =U(x) ×(c 1, c 2, . . , cn)T Il metodo della variazione delle costanti suggerisce di cercare per (3) una soluzione della forma Y(x) = U(x) ×Z(x)


Ossia U(x) × Z’(x) = B(x) E finalmente Z’(x) = U(x)-1 × B(x)

Integrando Z(x) = ò U (t) × B(t)dt -1 E in conclusione Y(x) = U(x) ò U (t) × B(t)dt -1

Il metodo per trovare un integrale particolare del sistema completo sarà utile anche nel caso di una singola equazione lineare completa d’ordine n.
 Sistemi di equazioni non lineari
Sistemi di equazioni non lineari Equazioni differenziali schema riassuntivo
Equazioni differenziali schema riassuntivo Gabriella puppo
Gabriella puppo Equazioni differenziali di eulero
Equazioni differenziali di eulero Equazioni differenziali applicazioni economiche
Equazioni differenziali applicazioni economiche Sistemi metodo confronto
Sistemi metodo confronto Sistemi non lineari
Sistemi non lineari Sistemi lineari tempo invarianti
Sistemi lineari tempo invarianti Sistema di disequazioni lineari
Sistema di disequazioni lineari Sistemi di equazioni e disequazioni
Sistemi di equazioni e disequazioni Trasformatore differenziale
Trasformatore differenziale Costi differenziali esempi
Costi differenziali esempi Manicotto vincolo
Manicotto vincolo Funzione
Funzione Punto di sella
Punto di sella Codici comunicativi del linguaggio logico matematico
Codici comunicativi del linguaggio logico matematico Disuguaglianze e disequazioni
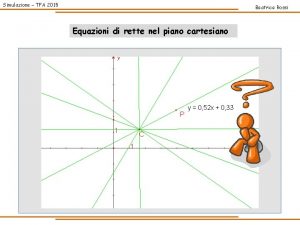
Disuguaglianze e disequazioni Dominio di una circonferenza
Dominio di una circonferenza Vulcani lineari
Vulcani lineari Indice argomenti
Indice argomenti Indice argomenti
Indice argomenti Frasi con zero argomenti
Frasi con zero argomenti Primo principio termodinamica sistemi aperti
Primo principio termodinamica sistemi aperti I moti millenari della terra zanichelli
I moti millenari della terra zanichelli Fichte tre principi
Fichte tre principi F92 disturbi misti della condotta e della sfera emozionale
F92 disturbi misti della condotta e della sfera emozionale Pei disturbo misto della condotta e della sfera emozionale
Pei disturbo misto della condotta e della sfera emozionale Soluzioni il racconto delle scienze naturali
Soluzioni il racconto delle scienze naturali Il racconto della chimica e della terra
Il racconto della chimica e della terra Culture e formati della televisione e della radio
Culture e formati della televisione e della radio La coccinella in cerca della felicità pdf
La coccinella in cerca della felicità pdf Lavorazione della seta fasi
Lavorazione della seta fasi Soluzioni il racconto delle scienze naturali
Soluzioni il racconto delle scienze naturali Ritratto della mia bambina
Ritratto della mia bambina Prove della sfericità della terra
Prove della sfericità della terra Sociologia della cultura e della comunicazione units
Sociologia della cultura e della comunicazione units Soluzioni il racconto della chimica e della terra
Soluzioni il racconto della chimica e della terra Il racconto delle scienze naturali zanichelli soluzioni
Il racconto delle scienze naturali zanichelli soluzioni Soluzioni il racconto della chimica e della terra
Soluzioni il racconto della chimica e della terra Prove sulla sfericità della terra
Prove sulla sfericità della terra Dominio di un'equazione di secondo grado
Dominio di un'equazione di secondo grado Equazione 1 e 3 quadrante
Equazione 1 e 3 quadrante Potenza ad esponente reale
Potenza ad esponente reale Equazioni di secondo grado
Equazioni di secondo grado