SemiNumerical String Matching Seminumerical String Matching n n

Semi-Numerical String Matching

Semi-numerical String Matching n n n All the methods we’ve seen so far have been based on comparisons. We propose alternative methods of computation such as: Arithmetic. Bit – operations. The fast Fourier transform.

Semi-numerical String Matching n We will survey three examples of such methods: n The Random Fingerprint method due to Karp and Rabin. Shift–And method due to Baeza-Yates and Gonnet, and its extension to agrep due to Wu and Manber. A solution to the match count problem using the fast Fourier transform due to Fischer and Paterson and an improvement due to Abrahamson. n n

Karp-Rabin fingerprint - exact match n n n Exact match problem: we want to find all the occurrences of the pattern P in the text T. The pattern P is of length n. The text T is of length m.

Karp-Rabin fingerprint - exact match n Arithmetic replaces comparisons. n An efficient randomized algorithm that makes an error with small probability. A randomized algorithm that never errors whose expected running time is efficient. n n We will consider a binary alphabet: {0, 1}.

Arithmetic replaces comparisons. n n n Strings are also numbers, H: strings → numbers. Let s be a string of length n, Definition: let Tr denote the n length substring of T starting at position r.

Arithmetic replaces comparisons. n Strings are also numbers, H: strings → numbers. T=10110101 P=0101 T=10110101 P= 0101 H(T 5) = 5 = H(P) = 5 T=10110101 P= 0101 H(T 2) = 6 ≠ H(P) = 5

Arithmetic replaces comparisons. n Theorem: There is an occurrence of P starting at position r of T if and only if H(P) = H(Tr) n Proof: Follows immediately from the unique representation of a number in base 2.

Arithmetic replaces comparisons. n We can compute H(Tr) from H(Tr-1) T=10110101 T 1 = 1 0 1 1 T 2 = 0 1 1 0

Arithmetic replaces comparisons. n A simple efficient algorithm: n Compute H(T 1). Run over T Compute H(Tr) from H(Tr-1) in constant time, and make the comparisons. n n Total running time O(m)?

Karp-Rabin n n Let’s use modular arithmetic, this will help us keep the numbers small. For some integer p The fingerprint of P is defined by Hp(P) = H(P) (mod p)

Karp-Rabin n Lemma: And during this computation no number ever exceeds 2 p.

An example P=101111 p=7 H(P) = 47 Hp(P) = 47 (mod 7) = 5

Karp-Rabin n n Intermediate numbers are also kept small. We can still compute H(Tr) from H(Tr-1). Arithmetic: Modular arithmetic:

Karp-Rabin n n Intermediate numbers are also kept small. We can still compute H(Tr) from H(Tr-1). Arithmetic: Modular arithmetic:

Karp-Rabin n How about the comparisons? Arithmetic: There is an occurrence of P starting at position r of T if and only if H(P) = H(Tr) Modular arithmetic: If there is an occurrence of P starting at position r of T then Hp(P) = Hp(Tr) There are values of p for which the converse is not true!

Karp-Rabin n Definition: If Hp(P) = Hp(Tr) but P doesn’t occur in T starting at position r, we say there is a false match between P and T at position r. If there is some position r such that there is a false match between P and T at position r, we say there is a false match between P and T.

Karp-Rabin n Our goal will be to choose a modulus p such that n p is small enough to keep computations efficient. p is large enough so that the probability of a false match is kept small. n

Prime moduli limit false matches n Definition: For a positive integer u, п(u) is the number of primes that are less than or equal to u. n Prime number theorem (without proof):

Prime moduli limit false matches n Lemma (without proof): if u ≥ 29, then the product of all the primes that are less than or equal to u is greater than 2 u. n Example: u = 29, the prime numbers less than or equal to 29 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, their product is 6, 469, 693, 230 ≥ 536, 870, 912 = 229

Prime moduli limit false matches n Corollary: If u ≥ 29 and x is any number less than or equal to 2 u, then x has fewer than п(u) distinct prime divisors. n Proof: Assume x has k ≥ п(u) distinct prime divisors q 1 , …, qk then 2 u ≥ x ≥ q 1* …* qk but q 1* …* qk is at least as large as the product of the first п(u) prime numbers.

Prime moduli limit false matches n Theorem: Let I be a positive integer, and p a randomly chosen prime less than or equal to I. If nm ≥ 29 then The probability of a false match between P and T is less than or equal to п(nm) / п(I).

Prime moduli limit false matches n n n Proof: Let R be the set of positions in T where P doesn’t begin. We have By the corollary the product has at most п(nm) distinct prime divisors. If there is a false match at position r then p divides thus also divides p must be in a set of size п(nm) but p was chosen randomly out of a set of size п(I).

Random fingerprint algorithm n Choose a positive integer I. Pick a random prime p less than or equal to I, and compute P’s fingerprint – Hp(P). For each position r in T, comput Hp(Tr) and test to see if it equals Hp(P). If the numbers are equal either declare a probable match or check and declare a definite match. n Running time: excluding verification O(m). n n

How to choose I n n n The smaller I is, computations are more efficient The larger I is, the probability of a false match decresses. Proposition: When I = nm 2 1. The largest number used in the algorithm requires at most 4(log(n)+log(m)) bits. 2. The probability of a false match is at most 2. 53/m.

How to choose I n Proof:

Extensions n An idea: why not choose k primes? n Proposition: when k primes are chosen randomly and independently between 1 and I, the probability of a false match is at most n n Proof: We saw that if p allows and error it is in a set of at most п(nm) integers. A false match can occur only if each of the independently chosen k primes is in a set of size of at most п(nm) integers.

An illustaration n k = 4, n = 250, m = 4000 I = 250*40002 < 232

Even lower limits on the error n When k primes are used, the probability of a false match is at most n Proof: Suppose a false match occurs at position r. That means that each of the primes must divide |H(P)-H(Tr) | ≤ 2 n. There at most п(n) primes that divide it. Each prime is chosen from a set of size п(I) and by chance is a part of a set of size п(n).

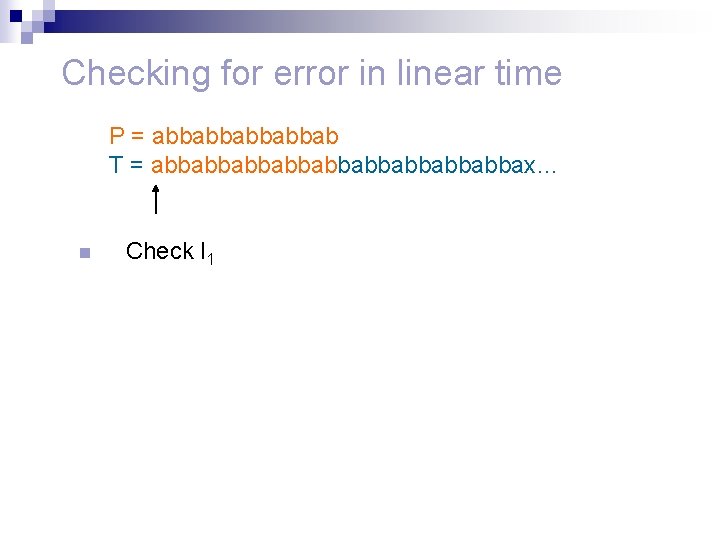
Checking for error in linear time n n n Consider the list L of locations in T where the Karp. Rabin algorithm declares P to be found. A run is a maximal interval of starting locations l 1, l 2, …, lr in L such that every two numbers differ by at most n/2. Let’s verify a run.

Checking for error in linear time n Check the first two declared occurrences explicitly. P = abbabbab T = abbabbabbabbabbax… P= abbabbab T = abbabbabbabbabbax… n n If there is a false match stop. Otherwise P is semi periodic with period d = l 1 – l 2.

Checking for error in linear time n d is the minimal period. n P = abbabbab T = abbabbabbabbabbax… P= abbabbab T = abbabbabbabbabbax…

Checking for error in linear time P = abbabbab T = abbabbabbabbabbax… n n For each i check that li+1 – li = d. Check the last d characters of li for each i.

Checking for error in linear time P = abbabbab T = abbabbabbabbabbax… n Check l 1

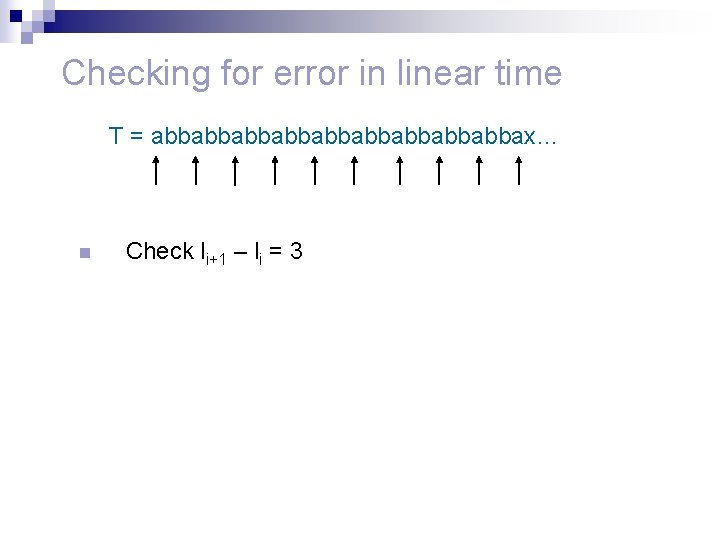
Checking for error in linear time P= abbabbab T = abbabbabbabbabbax… n Check l 2 n P is semi periodic with period 3.

Checking for error in linear time T = abbabbabbabbabbax… n Check li+1 – li = 3

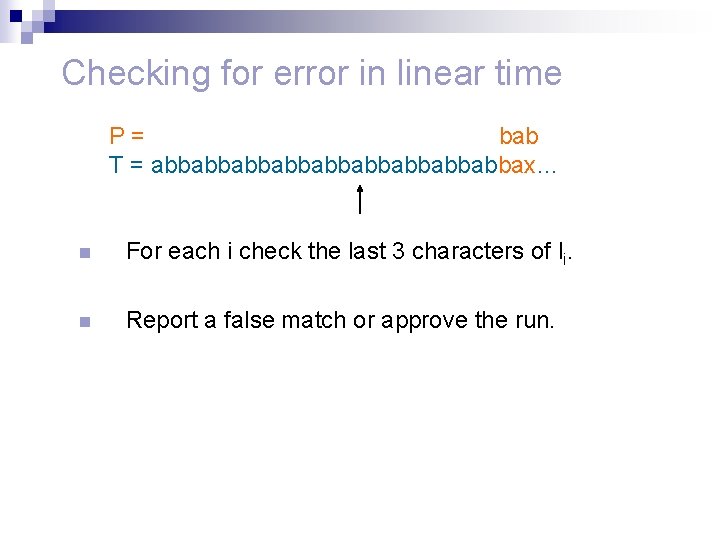
Checking for error in linear time P= bab T = abbabbabbabbabbax… n For each i check the last 3 characters of li.

Checking for error in linear time P= bab T = abbabbabbabbabbax… n For each i check the last 3 characters of li.

Checking for error in linear time P= bab T = abbabbabbabbabbax… n For each i check the last 3 characters of li. n Report a false match or approve the run.

Time analysis n n n No character of T is examined more than twice during a single run. Two runs are separated by at least n/2 positions and each run is at least n positions long. Thus no character of T is examined in more than two consecutive runs. Total verification time O(m).

Time analysis n n n When we have a false match we start again with a different prime. The expected probability of a false match is O(1/m). We have converted the algorithm to one that never mistakes with expected linear running time.

Why use Karp-Rabin? n n It is efficient and simple. It is space efficient. It can be generalized to solve harder problems such as 2 -dimensional string matching. It’s performance is backed up by a concrete theoretical analysis.

The Shift-And Method

The Shift-And Method n We start with the exact match problem. n Define M to be a binary n by m matrix such that: M(i, j) = 1 iff the first i characters of P exactly match the i characters of T ending at character j. M(i, j) = 1 iff P[1. . i] ≡ T[j-i+1. . j]

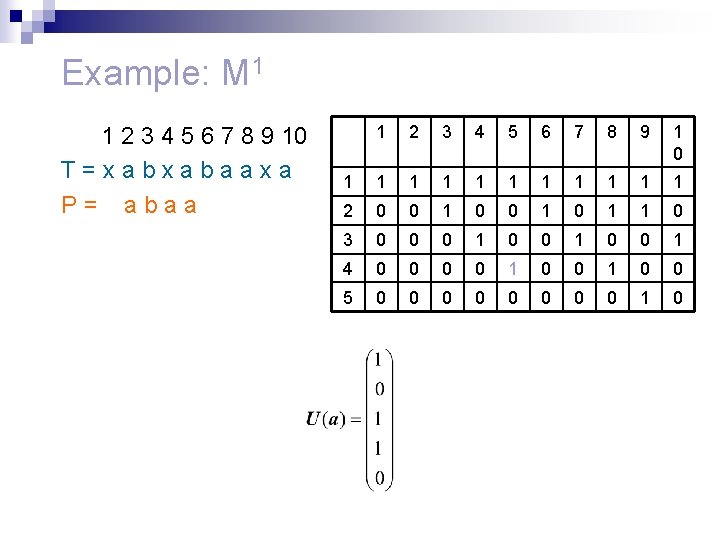
The Shift-And Method n n Let T = california Let P = for M= n n 1 2 3 4 5 6 7 8 9 m = 10 1 0 0 0 0 0 2 0 0 0 1 0 0 n=3 0 0 0 1 0 0 0 M(i, j) = 1 iff the first i characters of P exactly match the i characters of T ending at character j. How does M solve the exact match problem?

How to construct M n n We will construct M column by column. Two definitions are in order: Bit-Shift(j-1) is the vector derived by shifting the vector for column j-1 down by one and setting the first bit to 1. Example:

How to construct M n n We define the n-length binary vector U(x) for each character x in the alphabet. U(x) is set to 1 for the positions in P where character x appears. Example: P = abaac

How to construct M n n Initialize column 0 of M to all zeros For j > 1 column j is obtained by

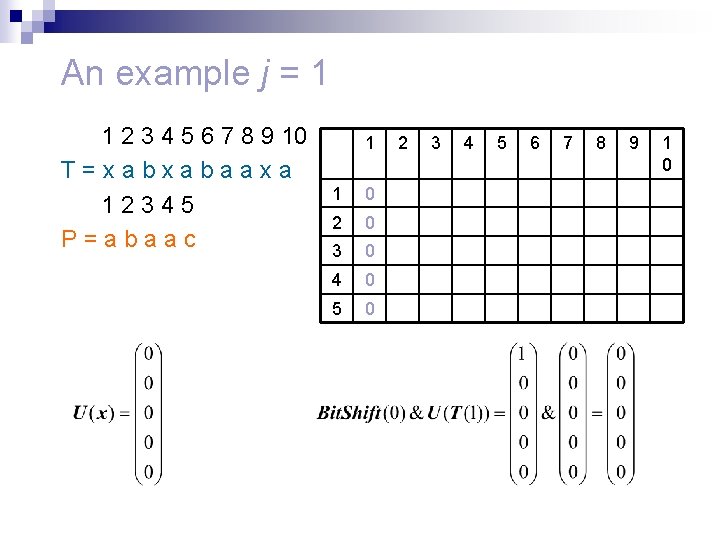
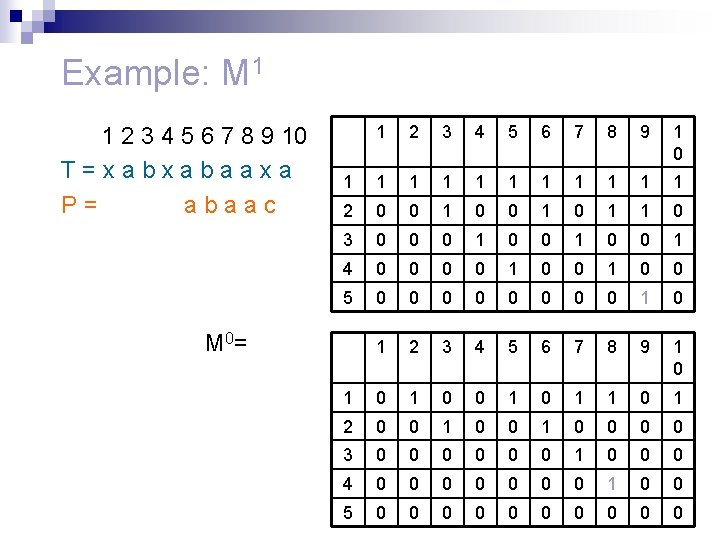
An example j = 1 1 2 3 4 5 6 7 8 9 10 T=xabxabaaxa 12345 P=abaac 1 1 0 2 0 3 0 4 0 5 0 2 3 4 5 6 7 8 9 1 0

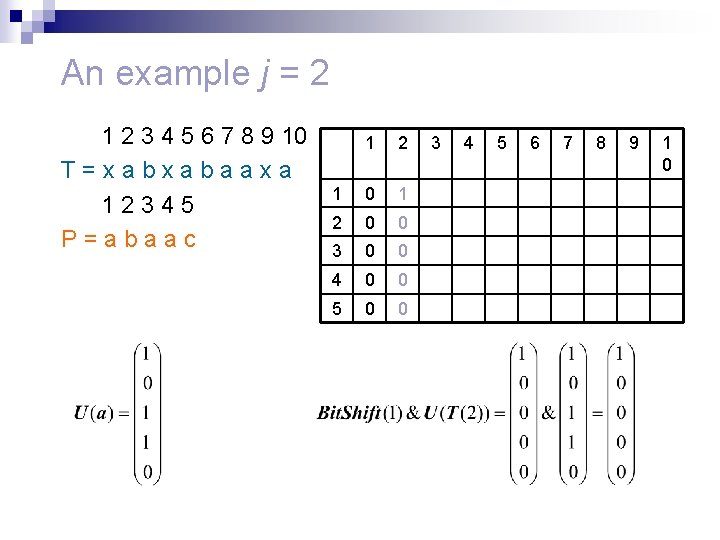
An example j = 2 1 2 3 4 5 6 7 8 9 10 T=xabxabaaxa 12345 P=abaac 1 2 1 0 1 2 0 0 3 0 0 4 0 0 5 0 0 3 4 5 6 7 8 9 1 0

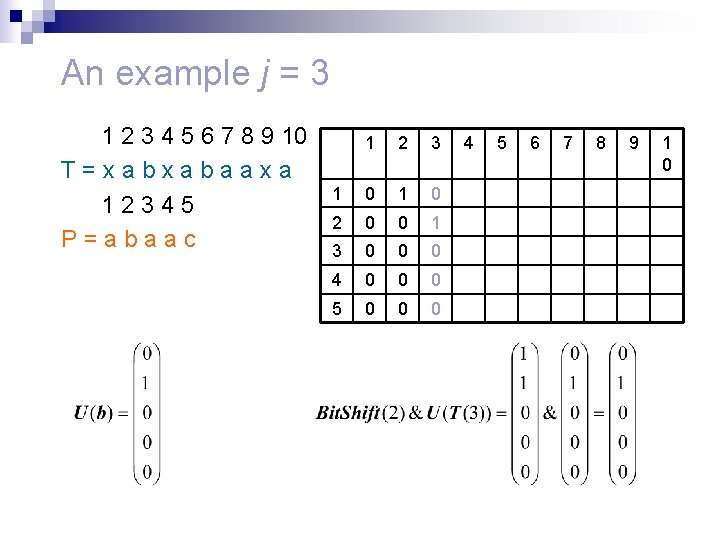
An example j = 3 1 2 3 4 5 6 7 8 9 10 T=xabxabaaxa 12345 P=abaac 1 2 3 1 0 2 0 0 1 3 0 0 0 4 0 0 0 5 0 0 0 4 5 6 7 8 9 1 0

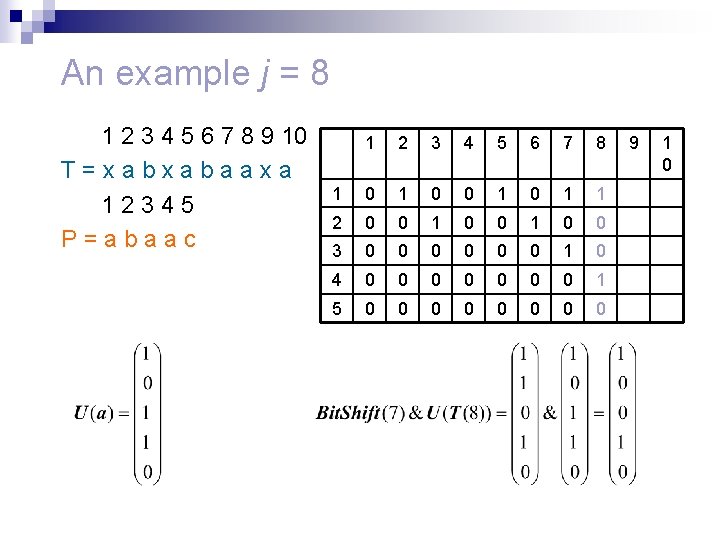
An example j = 8 1 2 3 4 5 6 7 8 9 10 T=xabxabaaxa 12345 P=abaac 1 2 3 4 5 6 7 8 1 0 0 1 1 2 0 0 1 0 0 3 0 0 0 1 0 4 0 0 0 0 1 5 0 0 0 0 9 1 0

Correctness n 1) 2) For i > 1, Entry M(i, j) = 1 iff The first i-1 characters of P match the i-1 characters of T ending at character j-1. Character P(i) ≡ T(j). n 1) is true when M(i-1, j-1) = 1. 2) is true when the i’th bit of U(T(j)) = 1. n The algorithm computes the and of these two bits. n

Correctness 1 2 3 4 5 6 7 8 9 10 T=xabxabaaxa abaac n n n 1 2 3 4 5 6 7 8 9 1 0 1 0 0 1 1 0 1 2 0 0 1 0 0 3 0 0 0 1 0 0 0 4 0 0 0 0 1 0 0 5 0 0 0 0 0 M(4, 8) = 1, this is because a b a a is a prefix of P of length 4 that ends at position 8 in T. Condition 1) – We had a b a as a prefix of length 3 that ended at position 7 in T ↔ M(3, 7) = 1. Condition 2) – The fourth bit of P is the eighth bit of T ↔ The fourth bit of U(T(8)) = 1.

How much did we pay? n n n Formally the running time is Θ(mn). However, the method is very efficient if n is the size of a single or a few computer words. Furthermore only two columns of M are needed at any given time. Hence, the space used by the algorithm is O(n).

agrep: The Shift-And Method with errors n We extend the shift-and method for finding inexact occurrences of a pattern in a text. n Reminder example: T = aatatccacaa P = atcgaa P appears in T with 2 mismatches starting at position 4, it also occurs with 4 mismatches starting at position 2. aatatccacaa atcgaa

agrep n Our current goal given k find all the occurrences of P in T with up to k mismatches. n We define the matrix Mk to be an n by m binary matrix, such that: Mk (i, j) = 1 iff At least i-k of the first i characters of P match the i characters up through character j of T. n n What is M 0? How does Mk solve the k-mismatch problem?

Computing Mk n n We compute Ml for all l=0, … , k. For each j compute M(j), M 1(j), … , Mk(j) For all l initialize Ml(0) to the zero vector. The j’th column of Ml is given by:

Computing Mk n The first i-1 characters of P match a substring of T ending at j-1, with at most l mismatches, and the next pair of characters in P and T are equal. j-1 * * * * * i-1 n

Computing Mk n The first i-1 characters of P match a substring of T ending at j-1, with at most l -1 mismatches. j-1 * * * * * i-1 n

Computing Mk n n We compute Ml for all l=1, … , k. For each j compute M(j), M 1(j), … , Mk(j) For all l initialize Ml(0) to the zero vector. The j’th column of Ml is given by:

Example: M 1 1 2 3 4 5 6 7 8 9 10 T=xabxabaaxa P= abaac 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 0 0 1 0 1 1 0 3 0 0 0 1 4 0 0 1 0 0 5 0 0 0 0 1 0 1 2 3 4 5 6 7 8 9 1 0 1 0 0 1 1 0 1 2 0 0 1 0 0 3 0 0 0 1 0 0 0 4 0 0 0 0 1 0 0 5 0 0 0 0 0 M 0 =

Example: M 1 1 2 3 4 5 6 7 8 9 10 T=xabxabaaxa P= abaa 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 0 0 1 0 1 1 0 3 0 0 0 1 4 0 0 1 0 0 5 0 0 0 0 1 0

How much did we pay? n n n Formally the running time is Θ(kmn). Again, the method is practically efficient for small n. Still only a constant number of columns of M are needed at any given time. Hence, the space used by the algorithm is O(n).

The match count problem

The match-count problem n We want to count the exact number of characters that match each of the different alignments of P with T. aatatccacaa atcgaa 4 aatatccacaa atcgaa 2

The match-count problem n n n We will first look at a simple algorithm which extends the techniques we’ve seen so far. Next, we introduce a more efficient algorithm that exploits existing efficient methods to calculate the Fourier transform. We conclude with a variation that gives good performance for unbounded alphabets.

Match-count Algorithm 1 n We define the matrix MC to be an n by m integer valued matrix, such that: MC(i, j) = The number of characters of P[1. . i] that match T[j. I+1, . . , j] n How does MC solve the match-count problem?

Computing MC n Initialize column 0 of MC to all zeros For j ≥ 1 column j is obtained by n Total of Θ(nm) comparisons and (simple) additions. n

Match-count algorithm 2 n Define a vector W that counts the matching symbols, it’s indices are the possible alignments. T=ababcaaa P=abca W(1) = 2 ababcaaa abca W(3) = 4 ababcaaa abca W(5) = 1 ababcaaa abca W(2) = 0 ababcaaa abca W(4) = 1

Match-count algorithm 2 n Let’s handle one symbol at a time: T=ababcaaa P=abca Ta = 1 0 0 1 1 1 Pa = 1 0 0 1 Wa(1) = 1 10100111 1001 Wa(3) = 2

Match-count algorithm 2 n We have W = Wa + Wb + Wc. n Or in the general case n

Match-count algorithm 2 n We can calculate Wα using a convolution. n n Let’s rephrase the problem. X = Tα padded with n zeros on the right. Y = Pα padded with m zeros on the right. n We have two vectors X, Y of length m+n. n

Match-count algorithm 2 n Ta = 1 0 0 1 1 1 Pa = 1 0 0 1 X=101001110000 Y=10010000

Match-count algorithm 2 n In our modified representation: n Where the indices are taken modulo n+m. W(1) = W(2) = < 1 0 0 1 1 1 0 0, 10010000 > <010100111000, 010010000000 >

Match-count algorithm 2 n In our modified representation: n Where the indices are taken modulo n+m. n This is the convolution of X and the reverse of Y. n Using FFT calculating convolution takes time O(m log(m)).

Match-count algorithm 2 n The total running time is O(|∑| m log(m)) n What happens if |∑| is large? n For example when |∑| =n, we get O(n m log(m)) which is actually worse than the naïve algorithm.

Match-count algorithm 3 n n n An idea: some symbols might appear more often than others. Use convolutions for the frequent symbols. Use a more simple counting method for the rest.

Rare symbols n n n Say α appears less than c times in P. Record the locations of α in P l 1, …, lr r ≤c. Go over the text, when we see α at location j we increment W(j-l 1+1) , … , W(j-lr+1+1).

Rare symbols T = a b c a a a… P=abcac l 1 = 3, l 2 = 5 j = 5 → W(5 -3+1)++ W(3)++ a b c a a a… abcac W(5 -5+1)++ W(1)++ T = a b c a a a. . . abcac

How much did we pay? n n n We can do this for all the rare symbols in one sweep of T, for each position in T we make up to c updates in W. Thus handling the rare symbols will cost us O(cm). For the frequent symbols we pay one convolution per symbol so we pay at most O(n/c m log(m)).

Determining c n We choose the c that gives us the best balance n The total running time is

References n Dan Gusfield, Algorithms on Strings, Trees and Graphs. Cambridge Univ. Press, Cambridge, 1997.

The end