Pattern Matching in String Pattern Matching in String

Pattern Matching in String

Pattern Matching in String Bài toán: Cho: Tập các kí tự xâu kí tự P (pattern), |P| = m, văn bản T, |T| = n, n>>m. Câu hỏi: P T? Nếu P T: vị trí xuất hiện đầu tiên của P trong T? 2020 -10 -02 Dao Thanh Tinh Example 1: P = ABABDE ║║║║║║ T = ABABABDEAA, i 0=3 2

A Straightforward String Matching Brute Force Algorithm Input: Output: P[1. . m], T[1. . n]; i 0 (if P T[i 0. . i 0+m-1], i 0 1, otherwise i 0=0) a) i=1; j= i; k=1; b) while (j n) & (k m) if (T(j) = P(k)) { j++; k++; } else { i++; j=i; k=1; } c) if (k>m) i 0 : = i else i 0 : =0; Cpmplexity: O(mn). 2020 -10 -02 Dao Thanh Tinh 3

A Straightforward String Matching Brute Force Algorithm (*) Input: Output: P[1. . m], T[1. . n]; i 0 (if P T[i 0. . i 0+m-1], i 0 1, otherwise i 0=0) a) j= 1; k=1; b) while (j n) & (k m) if (T(j) = P(k)) { j++; k++; } else {j = j k+2; k=1; } c) if (k>m) i 0 : = j m else i 0 : =0; 1 2 3 4 5 P T A B E j A A A B B D E A A 1 2 3 4 5 6 7 8 9 10 11 12 k=5, j=7 On the new step: k=1, j= 7 – 5 + 2 = 4 k 1 2 3 4 5 P T A B E j Cpmplexity: O(mn). 2020 -10 -02 k Dao Thanh Tinh A A A B B D E A A 1 2 3 4 5 6 7 8 9 10 11 4 12

A Straightforward String Matching Example 2: P = ABABDE T = ABABABDEAA Example 3: P = UUUUUUX T = UUUUUU P = ABABDE ║║║║ T = ABABABDEAA P = UUUUUUX ║║║║║║ T = UUUUUU P = ABABDE ║║║║ T = A BABABDEAA P = UUUUUUX ║║║║║║ T = UUUUUU P = ABABDE ║║║║║║ T = ABABABDEAA, successful match, i 0=3 2020 -10 -02 Dao Thanh Tinh 5

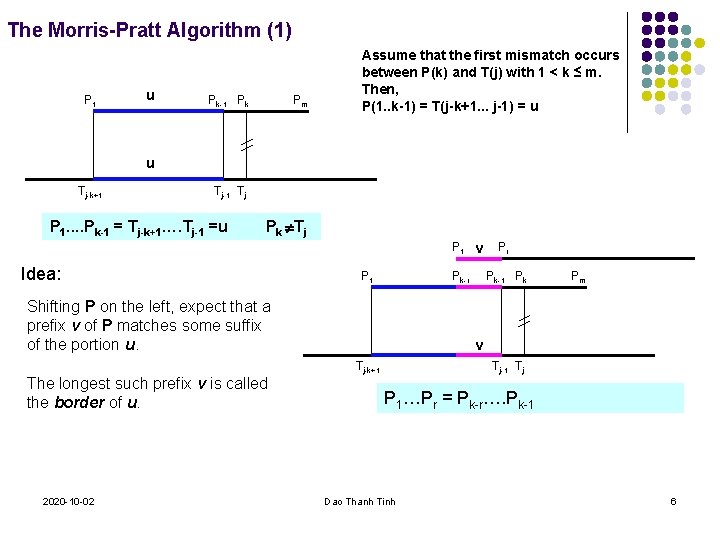
The Morris-Pratt Algorithm (1) P 1 u Pk-1 Pk Pm Assume that the first mismatch occurs between P(k) and T(j) with 1 < k ≤ m. Then, P(1. . k-1) = T(j-k+1. . . j-1) = u u Tj-k+1 Tj-1 Tj P 1. . Pk-1 = Tj-k+1…. Tj-1 =u Pk Tj P 1 v Idea: P 1 Pk-r Shifting P on the left, expect that a prefix v of P matches some suffix of the portion u. The longest such prefix v is called the border of u. 2020 -10 -02 Pr Pk-1 Pk Pm v Tj-1 Tj Tj-k+1 P 1…Pr = Pk-r…. Pk-1 Dao Thanh Tinh 6

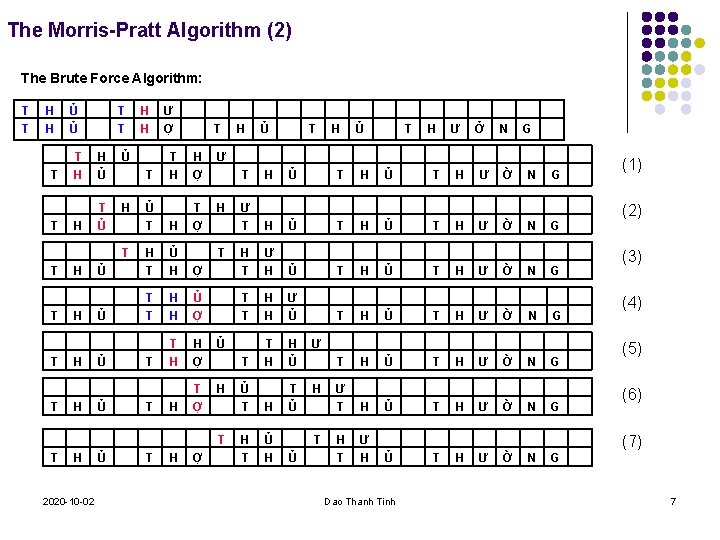
The Morris-Pratt Algorithm (2) The Brute Force Algorithm: T T H H T T Ủ Ủ T T T H H Ủ Ủ H H T Ủ T T T H H Ư Ợ T T H H Ợ Ư Ủ T H H T Ợ Ủ H T Ủ H Ủ T T T H H Ủ Ủ T H 2020 -10 -02 Ủ T H Ư Ở N G T H Ủ T H Ư Ờ N G Ư T H Ủ T H Ư Ờ N G Ợ H T Ư H Ủ T H Ư Ờ N G H H Ủ Ợ T T H H Ư Ủ T H Ư Ờ N G T H H Ợ Ủ H Ủ Ư T T H Ủ T H Ư Ờ N G H Ủ T H T Ủ H H T Ợ Ư T H Ủ T H Ư Ờ N G H T Ủ H H T Ư H T T T H H Ợ T Ủ (1) (2) (3) (4) (5) (6) (7) Ủ Dao Thanh Tinh T H Ư Ờ N G 7

The Morris-Pratt Algorithm (3) (8) T H Ủ T H Ợ T T H H Ủ Ủ T T H H H T Ủ (9) T H Ủ T H Ợ (10) (11) T H Ủ T H Ợ T T T H H Ư Ủ H Ủ Ư T T H Ủ T H H T Ủ Ủ H T Ủ H Ủ T T H H T (12) T H Ủ T H Ợ T H (13) T H Ủ T H Ợ T H Ư Ờ N G Ư T H Ư Ờ N G Ủ H T Ư H Ư Ờ N G Ủ Ủ T T H H Ư Ư Ờ N G T The Brute Force Algorithm performs on 13 steps. 2020 -10 -02 Dao Thanh Tinh 8

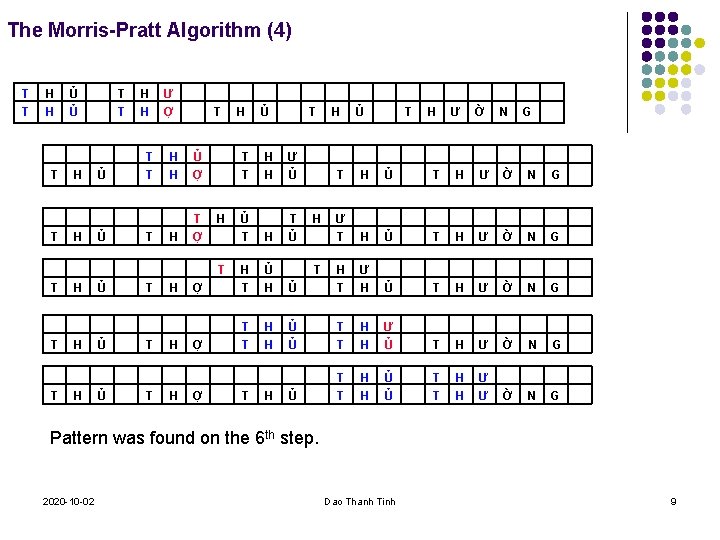
The Morris-Pratt Algorithm (4) T T H H T T Ủ Ủ H H T T T Ư Ợ T H H Ủ Ợ H T Ợ T T H H H Ủ Ủ Ủ T T T H H H Ủ T H H Ư Ủ Ủ T H T Ủ Ợ H T Ủ H Ợ T T H H H T T H Ợ T H H Ủ T H Ư Ờ N G T H Ủ T H Ư Ờ N G Ư T H Ủ T H Ư Ờ N G Ủ H T Ư H Ủ T H Ư Ờ N G Ủ Ủ T T H H Ư Ủ T H Ư Ờ N G Ủ T T H H Ủ Ủ T T H H Ư Ư Ờ N G H T Pattern was found on the 6 th step. 2020 -10 -02 Dao Thanh Tinh 9

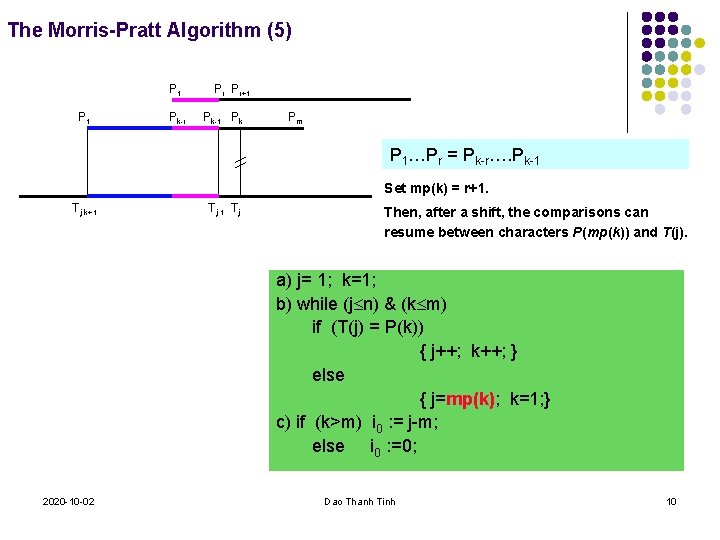
The Morris-Pratt Algorithm (5) P 1 Pk-r Pr Pr+1 Pk-1 Pk Pm P 1…Pr = Pk-r…. Pk-1 Set mp(k) = r+1. Tj-k+1 Tj-1 Tj Then, after a shift, the comparisons can resume between characters P(mp(k)) and T(j). a) j= 1; k=1; b) while (j n) & (k m) if (T(j) = P(k)) { j++; k++; } else { j=mp(k); k=1; } c) if (k>m) i 0 : = j-m; else i 0 : =0; 2020 -10 -02 Dao Thanh Tinh 10

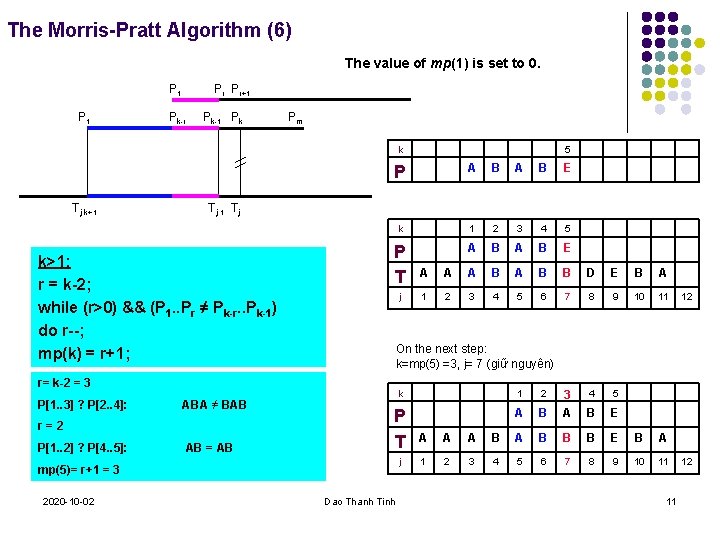
The Morris-Pratt Algorithm (6) The value of mp(1) is set to 0. Pr Pr+1 P 1 Pk-r Pk-1 Pk Pm k Tj-k+1 P A B E k 1 2 3 4 5 P T A B E Tj-1 Tj k>1: r = k-2; while (r>0) && (P 1. . Pr ≠ Pk-r. . Pk-1) do r--; mp(k) = r+1; j ABA ≠ BAB r=2 P[1. . 2] ? P[4. . 5]: AB = AB A A B B D E B A 1 2 3 4 5 6 7 8 9 10 11 4 5 B E k 1 2 P T A B 3 A j mp(5)= r+1 = 3 2020 -10 -02 A 12 On the next step: k=mp(5) =3, j= 7 (giữ nguyên) r= k-2 = 3 P[1. . 3] ? P[2. . 4]: 5 Dao Thanh Tinh A A A B B B E B A 1 2 3 4 5 6 7 8 9 10 11 11 12

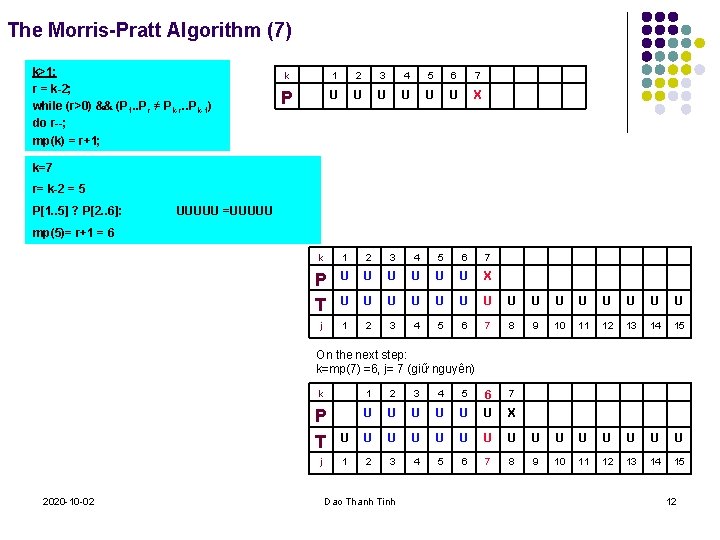
The Morris-Pratt Algorithm (7) k>1: r = k-2; while (r>0) && (P 1. . Pr ≠ Pk-r. . Pk-1) do r--; mp(k) = r+1; k 1 2 3 4 5 6 7 P U U U X k=7 r= k-2 = 5 P[1. . 5] ? P[2. . 6]: UUUUU =UUUUU mp(5)= r+1 = 6 k 1 2 3 4 5 6 7 P T U U U X U U U U j 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 7 X On the next step: k=mp(7) =6, j= 7 (giữ nguyên) k 1 2 3 4 5 P T U U U 6 U U U U 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 j 2020 -10 -02 Dao Thanh Tinh 12

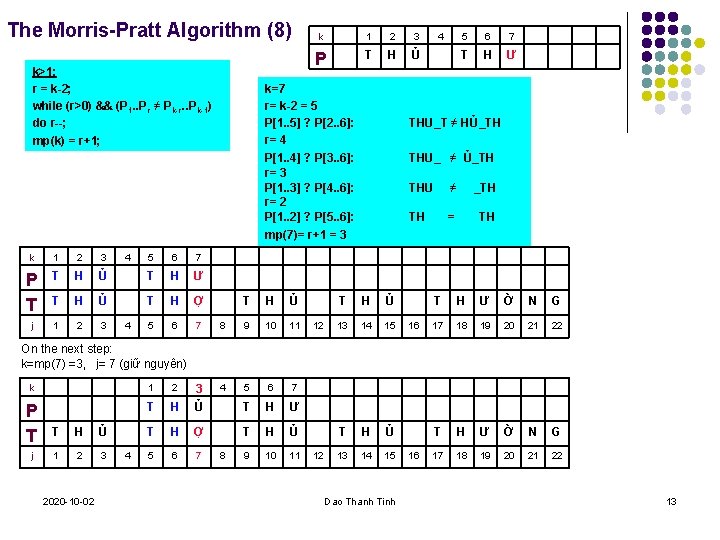
The Morris-Pratt Algorithm (8) k>1: r = k-2; while (r>0) && (P 1. . Pr ≠ Pk-r. . Pk-1) do r--; mp(k) = r+1; k 1 2 3 P T H Ủ k=7 r= k-2 = 5 P[1. . 5] ? P[2. . 6]: r= 4 P[1. . 4] ? P[3. . 6]: r= 3 P[1. . 3] ? P[4. . 6]: r= 2 P[1. . 2] ? P[5. . 6]: 4 5 6 7 T H Ư THU_T ≠ HỦ_TH THU_ ≠ Ủ_TH THU ≠ _TH TH = TH mp(7)= r+1 = 3 k 1 2 3 P T T H T j 1 4 5 6 7 Ủ T H Ư H Ủ T H Ợ 2 3 5 6 7 4 T H Ủ 8 9 10 11 4 5 6 7 T H Ư T H Ủ 9 10 11 12 T H Ủ 13 14 15 16 T H Ư Ờ N G 17 18 19 20 21 22 On the next step: k=mp(7) =3, j= 7 (giữ nguyên) k 1 2 P T T H 3 Ủ T H Ợ 5 6 7 j T H Ủ 1 2 3 2020 -10 -02 4 8 12 Dao Thanh Tinh 16 13

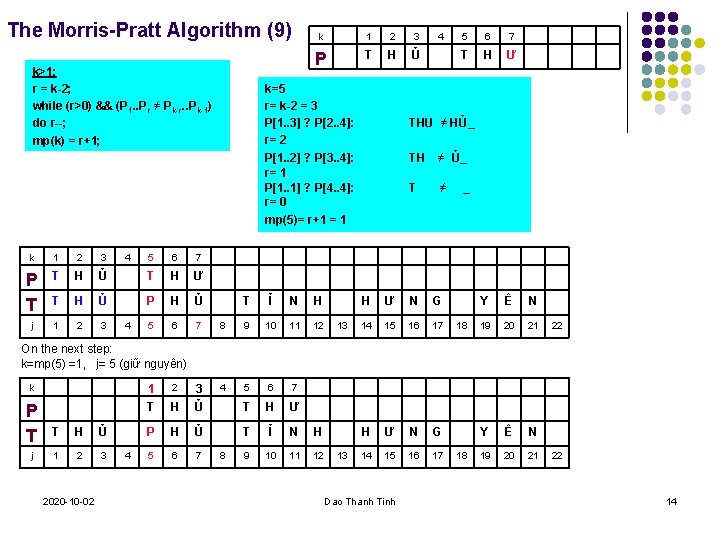
The Morris-Pratt Algorithm (9) k>1: r = k-2; while (r>0) && (P 1. . Pr ≠ Pk-r. . Pk-1) do r--; mp(k) = r+1; k 1 2 3 P T H Ủ k=5 r= k-2 = 3 P[1. . 3] ? P[2. . 4]: r= 2 P[1. . 2] ? P[3. . 4]: r= 1 P[1. . 1] ? P[4. . 4]: r= 0 4 5 6 7 T H Ư Y Ê N 19 20 21 THU ≠ HỦ_ TH ≠ Ủ_ T ≠ _ mp(5)= r+1 = 1 k 1 2 3 P T T H T j 1 4 5 6 7 Ủ T H Ư H Ủ P H Ủ 2 3 5 6 7 4 T Ỉ N H 8 9 10 11 12 4 5 6 7 T H Ư T Ỉ N H 9 10 11 12 13 H Ư N G 14 15 16 17 18 22 On the next step: k=mp(5) =1, j= 5 (giữ nguyên) k P T j T H Ủ 1 2 3 2020 -10 -02 4 2 1 T H 3 Ủ P H Ủ 5 6 7 8 13 Dao Thanh Tinh 18 22 14

The Morris-Pratt Algorithm (10) P 1 k=1: r = -1 mp(k) = 0 ? Pm Tj Tj+1 k=1: mp(1) = 0 comparisons can resume between characters P(mp(k)) = P(0) and T(j), but P(0) is not existent. In this case, comparisons can resume between P(1) and T(j+1). Then, set mp(1) = 1, j= j+1. 2020 -10 -02 Dao Thanh Tinh 15

The Morris-Pratt Algorithm (11) k=2. . m: r = k-2; while (r>0) && (P 1. . Pr ≠ Pk-r. . Pk-1) do r--; mp(k) = r+1; k=1: mp(k)=1. mp k =7 T H Ủ T H Ư 3 6 T H Ủ T H Ư 2 5 T H Ủ T H Ư 1 4 T H Ủ T H Ư 1 3 T H Ủ T H Ư 1 2 T H Ủ T H Ư 1 1 T H Ủ T H Ư 1 2020 -10 -02 a) j= 1; k=1; b) while (j n) & (k m) if (T(j) = P(k)) { j++; k++; } else { if (k=1) j++; k=mp(k); } c) if (k>m) i 0 : = j-m; else i 0 : =0; Dao Thanh Tinh 16

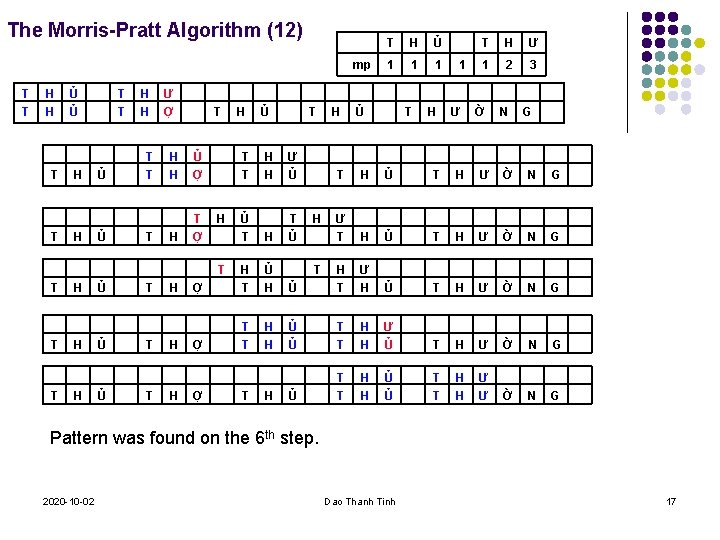
The Morris-Pratt Algorithm (12) mp T T H H T T Ủ Ủ H H T T T Ư Ợ T H H Ủ Ợ H T Ợ T T H H H Ủ Ủ Ủ T T T H H H Ủ T H H Ư Ủ Ủ T H T Ủ Ợ H T Ủ H Ợ T T H H H T T H Ợ T H H T H Ủ 1 1 1 Ủ T H 1 Ư T H Ư 1 2 3 Ờ N G T H Ủ T H Ư Ờ N G Ư T H Ủ T H Ư Ờ N G Ủ H T Ư H Ủ T H Ư Ờ N G Ủ Ủ T T H H Ư Ủ T H Ư Ờ N G Ủ T T H H Ủ Ủ T T H H Ư Ư Ờ N G H T Pattern was found on the 6 th step. 2020 -10 -02 Dao Thanh Tinh 17

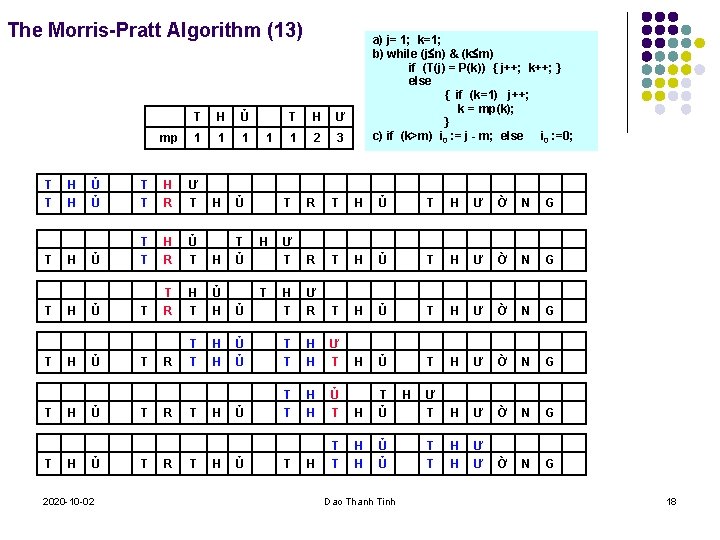
The Morris-Pratt Algorithm (13) mp T T T T H H H H T H Ủ 1 1 1 H Ủ T Ủ Ủ Ủ T T H R Ư T Ủ T T H R Ủ T H T T R H T Ủ H R T T H H Ủ Ủ 2020 -10 -02 T T T R R T T H H 1 T H Ư 1 2 3 a) j= 1; k=1; b) while (j n) & (k m) if (T(j) = P(k)) { j++; k++; } else { if (k=1) j++; k = mp(k); } c) if (k>m) i 0 : = j - m; else i 0 : =0; T R T H Ủ T H Ư Ờ N G Ư T R T H Ủ T H Ư Ờ N G Ủ H T Ư R T H Ủ T H Ư Ờ N G Ủ Ủ T T H H Ư T H Ủ T H Ư Ờ N G Ủ T T H H Ủ T H T Ủ Ư T H Ư Ờ N G H T T H H Ủ Ủ T T H H Ư Ư Ờ N G H T Ủ T Dao Thanh Tinh H 18

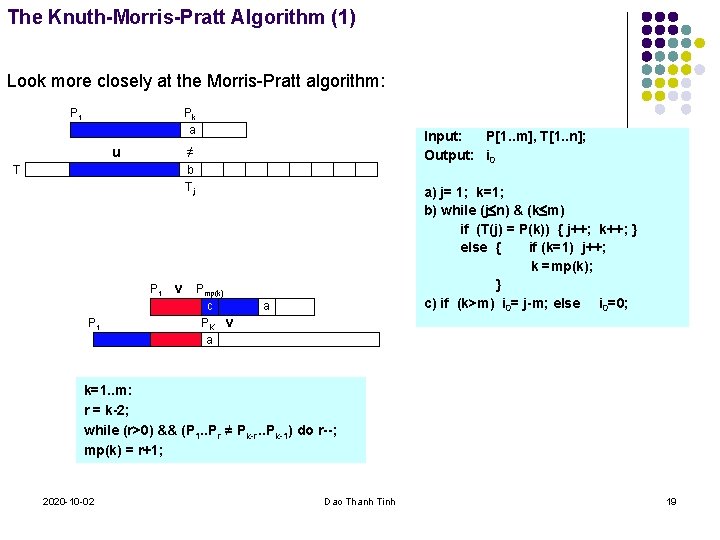
The Knuth-Morris-Pratt Algorithm (1) Look more closely at the Morris-Pratt algorithm: P 1 Pk a u Input: P[1. . m], T[1. . n]; Output: i 0 ≠ T b Tj P 1 v P 1 Pmp(k) c PK v a a) j= 1; k=1; b) while (j n) & (k m) if (T(j) = P(k)) { j++; k++; } else { if (k=1) j++; k =mp(k); } c) if (k>m) i 0= j-m; else i 0=0; a k=1. . m: r = k-2; while (r>0) && (P 1. . Pr ≠ Pk-r. . Pk-1) do r--; mp(k) = r+1; 2020 -10 -02 Dao Thanh Tinh 19

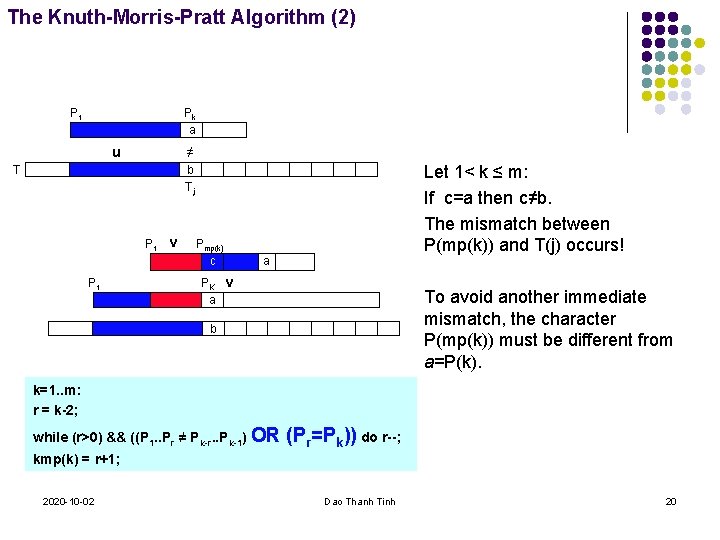
The Knuth-Morris-Pratt Algorithm (2) P 1 Pk a u ≠ T Let 1< k ≤ m: If c=a then c≠b. The mismatch between P(mp(k)) and T(j) occurs! b Tj P 1 v P 1 Pmp(k) c a PK v a To avoid another immediate mismatch, the character P(mp(k)) must be different from a=P(k). b k=1. . m: r = k-2; while (r>0) && ((P 1. . Pr ≠ Pk-r. . Pk-1) OR (Pr=Pk)) do r--; kmp(k) = r+1; 2020 -10 -02 Dao Thanh Tinh 20

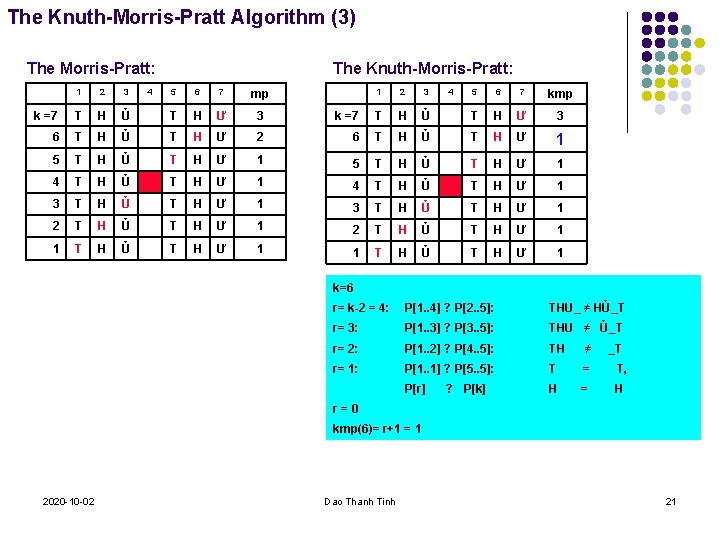
The Knuth-Morris-Pratt Algorithm (3) The Morris-Pratt: The Knuth-Morris-Pratt: 1 2 3 k =7 T H 2 6 T Ư 1 5 H Ư 1 T H Ư Ủ T H 1 2 3 k =7 T H 6 T 5 4 5 6 7 kmp Ủ T H Ư 3 H Ủ T H Ư 1 T H Ủ T H Ư 1 4 T H Ủ T H Ư 1 1 3 T H Ủ T H Ư 1 2 T H Ủ T H Ư 1 1 T H Ủ T H Ư 1 5 6 7 mp Ủ T H Ư 3 H Ủ T H Ư T H Ủ T H 4 T H Ủ T 3 T H Ủ 2 T H 1 T H 4 k=6 r= k-2 = 4: P[1. . 4] ? P[2. . 5]: THU_ ≠ HỦ_T r= 3: P[1. . 3] ? P[3. . 5]: THU ≠ Ủ_T r= 2: P[1. . 2] ? P[4. . 5]: TH ≠ r= 1: P[1. . 1] ? P[5. . 5]: T = T, P[r] H = H ? P[k] _T r=0 kmp(6)= r+1 = 1 2020 -10 -02 Dao Thanh Tinh 21

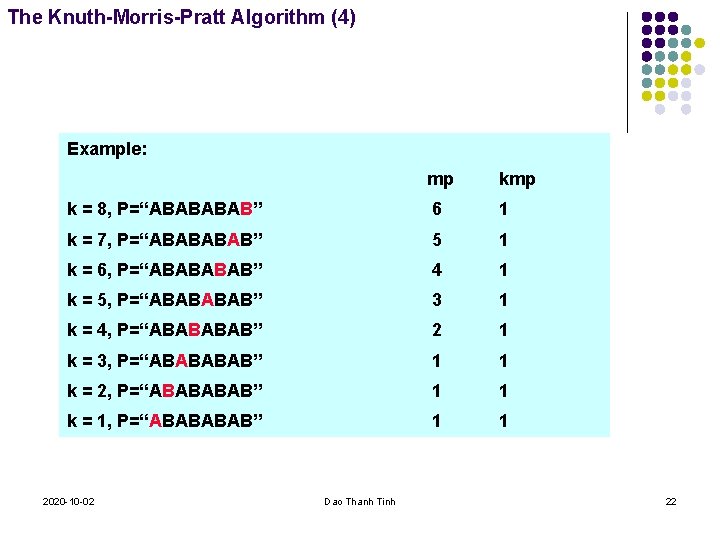
The Knuth-Morris-Pratt Algorithm (4) Example: mp k = 8, P=“ABAB” 6 1 k = 7, P=“ABAB” 5 1 k = 6, P=“ABAB” 4 1 k = 5, P=“ABAB” 3 1 k = 4, P=“ABAB” 2 1 k = 3, P=“ABAB” 1 1 k = 2, P=“ABAB” 1 1 k = 1, P=“ABAB” 1 1 2020 -10 -02 Dao Thanh Tinh 22

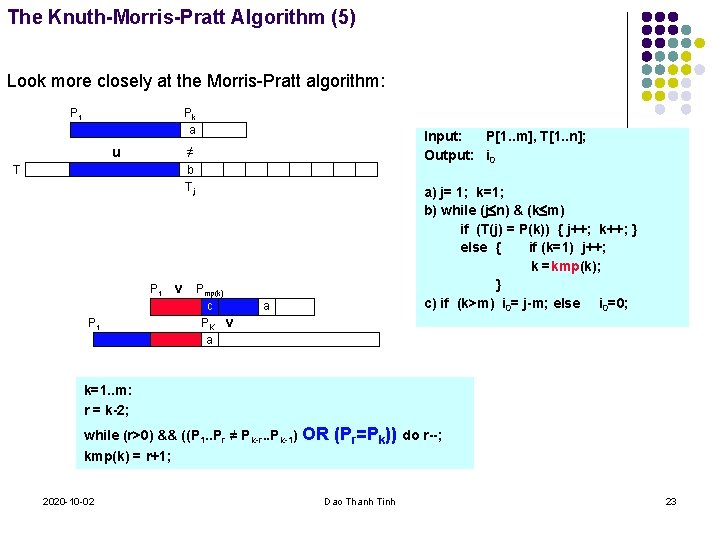
The Knuth-Morris-Pratt Algorithm (5) Look more closely at the Morris-Pratt algorithm: P 1 Pk a u Input: P[1. . m], T[1. . n]; Output: i 0 ≠ T b Tj P 1 v P 1 Pmp(k) c PK v a a) j= 1; k=1; b) while (j n) & (k m) if (T(j) = P(k)) { j++; k++; } else { if (k=1) j++; k =kmp(k); } c) if (k>m) i 0= j-m; else i 0=0; a k=1. . m: r = k-2; while (r>0) && ((P 1. . Pr ≠ Pk-r. . Pk-1) OR (Pr=Pk)) do r--; kmp(k) = r+1; 2020 -10 -02 Dao Thanh Tinh 23

The Brute Force Algorithm 2 Input: Output: P[1. . m], T[1. . n]; i 0 (if P T[i 0. . i 0+m-1], i 0 1, otherwise i 0=0) a) i=m; j= i; k=m; b) while (j n) & (k>0) if (T(j) = P(k)) { else { j--; k--; } i++; j=i+m; k=m; } c) if (k=0) i 0 : = i else i 0 : =0; Complexity: 2020 -10 -02 Example: P = DEABAB ║║ T = ABDEABABAA P = DEABAB ║║║║║║ T = ABDEABABAA, O(mn). successful match, i 0=3 Dao Thanh Tinh 24

The Brute Force Algorithm 2* Input: Output: P[1. . m], T[1. . n]; i 0 (if P T[i 0. . i 0+m-1], i 0 1, otherwise i 0=0) a) j= m; k=m; b) while (j n) & (k>0) if (T(j) = P(k)) { else j--; k--; P = DEABAB ║║ T = ABDEABABAA } { j = j+m-k+1; k=m; } c) if (k=0) i 0 : = j-m else i 0 : =0 Complexity: 2020 -10 -02 Example: P = DEABAB T = ABDEABABAA P = DEABAB ║║║║║║ T = ABDEABABAA, successful match, i 0=3 O(mn). Dao Thanh Tinh 25

The Boyer-Moore Algorithm (1) m-k-1 Pk Pk+1 Pm u Tj+m-k Tj Tj+1 T[j] P[k], 2020 -10 -02 T[j+1. . j+m-k] = P[k+1. . m] = u Dao Thanh Tinh 26

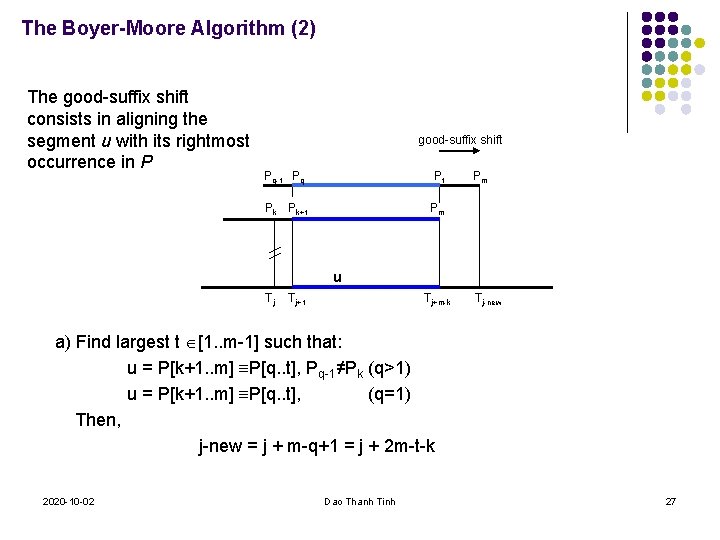
The Boyer-Moore Algorithm (2) The good-suffix shift consists in aligning the segment u with its rightmost occurrence in P good-suffix shift Pq-1 Pq Pt Pk Pk+1 Pm Pm u Tj Tj+1 Tj+m-k Tj-new a) Find largest t [1. . m-1] such that: u = P[k+1. . m] P[q. . t], Pq-1≠Pk (q>1) u = P[k+1. . m] P[q. . t], (q=1) Then, j-new = j + m-q+1 = j + 2 m-t-k 2020 -10 -02 Dao Thanh Tinh 27

The Boyer-Moore Algorithm (3) b) If not exists t [1. . m-1] such that: u = P[k+1. . m] P[q. . t] the shift consists in aligning the longest suffix v of P with a matching prefix of P Find largest t [1. . m-1] such that: Then, j-new = j + 2 m-t-k u = P[m-t+1. . m] P[1. . t], good-suffix shift P 1 Pk Pk+1 Pm-t+1 Tj 2020 -10 -02 Pt v Tj+1 Pm Tj+m-k Dao Thanh Tinh Pm Tj-new 28

The Boyer-Moore Algorithm (4) c) If not exists t [1. . m-1] such that: u = P[m-t+1. . m] P[1. . t] Then, or j-new = j + 2 m-k-t, where t=0 good-suffix shift P 1 Pk Pk+1 Tj 2020 -10 -02 Tj+1 Pm Pm Tj+m-k Dao Thanh Tinh Tj-new 29

The Boyer-Moore Algorithm (5) d) If Tj [P 1. . . Pm] : then, j-new = j + m good-suffix shift P 1 Pk Pk+1 Tj 2020 -10 -02 Tj+1 Pm Pm Tj+m-k Tj-new Dao Thanh Tinh 30

The Boyer-Moore Algorithm (6) a) j=m; k=m; b) while (j n) & (k>0) if T(j) = P(k) { j--; k--; } else { k = m; j = jnew; } c) if (k=0) i 0= j+1; else Complexity: i 0= 0; O(nm) remark: Jnew and j+1 are the new components on comparison with Brute Force Algorithm. 2020 -10 -02 Dao Thanh Tinh 31

The Boyer-Moore Algorithm (7) Computing Jnew ? 2020 -10 -02 Dao Thanh Tinh 32

The Boyer-Moore Algorithm (8) a) Find largest t [1. . m-1] such that: u = P[k+1. . m] P[q. . t], Pq-1≠Pk (q>1) u = P[k+1. . m] P[q. . t], (q=1) Then, j-new = j + m-q+1 = j + 2 m-t-k good-suffix shift Pq-1 Pq Pt Pk Pk+1 Pm Pm u Tj Tj+1 Tj+m-k Tj-new a) bmg(k) = 2 m-k-t t = m-1; while (t>m-k) & (P[k+1. . m] ≠P[t-m+k+1. . t]) OR (Pt-m+k=Pk) if (t=m-k) & P[k+1. . m] ≠ P[1. . t]) t=0; t=t-1; remark: when t=0, bmg(k) = 2 m-k; 2020 -10 -02 Dao Thanh Tinh 33

The Boyer-Moore Algorithm (9) b) If not exists t [1. . m-1] such that: u = P[k+1. . m] P[q. . t] the shift consists in aligning the longest suffix v of P with a matching prefix of P Find largest t [1. . m-1] such that: Then, j-new = j + 2 m-k-t u = P[m-t+1. . m] P[1. . t], b) bmg(k) = 2 m-k-t t = m - k-1; while (t>0) & (P[m-t+1. . m] ≠P[1. . t]) t = t-1; if (t=m-k+2) & P[k+1. . m] ≠ P[1. . t]) t=0; good-suffix shift remark: when t=0, bmg(k) = 2 m-k; P 1 Pt Pk Pk+1 Pm-t+1 Pm Pm v Tj 2020 -10 -02 Tj+1 Dao Thanh Tinh Tj+m-k Tj-new 34

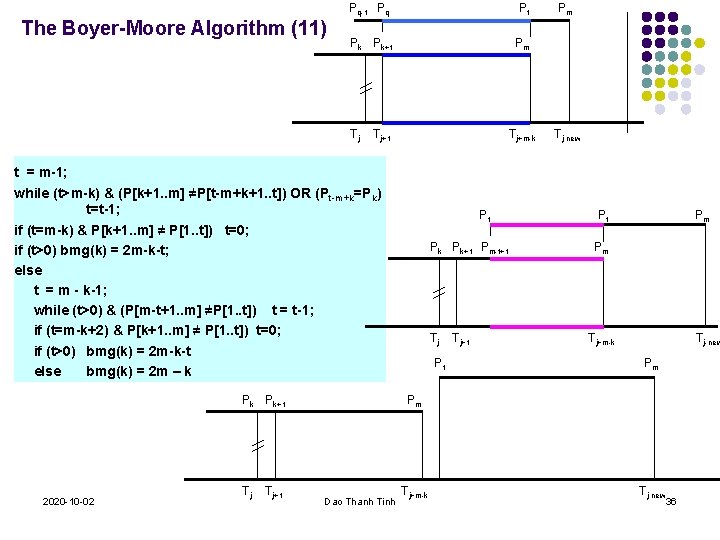
The Boyer-Moore Algorithm (10) c) If not exists t [1. . m-1] such that: Then, or u = P[m-t+1. . m] P[1. . t] j-new = j + 2 m-k-t, where t=0 c) bmg(k) = 2 m – k - t where t = 0 good-suffix shift P 1 Pk Pk+1 Tj 2020 -10 -02 Tj+1 Pm Pm Tj+m-k Dao Thanh Tinh Tj-new 35

The Boyer-Moore Algorithm (11) Pq-1 Pq Pt Pk Pk+1 Pm Tj Tj+1 Tj+m-k t = m-1; while (t>m-k) & (P[k+1. . m] ≠P[t-m+k+1. . t]) OR (Pt-m+k=Pk) t=t-1; if (t=m-k) & P[k+1. . m] ≠ P[1. . t]) t=0; if (t>0) bmg(k) = 2 m-k-t; else t = m - k-1; while (t>0) & (P[m-t+1. . m] ≠P[1. . t]) t = t-1; if (t=m-k+2) & P[k+1. . m] ≠ P[1. . t]) t=0; if (t>0) bmg(k) = 2 m-k-t else bmg(k) = 2 m – k Pk Pk+1 2020 -10 -02 Tj Tj+1 P 1 Pk Pk+1 Pm-t+1 Tj P 1 Tj+1 Pm Tj-new Pt Pm Pm Tj+m-k Tj-new Pm Pm Dao Thanh Tinh Tj+m-k Tj-new 36

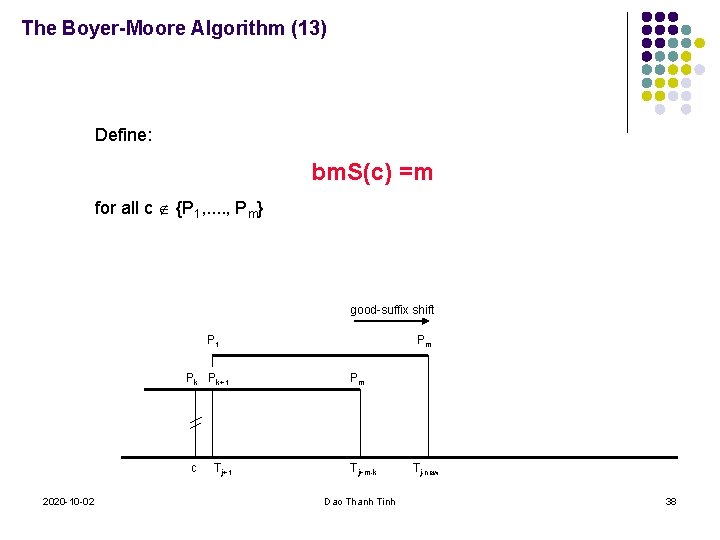
The Boyer-Moore Algorithm (12) d) If Tj [P 1. . . Pm] : then, the left end of the window is aligned with the character immediately after Tj, namely Tj+1. j-new = j + m d) bm. S(Tj) = m but Tj {P 1, . . . , Pm} ? good-suffix shift P 1 Pk Pk+1 Pm Pm Tj-new Tj 2020 -10 -02 Tj+1 Tj+m-k Dao Thanh Tinh 37

The Boyer-Moore Algorithm (13) Define: bm. S(c) =m for all c {P 1, . . , Pm} good-suffix shift P 1 Pk Pk+1 c 2020 -10 -02 Tj+1 Pm Pm Tj+m-k Dao Thanh Tinh Tj-new 38

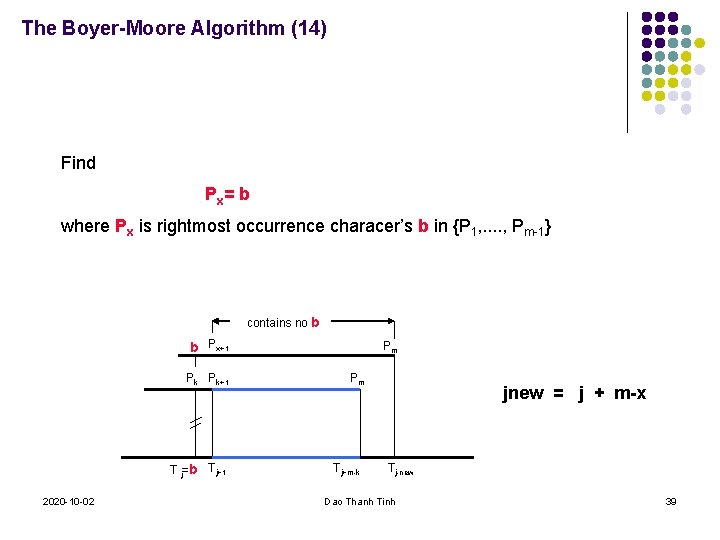
The Boyer-Moore Algorithm (14) Find Px= b where Px is rightmost occurrence characer’s b in {P 1, . . , Pm-1} contains no b b Px+1 Pk Pk+1 T j=b Tj+1 2020 -10 -02 Pm Pm Tj+m-k jnew = j + m-x Tj-new Dao Thanh Tinh 39

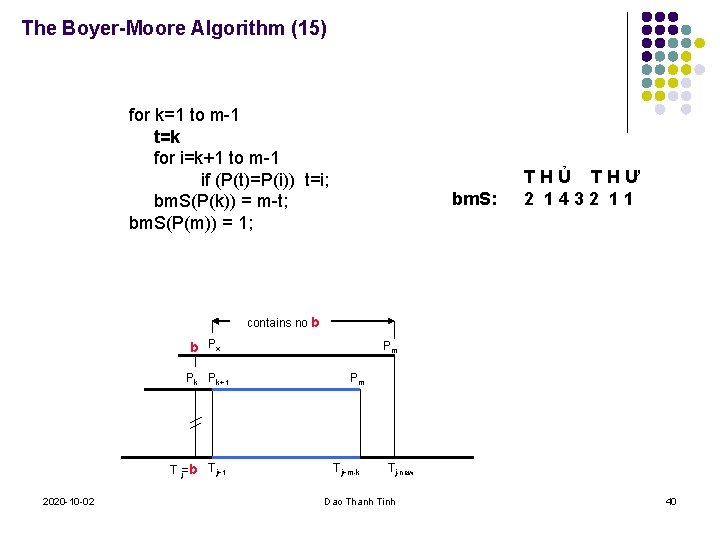
The Boyer-Moore Algorithm (15) for k=1 to m-1 t=k for i=k+1 to m-1 if (P(t)=P(i)) t=i; bm. S(P(k)) = m-t; bm. S(P(m)) = 1; bm. S: THỦ THƯ 2 1432 11 contains no b b Px Pk Pk+1 T j=b Tj+1 2020 -10 -02 Pm Pm Tj+m-k Tj-new Dao Thanh Tinh 40

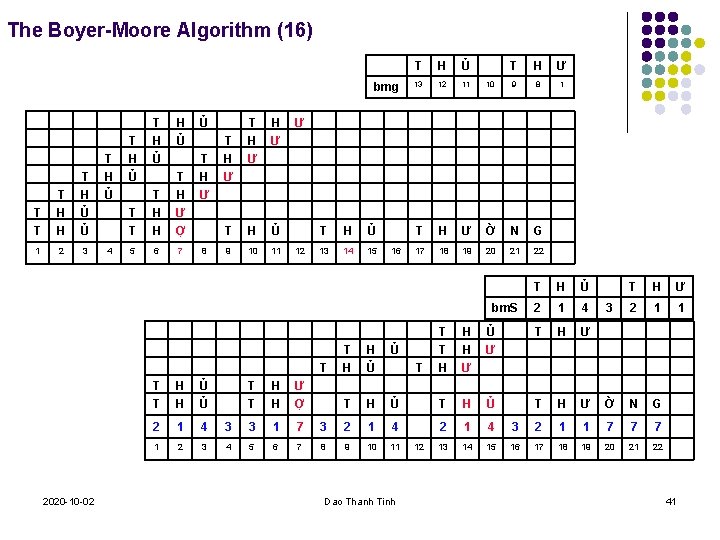
The Boyer-Moore Algorithm (16) bmg T T T H H T H Ủ Ủ 1 2 3 T H Ủ 4 T H Ủ H Ủ T T T H H T H Ư Ợ 5 6 7 Ủ T H Ư 8 T H Ư T H Ủ 9 10 11 T H Ư T H Ủ T H Ư 13 12 11 10 9 8 1 T H Ư Ờ N G 17 18 19 20 21 22 Ư 12 T H Ủ 13 14 15 16 bm. S T 2020 -10 -02 T T H H Ủ Ủ 2 1 4 1 2 3 T H Ủ 2 1 4 T H Ư 3 2 1 1 T T H H H Ư Ủ Ư T H Ư Ờ N G T H H Ủ Ủ T H Ủ 2 1 4 3 2 1 1 7 7 7 13 14 15 16 17 18 19 20 21 22 T T T H H Ư Ợ 3 3 1 7 3 2 1 4 4 5 6 7 8 9 10 11 Dao Thanh Tinh 12 41

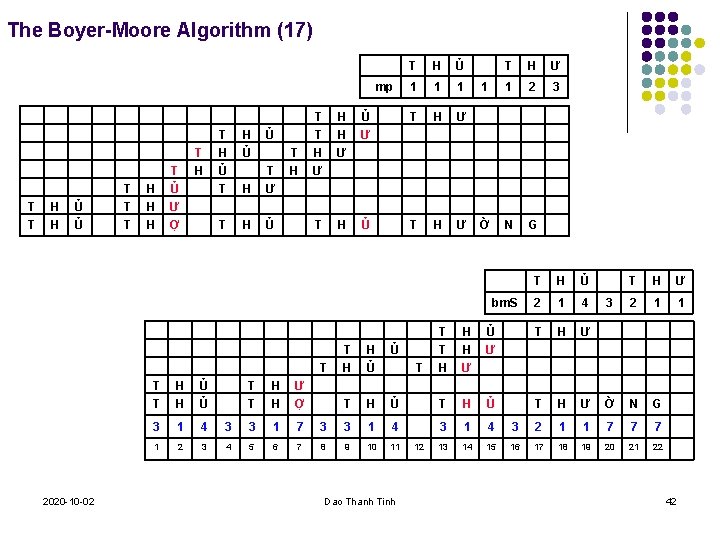
The Boyer-Moore Algorithm (17) mp T T H H Ủ Ủ T T T H H H T Ủ Ư Ợ T H Ủ Ủ H T Ư T H Ủ 1 1 1 T T H Ư H H Ư Ủ Ư T H Ủ T H Ư 1 1 2 3 Ờ N G bm. S T 2020 -10 -02 T T H H Ủ Ủ 3 1 4 1 2 3 T H Ủ 2 1 4 T H Ư 3 2 1 1 T T H H H Ư Ủ Ư T H Ư Ờ N G T H H Ủ Ủ T H Ủ 3 1 4 3 2 1 1 7 7 7 13 14 15 16 17 18 19 20 21 22 T T T H H Ư Ợ 3 3 1 7 3 3 1 4 4 5 6 7 8 9 10 11 Dao Thanh Tinh 12 42

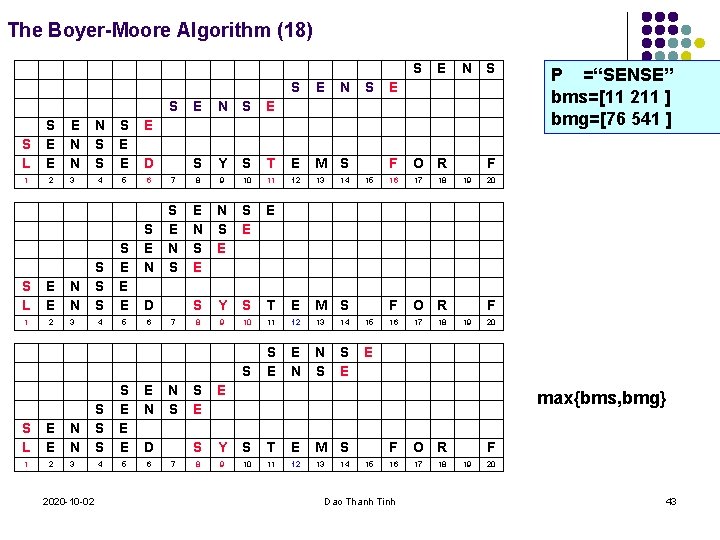
The Boyer-Moore Algorithm (18) S S L S E E 1 2 S L E E 1 2 E N N 3 2020 -10 -02 E N S S E N E F O R 15 16 17 18 F O R 16 17 18 E S Y S T E M S 4 5 6 7 8 9 10 11 12 13 E N S E S E N S S Y S T E M S 8 9 10 11 12 13 14 15 E N N S S E E S S S 4 5 D 6 S S E E N 4 5 6 7 N S D 7 N S 19 20 E S E E E E S N S S D S 14 S E E S Y S T E M S 8 9 10 11 12 13 P =“SENSE” bms=[11 211 ] bmg=[76 541 ] F F 19 20 max{bms, bmg} 14 15 F O R 16 17 18 Dao Thanh Tinh F 19 20 43

The Karp-Rabin Algorithm Giả thiết = {1, 2, . . . , 9} p = ts ? s {1, . . . , n-m+1}: ts = p ? 2020 -10 -02 Dao Thanh Tinh 44

The Karp-Rabin Algorithm (2) Tính p theo sơ đồ Horner’s : { { p= P(m) + 10* P(m-1)+ 10* P(m-2)+. . +10*{P(2)+10*P(1)}. . }} p=P(1) for i=2 to m do p = P(i) + 10*p; Thời gian tính: O(m) 2020 -10 -02 Dao Thanh Tinh 45

The Karp-Rabin Algorithm (3) Tính ts: ts = 10 m-1 T(s) + 10 m-2 T(s+1)+10 m-3 T(s+2). . . +10 T(s+m-2)+T(s+m-1) ts+1 = 10 m-1 T(s+1) + 10 m-2 T(s+2)+. . . +102 T(s+m-2)+10 T(s+m-1)+T(s+m) { } = 10 10 m-2 T(s+1) + 10 m-3 T(s+2)+. . . +10 T(s+m-2)+T(s+m-1) +T(s+m) { } = 10 ts – 10 m-1 T(s) + T(s+m) 2020 -10 -02 Dao Thanh Tinh 46

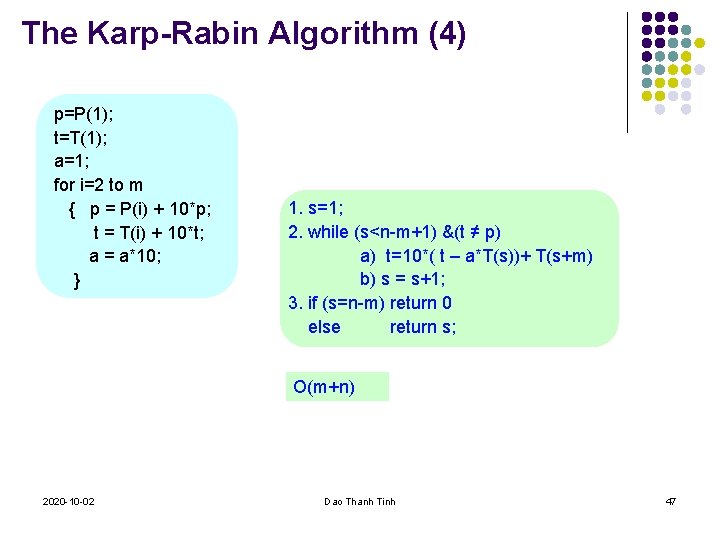
The Karp-Rabin Algorithm (4) p=P(1); t=T(1); a=1; for i=2 to m { p = P(i) + 10*p; t = T(i) + 10*t; a = a*10; } 1. s=1; 2. while (s<n-m+1) &(t ≠ p) a) t=10*( t – a*T(s))+ T(s+m) b) s = s+1; 3. if (s=n-m) return 0 else return s; O(m+n) 2020 -10 -02 Dao Thanh Tinh 47

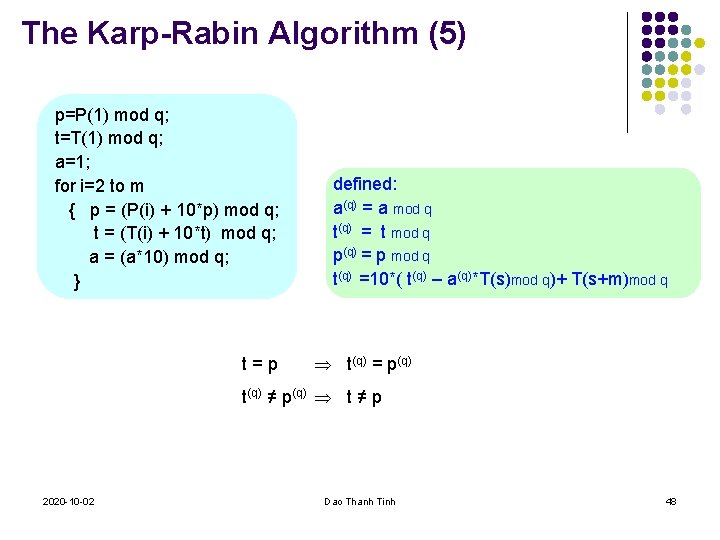
The Karp-Rabin Algorithm (5) p=P(1) mod q; t=T(1) mod q; a=1; for i=2 to m { p = (P(i) + 10*p) mod q; t = (T(i) + 10*t) mod q; a = (a*10) mod q; } t=p defined: a(q) = a mod q t(q) = t mod q p(q) = p mod q t(q) =10*( t(q) – a(q)*T(s)mod q)+ T(s+m)mod q t(q) = p(q) t(q) ≠ p(q) t ≠ p 2020 -10 -02 Dao Thanh Tinh 48

The Karp-Rabin Algorithm (6) p=P(1) mod q; t=T(1) mod q; a=1; for i=2 to m { p = (P(i) + 10*p) mod q; t = (T(i) + 10*t) mod q; a = (a*10) mod q; } 2020 -10 -02 s=1; while(s<m-n+1) if (t(q)=p(q)) if (P=Ts) return s; else t(q) =10*( t(q) – a(q)*T(s)mod q)+ T(s+m)mod q s = s+1; Dao Thanh Tinh 49

Conclusion Brute Force Algorithm 1: Straightforward Matching The Morris-Pratt Algorithm Knuth-Morris-Pratt Algorithm Brute Force Algorithm 2: Backing The Boyer-Moore Algorithm The Karp-Rabin Algorithm 2020 -10 -02 Dao Thanh Tinh 50