Relaes tenso deformao Resistncia ao Corte Relaes TensoDeformao
























- Slides: 59

Relações tensão deformação Resistência ao Corte

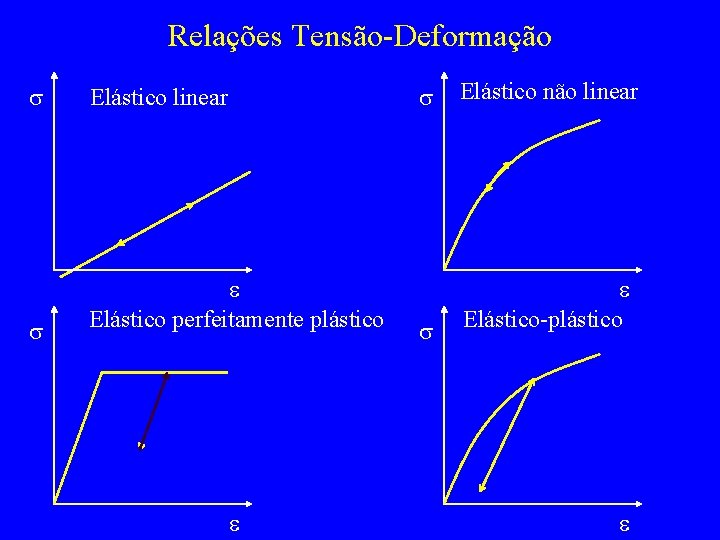
Relações Tensão-Deformação s s s Elástico linear e Elástico perfeitamente plástico e s Elástico não linear e Elástico-plástico e

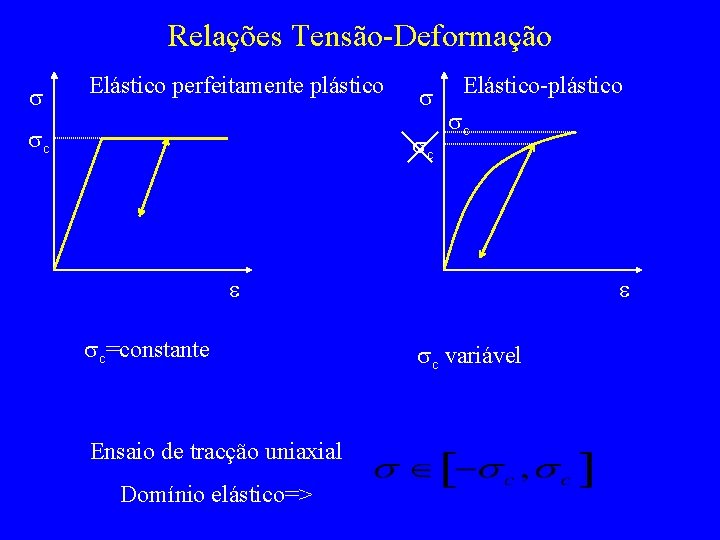
Relações Tensão-Deformação s Elástico perfeitamente plástico sc s sc Elástico-plástico sc e sc=constante Ensaio de tracção uniaxial Domínio elástico=> e sc variável

Solos? è Critério de rotura não pode ser definido unidimensionalmente è Definição de critério de ruptura no espaço das tensões

Solos - resistência è Solos: materiais friccionais – resistência depende da tensão aplicada è A resistência ao corte é controlada pelas tensões efectivas è A resistência ao corte depende do tipo de carregamento – A resistência medida será diferente conforme » Há deformação a volume constante (carregamento não drenado) » Não há desenvolvimento de pressões intersticiais (carregamento drenado)

Ensaio de corte directo N T SOLO Pedra Porosa

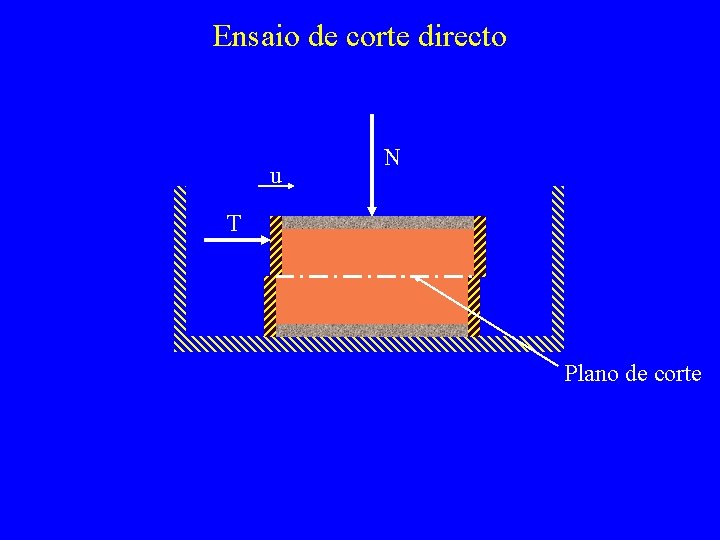
Ensaio de corte directo u N T Plano de corte


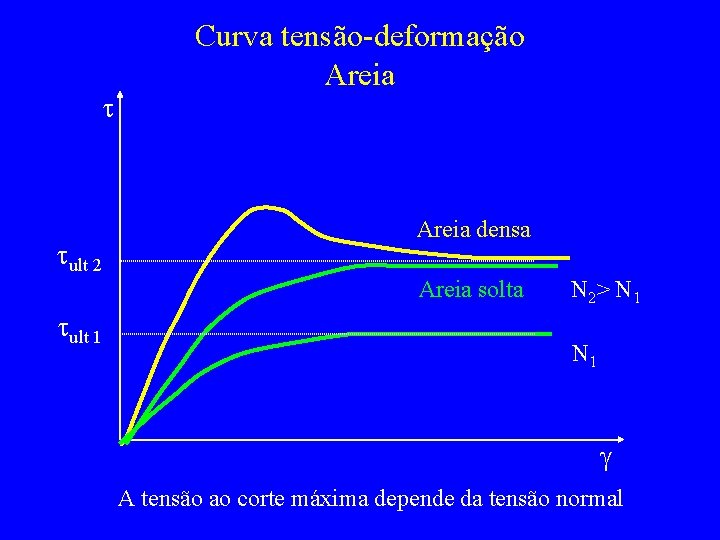
t tult 2 Curva tensão-deformação Areia densa Areia solta tult 1 N 2> N 1 g A tensão ao corte máxima depende da tensão normal

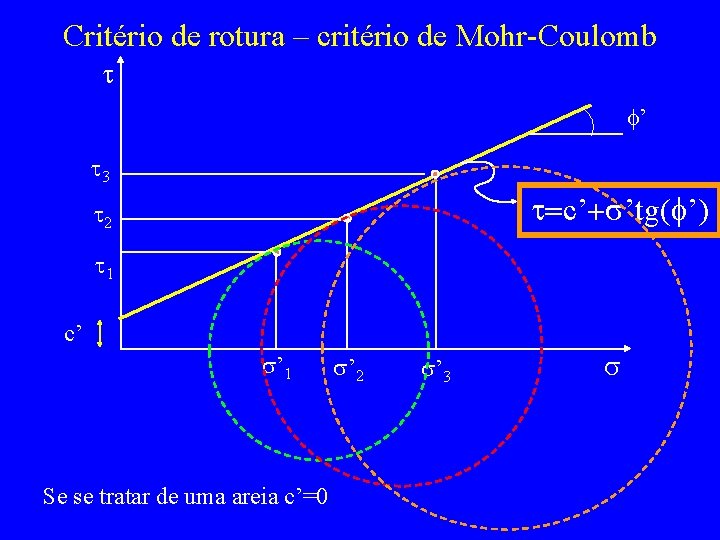
Critério de rotura – critério de Mohr-Coulomb t f’ t 3 t=c’+s’tg(f’) t 2 t 1 c’ s’ 1 Se se tratar de uma areia c’=0 s’ 2 s’ 3 s

Problemas è Num ensaio de corte directo de uma areia a rotura é alcançada com s=100 k. Pa e t=65 k. Pa. – Determine o ângulo de atrito dessa areia. – Qual o ângulo que faz com a horizontal o plano onde a tensão normal é máxima?

Problemas è Campos de tensão não uniformes – Tensões macroscópicas podem ser diferentes das microscópicas que levam à ruptura è Redução è Não da secção transversal existe controlo sobre a drenagem

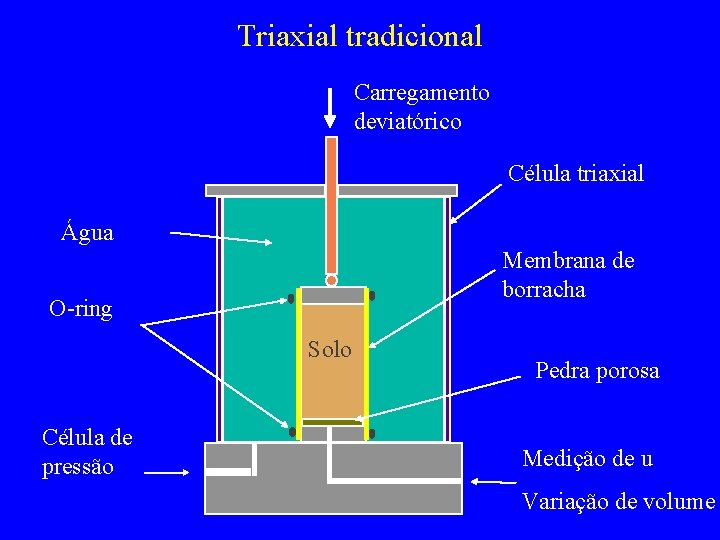
Triaxial tradicional Carregamento deviatórico Célula triaxial Água Membrana de borracha O-ring Solo Célula de pressão Pedra porosa Medição de u Variação de volume


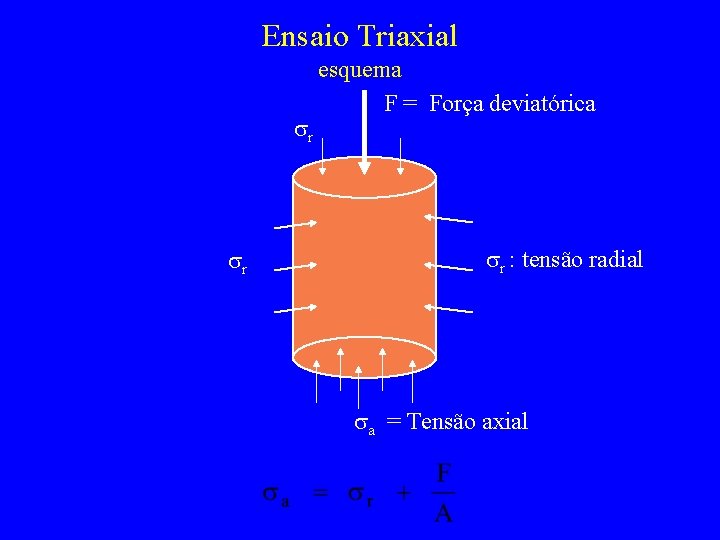
Ensaio Triaxial sr sr esquema F = Força deviatórica sr : tensão radial sa = Tensão axial

Tensões no ensaio triaxial è q=sa-sr: tensão deviatórica è p= (sa+2 sr )/3: tensão média (isotrópica) è t=(sa-sr)/2 : raio do círculo de Mohr è s=(sa+sr )/2 : centro do círculo de Mohr

Deformações no ensaio triaxial è Deformação axial ea è Deformação volumétrica ev = ea+2 er=DV/V 0 è Deformação deviatórica es =2/3(ea - er)

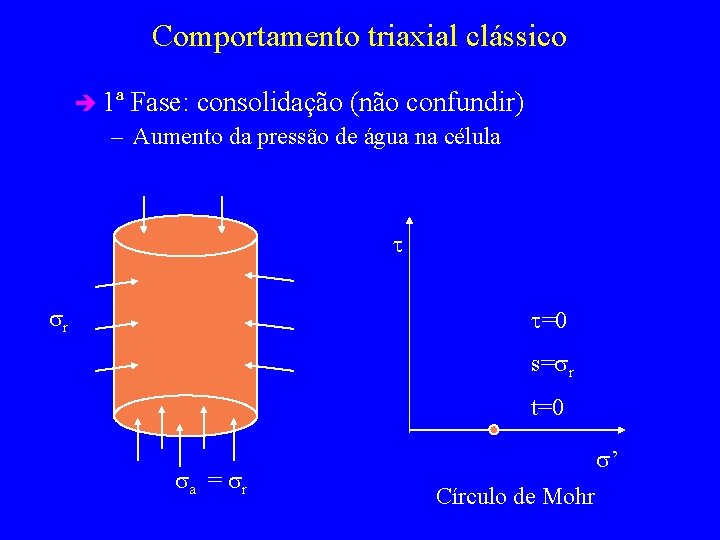
Comportamento triaxial clássico è 1ª Fase: consolidação (não confundir) – Aumento da pressão de água na célula t sr t=0 s=sr t=0 sa = sr s’ Círculo de Mohr

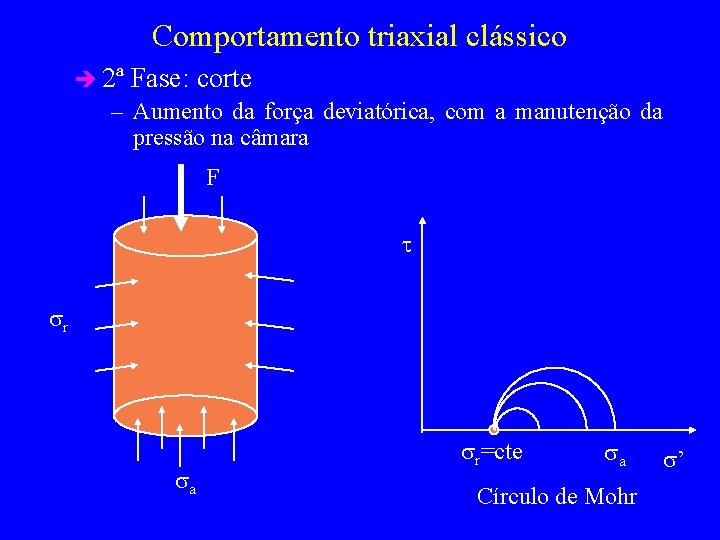
Comportamento triaxial clássico è 2ª Fase: corte – Aumento da força deviatórica, com a manutenção da pressão na câmara F t sr sa sr=cte sa Círculo de Mohr s’

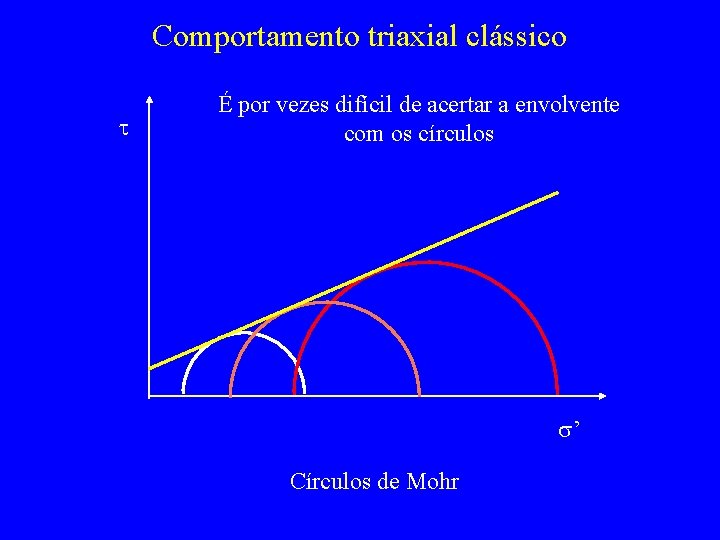
Comportamento triaxial clássico t É por vezes difícil de acertar a envolvente com os círculos s’ Círculos de Mohr

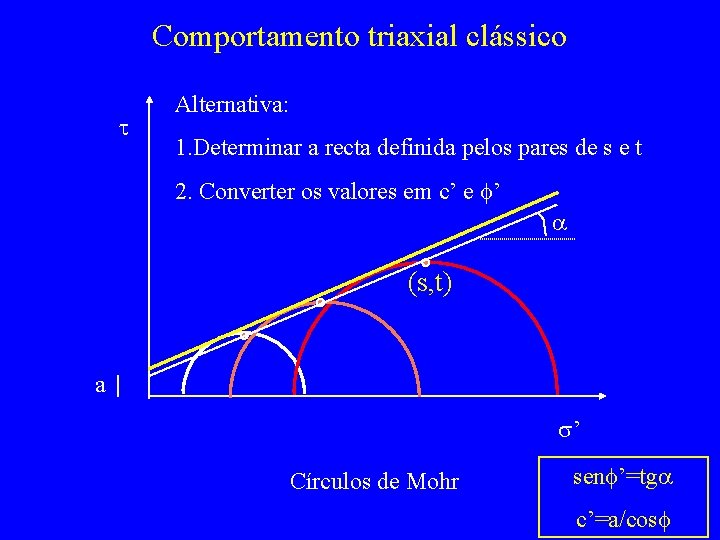
Comportamento triaxial clássico t Alternativa: 1. Determinar a recta definida pelos pares de s e t 2. Converter os valores em c’ e f’ a (s, t) a s’ Círculos de Mohr senf’=tga c’=a/cosf

Problemas è Um ensaio triaxial conduzido sobre três provetes de areia conduziu aos seguintes resultados na rotura è Determine Teste nº s’ 3 s’ 1 k. Pa 1 100 350 2 180 542 3 300 864 o ângulo de atrito de cada amostra è Determine um ângulo de atrito para o material


Ensaio Triaxial è Ensaios Consolidados Drenados – CD è Ensaios Consolidados não Drenados – CU è Ensaios não Consolidados não Drenados – UU

Ensaios Consolidados Drenados – CD 1ª fase : consolidação (Du=0 ) Ds 1 Du=0 => Ds’=Ds Ds 1=Ds 3

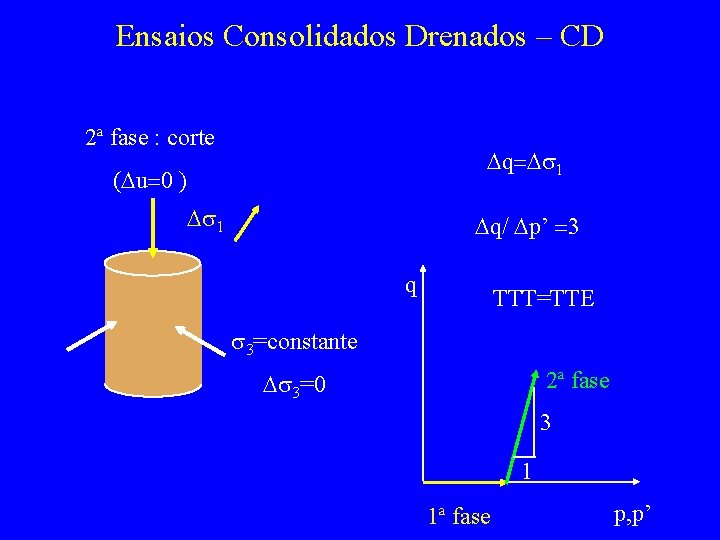
Ensaios Consolidados Drenados – CD 2ª fase : corte Dq=Ds 1 (Du=0 ) Ds 1 Dq/ Dp’ =3 q TTT=TTE s 3=constante 2ª fase Ds 3=0 3 1 1ª fase p, p’

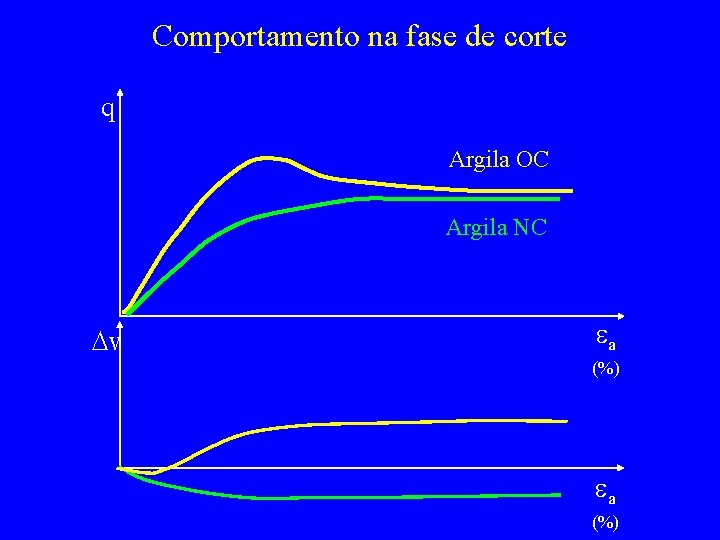
Comportamento na fase de corte q Argila OC Argila NC Dv ea (%)

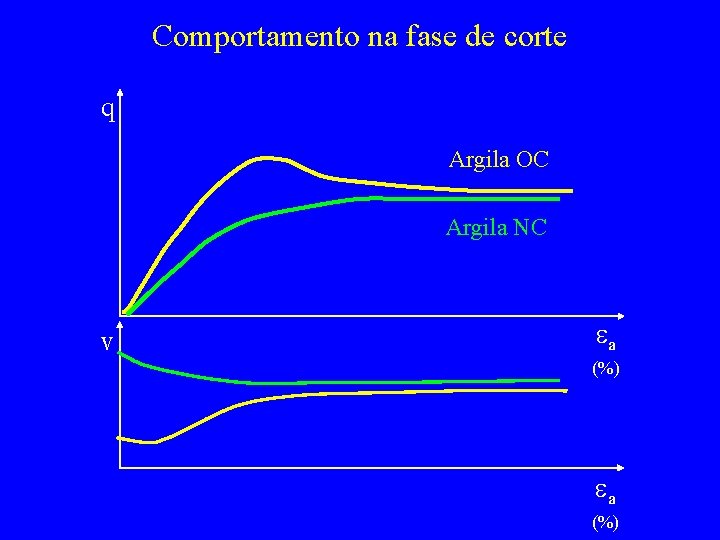
Comportamento na fase de corte q Argila OC Argila NC v ea (%)

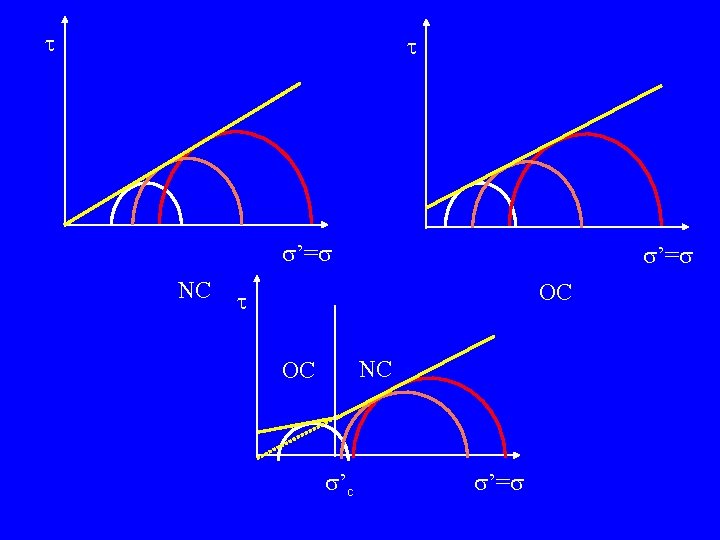
t t s’=s NC s’=s OC t NC OC s’c s’=s

Ensaios Consolidados não Drenados – CU 1ª fase : consolidação (Du=0 ) Ds 1 Du=0 => Ds’=Ds Ds 1=Ds 3

Ensaios Consolidados não Drenados – CU 2ª fase : corte Dq=Ds 1 (Du 0 , V=cte) Ds 1 q s 3=constante Ds 3=0 Du TTT TTE 3 1 1ª fase TTE=TTT p, p’

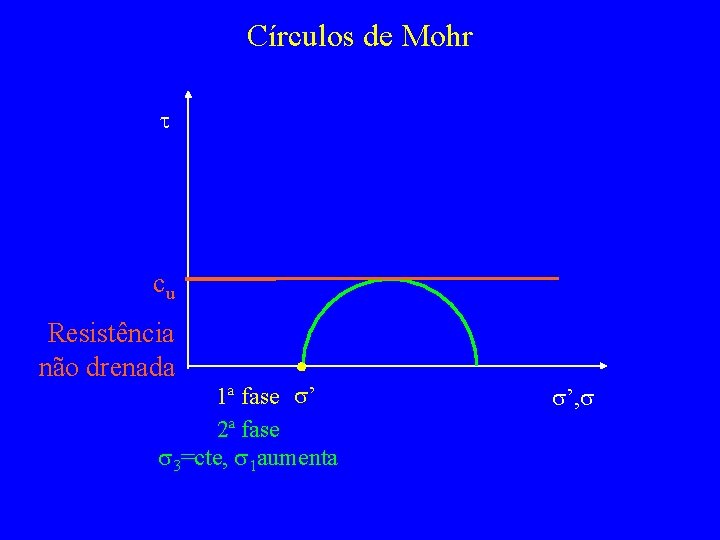
Círculos de Mohr t cu Resistência não drenada 1ª fase s’ 2ª fase s 3=cte, s 1 aumenta s’, s

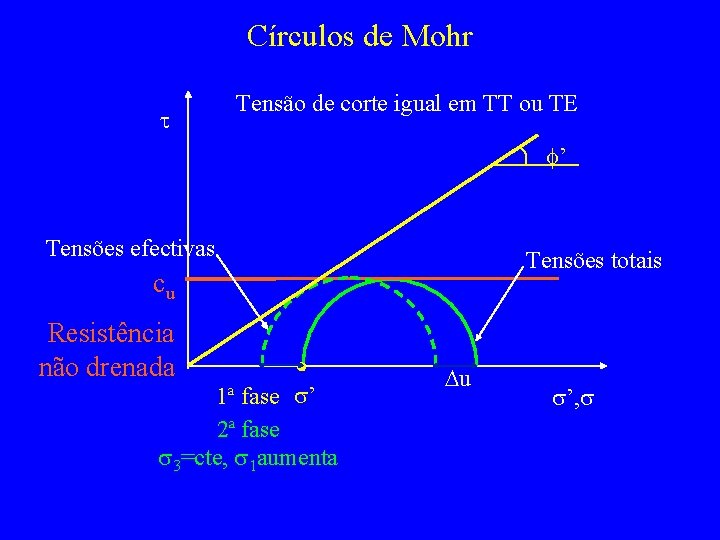
Círculos de Mohr t Tensão de corte igual em TT ou TE f’ Tensões efectivas Tensões totais cu Resistência não drenada 1ª fase s’ 2ª fase s 3=cte, s 1 aumenta Du s’, s

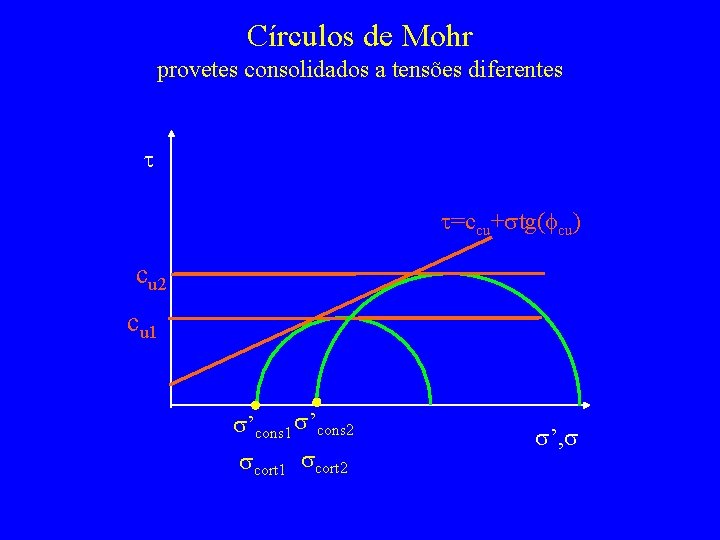
Círculos de Mohr provetes consolidados a tensões diferentes t t=ccu+stg(fcu) cu 2 cu 1 s’cons 2 scort 1 scort 2 s’, s

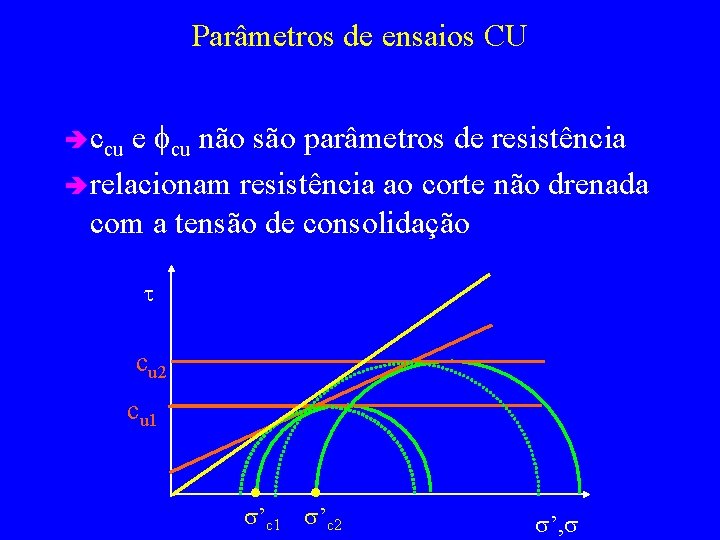
Parâmetros de ensaios CU e fcu não são parâmetros de resistência è relacionam resistência ao corte não drenada com a tensão de consolidação è ccu t cu 2 cu 1 s’c 2 s’, s

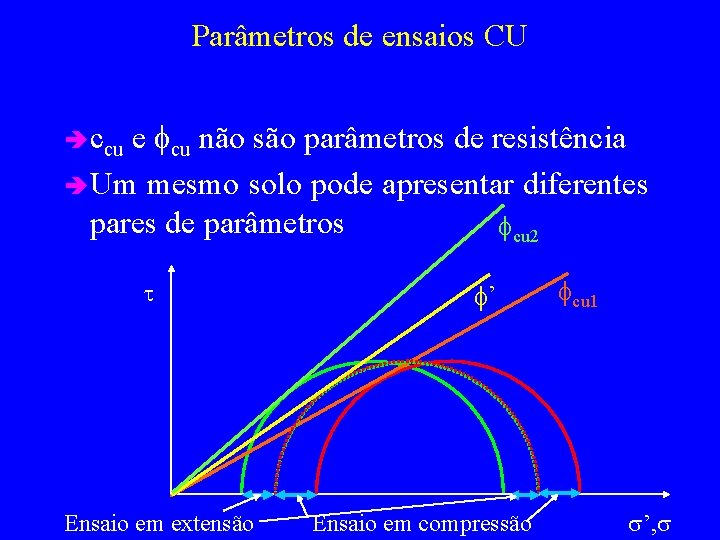
Parâmetros de ensaios CU e fcu não são parâmetros de resistência è Um mesmo solo pode apresentar diferentes pares de parâmetros fcu 2 è ccu t Ensaio em extensão f’ Ensaio em compressão fcu 1 s’, s

Ensaios não Consolidados não Drenados – UU 1ª fase : consolidação (cuidado!) 2ª fase : corte (DV=0 => Du 0 ) Ds 1=Ds 3 s 3=constante Ds 3=0

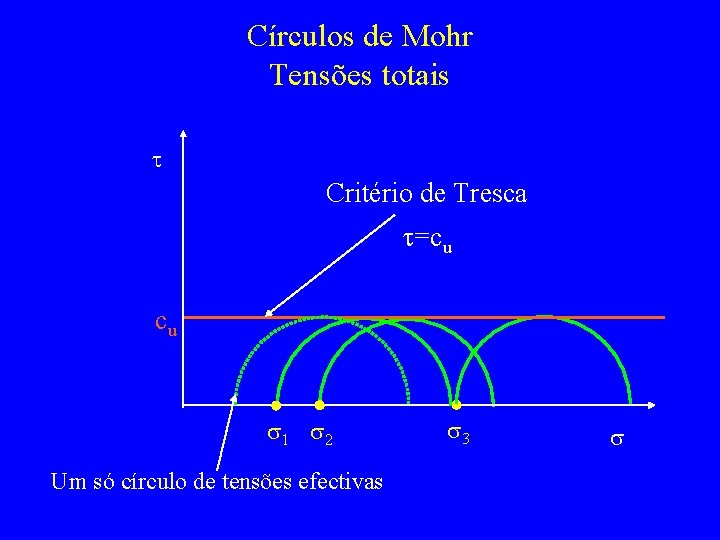
Círculos de Mohr Tensões totais t Critério de Tresca t=cu cu s 1 s 2 Um só círculo de tensões efectivas s 3 s

Evolução da pressão intersticial Expressão de Skempton è Se solo saturado B=1 Tipo de solo Parâmetro A Argilas NC 0, 7 a 1, 3 Argilas ligeiramente OC 0, 3 a 0, 7 Argilas medianamente OC 0, 0 a 0, 3 Argilas fortemente OC <0, 0

Problema è Executou-se um ensaio CU utilizando três provetes de uma argila saturada. A rotura ocorreu por aumento da tensão axial. Sabendo que na rotura os valores obtidos são os indicados na tabela calcule A; ccu e fcu; c’ e f’. Provete s 3 s 1 u A 1 150 310 70 0, 44 2 200 410 96 0, 46 3 300 620 141 0, 44

Problema è Executou-se um ensaio CU numa argila NC saturada. Na ruptura registaram-se os seguintes valores provete foi consolidado para uma tensão de 150 k. Pa, tensão que foi mantida na câmara durante a fase de corte. A rotura ocorreu por aumento da tensão axial, quando o pistão aplicava uma tensão de 160 k. Pa e a pressão u era de 54 k. Pa. Calcule A, cu e f’.

Ensaios com outras trajectórias de tensão 1ª fase : consolidação Ds 1= Dscâmara+ Dspistão Dp≠ 0 Ds 1= Dscâmara Dq≠ 0

Ensaios com outras trajectórias de tensão Dq/ Dp’ ≠ 3 2ª fase : corte Ds 1 q s 3 ≠ constante 2ª fase Ds 3≠ 0 1ª fase p

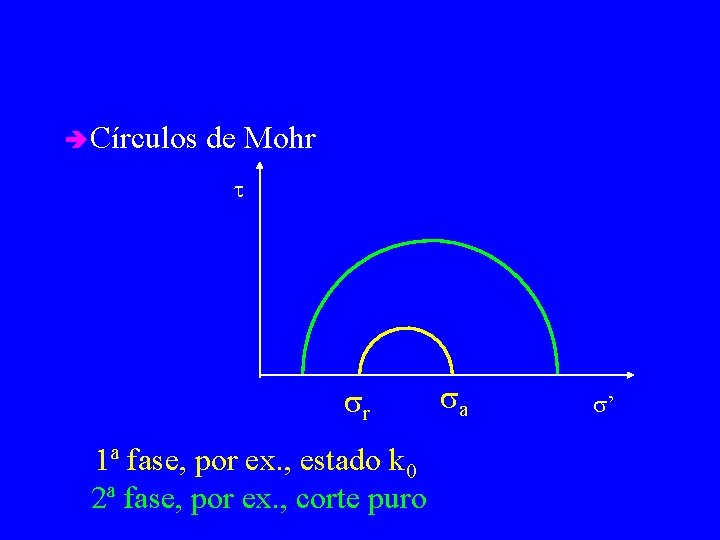
è Círculos de Mohr t sr 1ª fase, por ex. , estado k 0 2ª fase, por ex. , corte puro sa s’

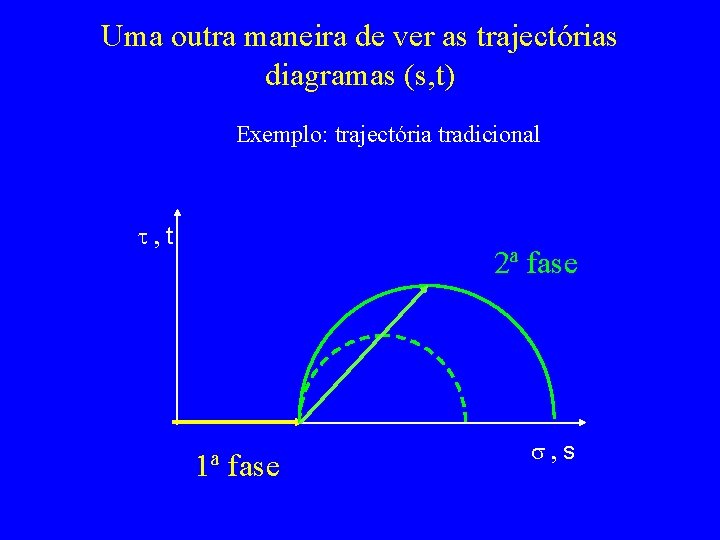
Uma outra maneira de ver as trajectórias diagramas (s, t) Exemplo: trajectória tradicional t, t 2ª fase 1ª fase s, s

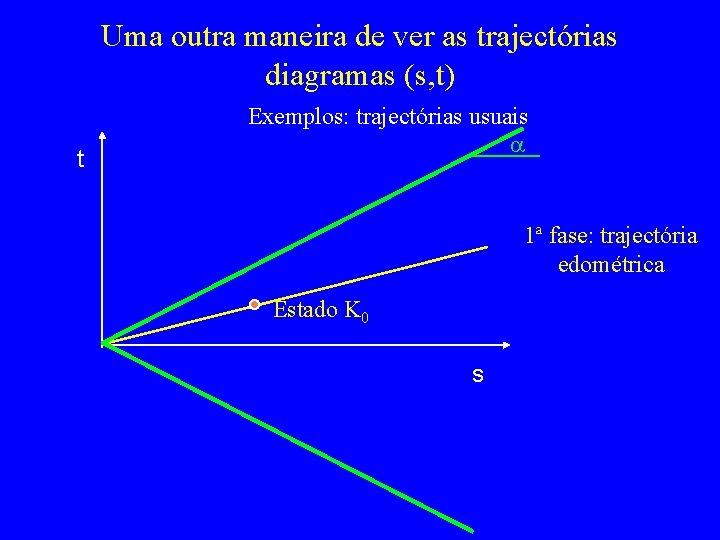
Uma outra maneira de ver as trajectórias diagramas (s, t) t Exemplos: trajectórias usuais a 1ª fase: trajectória edométrica Estado K 0 s

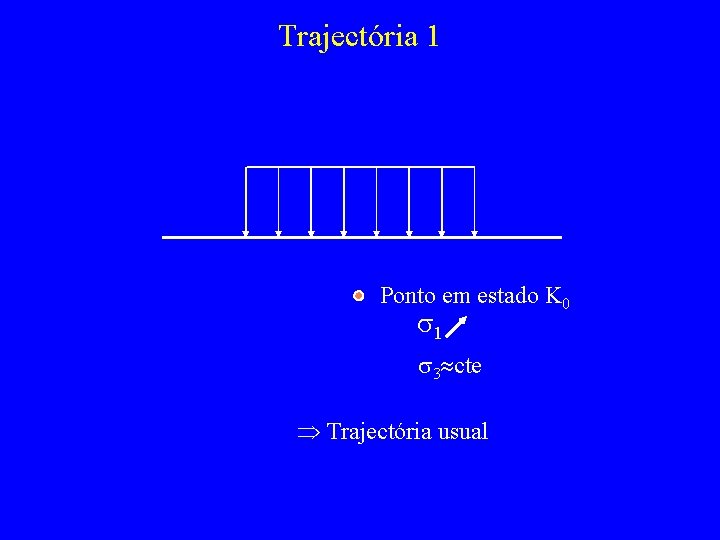
Trajectória 1 Ponto em estado K 0 s 1 s 3 cte Trajectória usual

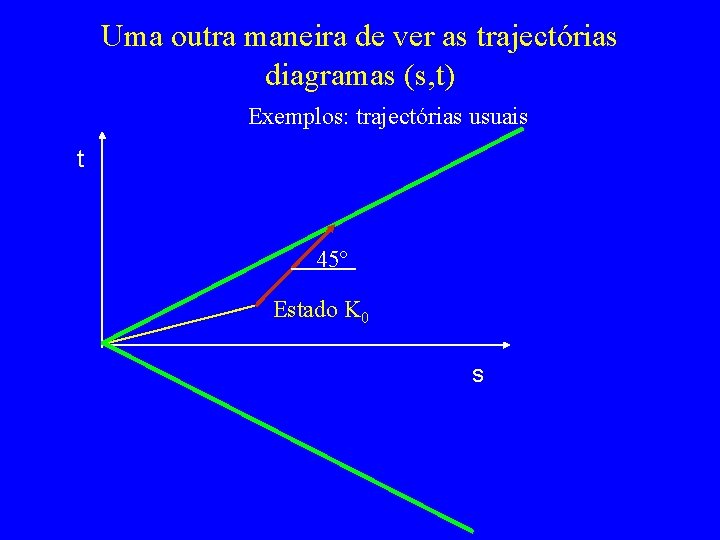
Uma outra maneira de ver as trajectórias diagramas (s, t) Exemplos: trajectórias usuais t 45º Estado K 0 s

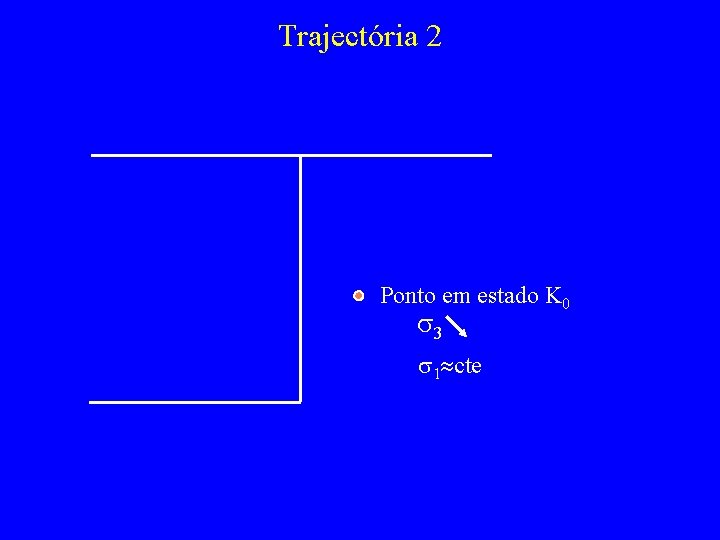
Trajectória 2 Ponto em estado K 0 s 3 s 1 cte

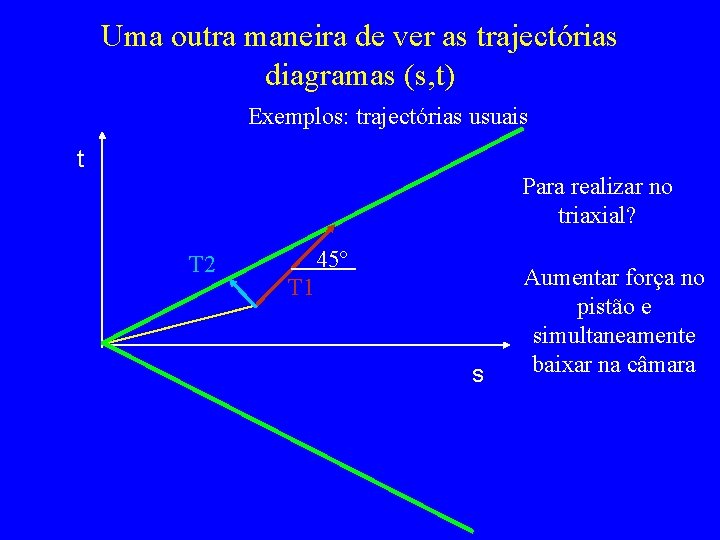
Uma outra maneira de ver as trajectórias diagramas (s, t) Exemplos: trajectórias usuais t Para realizar no triaxial? T 2 45º T 1 s Aumentar força no pistão e simultaneamente baixar na câmara

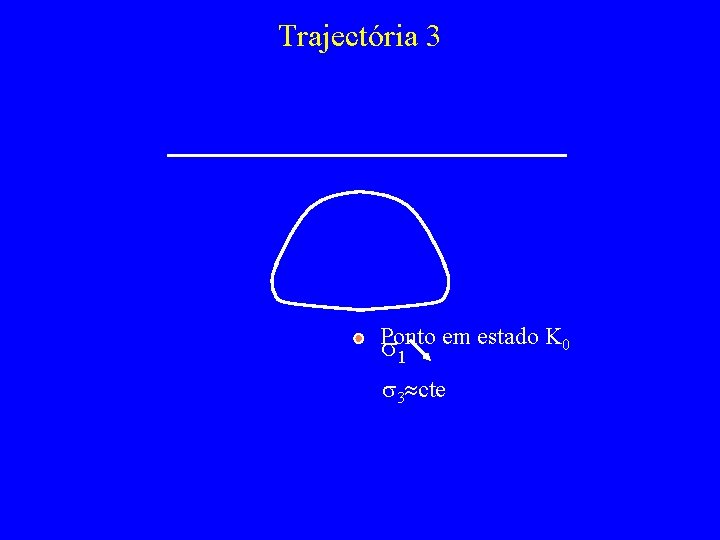
Trajectória 3 Ponto em estado K 0 s 1 s 3 cte

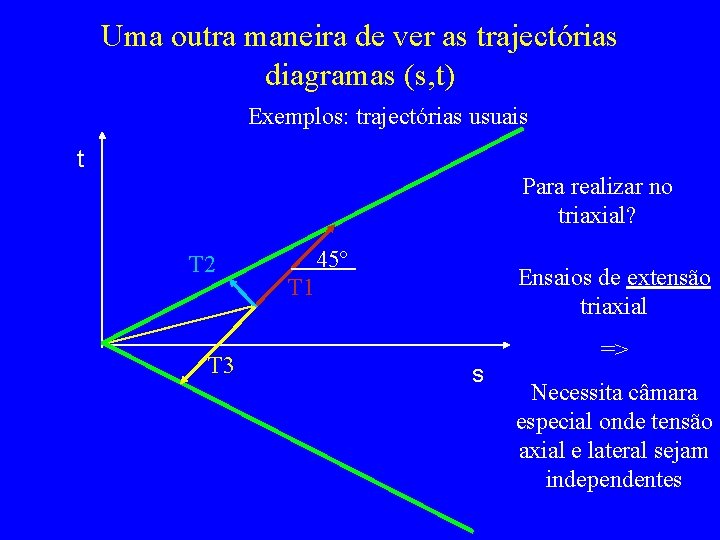
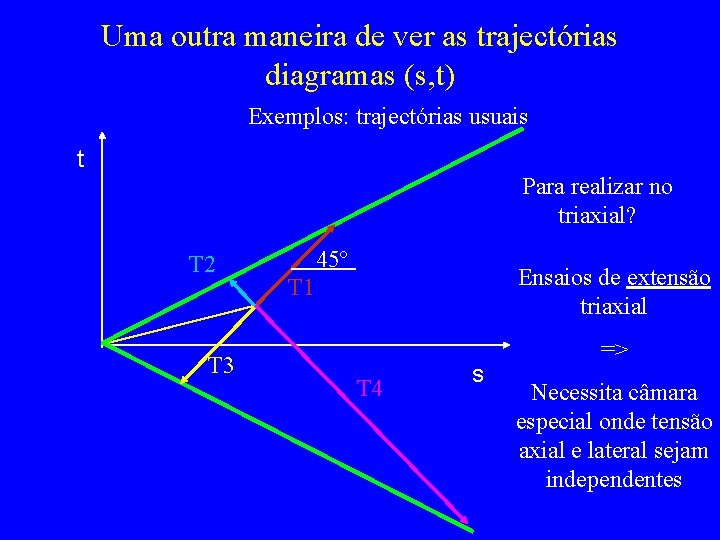
Uma outra maneira de ver as trajectórias diagramas (s, t) Exemplos: trajectórias usuais t Para realizar no triaxial? T 2 T 3 45º Ensaios de extensão triaxial T 1 s => Necessita câmara especial onde tensão axial e lateral sejam independentes

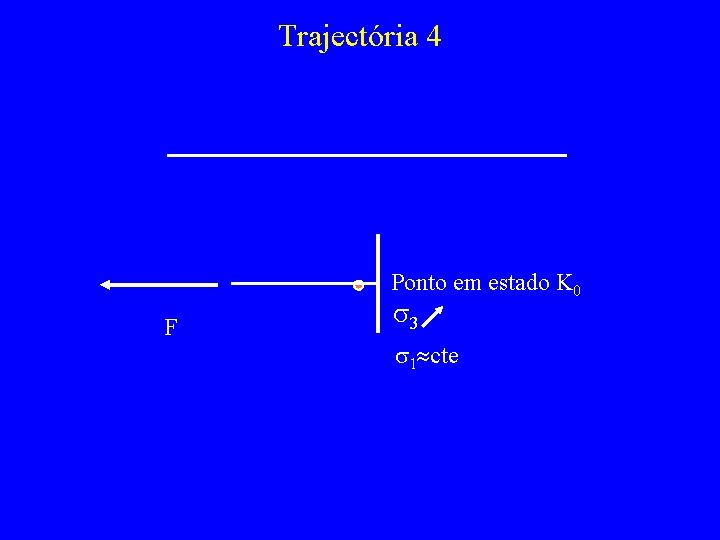
Trajectória 4 Ponto em estado K 0 F s 3 s 1 cte

Uma outra maneira de ver as trajectórias diagramas (s, t) Exemplos: trajectórias usuais t Para realizar no triaxial? T 2 T 3 45º Ensaios de extensão triaxial T 1 T 4 s => Necessita câmara especial onde tensão axial e lateral sejam independentes

Ensaios Triaxiais usuais (de compressão) è Ensaios – CID è Ensaios com Consolidação Isotrópica ou CIU (CD ou CU) com Consolidação Anisotrópica – CK 0 D ou CK 0 U

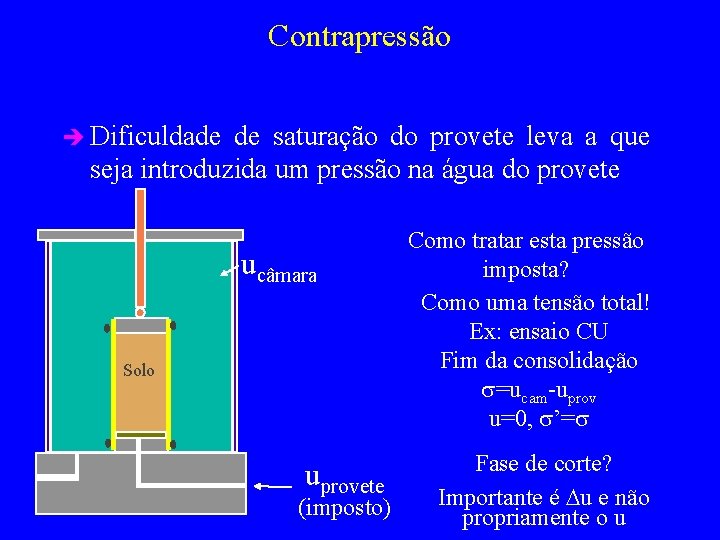
Contrapressão è Dificuldade de saturação do provete leva a que seja introduzida um pressão na água do provete ucâmara Solo uprovete (imposto) Como tratar esta pressão imposta? Como uma tensão total! Ex: ensaio CU Fim da consolidação s=ucam-uprov u=0, s’=s Fase de corte? Importante é Du e não propriamente o u

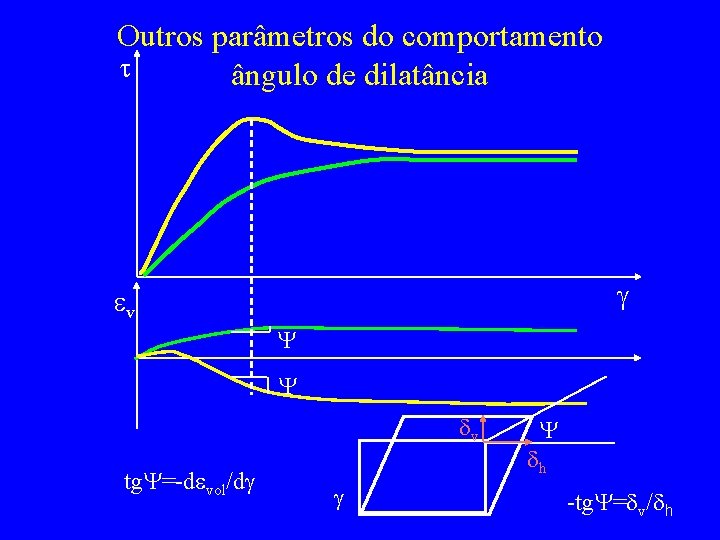
Outros parâmetros do comportamento t ângulo de dilatância g ev Y Y dv tg. Y=-devol/dg g Y dh -tg. Y=dv/dh

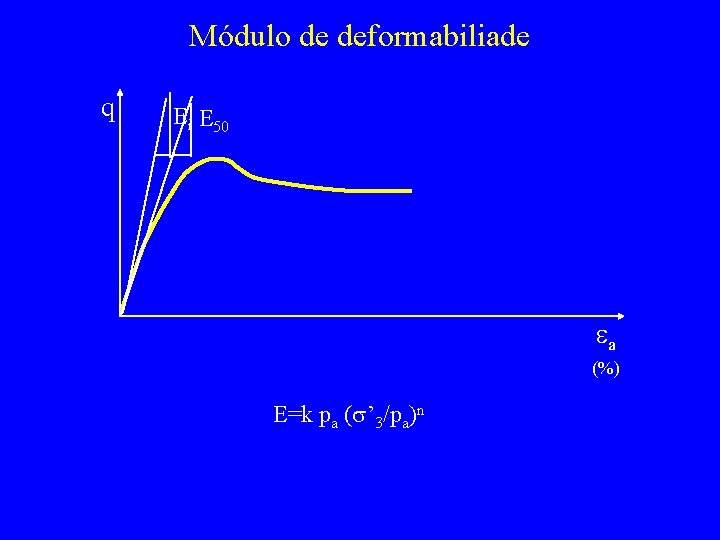
Módulo de deformabiliade q Ei E 50 ea (%) E=k pa (s’ 3/pa)n

ngulos de atrito de areias è Forma expedita de determinação
 Teoria coheso tenso transpiratoria
Teoria coheso tenso transpiratoria Corte transversal tubo seminifero
Corte transversal tubo seminifero Capsula externa
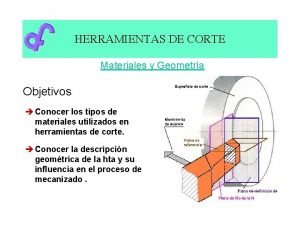
Capsula externa Herramientas de corte
Herramientas de corte Corte suprema funciones
Corte suprema funciones Atiesadores
Atiesadores Nbr 6492
Nbr 6492 Columna vertebral corte transversal
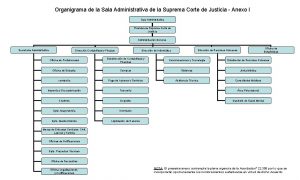
Columna vertebral corte transversal Suprema corte de justicia de la nacion organigrama
Suprema corte de justicia de la nacion organigrama Codigo ler taladrina
Codigo ler taladrina Corte histologico de corteza cerebral
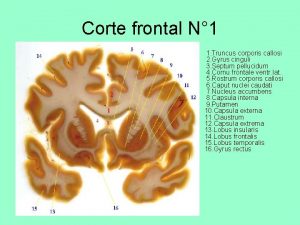
Corte histologico de corteza cerebral Sistema digestorio
Sistema digestorio Marco catalano corte dei conti
Marco catalano corte dei conti Secciones giradas
Secciones giradas Gade uca
Gade uca Corte sagital
Corte sagital Corte total
Corte total Corte transversal de la lana
Corte transversal de la lana Velocidade de corte
Velocidade de corte Corte transversal del mesencefalo
Corte transversal del mesencefalo Pictograma peinar
Pictograma peinar Concepto de cuento
Concepto de cuento Sentenze additive corte costituzionale
Sentenze additive corte costituzionale Corte penal internacional
Corte penal internacional Esfuerzos
Esfuerzos Corte axial
Corte axial Cunha geometria
Cunha geometria Puntos de corte en una funcion
Puntos de corte en una funcion Corte histológico
Corte histológico Lagrimal
Lagrimal Frecuencia de corte
Frecuencia de corte Tracto optico
Tracto optico Eminencia teres
Eminencia teres Imagenes del catorce de febrero
Imagenes del catorce de febrero Fibroblasto
Fibroblasto Cortes simples
Cortes simples Esfuerzo
Esfuerzo Corte total
Corte total Corte penal internacional función
Corte penal internacional función Configuracion externa del tronco encefalico
Configuracion externa del tronco encefalico Haplostela
Haplostela Sentenza corte costituzionale 215/87
Sentenza corte costituzionale 215/87 Poesia corte
Poesia corte Linha continua larga
Linha continua larga Genere di poesia epica
Genere di poesia epica Site:slidetodoc.com
Site:slidetodoc.com Catedral de pisa corte
Catedral de pisa corte Rogier de corte
Rogier de corte Ventana supraesternal
Ventana supraesternal Hialoplasma
Hialoplasma Horizontal
Horizontal Seudomonopolar
Seudomonopolar Respuesta
Respuesta Las chavetas trabajan al corte y al aplastamiento
Las chavetas trabajan al corte y al aplastamiento Karel de corte
Karel de corte Corte sifflet
Corte sifflet Fp corte y confeccion
Fp corte y confeccion Corte de alameda
Corte de alameda Herramientas de corte por aserrado
Herramientas de corte por aserrado Geometria de la herramienta de corte
Geometria de la herramienta de corte