Regressionsanalys Vi vill ha svar p frgan hur

Regressionsanalys • Vi vill ha svar på frågan hur mycket kommer y att förändras om x ändras med enhet. 1. Sambandets funktionsform 2. Tillåta att andra saker än x kan påverka y 3. Fånga upp ceteris paribus samband mellan y och x. 1

Regressionsanalys 1. Linjärt samband mellan y och x 2. ”Error term” inkluderas för att fånga upp att andra saker än x påverkar y 3. ”Zero conditional mean” antagandet möjliggör för oss att skatta ceteris paribus effekter. 2

Härledning av parametrar • Utgår från ”Zero Conditional Mean” antagandet 3

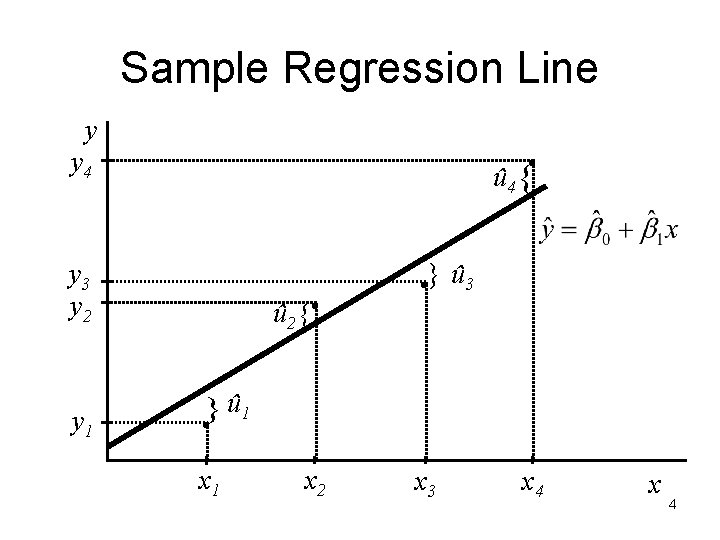
Sample Regression Line y . y 4 û 4 { y 3 y 2 y 1 û 2 {. . } û 3 û 1 }. x 1 x 2 x 3 x 4

Väntevärdesriktigt om… 1. populationsmodellen är linjär i parametrarna: y = b 0 + b 1 x + u 2. ett slumpmässigt urval av storleken n 3. E(u|x) = 0 och således E(ui|xi) = 0 4. det finns en variation i xi 5

Tolkning • Ekonomisk tolkning – 0: det förväntade värdet av y om x är lika med noll – 1: om x ökar med en enhet så ökar y med b enheter (mätt i samma enhet som y) 6

Exempel: Hedonisk Prisekvation • Priset på en fastighet är en funktion av de underliggande värdepåverkande attributen. • Sambandet mellan pris och attribut skattas mha regressionsanalys. • Estimerade parametrar är attributens implicita priser (hedoniska priser). 7

Den Hedoniska Prisekvationen • Fastighetsknutna egenskaper (F) • Områdesknutna egenskaper (O) • Tidsberoende egenskaper (T) 8

Exempel 9

Precision • Säkerheten hos modellen kan bl. a. mätas med hur stor spridningen i modellen är. Ju mindre spridning desto bättre modell. Spridningen mäts med variansen och standardavvikelsen. • Antar homoskedasticitet • Variansen hos a och b beror på modellens varians, antalet observationer samt medelvärdet och spridningen i den oberoende variabeln. 10

Precision • Standardfel hos skattningen av y • Standardfelet hos skattningarna b 0 och b 1 11

Modellen förklaringsgrad • Determinationskoefficienten, ”goodness of fit”, R-square, R 2 • SST: Total variation i den beroende variabeln • SSE: Variation som kan förklaras av modellen • SSR: Oförklarad variation • TSS=SSE+SSR • R 2=SSE/SST=1 -SSR/SST 12

Modellen förklaringsgrad • Determinationkoefficient (R 2) 13

Justerat R-Squared • R 2 ökar alltid ju fler variabler vi har med I modellen • Justerat R 2 tar hänsyn till detta genom att ställa antalet oberoende variabler i relation till antalet observationer 14

Exempel 15

Hypotestest • Kan vi dra några slutsatser angående populationen med hjälp av urvalet? • Till vår hjälp använder vi både lägesmått (medelvärdet) och spridning (standardavvikelsen). • Genom att skatta en teststorhet och jämför det mot ett kritiskt värde kan vi förkasta eller acceptera en hypotes. • Om förkastas, den oberoende variabeln har en inverkan. 16

Hypotestest Modell: Hypotes: y = a + b 1*x 1 + b 2*x 2 H 0: 1= 0 H 1: 1 0 Vi antar att parametrarna har en normalfördelning med det förväntade värdet och variansen 2 b, dvs b 1 N( 1, 2 b 1) Normalisera 17

Hypotestest Om, b 1 är okänd använder vi oss av skattningen av b 1 istället, vilket innebär att kvoten är t-fördelad istället för normalfördelad, dvs t är teststorheten tn-k-1 ( ) är det kritiska värdet Förkasta H 0 om t > tn-k ( ) 18

Hypotestest 19

Hypotestest • Om teststorheten är större än det kritiska värdet förkasta nollhypotesen. • Kritiskt värde (dubbelsidigt test): t /2 (n-k-1) – där är signifikansnivån och (n-k-1) antalet frihetsgrader. Vanligtvis använder man sig av signifikansnivån 5% och 1%. • Jmf. H 0: Ej begått mord – 5% chans att vi förkastar nollhypotesen att den åtalade ej begått mord, dvs vi dömer en oskyldig för mord. 20

Exempel 21

Funktionsform • Inte troligt att vi har ett linjärt samband mellan y och x i den meningen att y ökar med lika mycket oberoende hur mycket av x vi har initialt. • I tillämpade studier finner vi oftast att variablerna är transformerade, tex att alla kontinuerliga variabler är logaritmerade. Varför? – Vi vill att effekten skall uttryckas som en procentuell effekt. 22

Sammanfattning av olika funktionsformer • ln(y) = b 0 + b 1 ln(x) + u y ökar med b 1 procent om x ökar med 1 procent • ln(y) = b 0 + b 1 x + u y ökar med (100 b 1) procent om x ökar med 1 enhet • y = b 0 + b 1 ln(x) + u y ökar med (b 1/100) enheter om x ökar med 1 procent. 23

Dummyvariabel • En binär variabel som indikerar om en viss enskild observation (objekt) har en viss egenskap eller ej. • Om koefficientskattningen är signifikant skild från noll så innebär det att regressionsmodellen skiftar • Går att kombinera dummyvariabeln med kontinuerliga variabler. 24

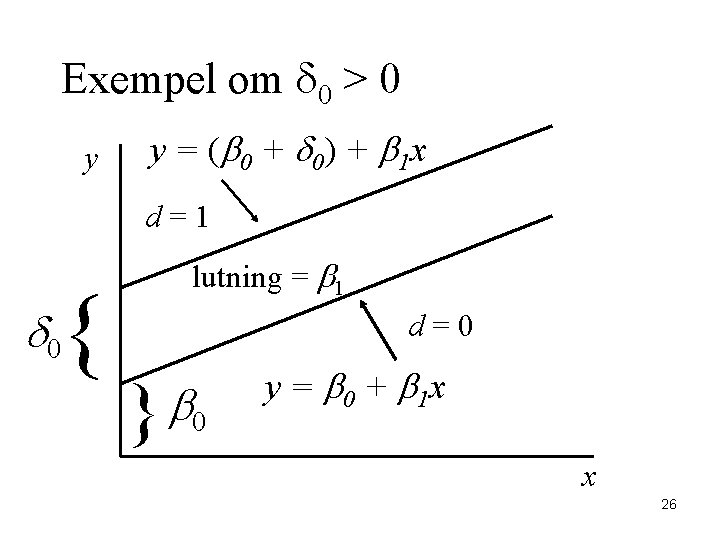
Dummy variabel som oberoende variabel • Antag en enkel modell där vi har en kontinuerlig variabel (x) och en dummy variabel (d) • y = b 0 + d 0 d + b 1 x + u • Kan tolkas som ett skift i konstanten • Om d = 0, y = b 0 + b 1 x + u • Om d = 1, y = (b 0 + d 0) + b 1 x + u 25

Exempel om d 0 > 0 y y = ( b 0 + d 0) + b 1 x d=1 { lutning = b 1 d 0 d=0 b } 0 y = b 0 + b 1 x x 26

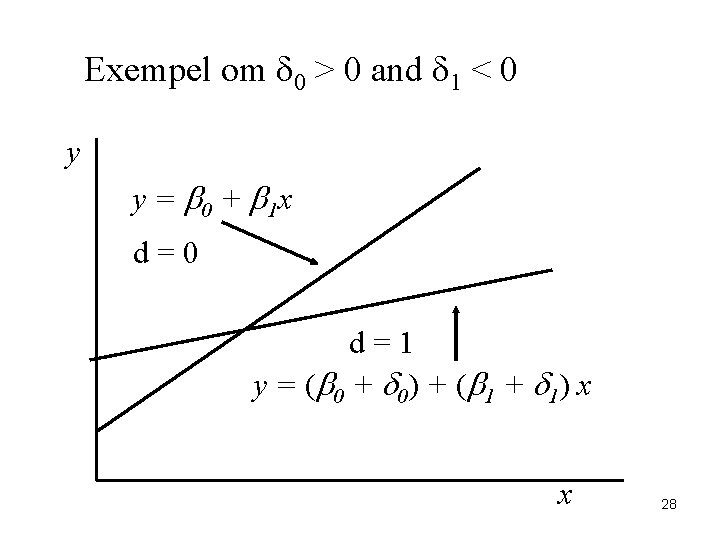
Interaktion med dummyvariabler • Man kan också kombinera en dummy variabel, d, med en kontinuerlig variabel, x • y = b 0 + d 1 d + b 1 x + d 2 d*x + u • Om d = 0, y = b 0 + b 1 x + u • Om d = 1, y = (b 0 + d 1) + (b 1+ d 2) x + u – Tolkas som om lutningen ändras 27

Exempel om d 0 > 0 and d 1 < 0 y y = b 0 + b 1 x d=0 d=1 y = (b 0 + d 0) + (b 1 + d 1) x x 28

Residualanalys

Varför bekymra sig för Heteroskedasticitet? • OLS ger fortfarande väntevärdesriktiga och konsistenta skattningar även om vi inte antar homoskedasticitet • MEN, standardavvikelsen avseende våra estimat är icke väntevärdesriktiga om vi har heteroskedasticitet • Om standardavvikelsen är icke väntevärdesriktig klan vi EJ genomföra våra hypotesprövningar. 30

Breusch-Pagan Test • Ett test som avser att undersöka om heteroskedasticitet förekommer eller ej. • Feltermen är okänd men vi har residualerna från OLS regressionen. • Om vi kör regressionen residualerna i kvadrat mot alla oberoende variabler så kan vi nyttja R 2 och göra ett F test • F-värdet anger om regressionsmodellen som helhet är statistiskt signifikant eller ej. • Ett ”högt” F-värde innebär att de oberoende variablerna kan förklara variationen i residualerna, vilket vi inte vill. • F = [R 2/k]/[(1 – R 2)/(n – k – 1)], 31 med fördelningen Fk, n – k – 1

Exempel 32

Exempel - test 33

Tidsserieanalys

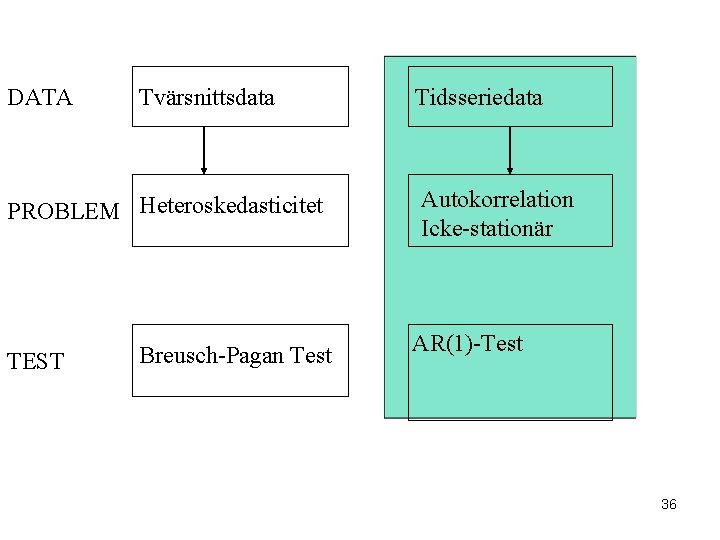
Tidsseriedata vs. Tvärsnittsdata • Tidsseriedata har en tidsordning till skillnad mot tvärsnittsdata. Det är av stor vikt att inte ändra ordningen. • Vi måste ha en modell som tillåter att historien kan påverka framtiden, men inte tvärtom. • Eftersom vi har data som är ordnande i tiden måste vi lägga till antaganden om hur feltermen (residualen) får bete sig över tiden. 35

DATA Tvärsnittsdata PROBLEM Heteroskedasticitet TEST Breusch-Pagan Test Tidsseriedata Autokorrelation Icke-stationär AR(1)-Test 36

Exempel på tidsseriedata modeller • En statisk modell där variablerna påverkar y direkt: yt = b 0 + b 1 zt + ut • En laggad (dynamisk) modell tillåter att en eller flera variabler påverka y med en lag: yt = a 0 + d 0 zt + d 1 zt-1 + d 2 zt-2 + ut 37

Statisk Modell FPIt = b 0 + b 1 BNPIt + ut OBS! INDEX Tolkning: Procentenhet 38

Tolkning • FPI och BNP är index med 1967=100 • Ekonomisk tolkning – om BNP gick upp med en procentenhet föregående år så kommer FPI att gå upp med 0. 69 procentenheter. • Statistisk tolkning – modellens förklaringsgrad, genomsnittligt fel, statistisk signifikans av enskilda parametrar. 39

Statisk Modell Ln(FPIt) = b 0 + b 1 l(BNPIt) + ut Tolkning: Procent 40

Dynamisk modell Ln(FPIt )= b 0 + b 1 Ln(BNPt-1) + ut Tolkning: Procent 41

Antaganden 1. Linjär i parametrarna 2. Det förväntade värdet av feltermen betingat på den oberoende variabeln skall vara lika med noll. X strikt exogena 3. Ej perfekt linjärt samband mellan oberoende variabler 4. Homoskedasticitet NYTT! 5. Ingen autokorrelation 6. Normalfördelning 42

OLS skattningarnas varians • Homoskedasticitet – Var(ut|X) = Var(ut) = s 2 • Variansen är oberoende av alla x samt konstant över tiden • Ingen autokorrelation: – Corr(ut, us| X)=0 for t s 43

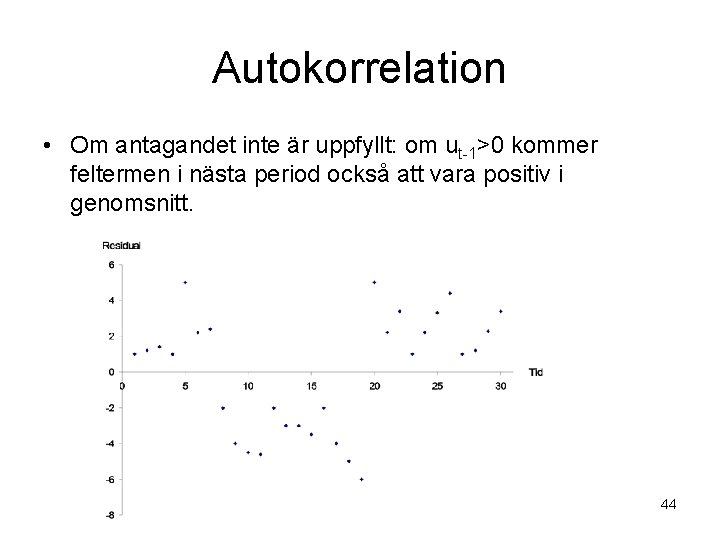
Autokorrelation • Om antagandet inte är uppfyllt: om ut-1>0 kommer feltermen i nästa period också att vara positiv i genomsnitt. 44

Varför problem? • Effektivitet – det finns andra metoder än OLS som ger mer effektiva skattningar, dvs med lägre varians. Dock är OLS parameterskattningar väntevärdesriktiga. • Hypotesprövning – variansen är inte väntevärdesriktig vilket innebär att hypotesprövning och konfidensintervall inte längre är tillförlitliga. 45

Hur testa för autokorrelation? • AR(1)-test • AR(1) = Autoregressive modell där den beroende variabeln är en funktion av den beroende variabeln laggad 1 år. yt = ryt-1 + et , t = 1, 2, … • Test av AR(1) autokorrelation • Vi vill testa nollhypotesen r = 0 i ut = rut-1 + et, t =2, …, n • Om ej förkasta H 0 (lågt t-värde) ingen autokorrelation 46

Exempel – Dynamisk modell Autoregressive modell Residualen idag är en funktion av residualen igår. Om signifikant parameter-autokorrelation. 47

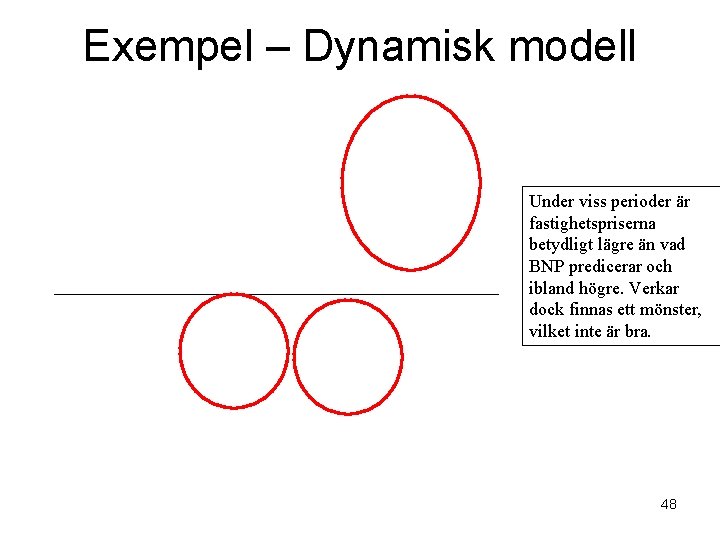
Exempel – Dynamisk modell Under viss perioder är fastighetspriserna betydligt lägre än vad BNP predicerar och ibland högre. Verkar dock finnas ett mönster, vilket inte är bra. 48

Orsaker? • Tröghet – tidsseriedata, av psykologiska skäl har historiska händelser en stor effekt på dagens händelser så att ett positivt fel i föregående period påverkar aktiviteten idag. • Långsiktigheten – tidsseriedata, en slumpmässig chock på en marknad kan ha långsiktiga effekter, tex krig. • Specifikationsfel – val av ingående variabler, funktionsform. 49

Fel funktionsform 50

Vad göra? • Fler förklarande variabler (t. ex. i vårt fall en dummyvariabel som indikerar bankkrisen mellan 1991 -96). • Andra funktionsformer – Log-log – Nivå-log – Log-nivå • Första-differensen – förändringsdata istället för nivådata 51

Trendade tidsserier • Ekonomiska tidsserier har ofta en trend. • Bara för att två serier är trendade tillsammans kan vi inte anta att det finns ett kausalt samband. • Oftast är serierna trendade för att det finns någon icke-observerbar faktor som är gemensam, men som inte är inkluderad i modellen. • Även om dessa faktorer är icke-observerade kan vi kontrollera för dem genom att direkt inkludera en trend i våran modell. 52

Inkludera trend i modellen • En möjlighet är en linjär trend yt = a 0 + a 1 t + et, t = 1, 2, … • En annan är en exponentiell trend log(yt) = a 0 + a 1 t + et, t = 1, 2, … • Eller en kvadratisk trend yt = a 0 + a 1 t + a 2 t 2 + et, t = 1, 2, … 53

Varför problem? • Uppfyller inte antagande nr. 2 – Det förväntade värdet av feltermen betingat av våra oberoende variabler är inte lika med noll. X är inte exogent given. • DVS våra parameterskattningar avseende intercept (konstant) och lutningskoefficient är inte väntevärdesriktig. • Kan ej göra vare sig ekonomisk eller statistisk tolkning av skattningarna. • DVS vi kan inte tolka i termer av ceteris paribus (allt annat lika). 54

Stationära serier • En trendad serie kallas för icke-stationär eftersom medelvärdet förändras med tiden. • En enkel regression med yt som beroende variabel och xt som oberoende variabel och båda är icke-stationära innebär att t-värdena kommer ofta att vara signifikanta även om det inte finns ett samband. Vanligtvis också ett högt R 2. • Kallas för “spurious regression problem” 55

Transformera serien • Om det inte räcker med att inkludera en trend i specifikationen av modellen utan vi fortfarande har en icke-stationär serie måste vi transformera serien. • Oftast räcker det med att använda sig av förstadifferensen för att få en stationär serie. 56

Prognos och Utvärdering av Prognos

Prognosmodell • Tidsseriedatamodeller används vanligt som prognosmodell vid sidan om förklaringsmodeller. • Viktigt att vi därför utvärderar dess prognosegenskaper. • Problem med att endast analysera koefficienter, t -värden och modellens förklaringsgrad då dessa bygger på ”in-sample” prognoser (skattningar). • En mer realistisk situation är att utvärdera modellen utifrån dess ”out-of-sample” prognoser. 58

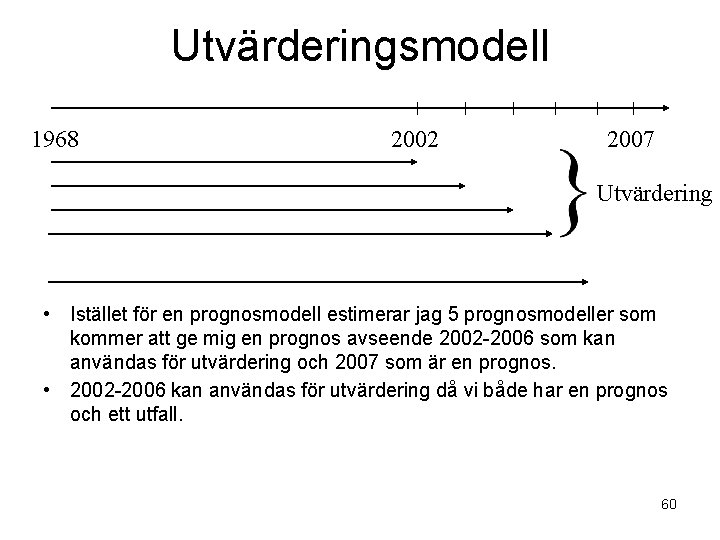
Prognosmodell med utvärdering • Anta att vi har data från 1968 -2006. • Antag att vi vill förklara prisutvecklingen på småhus med hjälp av BNP-utvecklingen (laggad 1 år). • Genom att använda hela datamängden kan vi göra prognos avseende 2007. • I och för sig får vi en skattad pris för hela perioden men det är en ”in-sample” prognos. • Genom att beräkna ett antal prognosmodeller med olika datamängd så kan vi göra ”out-ofsample” prognoser. 59

Utvärderingsmodell 1968 2002 2007 Utvärdering • Istället för en prognosmodell estimerar jag 5 prognosmodeller som kommer att ge mig en prognos avseende 2002 -2006 som kan användas för utvärdering och 2007 som är en prognos. • 2002 -2006 kan användas för utvärdering då vi både har en prognos och ett utfall. 60

Jämförelse • För att kunna jämföra min prognosmodell med något så tar jag fram ett antal jämförelseprognoser. • Det kan tex vara andra prognosmodeller med andra variabler, med annan laggning eller funktionsform. • Det kan också utgöras av betydligt enklare prognoser som tex – Samma utveckling nästa år som i år – Glidande medelvärde – Autoregressive modell tex AR(1) 61

Mått på genomsnittligt prognosfel Det genomsnittliga prognosfelet uppgår till 25 procentenheter per år. 62

Långa prognoser • Betydligt svårare • Om vi vill göra en längre prognos än ett år måste vi lägga in antaganden om BNP-utvecklingen (eftersom modellen är laggad med bara ett år). • Naturligtvis kan man själv göra en prognosmodell avseende BNP och andra makroekonomiska variabler eller • Så kan man använda de prognoser som tex Konjunkturinstitutet tar fram. • Tolkningen blir då betingat av KIs prognos. 63