Razes e otimizao Renato Assuno DCC UFMG Razes

Raízes e otimização Renato Assunção DCC, UFMG

Raízes de equações �Um tipo de problema bastante comum é o de achar raízes de equações da forma f(x) = 0, onde f(x) pode ser um polinômio ou uma função transcendental �O valor de x que satisfaz f(x) = 0 é chamada de raiz da equação. �Raramente podemos obter as raízes de tais funções de modo exato. �Vários procedimentos fornecem métodos para calcular uma seqüência de aproximações, que convergem para uma solução tão precisa quanto necessária, resguardadas algumas condições

De funções relativamente simples. . . �Polinômios e �combinações finitas de funções �transcendentais �Fácil de plotar. �f(x)=3*sin(x 2) + e-x - (x-3)2 + 4*x

. . . a funções mais complexas �Achar a primeira raiz positiva da função de Bessel de primeira ordem (solução de certas equações diferenciais ordinárias)

Outro problema: maximização �Maximar uma função: otimização de recursos. �No fundo, problema pode ser reduzido a encontrar a raiz de uma função. �Achar Maxx f(x) �E’ equivalente a achar a raiz da função derivada �f ‘(x) = 0 �Assim, maximizar reduz-se a achar raízes de equações não-lineares.

Sistemas de equações não-lineares

Sistema de equações não-lineares Equação do míssil Equação do interceptador

O que vamos cobrir �Vamos estudar apenas UMA ÚNICA FUNCAO NÃO_LINEAR f(x) �Não vamos estudar sistemas de equações não-lineares

Um teorema que dispensa prova �Antes de examinarmos vários métodos para determinar raízes isoladas de f(x) = 0, vamos ver o teorema abaixo e alguns exemplos �Teorema: Suponha que uma função contínua f(x) assume valores de sinais opostos nos pontos extremos do intervalo [a, b]. �Isto é, suponha que f(a) * f(b) < 0 �Então existe pelo menos um ponto x’ ∈[a, b], tal que f(x’) = 0 �Isto e’, existe uma raiz entre a e b.

Exemplos �Vamos examinar o comportamento das �funções f(x)= ln(c xp ) e f(x)= e(x)

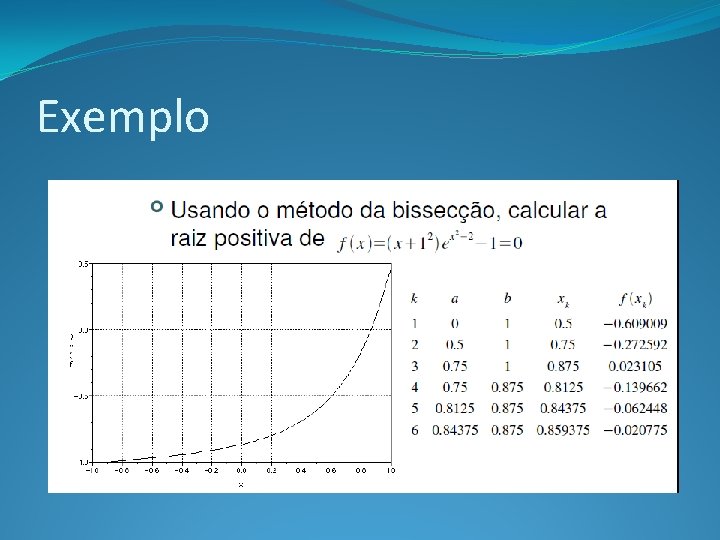
Método da Bissecção �Considere o intervalo [a, b] para o qual f(a) * f(b) < 0. �No método da bissecção nós calculamos o valor da função f(x) no ponto médio x 1 = (a + b)/2 �Caso f(x) =0, x 1 é a raiz procurada e o processo para. �Se f(a) * f(x 1) < 0, a raiz procurada está entre a e x 1, e repete-se o processo para o intervalo [a, x 1]. �Caso contrário, f(x 1) * f(b) < 0, e a raiz procurada está entre x 1 e b. Logo, repete-se o processo para o intervalo [x 1, b]

Método da Bissecção

e’ a raiz procurada

Precisão e parada: cuidados

Precisão e parada: cuidados

Falta ainda o limite maximo do numero de iterações. Se atingido, enviar uma mensagem de warning: limite atingido

Exemplo

Vantagens e desvantagens

Método de Newton

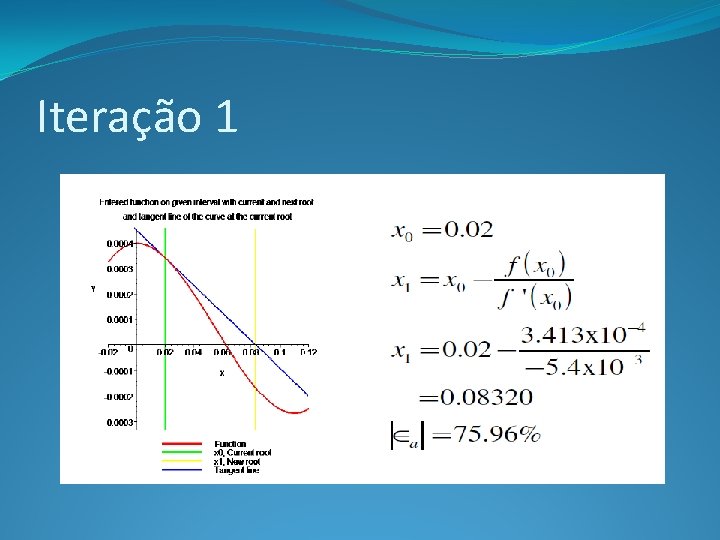
Iteração 1

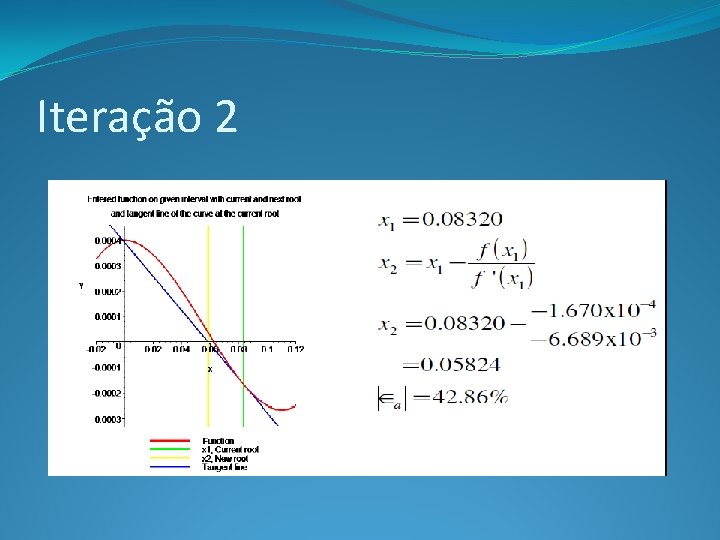
Iteração 2

Iteração 3

Vantagens

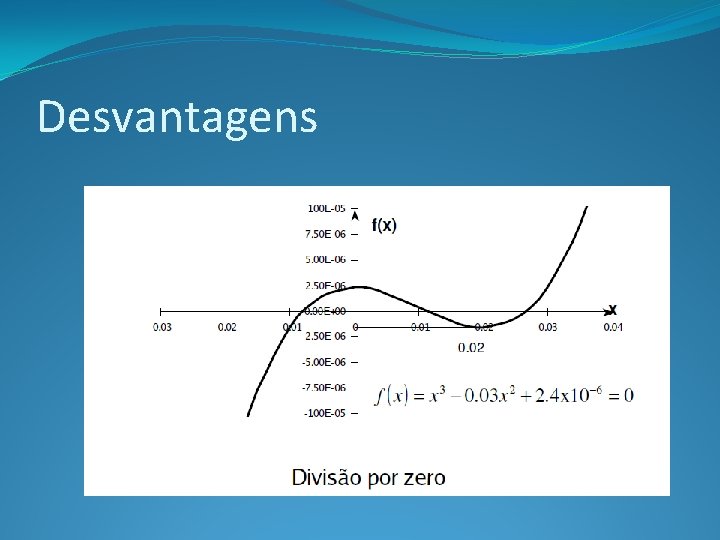
Desvantagens

Método das secantes

Ilustração – método das secantes

Metodo Regula Falsi

Ordem de convergência