POLE FIGURY Miara Jordana Pole figury Miara Jordana



























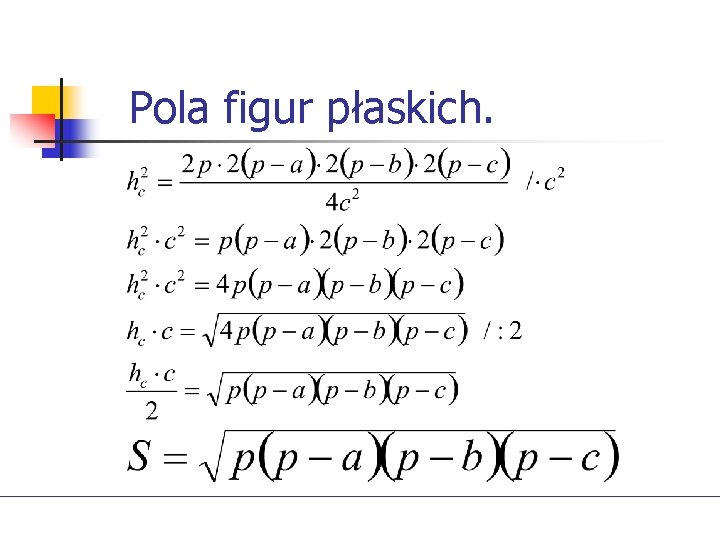
- Slides: 36

POLE FIGURY Miara Jordana

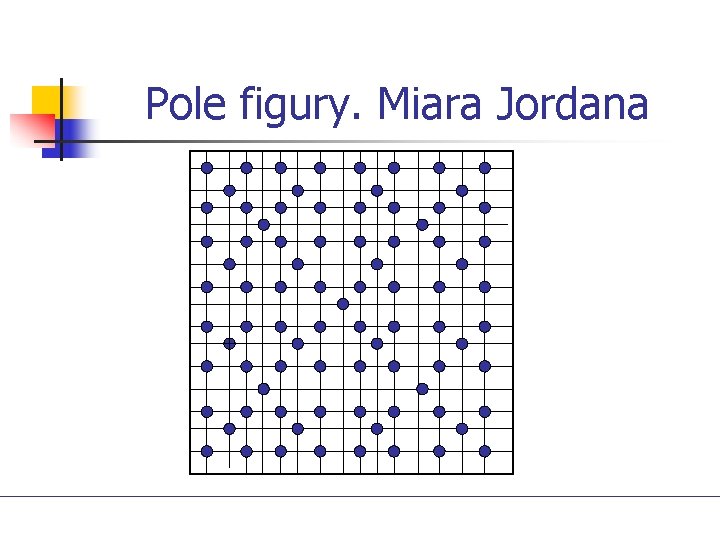
Pole figury. Miara Jordana Pokryjmy płaszczyznę kwadratami o boku długości 1 w sposób przedstawiony na rysunku:

Pole figury. Miara Jordana Zbiór wszystkich kwadratów nazywamy SIECIĄ ZEROWĄ i oznaczamy K 0. Pole pojedynczego kwadratu jest równe: P 0=1

Pole figury. Miara Jordana Podzielmy każdy bok kwadratu „na pół” tworząc nową sieć K 1. Pole pojedynczego kwadratu jest równe: P 1=1/4

Pole figury. Miara Jordana Postępując analogicznie tworzymy kolejne sieci K 2 , K 3 , K 4 , …, Kn , … o polach P 2= 1/16 = 1/24 P 3= 1/64 = 1/26 … Pn= 1/22 n. . .

Pole figury. Miara Jordana Weźmy dowolną figurę F i nałóżmy na nią sieć K 0

Pole figury. Miara Jordana Następnie wyznaczamy liczbę kwadratów zawartych w figurze F i obliczmy ich pole. (U nas liczba kwadratów – 2 i ich pole = 2) Oznaczmy to pole przez W 0 Wyznaczamy liczbę kwadratów pokrywających figurę F są to te kwadraty, które mają chociaż jeden punkt wspólny. (U nas liczba kwadratów – 14 i ich pole = 14) Oznaczmy to pole przez Z 0

Pole figury. Miara Jordana Następnie na figurę F nałóżmy sieć K 1

Pole figury. Miara Jordana Następnie wyznaczamy liczbę kwadratów zawartych w figurze F i obliczmy ich pole. (U nas liczba kwadratów – 16 i ich pole = 4) Oznaczmy to pole przez W 1 Wyznaczamy liczbę kwadratów pokrywających figurę F są to te kwadraty, które mają chociaż jeden punkt wspólny. (U nas liczba kwadratów – 41 i ich pole = 10, 25) Oznaczmy to pole przez Z 1

Pole figury. Miara Jordana Następnie na figurę F nałóżmy sieć K 2

Pole figury. Miara Jordana Następnie wyznaczamy liczbę kwadratów zawartych w figurze F i obliczmy ich pole. (U nas liczba kwadratów – 85 i ich pole = 5, 3125) Oznaczmy to pole przez W 2 Wyznaczamy liczbę kwadratów pokrywających figurę F są to te kwadraty, które mają chociaż jeden punkt wspólny. (U nas liczba kwadratów – 130 i ich pole = 8, 125) Oznaczmy to pole przez Z 2

Pole figury. Miara Jordana Nakładamy na figurę F kolejne sieci i wyznaczamy pola W 3 , W 4 , …, Wn , … i Z 3 , Z 4 , …, Zn , … , Otrzymujemy dwa ciągi

Pole figury. Miara Jordana Zauważmy, że zachodzi tzn. ciąg a ciąg jest rosnący i ograniczony z góry jest malejący i ograniczony z dołu

Pole figury. Miara Jordana Na mocy twierdzenia (z teorii granic ciągów liczbowych) ciągi monotoniczne i ograniczone są zbieżne (tzn. mają granice). Zatem ciągi są zbieżne (mają granice).

Pole figury. Miara Jordana Granicę figury F. nazywamy miarą wewnętrzną Granicę figury F. nazywamy miarą zewnętrzną

Pole figury. Miara Jordana Definicja Mówimy, że figura F jest mierzalna (ma pole) jeżeli miara wewnętrzna jest równa mierze zewnętrznej: W(F)=Z(F)=m(F) Liczbę m(F) nazywamy miarą (polem) figury F.

Pole figury. Miara Jordana WŁASNOŚCI MIARY (POLA) : 1. Pole figury jest liczbą nieujemną tj. 2. Figury przystające mają równe pola tj.

Pole figury. Miara Jordana 3. Figura będąca sumą dwóch figur nie mających wspólnych punktów wewnętrznych ma pole równe. sumie pól figur składowych: 4. Jeżeli figury F 1 i F 2 mają pola i figura to

Pole figury. Miara Jordana 5. Pole prostokąta o bokach a i b jest równe P=ab. 6. Figura „jednowymiarowa” ma pole równe 0 (punkt, odcinek, łuk krzywej itd. )

Pole figury. Miara Jordana Przykład figury niemierzalnej (bez pola) 1. Kwadrat-sito Weźmy kwadrat o boku długości 1. Dzielimy go na 4 przystające kwadraty i „wyrzucamy” ich punkt wspólny. Następnie każdy z powstałych kwadratów ponownie dzielimy na 4 przystające kwadraty i „wyrzucamy” ich punkty wspólne. Itd…

Pole figury. Miara Jordana

Pole figury. Miara Jordana Zauważmy, że miara wewnętrzna W(F)=0 miera zewnętrzna Z(F)=1 zatem figura nie jest mierzalna!

Pole figury. Miara Jordana 2. Dywan Sierpińskiego Weźmy kwadrat o boku długości 1. Dzielimy go na 9 przystających kwadratów i „wyrzucamy” środkowy. Następnie każdy z powstałych kwadratów ponownie dzielimy na 9 przystających kwadratów i „wyrzucamy” środkowy. Itd…

Pole figury. Miara Jordana

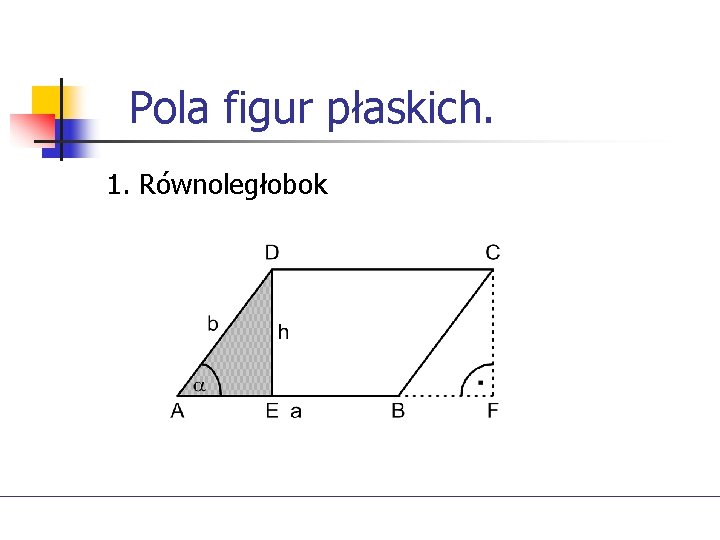
Pola figur płaskich. 1. Równoległobok

Pola figur płaskich.

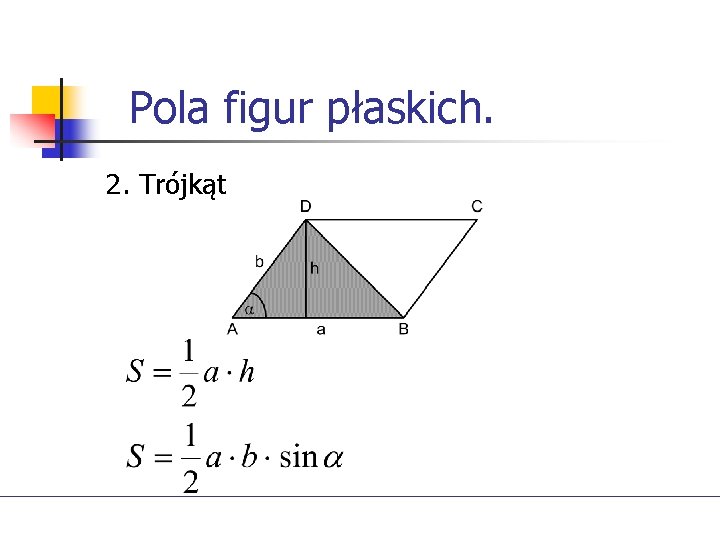
Pola figur płaskich. 2. Trójkąt

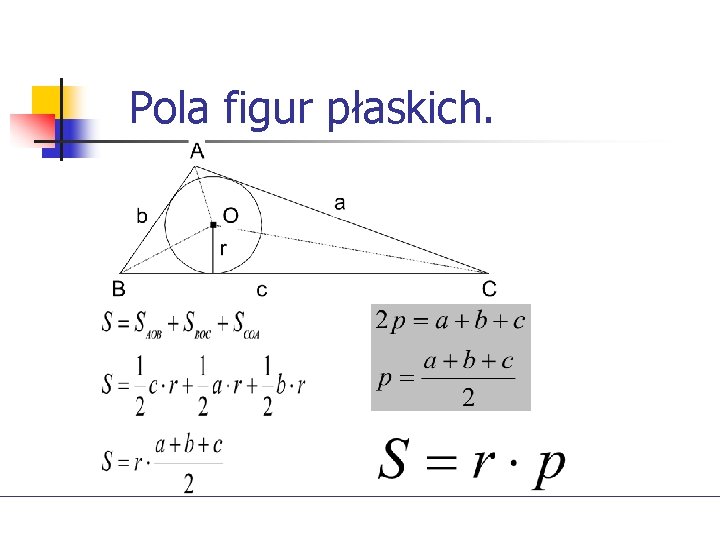
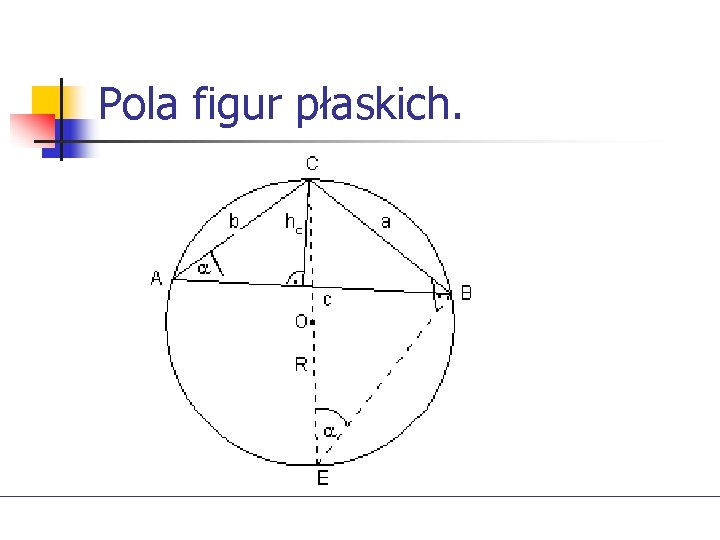
Pola figur płaskich.

Pola figur płaskich.

Pola figur płaskich.

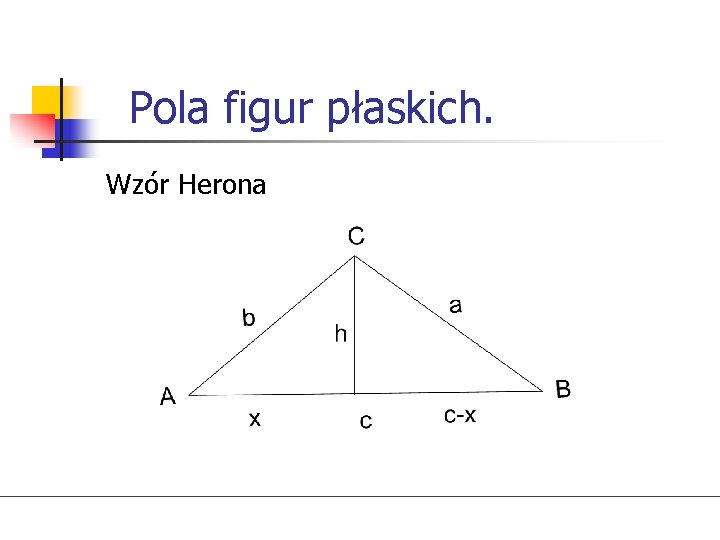
Pola figur płaskich. Wzór Herona

Pola figur płaskich. Z twierdzenia Pitagorasa Po odjęciu stronami otrzymamy

Pola figur płaskich. Po wstawieniu x do I równania, zastosowaniu wzorów skróconego mnożenia oraz podstawieniu i „prostych” rachunkach otrzymamy:
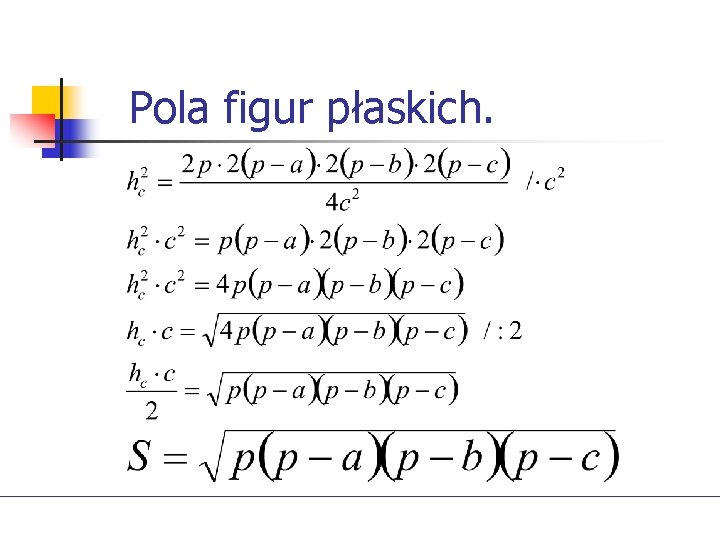
Pola figur płaskich.

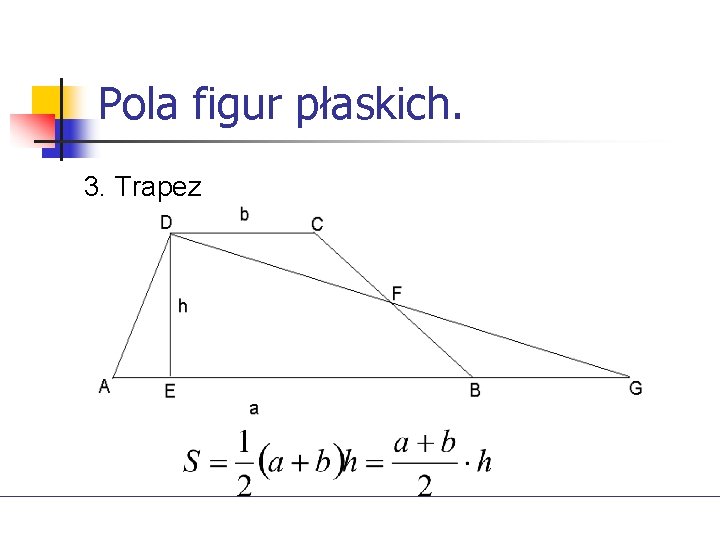
Pola figur płaskich. 3. Trapez

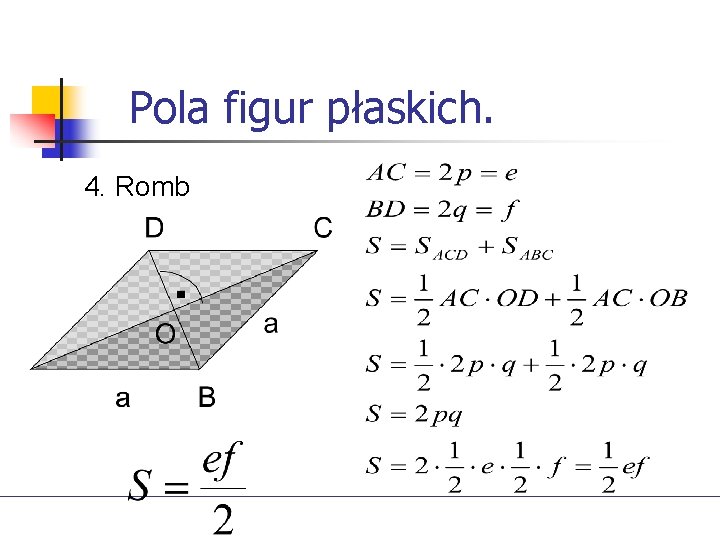
Pola figur płaskich. 4. Romb
 Pole figury definicja
Pole figury definicja Oblicz pole i obwód figur
Oblicz pole i obwód figur Oblicz pole i obwód figury przedstawionej na rysunku
Oblicz pole i obwód figury przedstawionej na rysunku Katherine duer mackay
Katherine duer mackay Poco jordana
Poco jordana Solidificação
Solidificação Difference between lap winding and wave winding
Difference between lap winding and wave winding Define north pole and south pole
Define north pole and south pole Aimant pole nord pole sud
Aimant pole nord pole sud Co jest miarą oddziaływań
Co jest miarą oddziaływań Stopa miara
Stopa miara Rumb dla geodety
Rumb dla geodety Kowariancja wzór
Kowariancja wzór Staropolska miara długości tkaniny
Staropolska miara długości tkaniny Stopa miara
Stopa miara Slávnostný prejav stužková
Slávnostný prejav stužková Atmosférická perspektiva
Atmosférická perspektiva Na rysunku przedstawiono kwadraty abcd eaod
Na rysunku przedstawiono kwadraty abcd eaod štědrý den (kytice (rozbor))
štědrý den (kytice (rozbor)) Rzut figury na płaszczyznę
Rzut figury na płaszczyznę Tworząca stożka
Tworząca stożka Figura przestrzenna wielościan
Figura przestrzenna wielościan Ostrosłup sześciokątny
Ostrosłup sześciokątny Cecha figur nieforemnych
Cecha figur nieforemnych Które figury łączy w sobie hetman?
Które figury łączy w sobie hetman? Kółka stanowią 20 wszystkich figur
Kółka stanowią 20 wszystkich figur Figury osiowosymetryczne definicja
Figury osiowosymetryczne definicja Złudzenie ponzo
Złudzenie ponzo Dziewięciokąt foremny
Dziewięciokąt foremny Znele spoluhlasky
Znele spoluhlasky Figury geometryczne z półosiami
Figury geometryczne z półosiami Symetria prezentacja
Symetria prezentacja Figury geometryczne - prezentacja
Figury geometryczne - prezentacja Figury o czterech bokach to
Figury o czterech bokach to Podstawowe figury geometryczne
Podstawowe figury geometryczne Hyperbola literatura
Hyperbola literatura Srodkowa trapezu
Srodkowa trapezu