Physics Beyond 2000 Chapter 1 Kinematics Physical Quantities

Physics Beyond 2000 Chapter 1 Kinematics

Physical Quantities • Fundamental quantities • Derived quantities
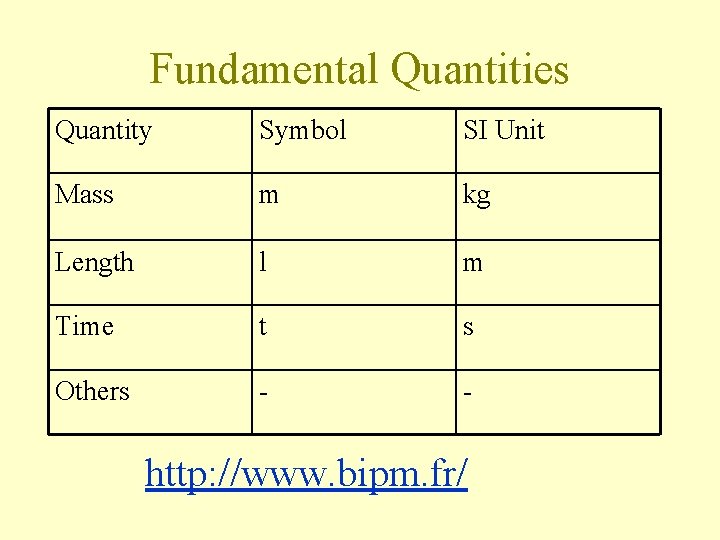
Fundamental Quantities Quantity Symbol SI Unit Mass m kg Length l m Time t s Others - - http: //www. bipm. fr/

Derived Quantities • Can be expressed in terms of the basic quantities • Examples – Velocity – Example 1 – Any suggestions?

Derived Quantities • More examples

Standard Prefixes • Use prefixes for large and small numbers • Table 1 -3 • Commonly used prefixes – giga, mega, kilo – centi, milli, micro, nana, pico

Significant Figures The number of digits between the Most significant figure and least significant figure inclusive. • The leftmost non-zero digit is the most significant figure. • If there is no decimal point, the rightmost non-zero digit will be the least significant figure. • If there is a decimal point, the rightmost digit is always the least significant figure.

Scientific Notation • Can indicate the number of significant numbers

Significant Figures • Examples 5 and 6. • See if you understand them.

Significant Figures • Multiplication or division. – The least number of significant figures. • Addition or subtraction. – The smallest number of significant digits on the right side of the decimal point.

Order of Magnitude • Table 1 -4.

Measurement • Length – Meter rule – Vernier caliper – Micrometer screw gauge Practice

Measurement • Time interval – Stop watch – Ticker tape timer – Timer scaler

Measurement • Mass – Triple beam balance – Electronic balance

Measurement • Computer data logging

Error Treatment • Personal errors – Personal bias • Random errors – Poor sensitivity of the apparatus • System errors – Measuring instruments – Techniques

Accuracy and Precision • Accuracy – How close the measurement to the true value Precision – Agreement among repeated measurements – Largest probable error tells the precision of the measurement

Accuracy and Precision • Examples 9 and 10

Accuracy and Precision • Sum and difference – The largest probable error is the sum of the probable errors of all the quantities. – Example 11

Accuracy and Precision • Product, quotient and power – Derivatives needed

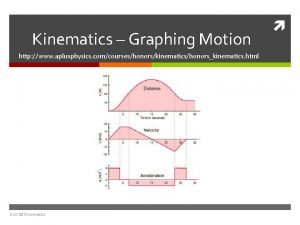
Kinematics • Distance d • Displacement s
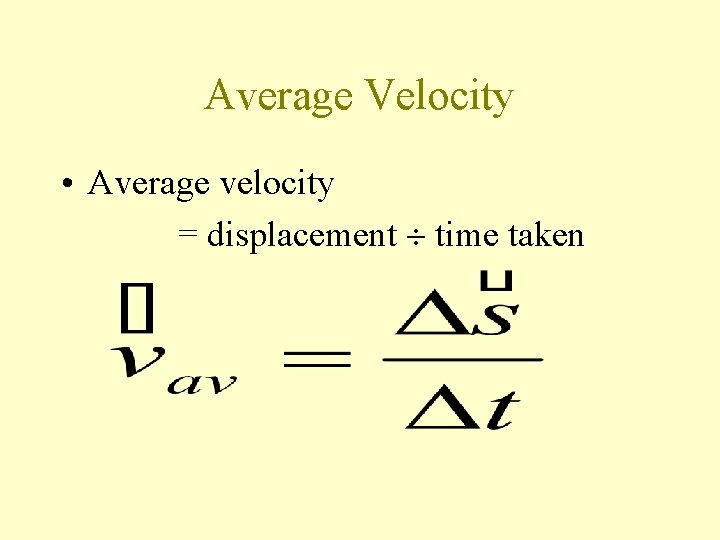
Average Velocity • Average velocity = displacement time taken

Instantaneous Velocity • Rate of change of displacement in a very short time interval.

Uniform Velocity • Average velocity = Instantaneous velocity when the velocity is uniform.

Speed • Average speed • Instantaneous speed

Speed and Velocity • Example 13

Relative Velocity • The velocity of A relative to B • The velocity of B relative to A

Relative Velocity • Example 14

Acceleration • Average acceleration • Instantaneous acceleration

Average acceleration • Average acceleration = change in velocity time Example 15

Instantaneous acceleration Example 16
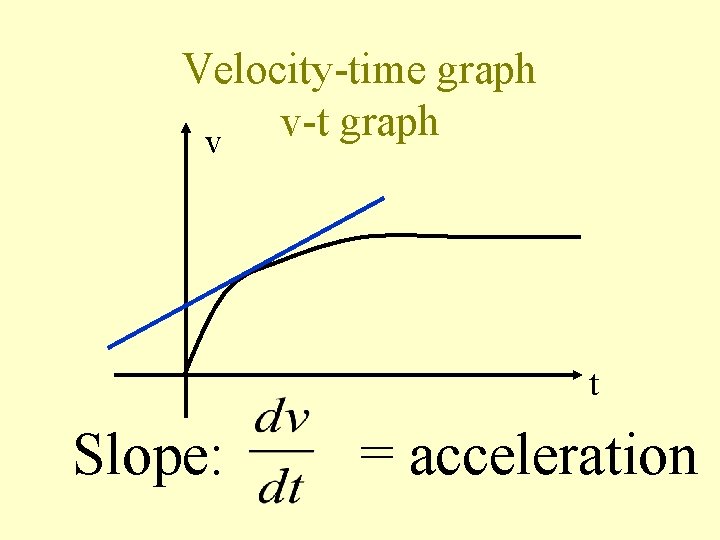
Velocity-time graph v-t graph v t Slope: = acceleration
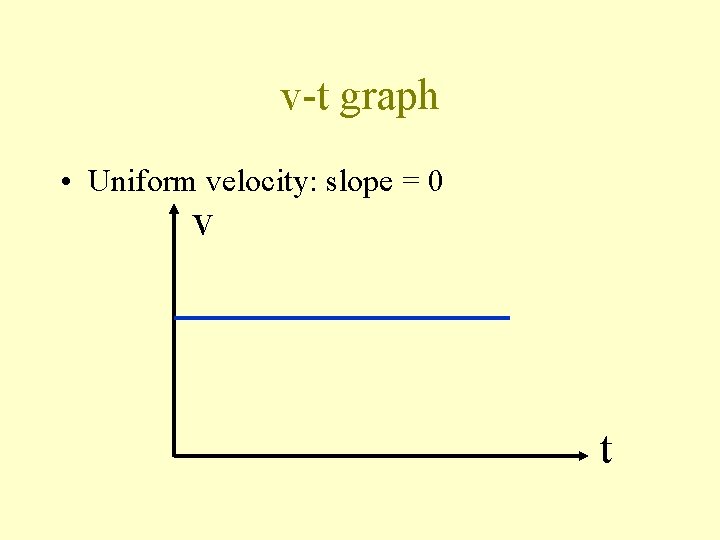
v-t graph • Uniform velocity: slope = 0 v t
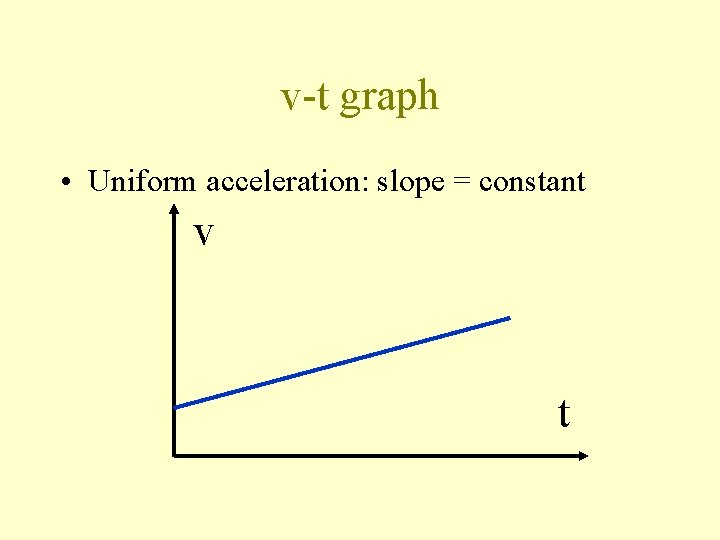
v-t graph • Uniform acceleration: slope = constant v t
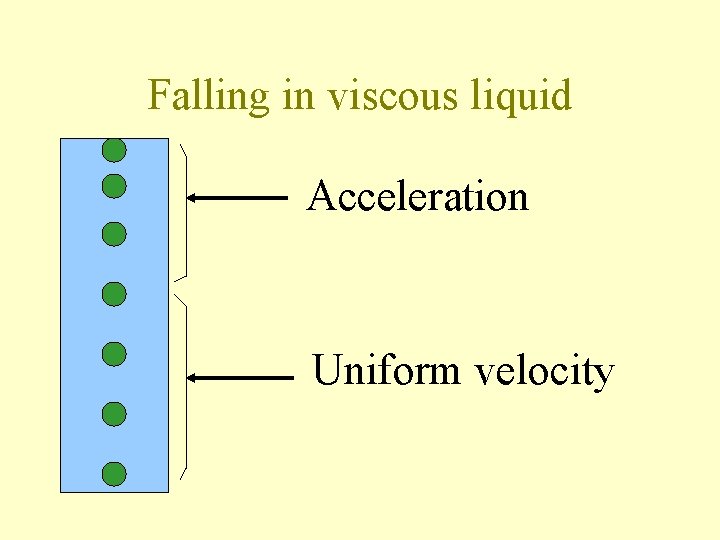
Falling in viscous liquid Acceleration Uniform velocity
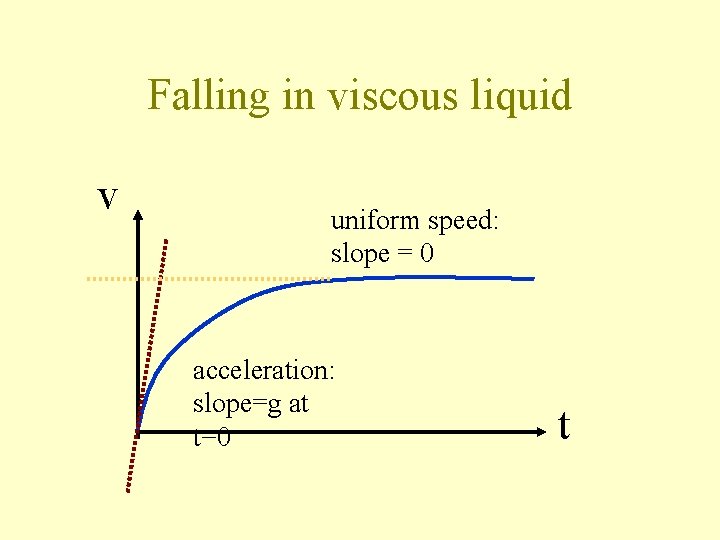
Falling in viscous liquid v uniform speed: slope = 0 acceleration: slope=g at t=0 t

Bouncing ball with energy loss Let upward vector quantities be positive. Falling: with uniform acceleration a = -g.
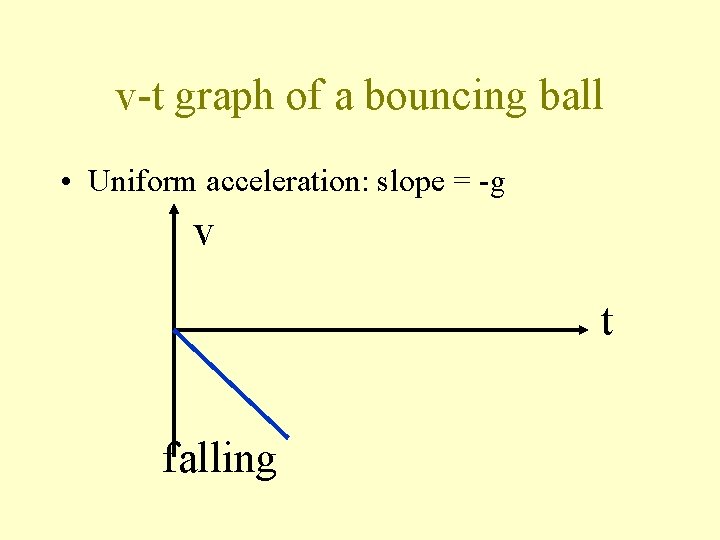
v-t graph of a bouncing ball • Uniform acceleration: slope = -g v t falling

Bouncing ball with energy loss Let upward vector quantities be positive. Rebound: with large acceleration a.
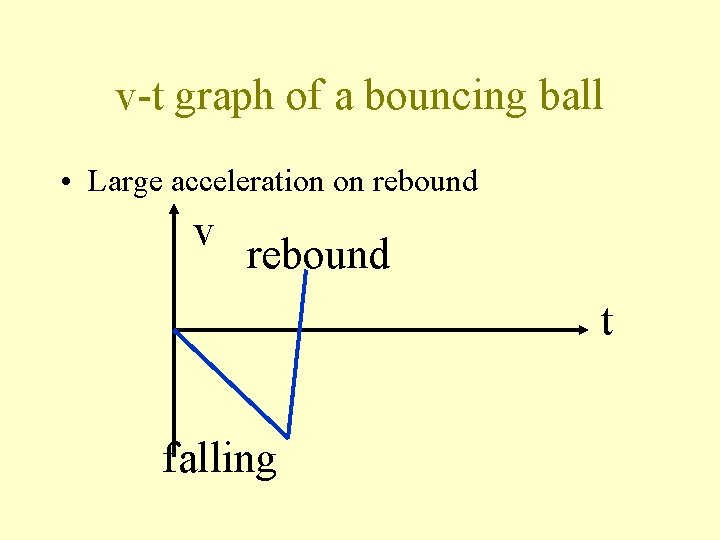
v-t graph of a bouncing ball • Large acceleration on rebound v rebound t falling

Bouncing ball with energy loss Let upward vector quantities be positive. Rising: with uniform acceleration a = -g.
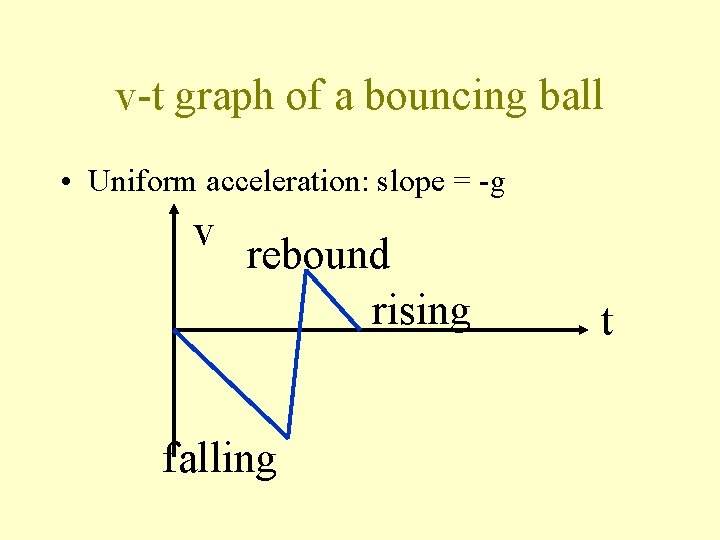
v-t graph of a bouncing ball • Uniform acceleration: slope = -g v rebound rising falling t
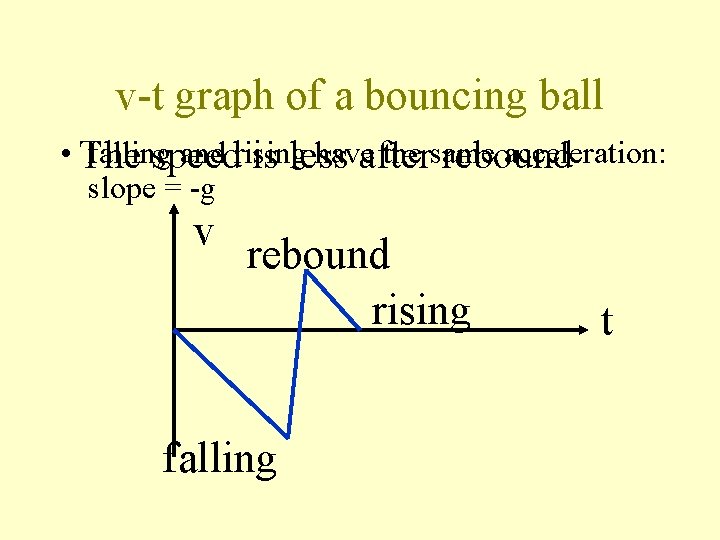
v-t graph of a bouncing ball • The falling and rising have the same acceleration: speed is less after rebound slope = -g v rebound rising falling t
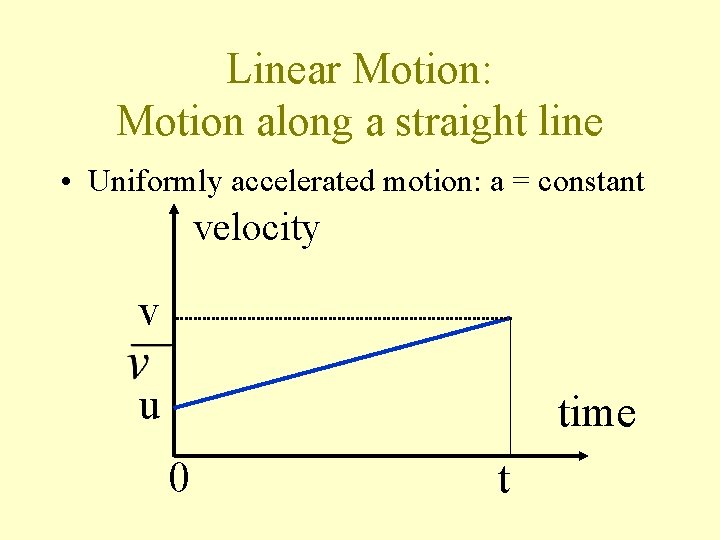
Linear Motion: Motion along a straight line • Uniformly accelerated motion: a = constant velocity v u time 0 t

Uniformly accelerated motion • u = initial velocity (velocity at time = 0). • v = final velocity (velocity at time = t). • a = acceleration v = u + at
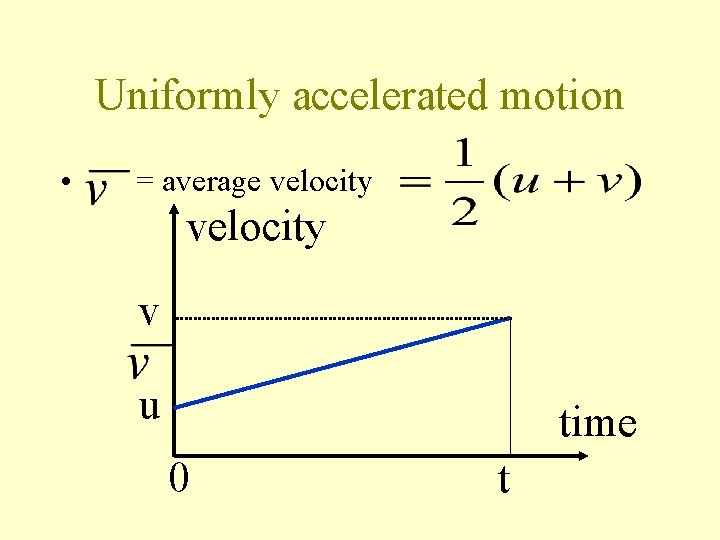
Uniformly accelerated motion • = average velocity v u time 0 t
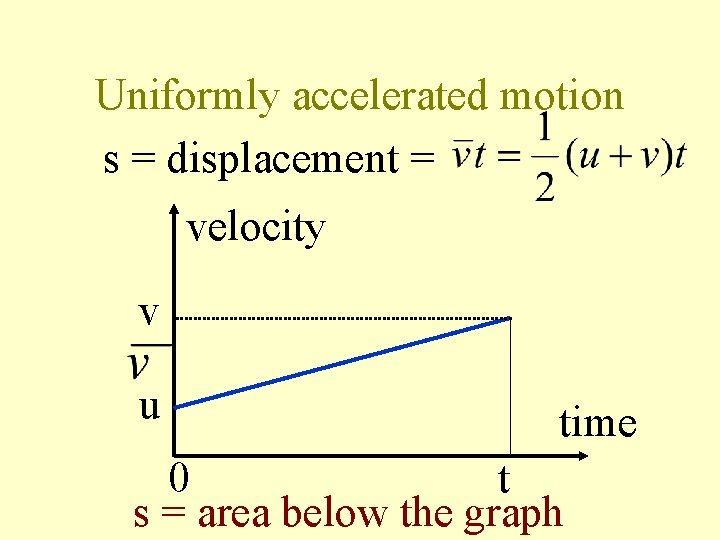
Uniformly accelerated motion s = displacement = velocity v u time 0 t s = area below the graph

Equations of uniformly accelerated motion

Uniformly accelerated motion • Example 17

Free falling: uniformly accelerated motion Let downward vector quantities be negative a = -g

Free falling: uniformly accelerated motion a = -g

Free falling: uniformly accelerated motion Example 18

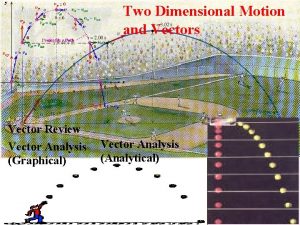
Parabolic Motion • Two dimensional motion under constant acceleration. • There is acceleration perpendicular to the initial velocity • Examples: – Projectile motion under gravity. – Electron moves into a uniform electric field.
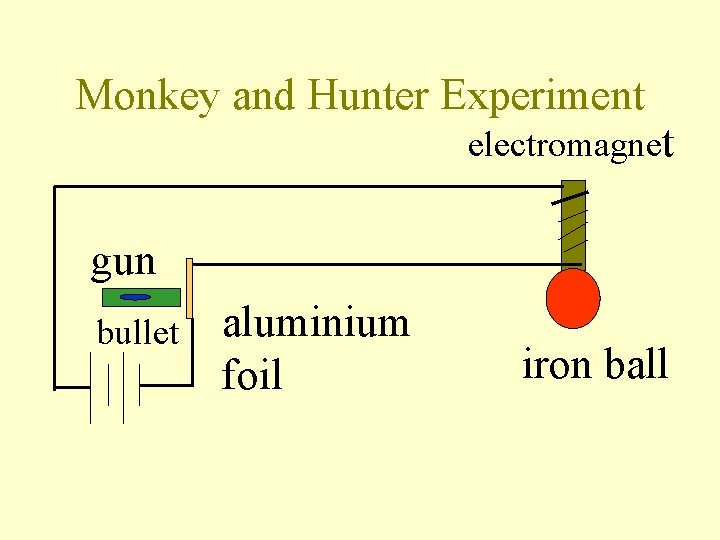
Monkey and Hunter Experiment electromagnet gun bullet aluminium foil iron ball
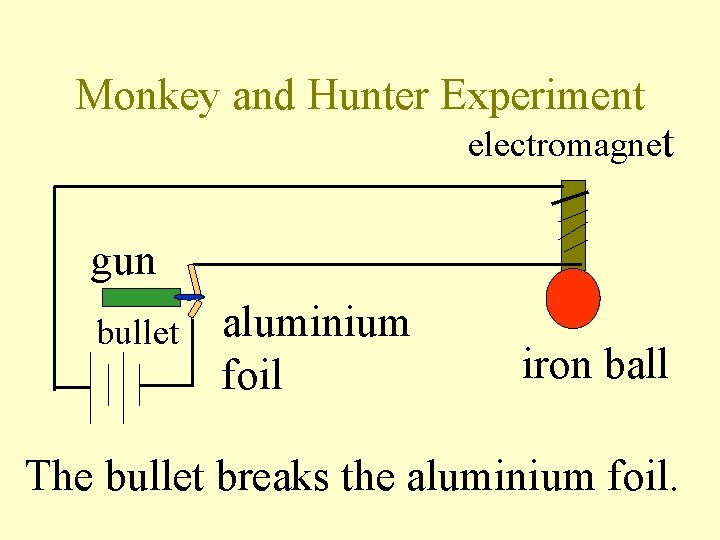
Monkey and Hunter Experiment electromagnet gun bullet aluminium foil iron ball The bullet breaks the aluminium foil.
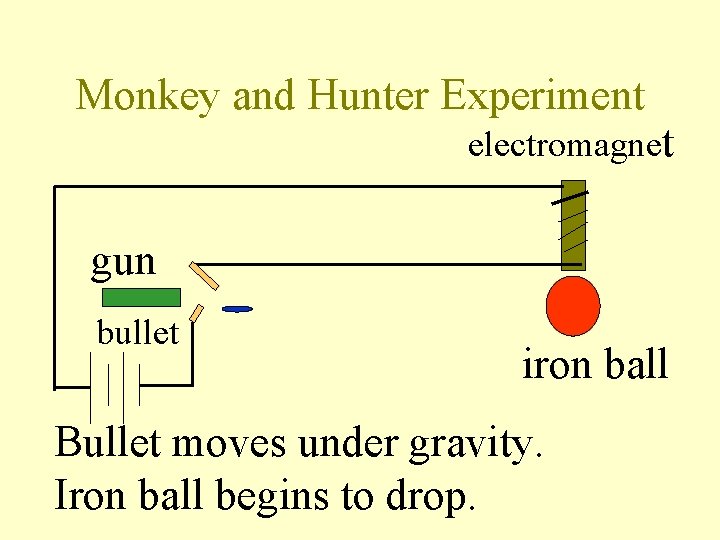
Monkey and Hunter Experiment electromagnet gun bullet iron ball Bullet moves under gravity. Iron ball begins to drop.
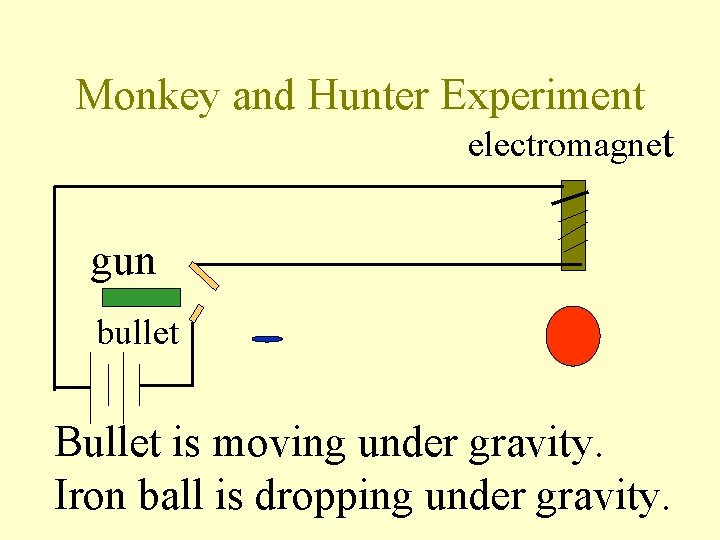
Monkey and Hunter Experiment electromagnet gun bullet Bullet is moving under gravity. Iron ball is dropping under gravity.
Monkey and Hunter Experiment electromagnet gun
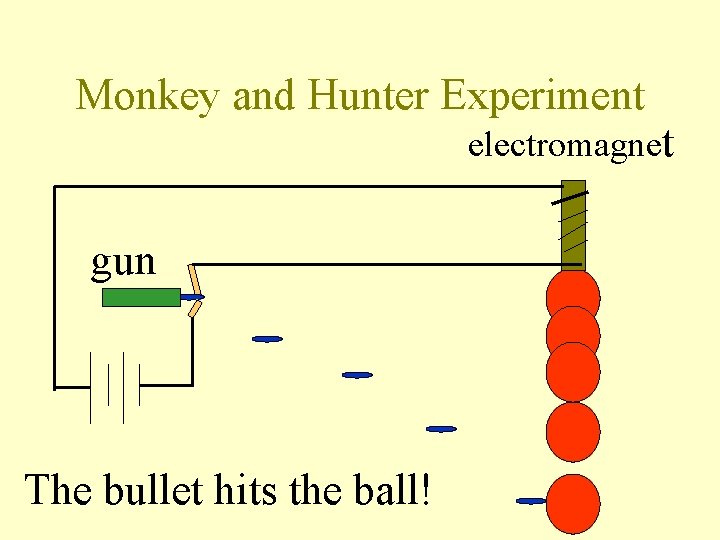
Monkey and Hunter Experiment electromagnet gun The bullet hits the ball!

Monkey and Hunter Experiment • The vertical motions of both the bullet and the iron are the same. • The vertical motion of the bullet is independent of its horizontal motion.
y Projectile trajectory x
y Projectile trajectory x
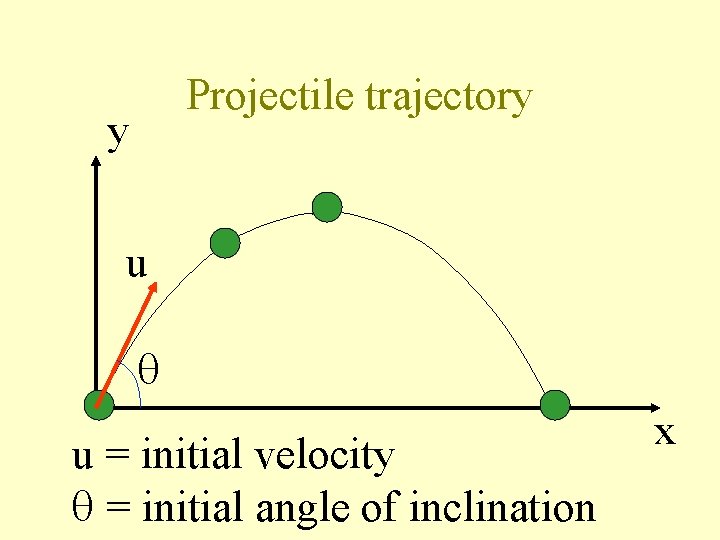
Projectile trajectory y u u = initial velocity = initial angle of inclination x
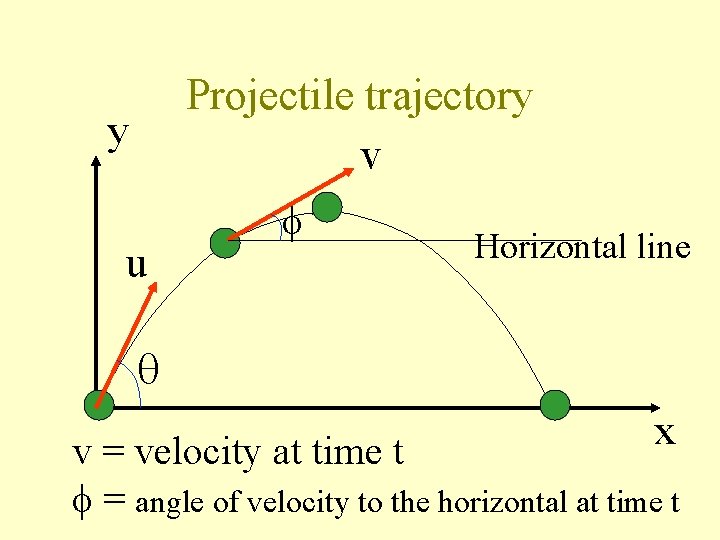
Projectile trajectory v y u Horizontal line x v = velocity at time t = angle of velocity to the horizontal at time t
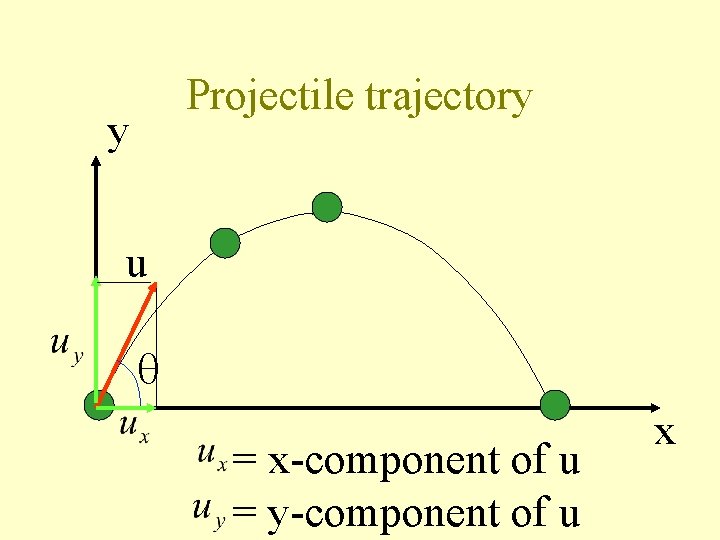
Projectile trajectory y u = x-component of u = y-component of u x
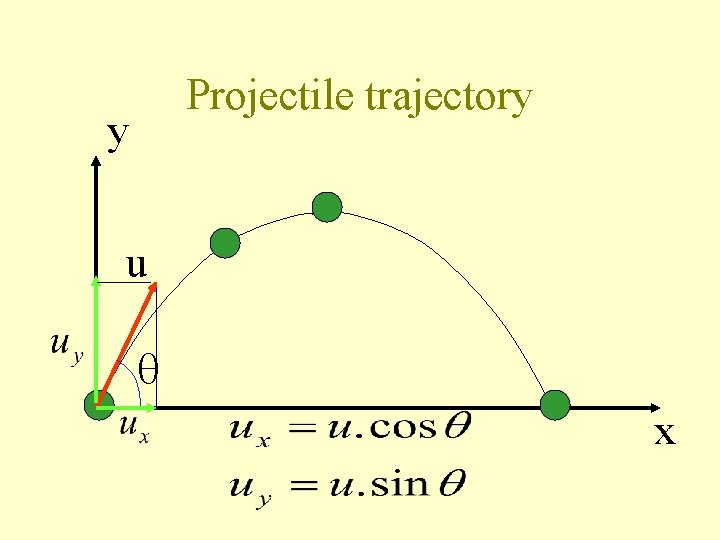
Projectile trajectory y u x
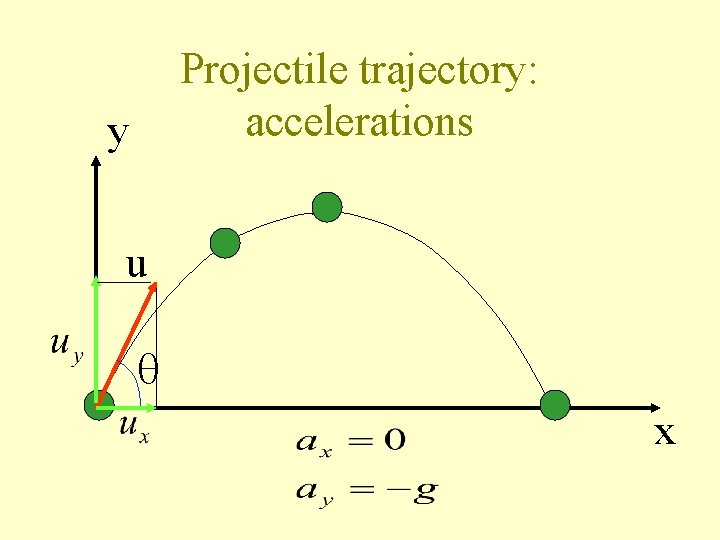
Projectile trajectory: accelerations y u x
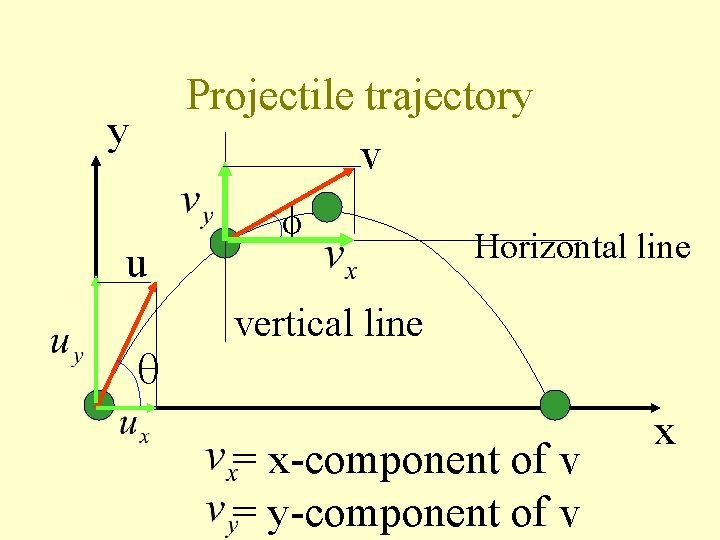
Projectile trajectory v y u Horizontal line vertical line = x-component of v = y-component of v x
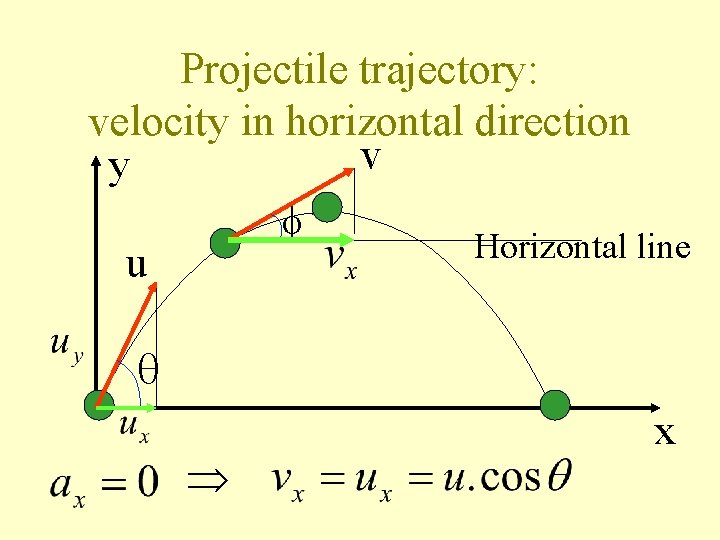
Projectile trajectory: velocity in horizontal direction v y u Horizontal line x
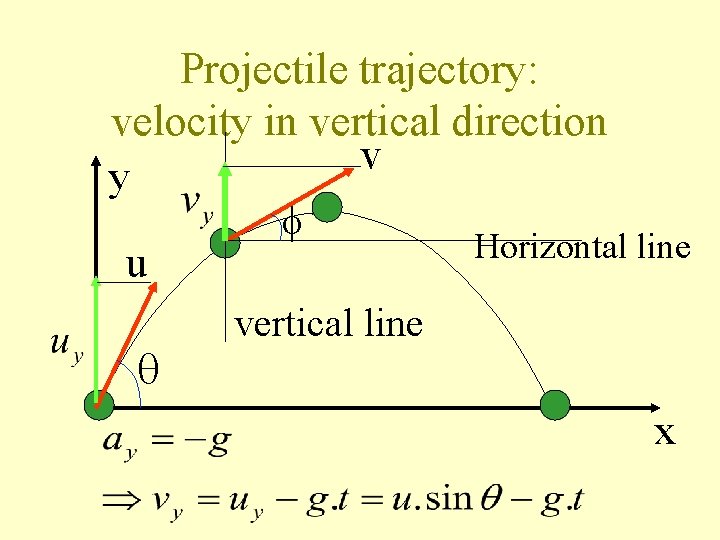
Projectile trajectory: velocity in vertical direction v y u Horizontal line vertical line x
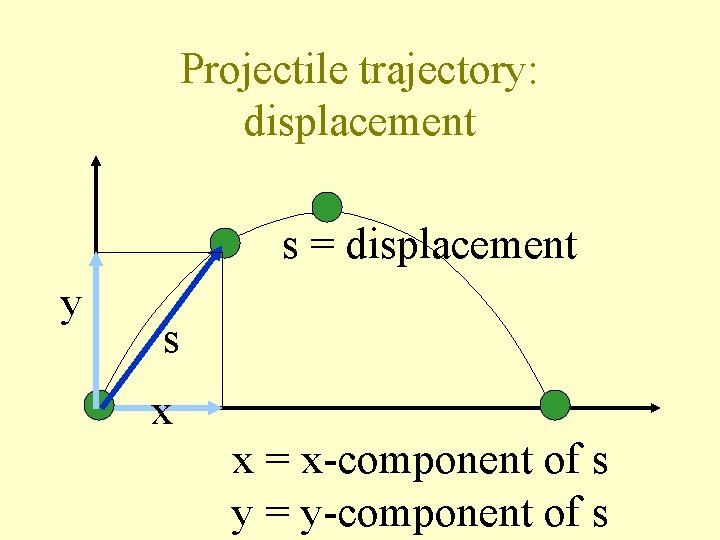
Projectile trajectory: displacement s = displacement y s x x = x-component of s y = y-component of s
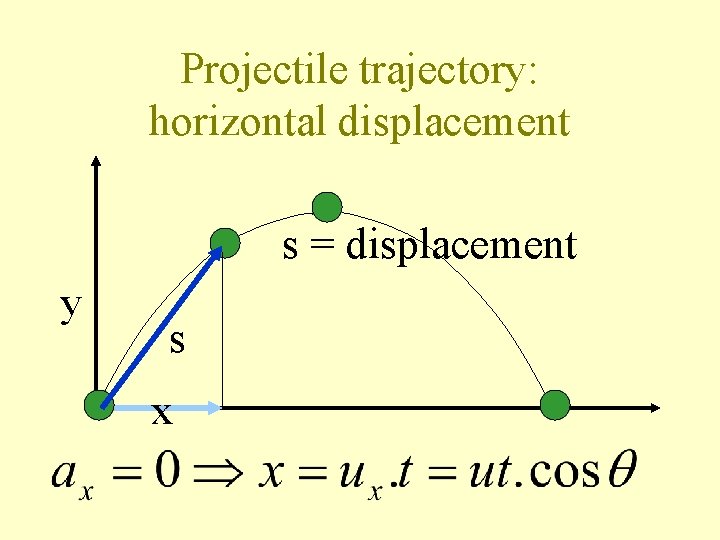
Projectile trajectory: horizontal displacement s = displacement y s x
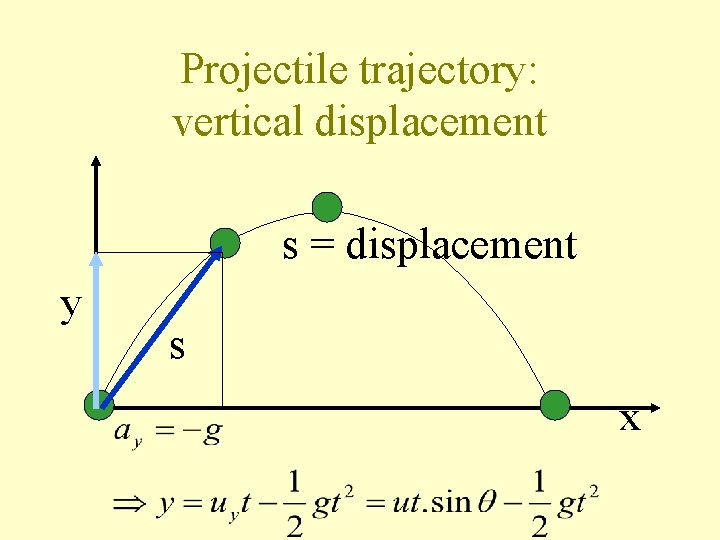
Projectile trajectory: vertical displacement s = displacement y s x
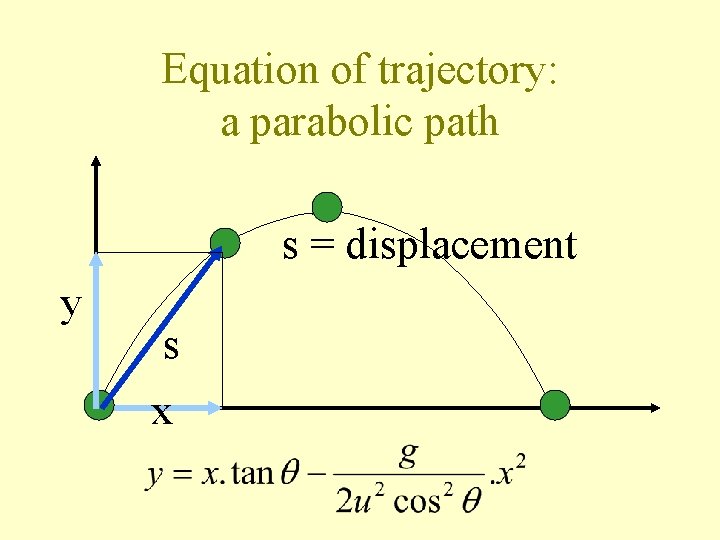
Equation of trajectory: a parabolic path s = displacement y s x
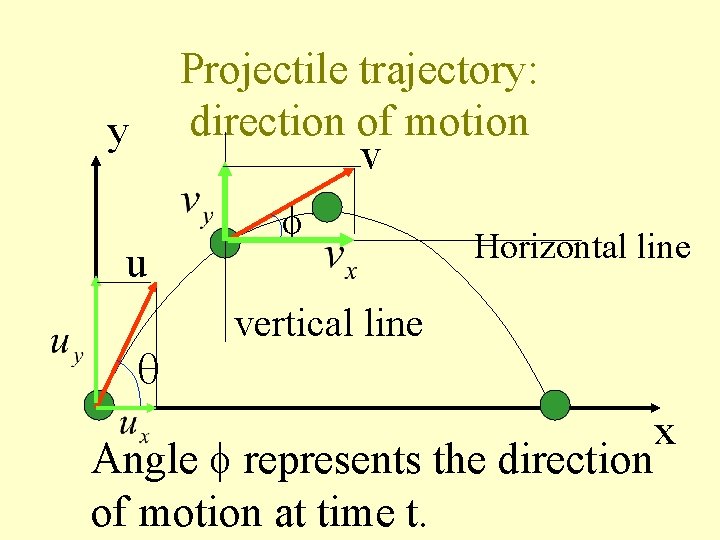
Projectile trajectory: direction of motion v y u Horizontal line vertical line Angle represents the direction of motion at time t. x
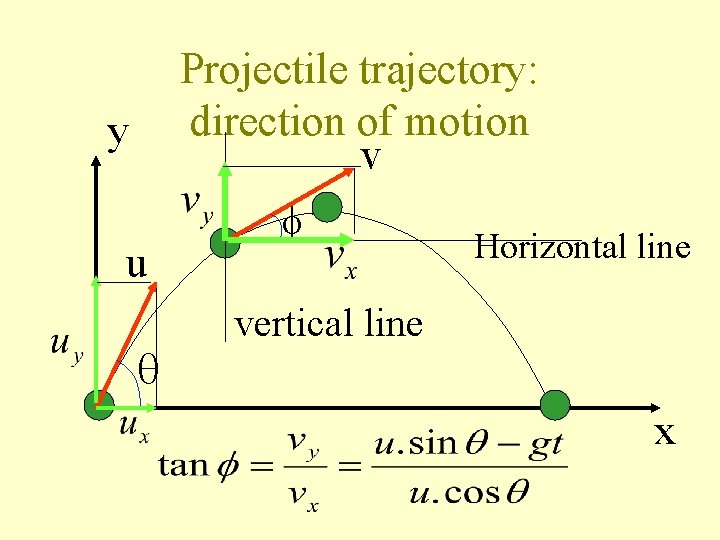
Projectile trajectory: direction of motion v y u Horizontal line vertical line x

Projectile trajectory • Example 19
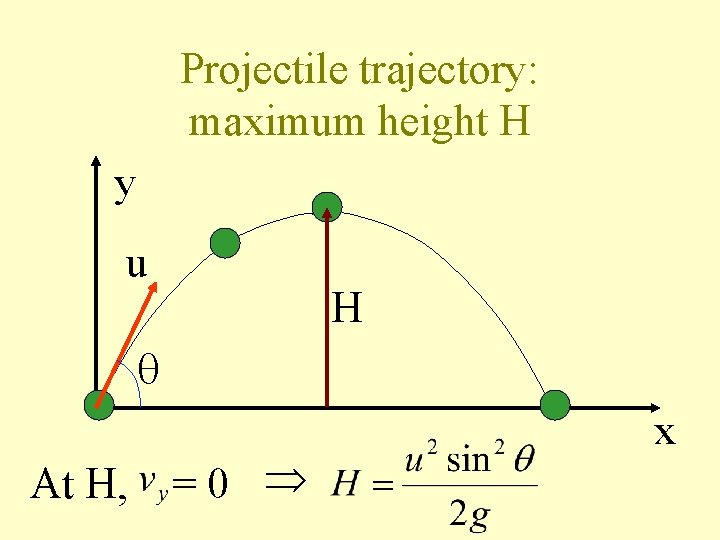
Projectile trajectory: maximum height H y u H At H, =0 x
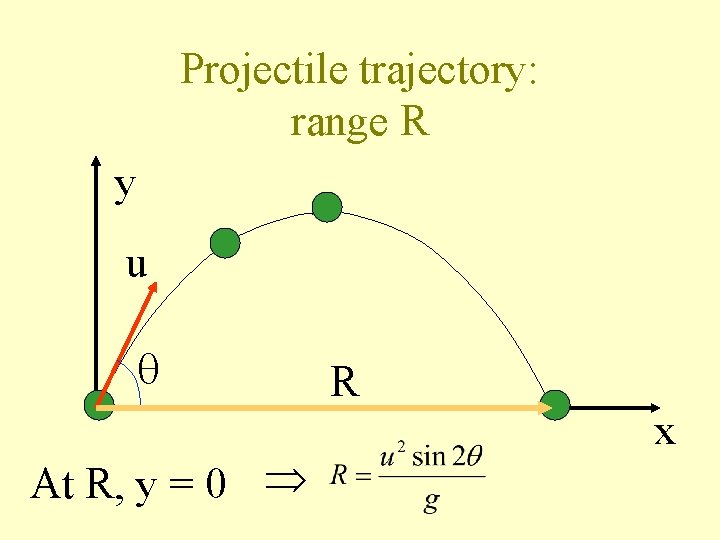
Projectile trajectory: range R y u At R, y = 0 R x
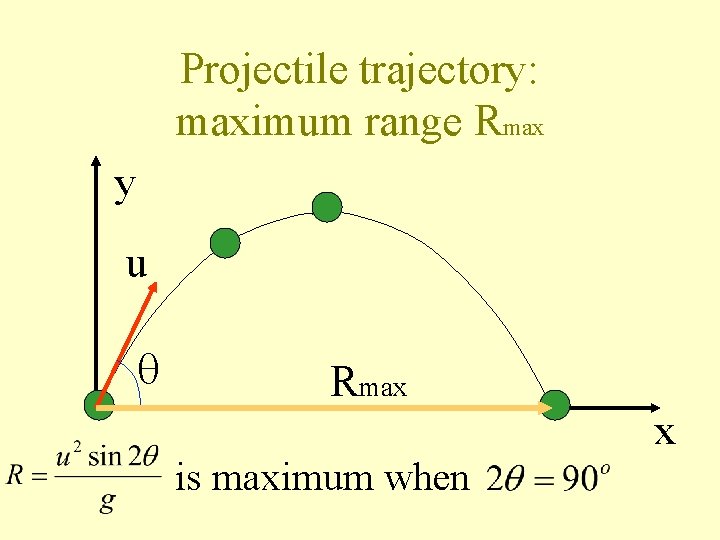
Projectile trajectory: maximum range Rmax y u Rmax is maximum when x
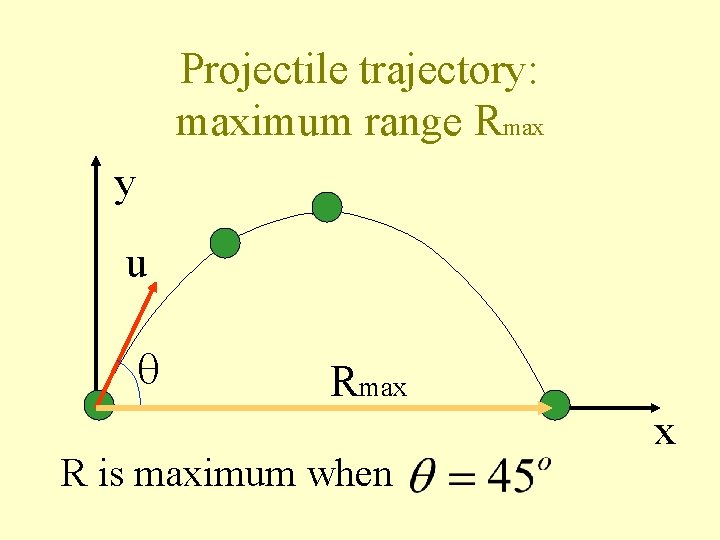
Projectile trajectory: maximum range Rmax y u Rmax R is maximum when x
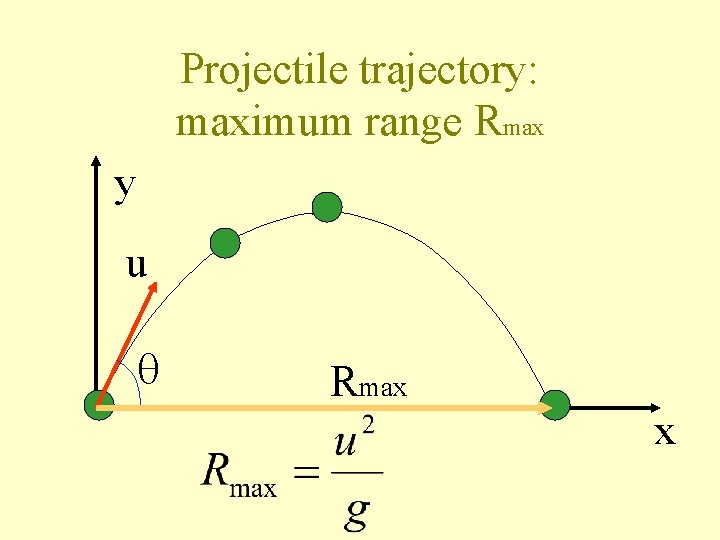
Projectile trajectory: maximum range Rmax y u Rmax x
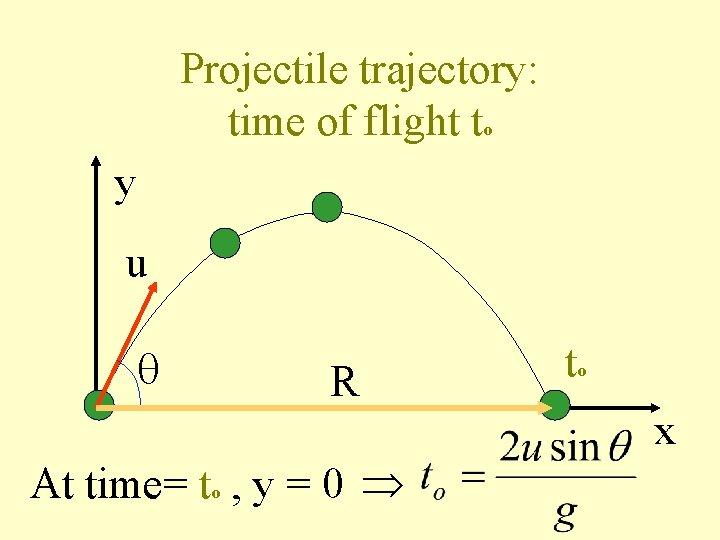
Projectile trajectory: time of flight to y u R At time= to , y = 0 to x
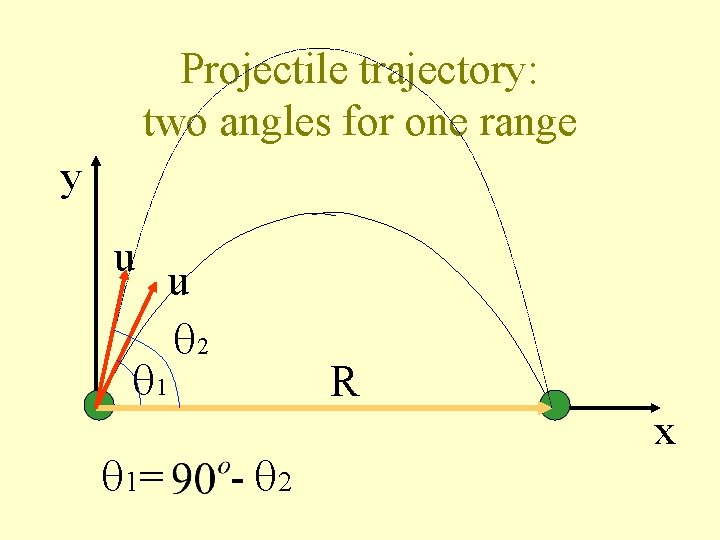
Projectile trajectory: two angles for one range y u u 2 1 1= R - 2 x
- Slides: 84