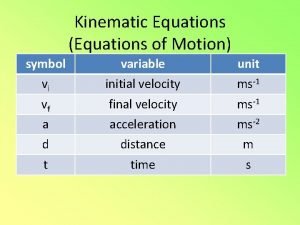
Chapter 12 Kinematics Of A Particle 1 Chapter

Chapter 12 : Kinematics Of A Particle 1

Chapter Outline • Introduction • Rectilinear Kinematics: Continuous Motion • Rectilinear Kinematics: Erratic Motion • Curvilinear Motion: Rectangular Components • Motion of a Projectile 2

Introduction • Mechanics – the state of rest of motion of bodies subjected to the action of forces • Static – equilibrium of a body that is either at rest or moves with constant velocity • Dynamics – deals with accelerated motion of a body 1) Kinematics – treats with geometric aspects of the motion 2) Kinetics – analysis of the forces causing the motion 3

Introduction Kinematic of a Particle • The difference between a body and a particle. A body consists of many particles. A body could be treated as a particle, as long as its motion is characterized by the motion of its centre of mass and any rotation of the body is neglected. Chapter 12 to 15 is about analysis of motion of a particle. 4 © 2007 Pearson Education South Asia Pte Ltd

RECTILINEAR KINEMATICS: CONTINIOUS MOTION (Section 12. 2) A particle travels along a straight-line path defined by the coordinate axis s. The position of the particle at any instant, relative to the origin, O, is defined by the position vector r, or the scalar s. Scalar s can be positive or negative. Typical units for r and s are meters (m) or feet (ft). The displacement of the particle is defined as its change in position. Vector form: r = r’ - r Scalar form: s = s’ - s The total distance traveled by the particle, s. T, is a positive scalar that represents the total length of the path over which the particle travels. © 2007 Pearson Education South Asia Pte Ltd

Rectilinear Kinematics: Continuous Motion Velocity Average velocity, Instantaneous velocity is defined as 6

Rectilinear Kinematics: Continuous Motion Representing as an algebraic scalar, Velocity is +ve = particle moving to the right Velocity is –ve = Particle moving to the left Magnitude of velocity is the speed (m/s) 7

Rectilinear Kinematics: Continuous Motion Average speed is defined as total distance traveled by a particle, s. T, divided by the elapsed time. The particle travels along the path of length s. T in time => 8

Rectilinear Kinematics: Continuous Motion Acceleration velocity of particle is known at points P and P’ during time interval Δt, average acceleration is Δv represents difference in the velocity during the time interval Δt, ie 9

Rectilinear Kinematics: Continuous Motion Instantaneous acceleration at time t is found by taking smaller and smaller values of Δt and corresponding smaller and smaller values of Δv, 10

Rectilinear Kinematics: Continuous Motion - Constant Acceleration In previous slide, acceleration is defined as, acceleration is in the function of time. However, we may encounter a case where acceleration is constant (equal to a number rather in a funtion of time). See next slides. 11 © 2007 Pearson Education South Asia Pte Ltd

Rectilinear Kinematics: Continuous Motion - Constant Acceleration • Velocity as a Function of Time • ac is constant equal to any number, Integrate ac = dv/dt, assuming that initially v = v 0 when t = 0. ac : constant acceleration 12

Rectilinear Kinematics: Continuous Motion - Constant Acceleration • Position as a Function of Time Integrate v = ds/dt = v 0 + act, assuming that initially s = s 0 when t = 0 Constant Acceleration 13

Rectilinear Kinematics: Continuous Motion - Constant Acceleration • Velocity as a Function of Position Integrate v dv = ac ds, assuming that initially v = v 0 at s = s 0 Constant Acceleration 14

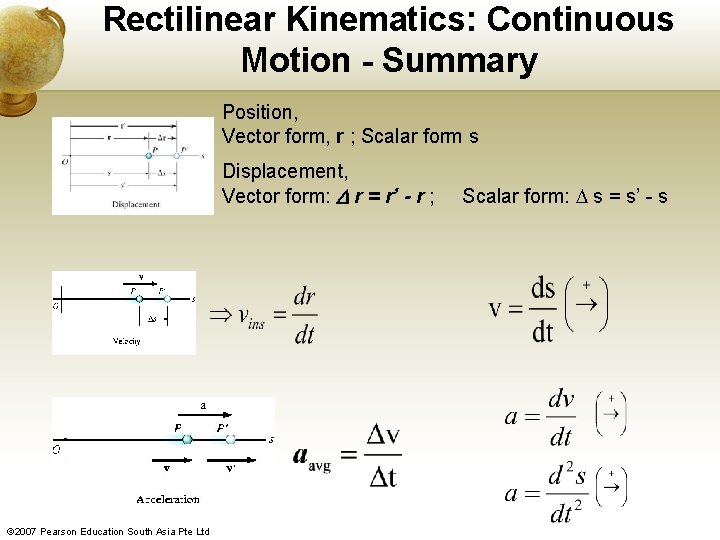
Rectilinear Kinematics: Continuous Motion - Summary Position, Vector form, r ; Scalar form s Displacement, Vector form: r = r’ - r ; © 2007 Pearson Education South Asia Pte Ltd Scalar form: s = s’ - s

Rectilinear Kinematics: Continuous Motion - Summary When acceleration is CONSTANT, where, a = ac (acceleration is a number not as a function of t). Velocity as a Function of Time - (1) Position as a Function of Time - (2) © 2007 Pearson Education South Asia Pte Ltd Velocity as a Function of Position - (3) (Eliminate t from (1) and (2))

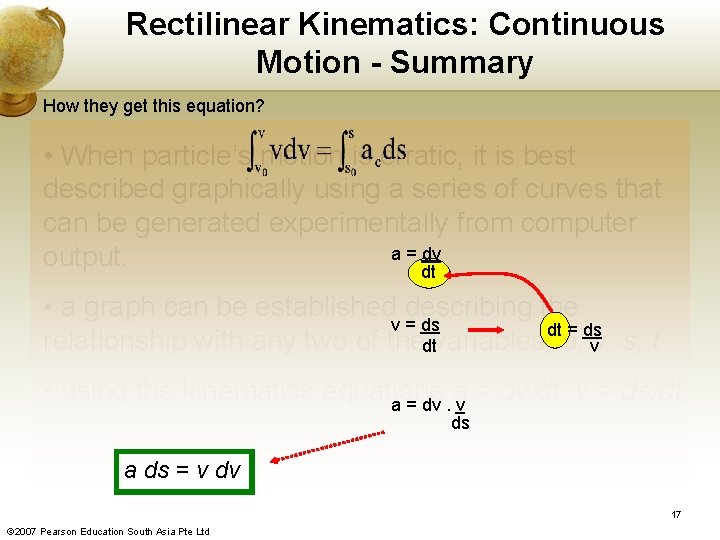
Rectilinear Kinematics: Continuous Motion - Summary How they get this equation? • When particle’s motion is erratic, it is best described graphically using a series of curves that can be generated experimentally from computer a = dv output. dt • a graph can be established describing the v = ds dt = ds relationship with any two of thedtvariables, a, vv, s, t • using the kinematics equations a = dv/dt, v = ds/dt, a = dv. v ds a ds = v dv 17 © 2007 Pearson Education South Asia Pte Ltd

EXAMPLE 1 - Rectilinear, Continuous The car moves in a straight line such that for a short time its velocity is defined by v = (0. 9 t 2 + 0. 6 t) m/s where t is in sec. Determine it position and acceleration when t = 3 s. When t = 0, s = 0. 18

EXAMPLE 1 - Rectilinear, Continuous Solution: Coordinate System. The position coordinate extends from the fixed origin O to the car, positive to the right. Position. Since v = f(t), the car’s position can be determined from v = ds/dt, since this equation relates v, s and t. Noting that s = 0 when t = 0, we have 19

EXAMPLE 1 - Rectilinear, Continuous When t = 3 s, s = 10. 8 m 20

EXAMPLE 1 -Rectilinear, Continuous Acceleration Knowing v = f(t), the acceleration is determined from a = dv/dt, since this equation relates a, v and t. When t = 3 s, a = 6 m/s 2 21

Rectilinear Kinematics: Erratic Motion Previous slides is about - Rectilinear Kinematics, Continuous Motion. This slide is about - Rectilinear Kinematics, Erratic Motion. What is the difference between Continuous and Erratic motion? Erratic motion Continuous motion Velocity could be represented using a single continuous mathematical equation 22

Rectilinear Kinematics: Erratic Motion • When particle’s motion is erratic, it is best described graphically using a series of curves that can be generated experimentally from computer output. • a graph can be established describing the relationship with any two of the variables, a, v, s, t • using the kinematics equations a = dv/dt, v = ds/dt, a ds = v dv 23 © 2007 Pearson Education South Asia Pte Ltd

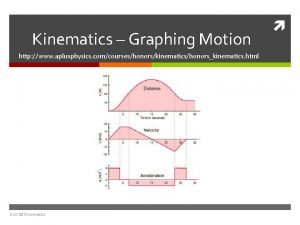
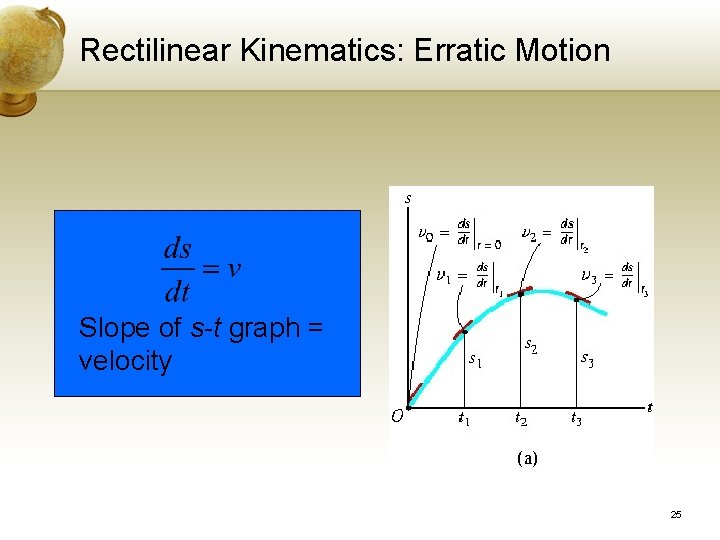
Rectilinear Kinematics: Erratic Motion Given the s-t Graph, construct the v-t Graph • The s-t graph can be plotted if the position of the particle can be determined experimentally during a period of time t. • To determine the particle’s velocity as a function of time, the v-t Graph, use v = ds/dt • Velocity as any instant is determined by measuring the slope of the s-t graph 24

Rectilinear Kinematics: Erratic Motion Slope of s-t graph = velocity 25

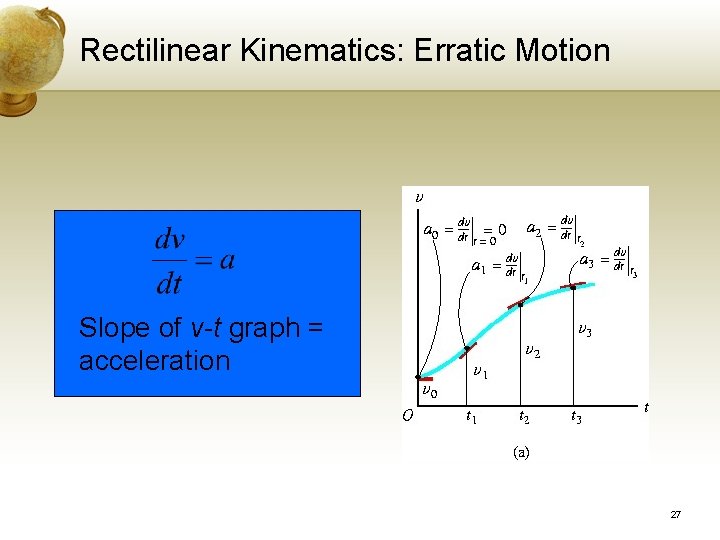
Rectilinear Kinematics: Erratic Motion Given the v-t Graph, construct the a-t Graph • When the particle’s v-t graph is known, the acceleration as a function of time, the a-t graph can be determined using a = dv/dt • Acceleration as any instant is determined by measuring the slope of the v-t graph 26

Rectilinear Kinematics: Erratic Motion Slope of v-t graph = acceleration 27

Rectilinear Kinematics: Erratic Motion • Since differentiation reduces a polynomial of degree n to that of degree n-1, then if the s-t graph is parabolic (2 nd degree curve), the v-t graph will be sloping line (1 st degree curve), and the a-t graph will be a constant or horizontal line (zero degree curve) 28

EXAMPLE 2 - Rectilinear, Erratic A bicycle moves along a straight road such that it position is described by the graph as shown. Construct the v-t and a-t graphs for 0 ≤ t ≤ 30 s. 29

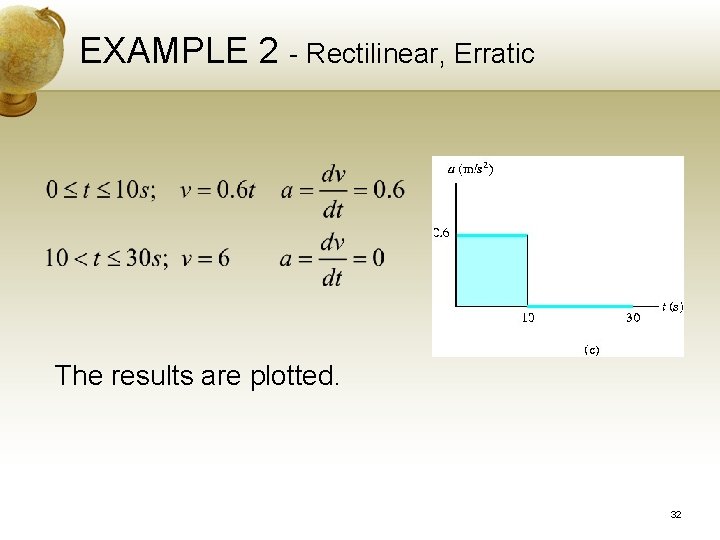
EXAMPLE 2 - Rectilinear, Erratic Solution: v-t Graph. The v-t graph can be determined by differentiating the eqns defining the s-t graph The results are plotted. 30

EXAMPLE 2 - Rectilinear, Erratic We obtain specify values of v by measuring the slope of the s-t graph at a given time instant. a-t Graph. The a-t graph can be determined by differentiating the eqns defining the lines of the v-t graph. 31

EXAMPLE 2 - Rectilinear, Erratic The results are plotted. 32

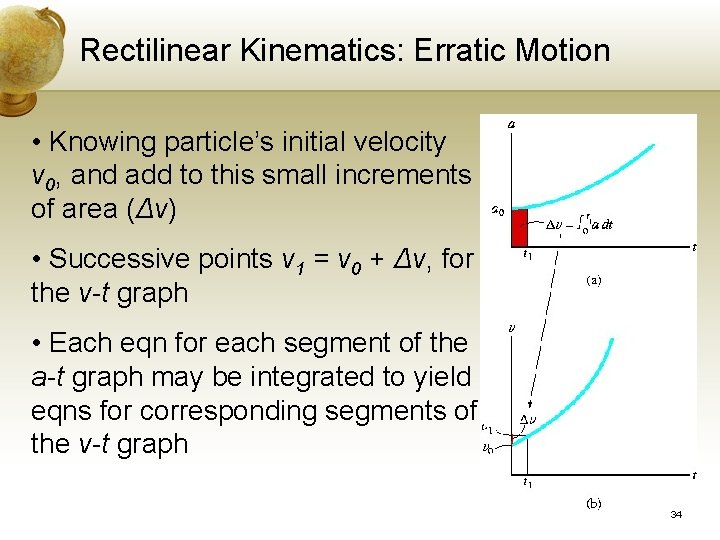
Rectilinear Kinematics: Erratic Motion Given the a-t Graph, construct the v-t Graph • When the a-t graph is known, the v-t graph may be constructed using a = dv/dt Change in = Area under velocity a-t graph 33

Rectilinear Kinematics: Erratic Motion • Knowing particle’s initial velocity v 0, and add to this small increments of area (Δv) • Successive points v 1 = v 0 + Δv, for the v-t graph • Each eqn for each segment of the a-t graph may be integrated to yield eqns for corresponding segments of the v-t graph 34

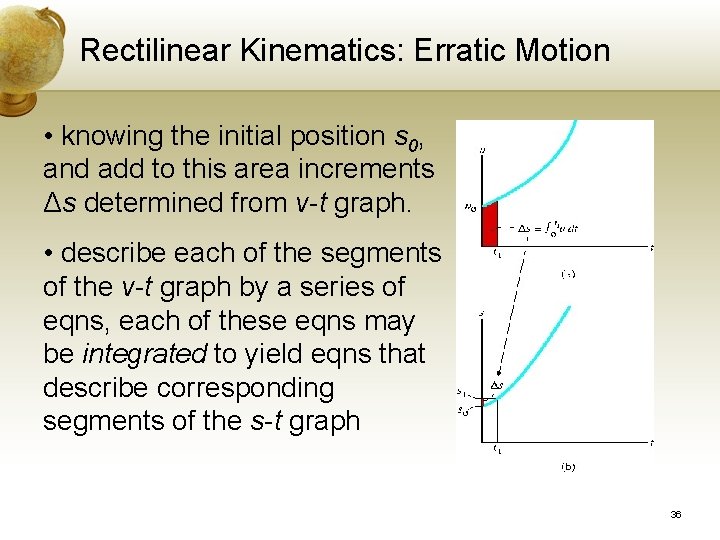
Rectilinear Kinematics: Erratic Motion Given the v-t Graph, construct the s-t Graph • When the v-t graph is known, the s-t graph may be constructed using v = ds/dt Displacement = Area under v -t graph 35

Rectilinear Kinematics: Erratic Motion • knowing the initial position s 0, and add to this area increments Δs determined from v-t graph. • describe each of the segments of the v-t graph by a series of eqns, each of these eqns may be integrated to yield eqns that describe corresponding segments of the s-t graph 36

EXAMPLE 3 - Rectilinear, Erratic A test car starts from rest and travels along a straight track such that it accelerates at a constant rate for 10 s and then decelerates at a constant rate. Draw the v-t and s-t graphs and determine the time t’ needed to stop the car. How far has the car traveled? How could at initial velocity = 0 m/s, acceleration is not 0. 37

EXAMPLE 3 Solution: v-t Graph. The v-t graph can be determined by integrating the straight-line segments of the a-t graph. Using initial condition v = 0 when t = 0, 38

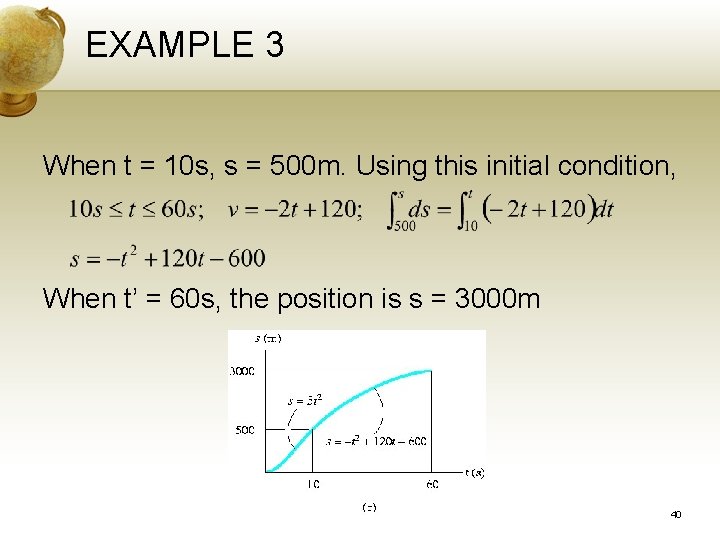
EXAMPLE 3 When t = 10 s, v = 100 m/s, using this as initial condition for the next time period, we have When t = t’ we require v = 0. This yield t’ = 60 s s-t Graph. Integrating the eqns of the v-t graph yields the corresponding eqns of the s-t graph. Using the initial conditions s = 0 when t = 0, 39

EXAMPLE 3 When t = 10 s, s = 500 m. Using this initial condition, When t’ = 60 s, the position is s = 3000 m 40

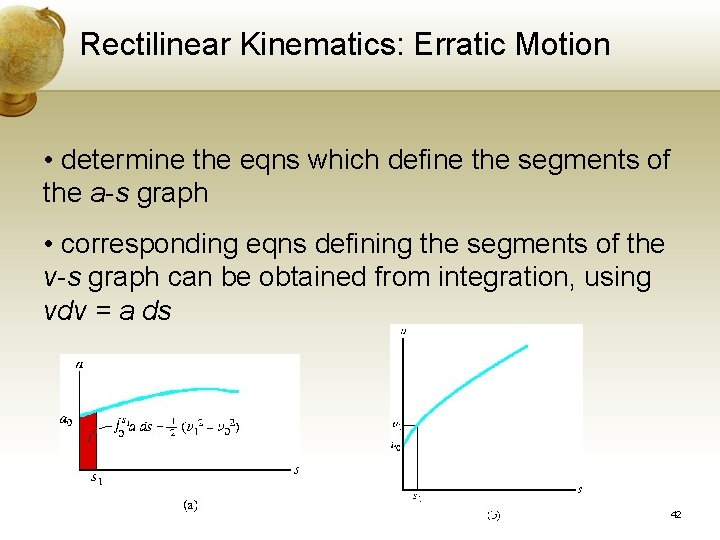
Rectilinear Kinematics: Erratic Motion Given the a-s Graph, construct the v-s Graph • v-s graph can be determined by using v dv = a ds, integrating this eqn between the limit v = v 0 at s = s 0 and v = v 1 at s = s 1 Area under a-s graph 41

Rectilinear Kinematics: Erratic Motion • determine the eqns which define the segments of the a-s graph • corresponding eqns defining the segments of the v-s graph can be obtained from integration, using vdv = a ds 42

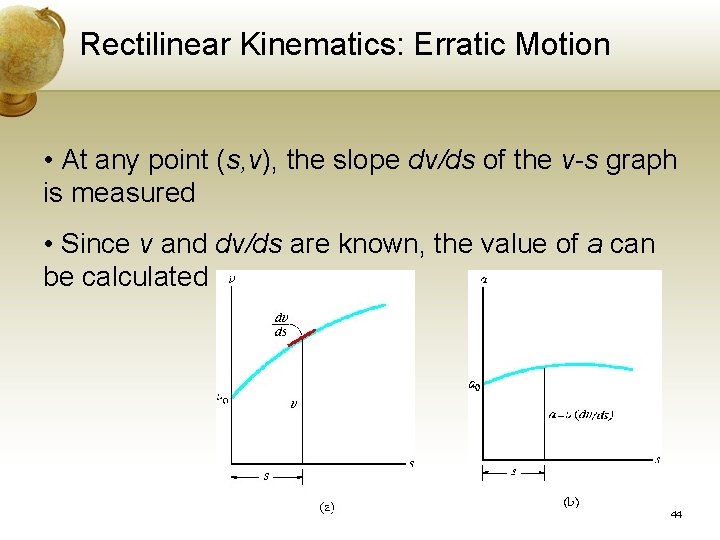
Rectilinear Kinematics: Erratic Motion Given the v-s Graph, construct the a-s Graph • v-s graph is known, the acceleration a at any position s can be determined using a ds = v dv Acceleration = velocity times slope of v-s graph 43

Rectilinear Kinematics: Erratic Motion • At any point (s, v), the slope dv/ds of the v-s graph is measured • Since v and dv/ds are known, the value of a can be calculated 44

EXAMPLE 4 - Rectilinear, Erratic The v-s graph describing the motion of a motorcycle is shown in Fig 12 -15 a. Construct the a-s graph of the motion and determine the time needed for the motorcycle to reach the position s = 120 m. 45

EXAMPLE 4 - Rectilinear, Erratic Solution: a-s Graph Since the eqns for the segments of the v-s graph are given, a-s graph can be determined using a ds = v dv. 46

EXAMPLE 4 - Rectilinear, Erratic Time The time can be obtained using v-s graph and v = ds/dt. For the first segment of motion, s = 0 at t = 0, At s = 60 m, t = 8. 05 s 47

EXAMPLE 4 - Rectilinear, Erratic For second segment of motion, At s = 120 m, t = 12. 0 s 48

General Curvilinear Motion Previously, we discussed about “rectilinear motion”, now we discuss about “curvelinear motion” - when particle moves along curved path. Curvilinear motion occurs when the particle moves along a curved path Position. The position of the particle, measured from a fixed point O, is designated by the position vector r = r(t). 49

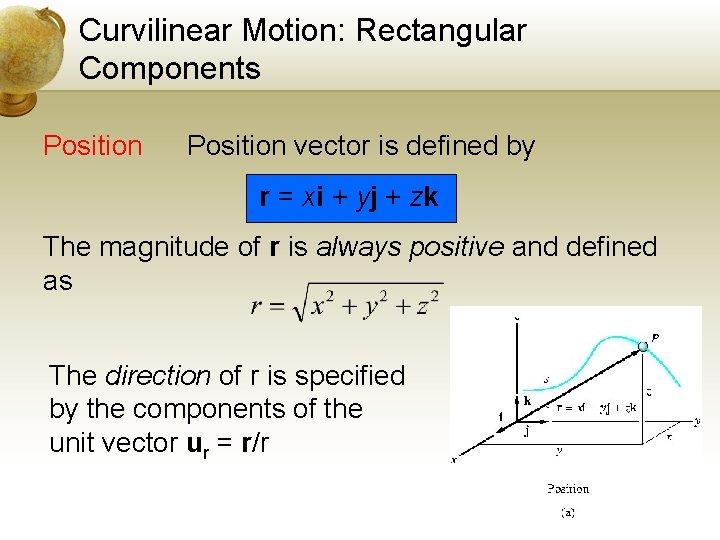
Curvilinear Motion: Rectangular Components Position vector is defined by r = xi + yj + zk The magnitude of r is always positive and defined as The direction of r is specified by the components of the unit vector ur = r/r 55

Curvilinear Motion: Rectangular Components Velocity where The velocity has a magnitude defined as the positive value of and a direction that is specified by the components of the unit vector uv=v/v and is always tangent to the path. 56

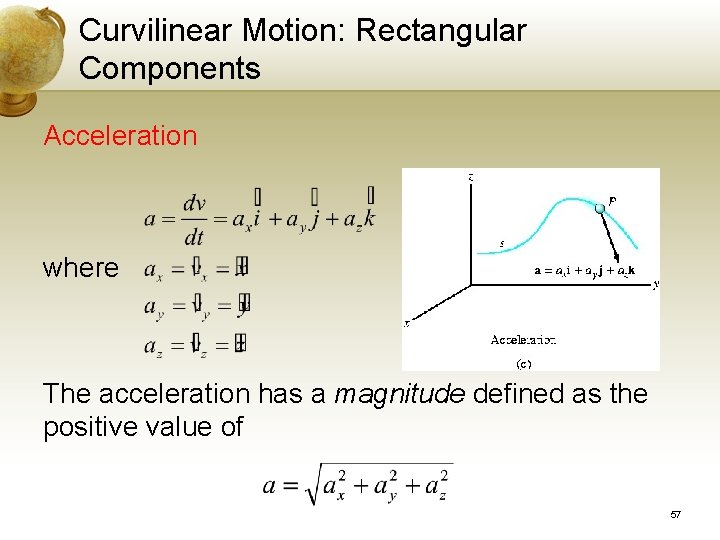
Curvilinear Motion: Rectangular Components Acceleration where The acceleration has a magnitude defined as the positive value of 57

Curvilinear Motion: Rectangular Components • The acceleration has a direction specified by the components of the unit vector ua = a/a. • Since a represents the time rate of change in velocity, a will not be tangent to the path. 58

EXAMPLE 5 - Curvelinear, Rectangular At any instant the horizontal position of the weather balloon is defined by x = (9 t) m, where t is in second. If the equation of the path is y = x 2/30, determine the distance of the balloon from the station at A, the magnitude and direction of the both the velocity and acceleration when t = 2 s. 59

EXAMPLE 5 - Curvelinear, Rectangular Solution: Position When t = 2 s, x = 9(2) m = 18 m and y = (18)2/30 = 10. 8 m The straight-line distance from A to B is m Velocity 60

EXAMPLE 5 - Curvelinear, Rectangular When t = 2 s, the magnitude of velocity is The direction is tangent to the path, where Acceleration 61

EXAMPLE 5 - Curvelinear, Rectangular The direction of a is 62

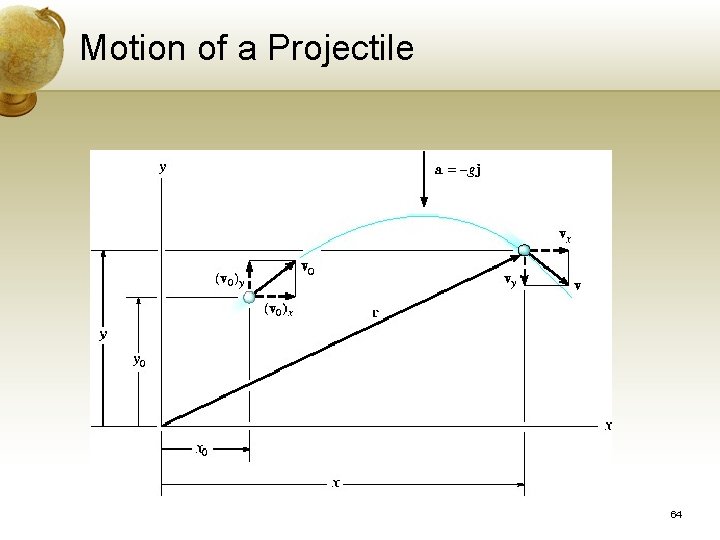
Motion of a Projectile Example of Curvelinear in Rectangular Coordinate System • Free-flight motion studied in terms of rectangular components since projectile’s acceleration always act vertically • Consider projectile launched at (x 0, y 0) • Path defined in the x-y plane • Air resistance neglected • Only force acting on the projectile is its weight, resulting in constant downwards acceleration ac = g = 9. 81 m/s 2 63

Motion of a Projectile 64

Motion of a Projectile Horizontal Motion Since ax = 0, Horizontal component of velocity remain constant during the motion 65

Motion of a Projectile Vertical ay = - g Positive y axis is directed upward, then 66

EXAMPLE 6 - Curvelinear, Rectangular, Projectile The chipping machine is designed to eject wood chips at v. O = 7. 5 m/s. If the tube is oriented at 30° from the horizontal, determine how high, h, the chips strike the pile if they land on the pile 6 m from the tube. 67

EXAMPLE 6 - Curvelinear, Rectangular, Projectile Coordinate System Three unknown h, time of flight, t. OA and the vertical component of velocity (v. B)y. Taking origin at O, for initial velocity of a chip, (v. A)x = (v. O)x = 6. 5 m/s and ay = -9. 81 m/s 2 68

EXAMPLE 6 - Curvelinear, Rectangular, Projectile Horizontal Motion Vertical Motion Relating t. OA to initial and final elevation of the chips, 69

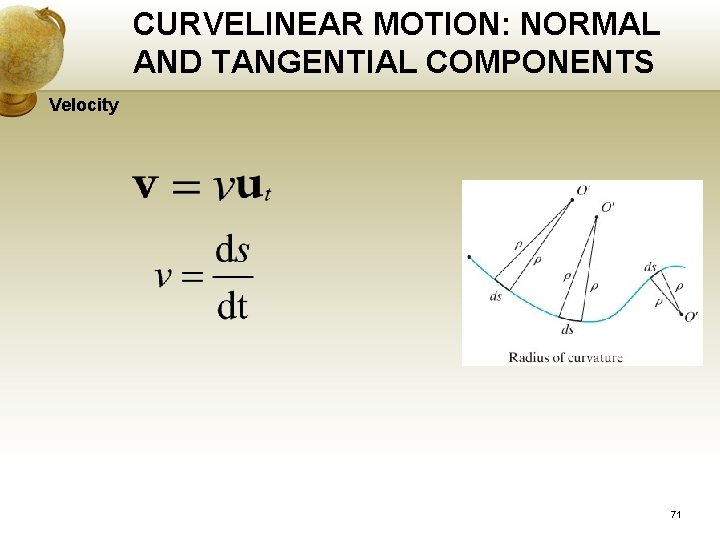
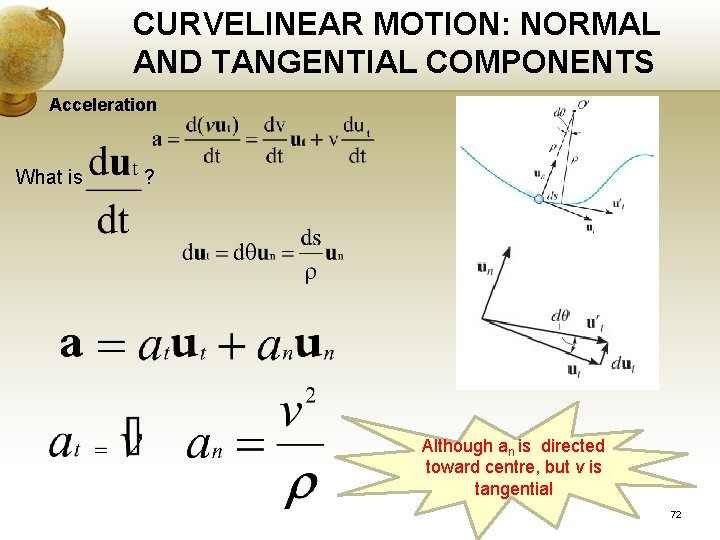
CURVELINEAR MOTION: NORMAL AND TANGENTIAL COMPONENTS Planar motion A coordinate system, its origin is on the curve, at the instant considered, the origin coincide with the location of the particle. Two axes: t axis - tangent to the curve at the point, +ve in increasing s, unit vector ut. n axis, normal to curve, pointing towards origin (always on the concave side of the curve), unit vector un. The plane contain n & t axis is called osculating plane (it is fixed in the plane of motion). 70

CURVELINEAR MOTION: NORMAL AND TANGENTIAL COMPONENTS Velocity 71

CURVELINEAR MOTION: NORMAL AND TANGENTIAL COMPONENTS Acceleration What is ? Although an is directed toward centre, but v is tangential 72

CURVELINEAR MOTION: NORMAL AND TANGENTIAL COMPONENTS Example 12. 14. 1. How to relate parabolic path function and velocity of a particle? 2. How to use acceleration equation in normal and tangential coordinate system? 3. How to determine the radius of curvature of a given path? In the case of N&T, which one is given and not given?