CHAPTER 12 KINEMATICS OF A PARTICLE KINEMATICS OF













![Rectilinear motion so=0 vo=0 s 1= 2 [m] v 1= 0. 2 s + Rectilinear motion so=0 vo=0 s 1= 2 [m] v 1= 0. 2 s +](https://slidetodoc.com/presentation_image_h2/66956152ec5b0a194ae2ac644636a50b/image-23.jpg)

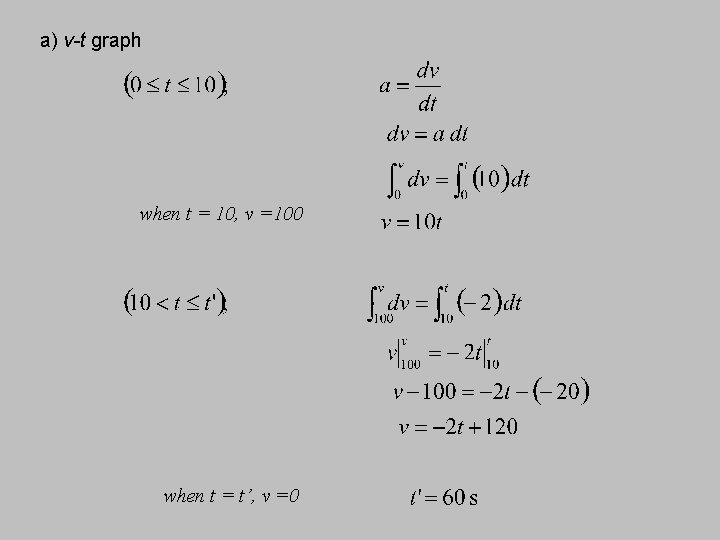
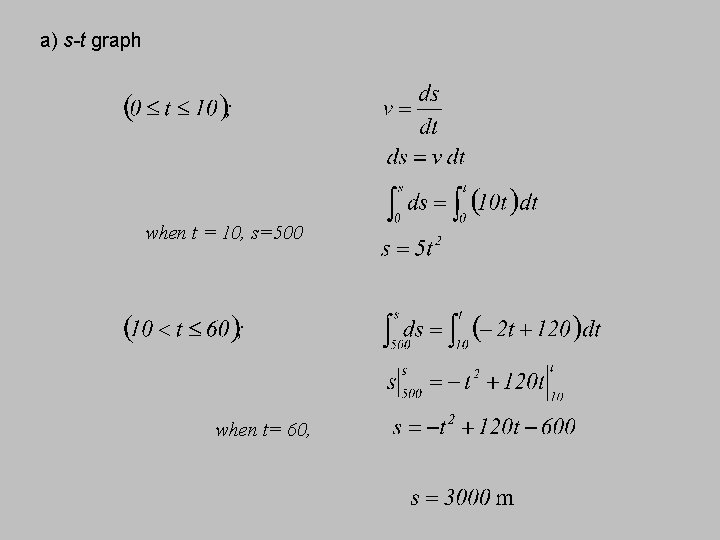
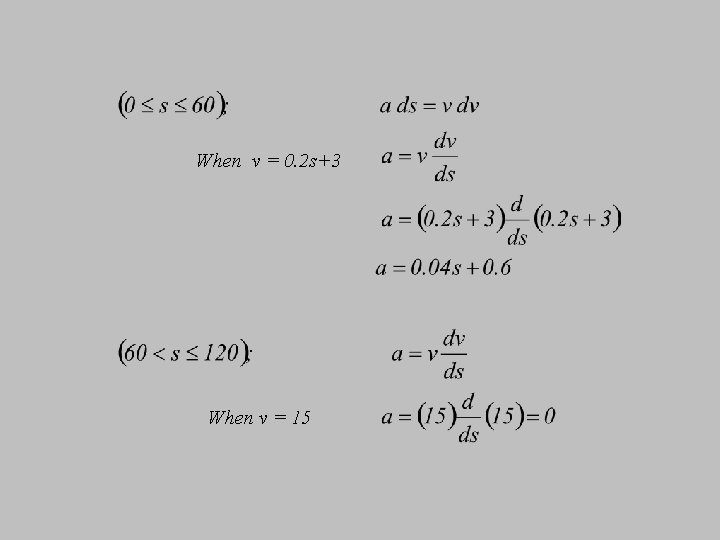
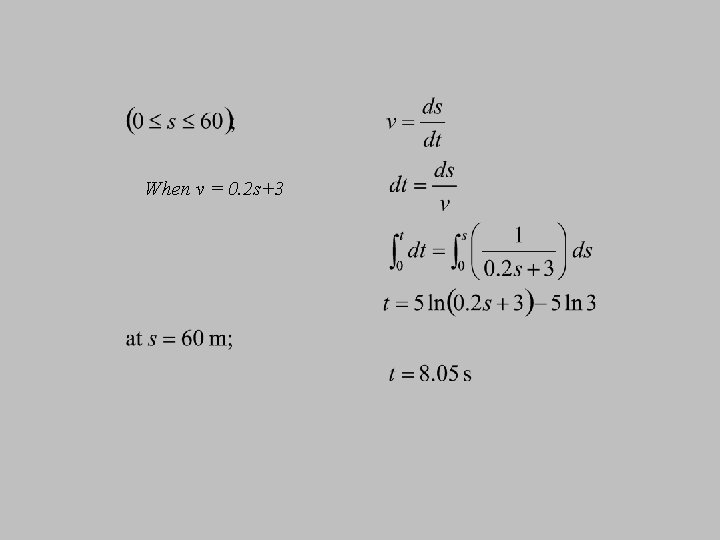
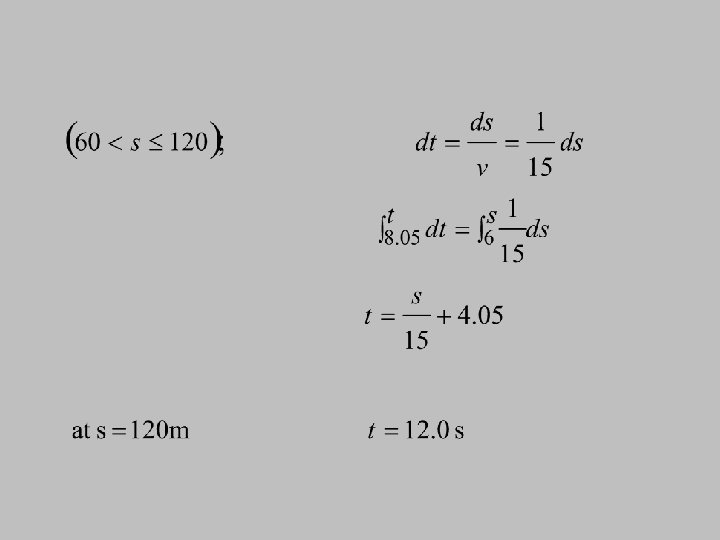



















- Slides: 71

CHAPTER 12 KINEMATICS OF A PARTICLE

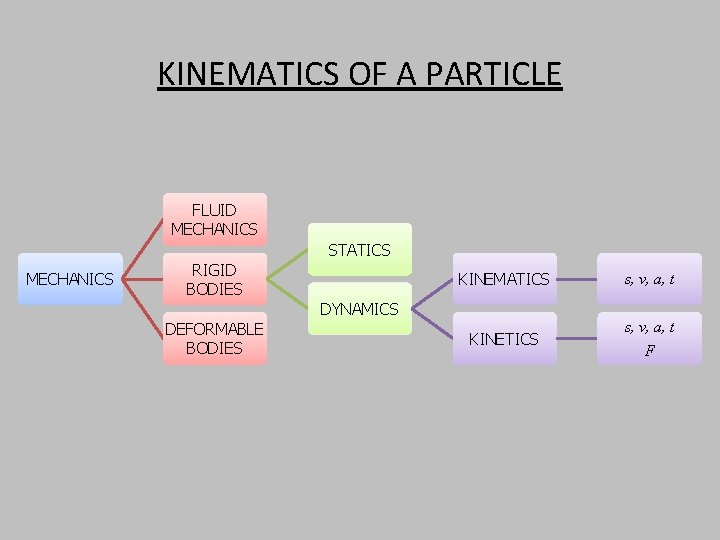
KINEMATICS OF A PARTICLE FLUID MECHANICS STATICS MECHANICS RIGID BODIES KINEMATICS s, v, a, t KINETICS s, v, a, t F DYNAMICS DEFORMABLE BODIES

OBJECTIVES 1. To introduce the concepts of position, displacement, velocity and acceleration. 2. To study particle motion along a straight line and represent this motion graphically.

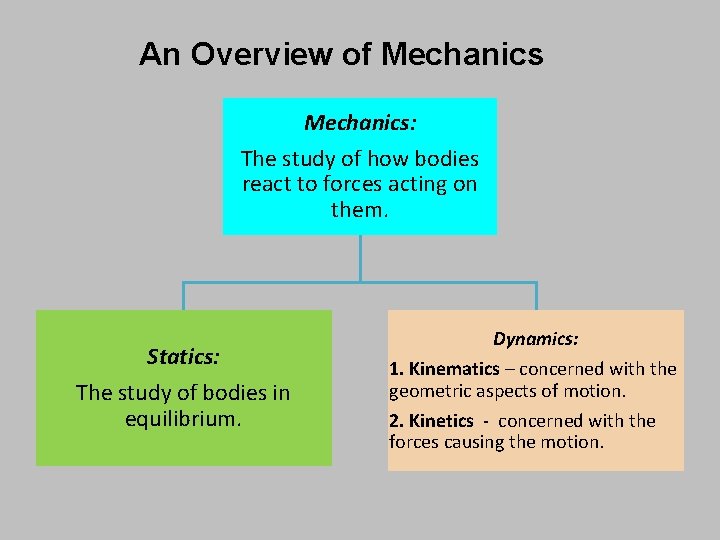
An Overview of Mechanics: The study of how bodies react to forces acting on them. Statics: The study of bodies in equilibrium. Dynamics: 1. Kinematics – concerned with the geometric aspects of motion. 2. Kinetics - concerned with the forces causing the motion.

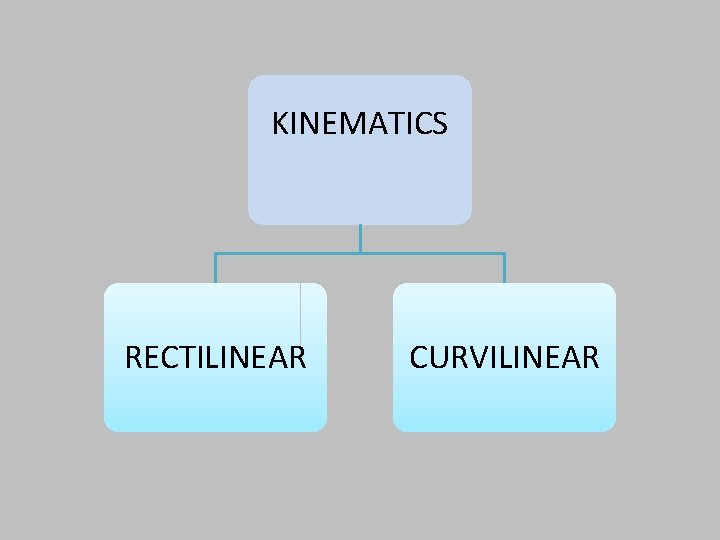
KINEMATICS RECTILINEAR CURVILINEAR

Rectilinear Kinematics – Continuous Motion Rectilinear Kinematics : The kinematics of a particle is characterized by specifying at any given instant, the particle’s position, velocity and acceleration. Displacement – s Velocity – v Accelaration – a ALL WITH THE RESPECT TO TIME - t

Displacement A particle travels along a straight-line path defined by the coordinate axis s. The position of the particle at any instant, relative to the origin, O, is defined by the position vector r, or the scalar s. Scalar s can be positive or negative. Typical units for r and s are meters (m) or feet (ft). The displacement of the particle is defined as its change in position. Vector form: r = r’ - r Scalar form: s = s’ - s The total distance traveled by the particle, s. T, is a positive scalar that represents the total length of the path over which the particle travels.

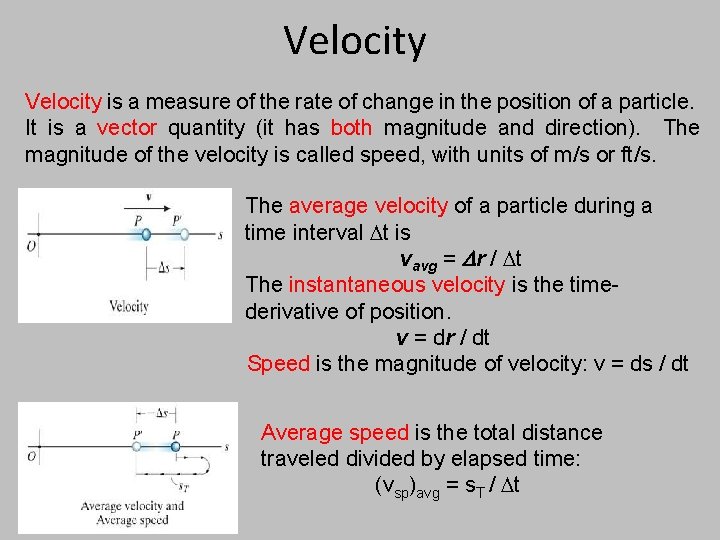
Velocity is a measure of the rate of change in the position of a particle. It is a vector quantity (it has both magnitude and direction). The magnitude of the velocity is called speed, with units of m/s or ft/s. The average velocity of a particle during a time interval t is vavg = r / t The instantaneous velocity is the timederivative of position. v = dr / dt Speed is the magnitude of velocity: v = ds / dt Average speed is the total distance traveled divided by elapsed time: (vsp)avg = s. T / t

Accelaration Acceleration is the rate of change in the velocity of a particle. It is a vector quantity. Typical units are m/s 2 or ft/s 2. The instantaneous acceleration is the time derivative of velocity. Vector form: a = dv / dt Scalar form: a = dv / dt = d 2 s / dt 2 Acceleration can be positive (speed increasing) or negative (speed decreasing). As the book indicates, the derivative equations for velocity and acceleration can be manipulated to get a ds = v dv

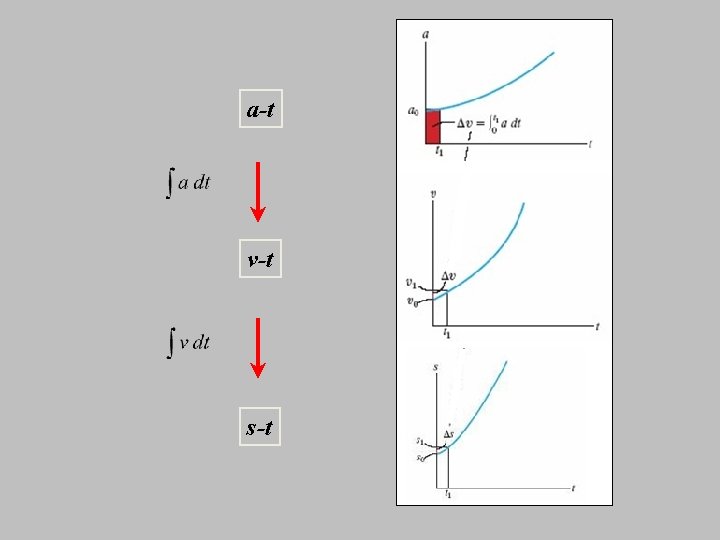
Summary Differentiate position to get velocity and acceleration. v = ds/dt ; a = dv/dt or a = v dv/ds Integrate acceleration for velocity and position. Position Velocity ò dv = ò a dt or ò v dv = ò a ds s t ò ds = ò v dt vo so o v t v s o vo so Note that so and vo represent the initial position and velocity of the particle at t = 0.

a = dv/dt Velocity as a function of time dv = a dt ò dv = ò a dt ads = vdv Velocity as a function of position v = ds/dt Position as a function of time ds= v dt ò ds = ò v dt ò v dv = ò a ds

Constant Acceleration, ac The three kinematic equations can be integrated for the special case when acceleration is constant (a = ac) to obtain very useful equations. v t ò dv = ò a dt c t = 0, s = so v = vo vo o s t so o ò ds = ò v dt v s vo so ò v dv = ò ac ds

Example 1 A motorcyclist travels along a straight road at a speed of 27 m/s. When the brakes are applied, the motorcycle decelerates at a rate of -6 t m/s 2. Find the distance the motorcycle travels before it stops. vo = 27 m/s a = - 6 t m/s 2

Solution vo = 27 m/s a = - 6 t m/s 2 1) Integrate acceleration to determine the velocity. When the motorcycle stops; v=0 0 = -3 t 2 + 27 t=3 s

hence, the distance traveled in 3 s;

Method 1 When the motorcycle stops; v=0 0 = -3 t 2 + 27 t=3 s Method 2

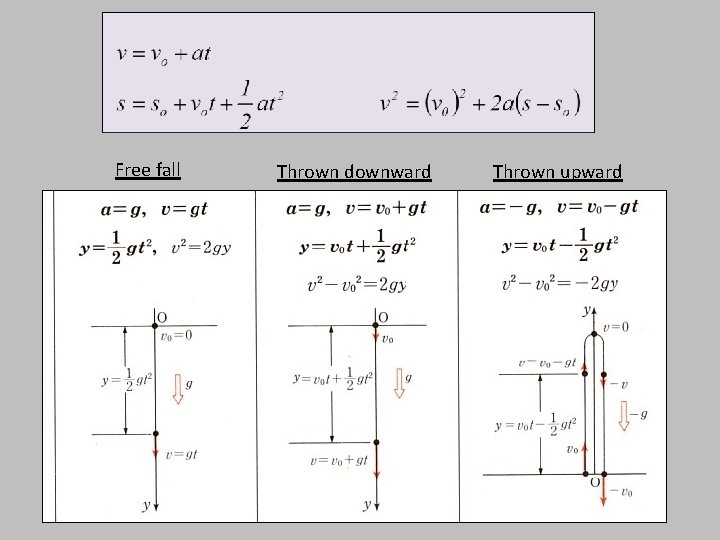
Free fall Thrown downward Thrown upward

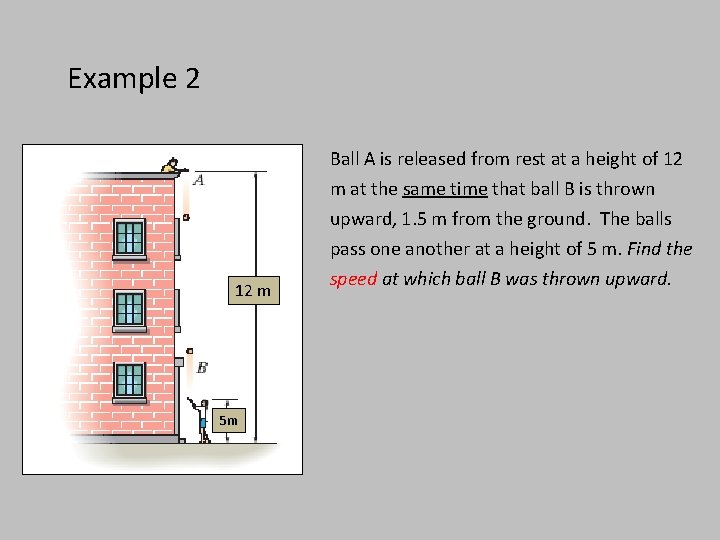
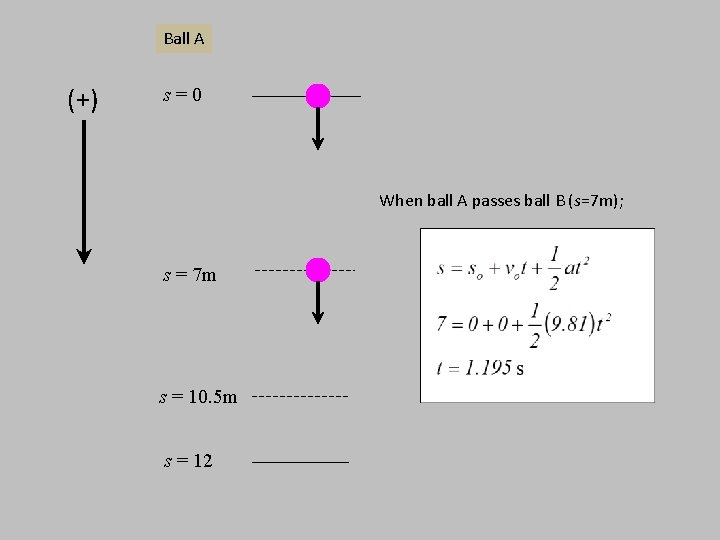
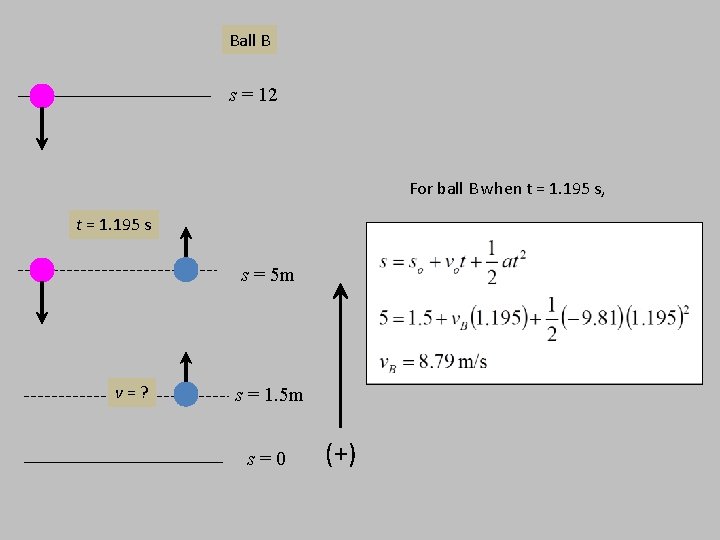
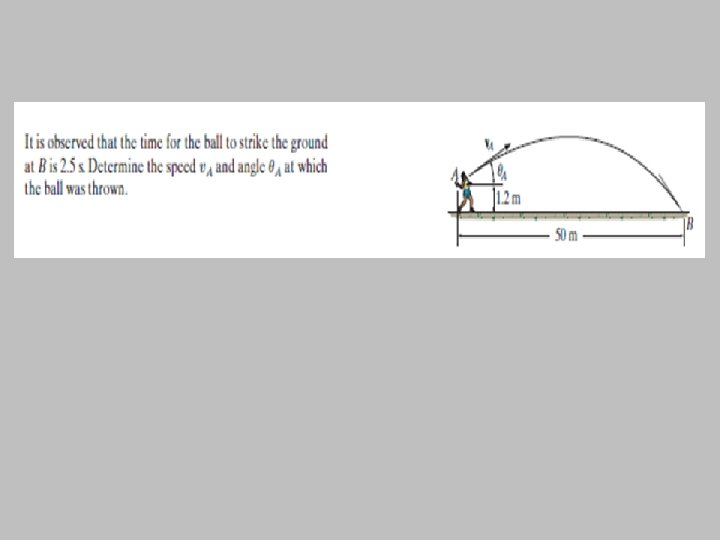
Example 2 Ball A is released from rest at a height of 12 12 m 5 m m at the same time that ball B is thrown upward, 1. 5 m from the ground. The balls pass one another at a height of 5 m. Find the speed at which ball B was thrown upward.

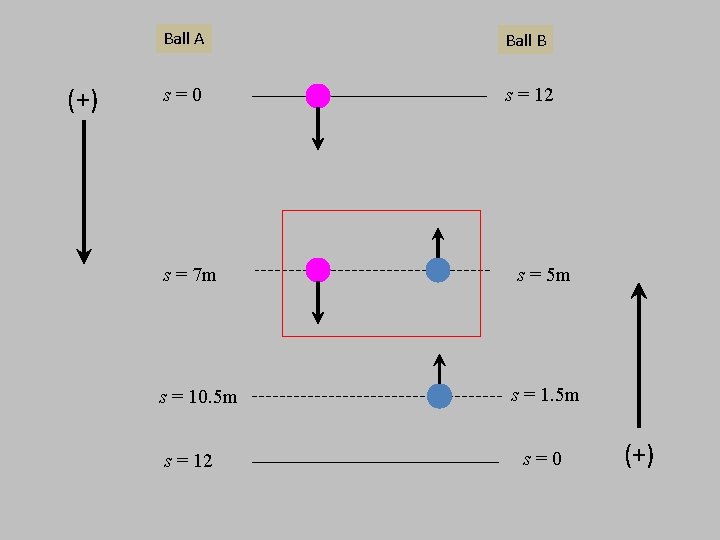
(+) Ball A Ball B s=0 s = 12 s = 7 m s = 10. 5 m s = 12 s = 5 m s = 1. 5 m s=0 (+)

Ball A (+) s=0 When ball A passes ball B (s=7 m); s = 7 m s = 10. 5 m s = 12

Ball B s = 12 For ball B when t = 1. 195 s, t = 1. 195 s s = 5 m v=? s = 1. 5 m s=0 (+)

Erratic motion • When a particle changing its motion ( position, velocity, accelaration). • Cannot be describe as single continous function. • It is convenient to represent the motion in different interval.
![Rectilinear motion so0 vo0 s 1 2 m v 1 0 2 s Rectilinear motion so=0 vo=0 s 1= 2 [m] v 1= 0. 2 s +](https://slidetodoc.com/presentation_image_h2/66956152ec5b0a194ae2ac644636a50b/image-23.jpg)
Rectilinear motion so=0 vo=0 s 1= 2 [m] v 1= 0. 2 s + 3 [m/s] Erratic motion so=0 vo=0 s 1= 2 [m] v 1= 0. 2 s + 3 [m/s] s 2= 4 [m] v 2= 15 [m/s]

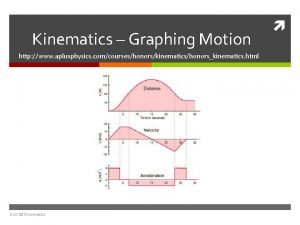
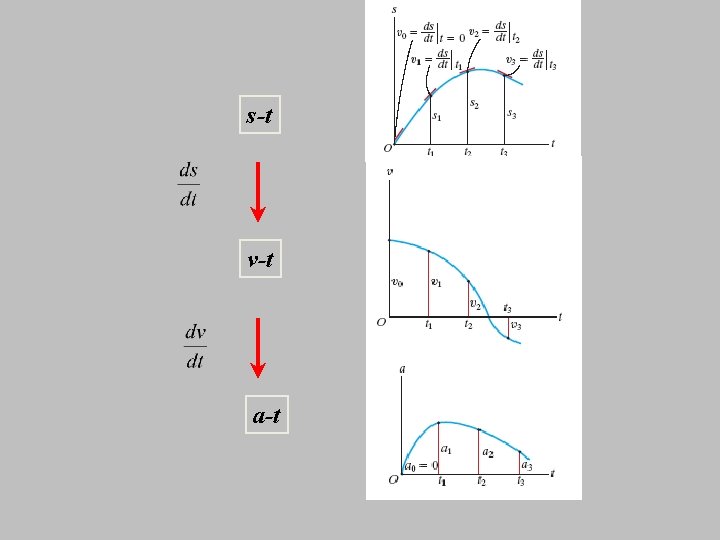
s-t v-t a-t

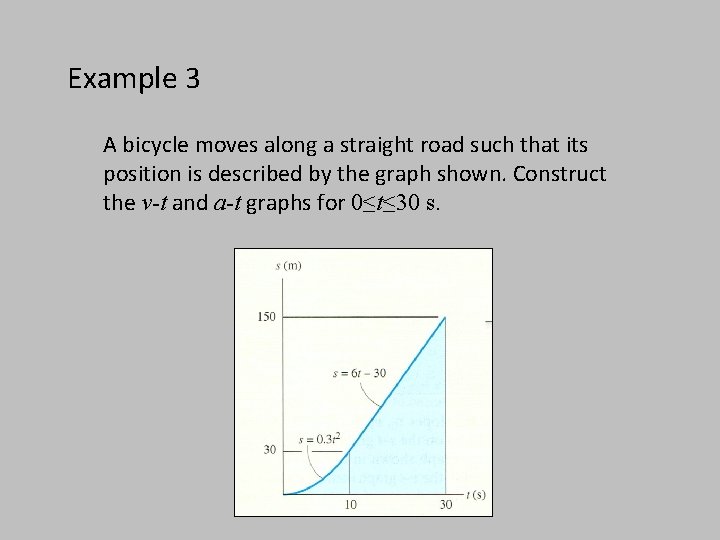
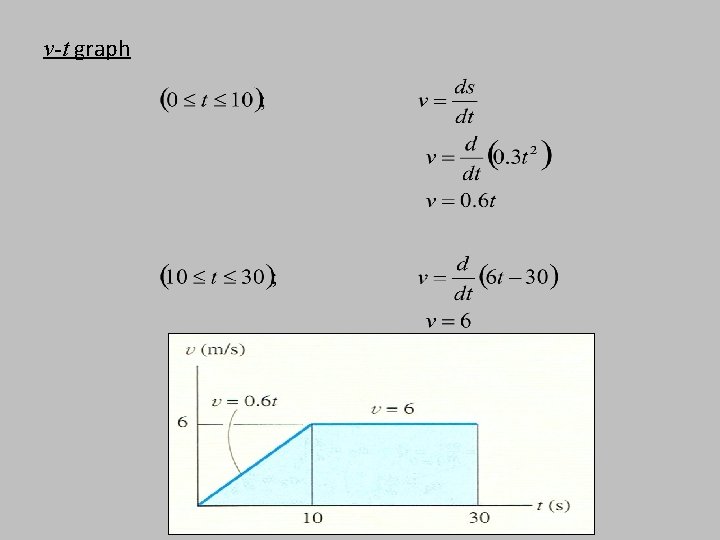
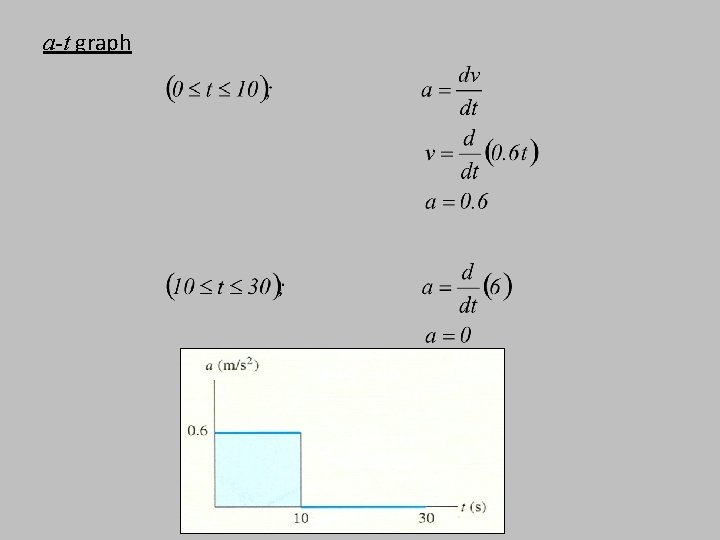
Example 3 A bicycle moves along a straight road such that its position is described by the graph shown. Construct the v-t and a-t graphs for 0≤t≤ 30 s.

v-t graph

a-t graph

a-t v-t s-t

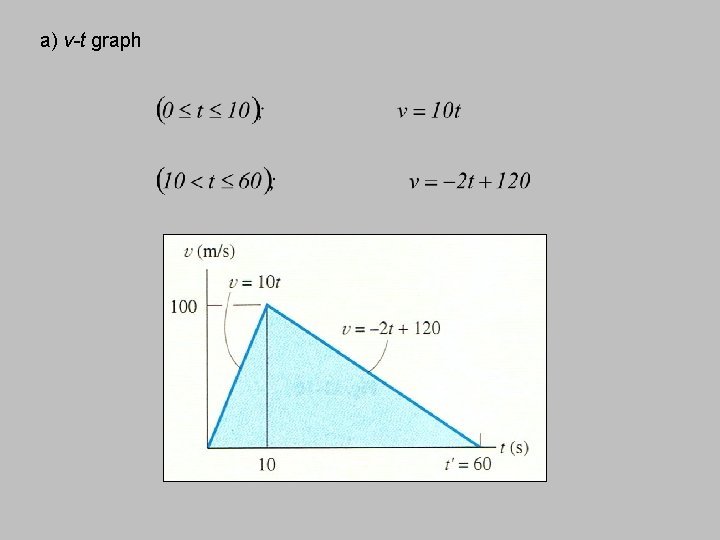
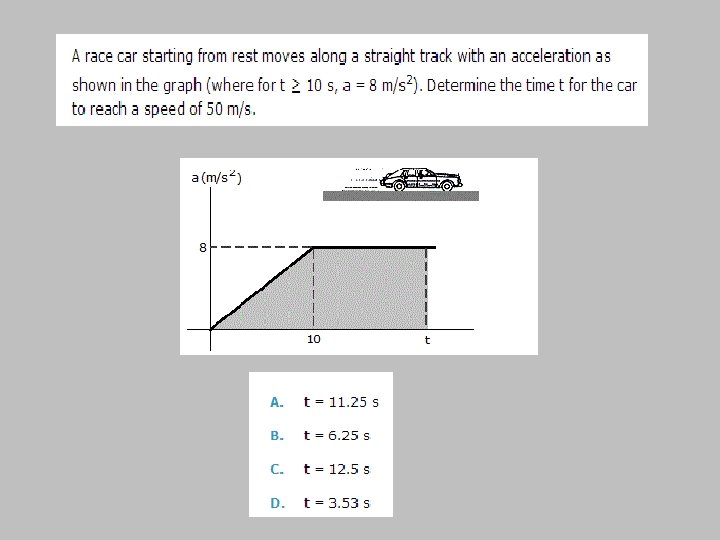
Example 4 The car starts from rest and travels along a straight track such that it accelerates at a constant rate for 10 s and then decelerates at a 2 m/s². a) Draw the v-t and s-t graphs and determine the time t’ needed to stop the car. b) How far has the car traveled?
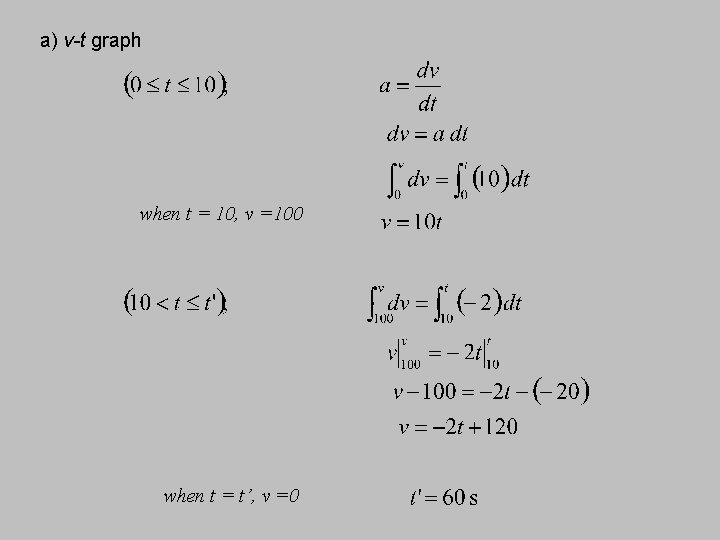
a) v-t graph when t = 10, v =100 when t = t’, v =0

a) v-t graph
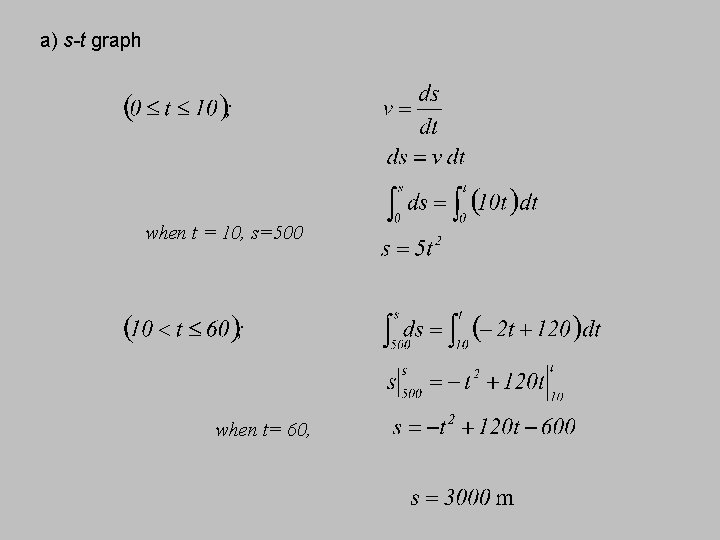
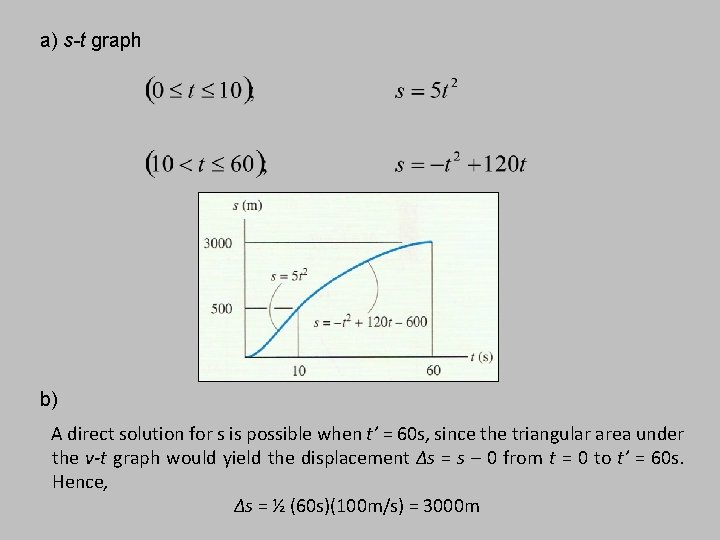
a) s-t graph when t = 10, s=500 when t= 60,

a) s-t graph b) A direct solution for s is possible when t’ = 60 s, since the triangular area under the v-t graph would yield the displacement Δs = s – 0 from t = 0 to t’ = 60 s. Hence, Δs = ½ (60 s)(100 m/s) = 3000 m

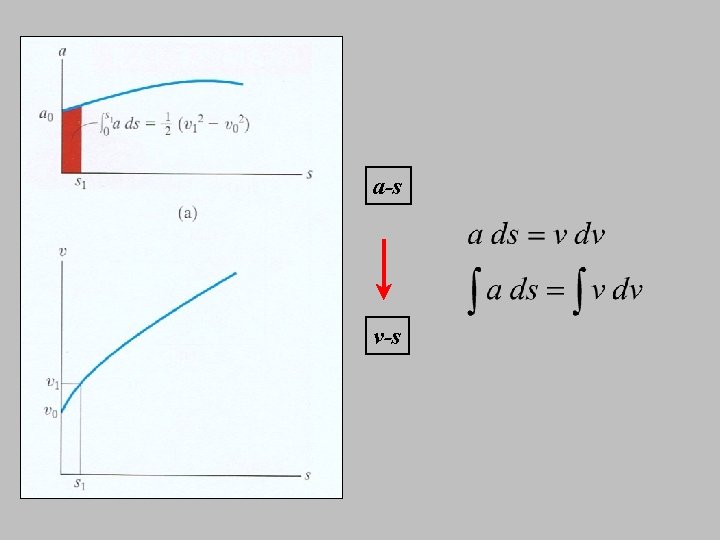
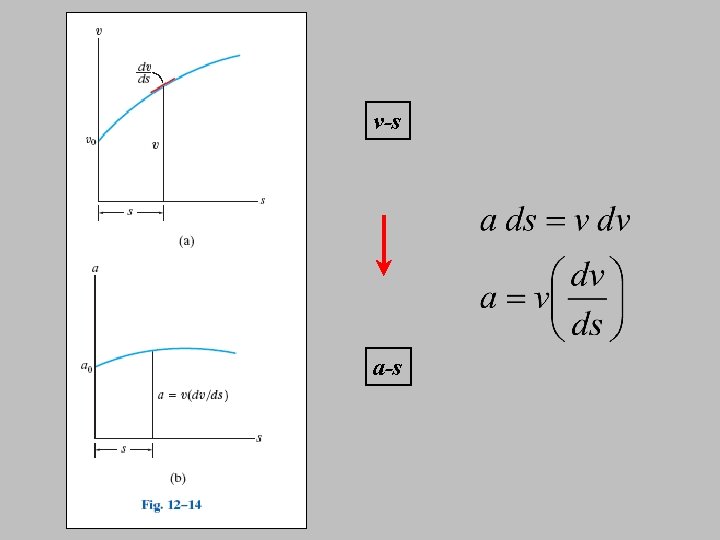
a-s v-s

v-s a-s

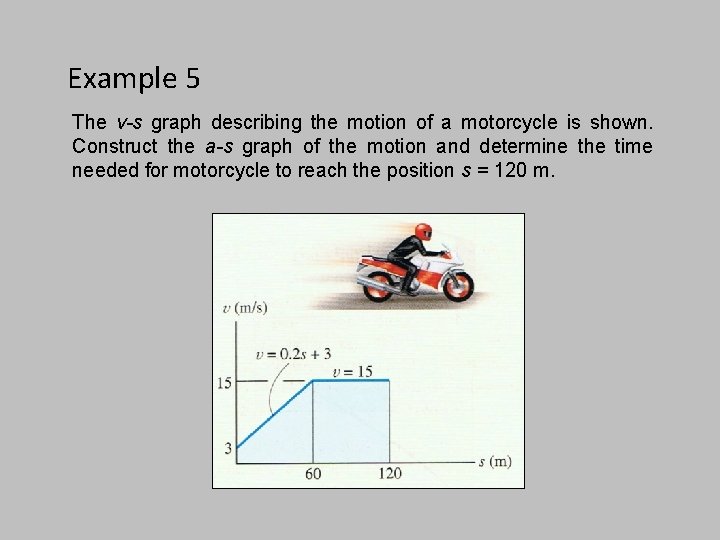
Example 5 The v-s graph describing the motion of a motorcycle is shown. Construct the a-s graph of the motion and determine the time needed for motorcycle to reach the position s = 120 m.
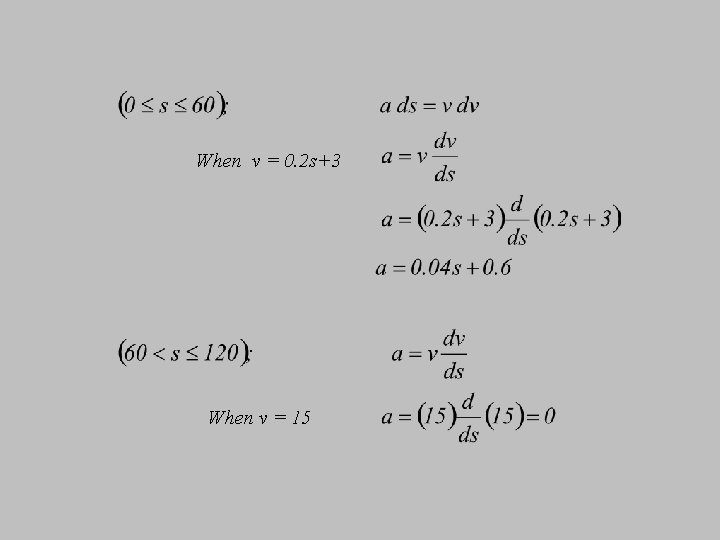
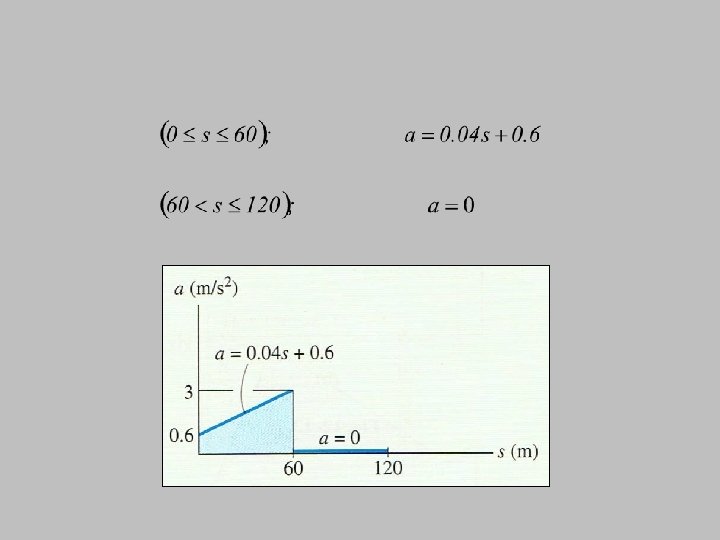
When v = 0. 2 s+3 When v = 15

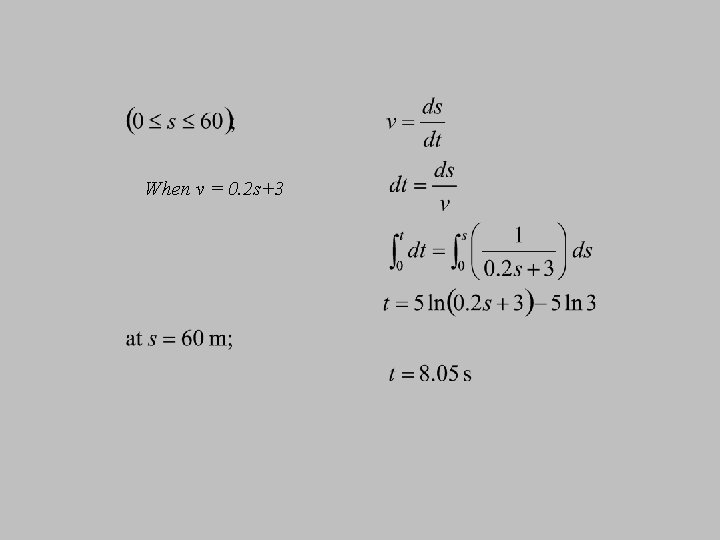
When v = 0. 2 s+3
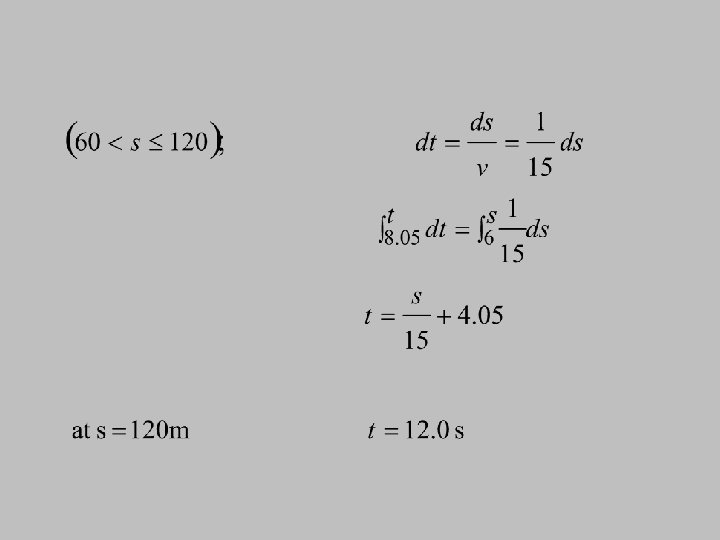


CURVILINEAR MOTION

Curvilinear Motion • Projectile motion • Normal and tangential components


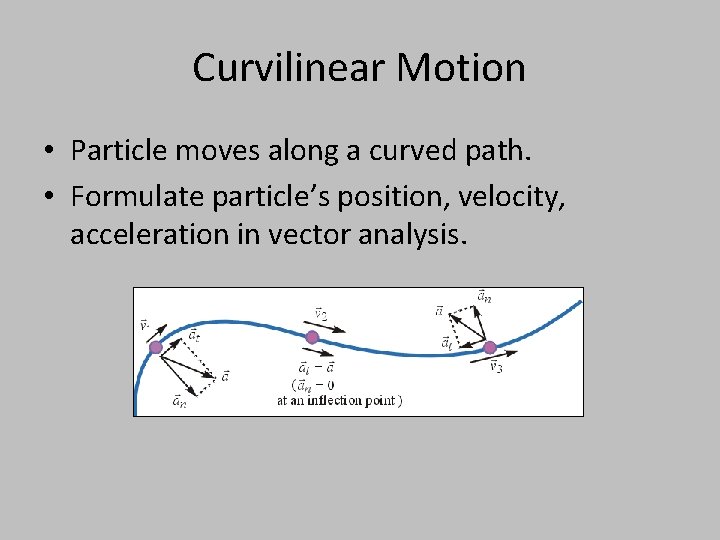
Curvilinear Motion • Particle moves along a curved path. • Formulate particle’s position, velocity, acceleration in vector analysis.

• Projectile Motion • Tangential components

Projectile Motion For a given kick strength, a kicker should know at what angle and initial velocity should the ball be kicked to get the maximum distance and maximum height…

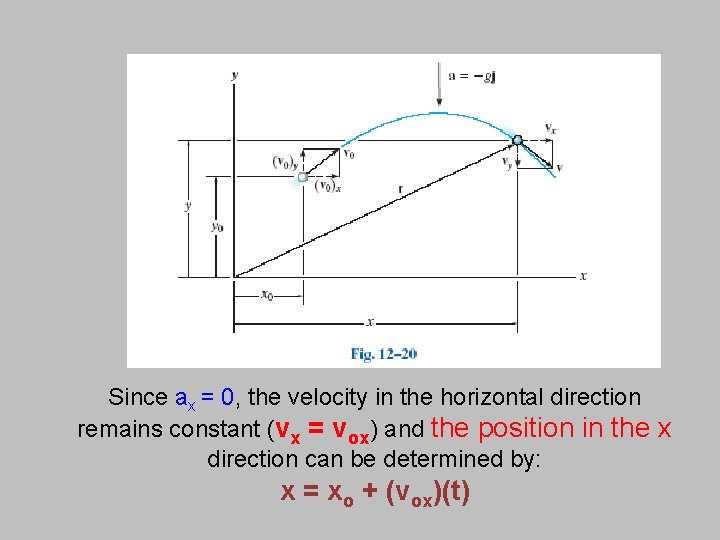
Since ax = 0, the velocity in the horizontal direction remains constant (vx = vox) and the position in the x direction can be determined by: x = xo + (vox)(t)

Horizontal v = v o + a ct a =0 vx = (vo)x s = s o + vo t + a ct 2 x = xo + (vo)xt v 2 = vo 2 + 2 ac(s-so) vx = (vo)x Vertical v = v o + a ct s = s o + v ot + a = - g vy = (vo)y - gt a c t 2 v 2 = vo 2 + 2 ac(s-so) y = yo + (vo)yt - gt 2 vy 2 = (vo)y 2 – 2 g(y-yo)

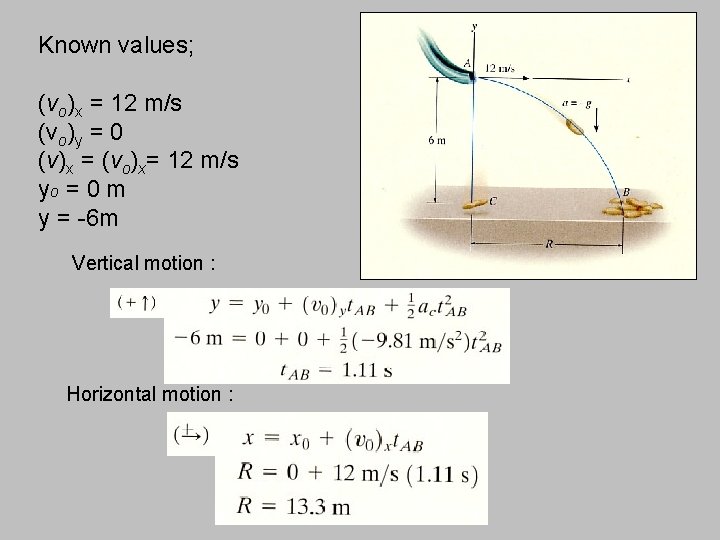
Example 1 A sack slides off the ramp, with a horizontal velocity of 12 m/s. If the height of the ramp is 6 m from the floor, determine : (a) the time needed for the sack to strike the floor, (b) the range R where sacks begin to pile up

Known values; (vo)x = 12 m/s (vo)y = 0 (v)x = (vo)x= 12 m/s yo = 0 m y = -6 m Vertical motion : Horizontal motion :

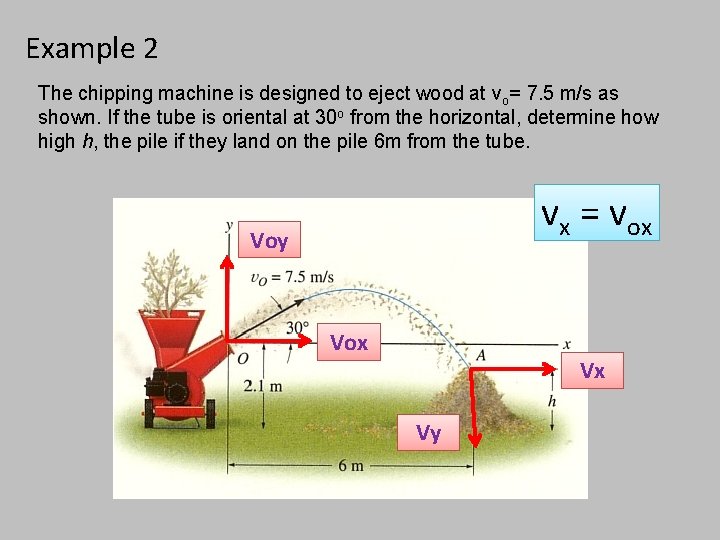
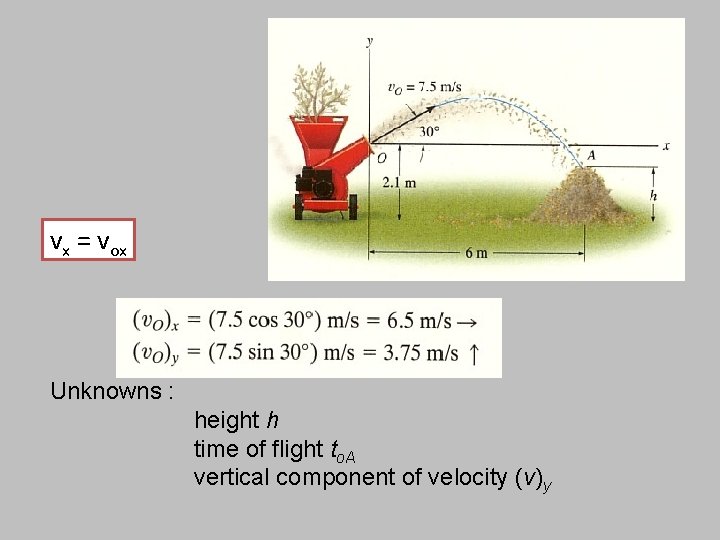
Example 2 The chipping machine is designed to eject wood at vo= 7. 5 m/s as shown. If the tube is oriental at 30 o from the horizontal, determine how high h, the pile if they land on the pile 6 m from the tube. vx = vox Voy Vox Vx Vy

vx = vox Unknowns : height h time of flight to. A vertical component of velocity (v)y

Horizontal Vertical

Normal and tangential motion components

Cars traveling along a cloverleaf interchange experience an acceleration due to a change in speed as well as due to a change in direction of the velocity. If the car’s speed is increasing at a known rate as it travels along a curve, how can we determine the magnitude and direction of its total acceleration?

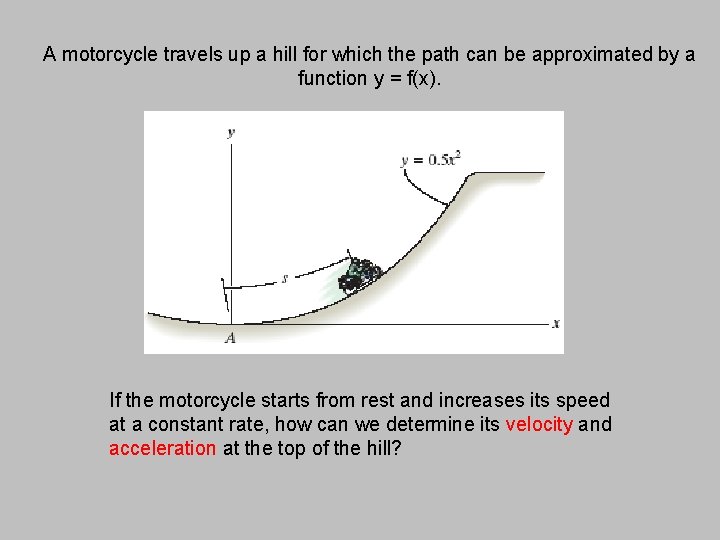
A motorcycle travels up a hill for which the path can be approximated by a function y = f(x). If the motorcycle starts from rest and increases its speed at a constant rate, how can we determine its velocity and acceleration at the top of the hill?

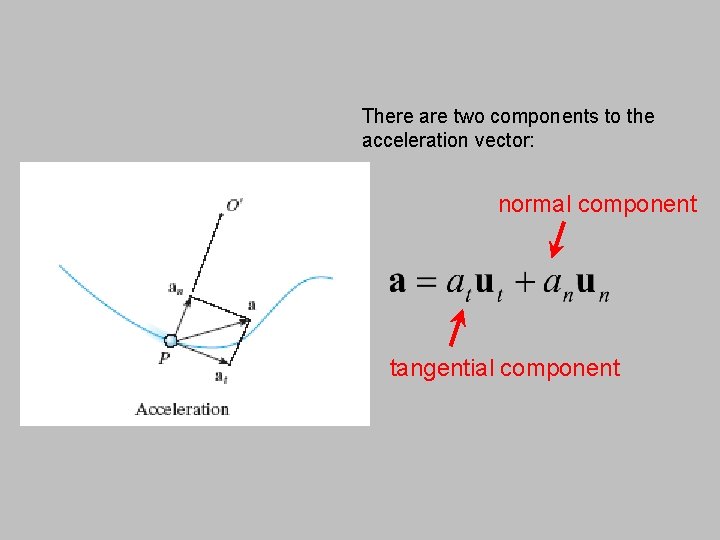
There are two components to the acceleration vector: normal component tangential component

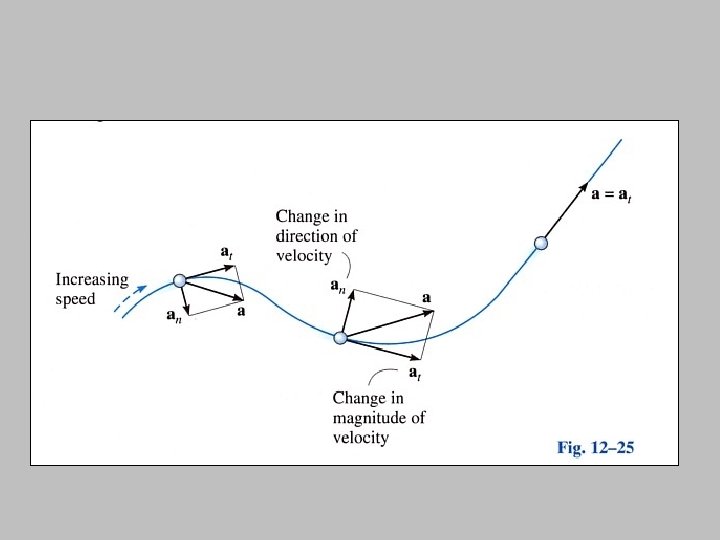
Tangential components • tangent to the curve and in the direction of increasing or decreasing velocity. • represents the time rate of change in the magnitude of the velocity Normal/centripetal components • Always directed toward the center of curvature of the curve. • represents the time rate of change in the direction of the velocity

Consider these two cases: 1. If the particle moves along a straight line 2. If the particle moves along a curve with a constant speed


Constant acceleration

Magnitude of acceleration Radius of curvature

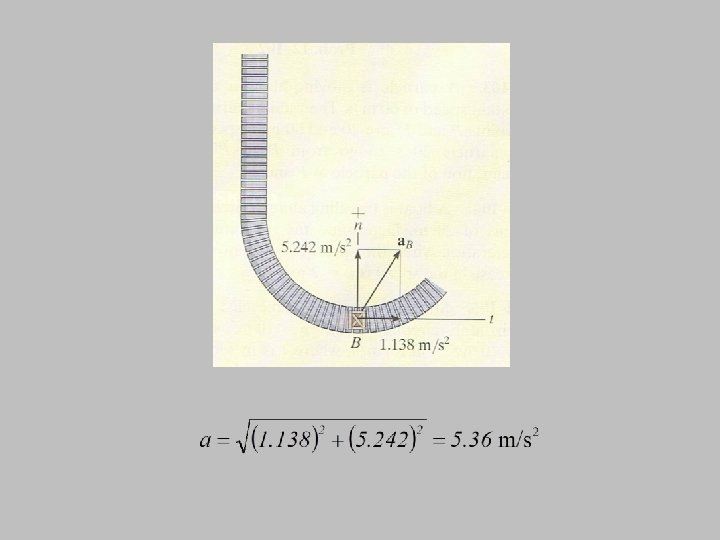
Example 3 The boxes travel along the industrial conveyor. If a box starts from rest at A and increases its speed such that at = (0. 2 t) m/s 2, determine the magnitude of its acceleration when it arrives at point B.

magnitude of acceleration at B; Have to find t first by using known S (distance) Known;

distance from A to B; to find t. B

At point B;




 Chapter 12 kinematics of a particle solutions
Chapter 12 kinematics of a particle solutions Aplusphysics kinematics-horizontal kinematics
Aplusphysics kinematics-horizontal kinematics Kinematics of a particle moving in a straight line answers
Kinematics of a particle moving in a straight line answers Kinematics of a particle
Kinematics of a particle Kinematics of a particle
Kinematics of a particle Tricycle kinematics
Tricycle kinematics What is kinematics
What is kinematics Sin 37°
Sin 37° Rotational kinematics
Rotational kinematics Angular kinematic variables
Angular kinematic variables Plane kinematics of rigid bodies
Plane kinematics of rigid bodies Omni projectile motion calculator
Omni projectile motion calculator Range motion
Range motion Dr frost further kinematics
Dr frost further kinematics Equation of kinematics
Equation of kinematics Kinematic equaitons
Kinematic equaitons Instantaneous velocity
Instantaneous velocity Transport theorem kinematics
Transport theorem kinematics Closed form solutions
Closed form solutions Jacobian singularity
Jacobian singularity Introduction to physics ppt free download
Introduction to physics ppt free download Rectilinear kinematics continuous motion
Rectilinear kinematics continuous motion Rectilinear kinematics
Rectilinear kinematics Rtt fluid mechanics
Rtt fluid mechanics Kinematics ppt
Kinematics ppt Coriolis acceleration
Coriolis acceleration Kinematic of rigid body
Kinematic of rigid body Fluid statics ppt
Fluid statics ppt Magnitude of angular acceleration formula
Magnitude of angular acceleration formula Linear and angular kinematics
Linear and angular kinematics Forward kinematics
Forward kinematics What is erratic motion
What is erratic motion Fbd and kd
Fbd and kd Nmt.ee
Nmt.ee The ticker tape case graph
The ticker tape case graph Aplusphysics kinematics-free fall answers
Aplusphysics kinematics-free fall answers Inverse kinematics
Inverse kinematics What is continuous motion in dynamics
What is continuous motion in dynamics Planar kinematics of a rigid body
Planar kinematics of a rigid body Dh parameters
Dh parameters A tourist being chased by an angry bear
A tourist being chased by an angry bear General plane motion
General plane motion Curvilinear translation
Curvilinear translation Angular kinematics biomechanics
Angular kinematics biomechanics Suvat equations questions
Suvat equations questions A level physics kinematics
A level physics kinematics Salmon often jump waterfalls to reach
Salmon often jump waterfalls to reach Kinematic equations rearranged
Kinematic equations rearranged Ib physics
Ib physics Kinematics of simple harmonic motion
Kinematics of simple harmonic motion One dimensional kinematics problems
One dimensional kinematics problems Linear kinematics examples
Linear kinematics examples Aplusphysics kinematics-free fall answers
Aplusphysics kinematics-free fall answers Spherical wrist
Spherical wrist Introduction of kinematics
Introduction of kinematics Apertura numerica
Apertura numerica Graphical integration in motion analysis
Graphical integration in motion analysis What is motion along a straight line
What is motion along a straight line Rotational kinematics
Rotational kinematics 3 body decay
3 body decay Arnold kennedy theorem
Arnold kennedy theorem Robot path
Robot path Kinematics
Kinematics Kinematics
Kinematics Body kinematics
Body kinematics Lathe
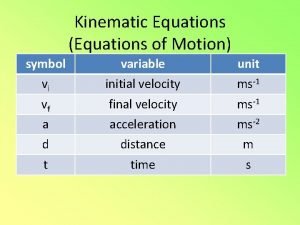
Lathe Kinematics symbols
Kinematics symbols Kinematics
Kinematics Describing motion kinematics in one dimension
Describing motion kinematics in one dimension Describing motion kinematics in one dimension
Describing motion kinematics in one dimension Kinematics
Kinematics Kinematics physics
Kinematics physics