OPERATOR FORMALISM OF QUANTUM MECHANICS Dr N Shanmugam







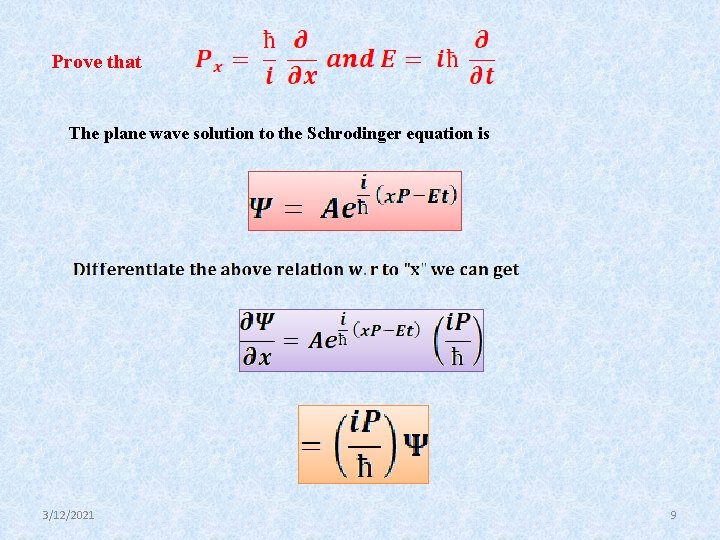









![Commuting operator Therefore AB – BA = 0 [A, B] = 0 Anti commuting Commuting operator Therefore AB – BA = 0 [A, B] = 0 Anti commuting](https://slidetodoc.com/presentation_image_h/3609aa4f42f6459264275d4baaad7e1b/image-20.jpg)







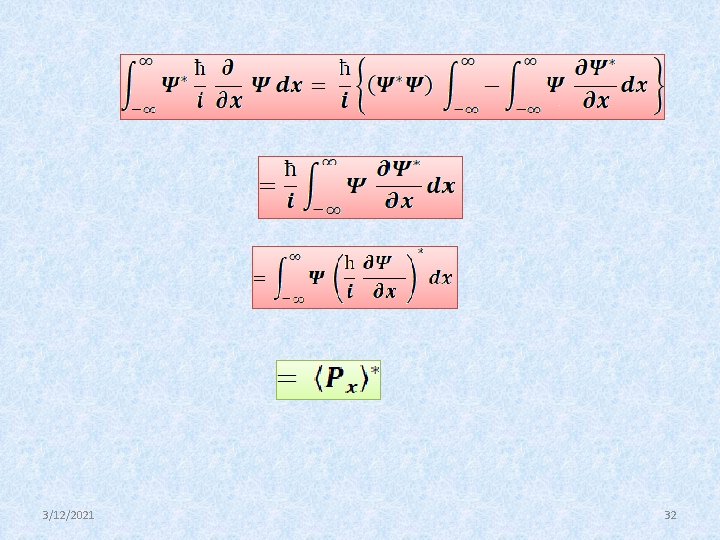


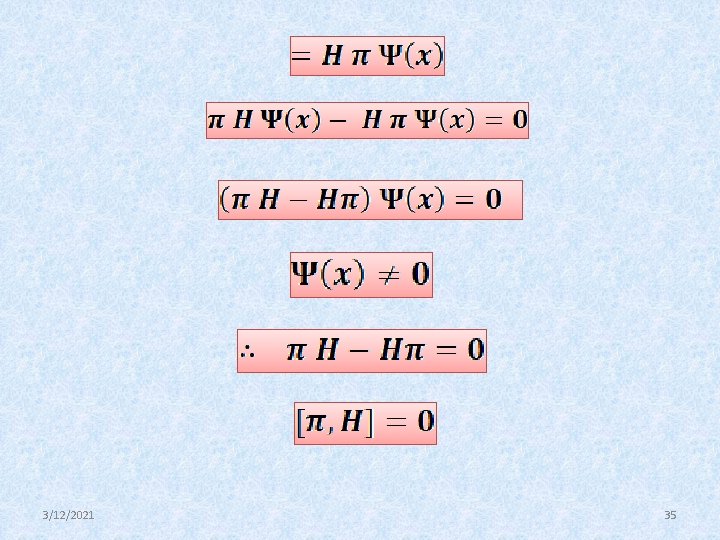

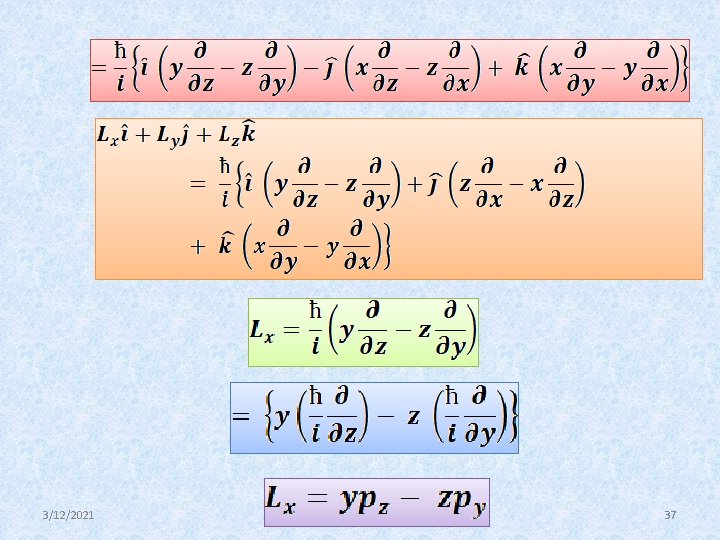
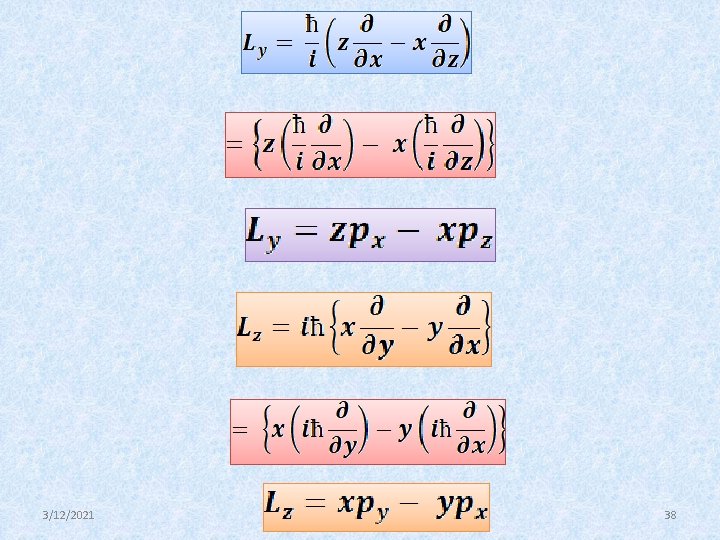


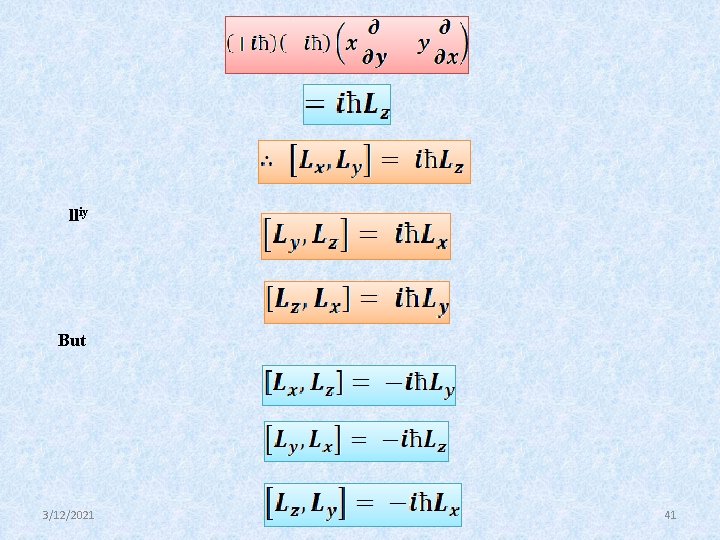

![We know that [AB, C] = [A, C]B + A[B, C] In the same We know that [AB, C] = [A, C]B + A[B, C] In the same](https://slidetodoc.com/presentation_image_h/3609aa4f42f6459264275d4baaad7e1b/image-43.jpg)




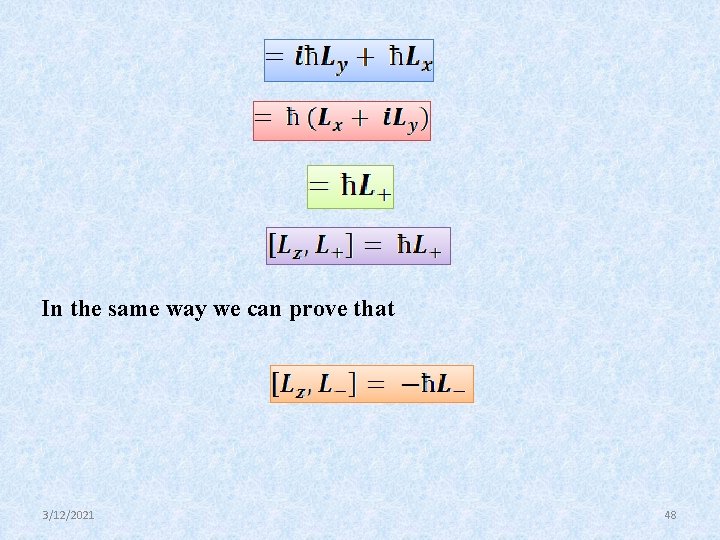

- Slides: 49

OPERATOR FORMALISM OF QUANTUM MECHANICS Dr. N. Shanmugam ASSISTANT PROFESSOR 3/12/2021 DEPARTMENT OF PHYSICS ANNAMALAI UNIVERSITY DEPUTED TO D. G. Govt. Arts college (W) 1 Mayiladuthurai-609001

WHAT IS AN OPERATOR? v. Operator is a mathematical quantity when it operates on one function, it charges the function into another one and some times leave the function unaffected. v. Examples of operators are addition, subtraction, multiplication, division, differentiation, integration, operations of grad, div, curl etc. 3/12/2021 2

WHY WE NEED AN OPERATOR? v According to Heisenberg’s uncertainty principle, some physical quantities like position, momentum, energy, time, etc cannot be measured beyond a certain degree of accuracy in quantum mechanics. Therefore, the physical variables are given in terms of the average value. To determine the average of physical quantities, some suitable operators are used. 3/12/2021 3

EXPECTATION VALUE v. Among the so many measurements made on a single dynamical variable, most of the time we can get a particular value called the expectation value. 3/12/2021 4

The expectation value of an operator A is 3/12/2021 5

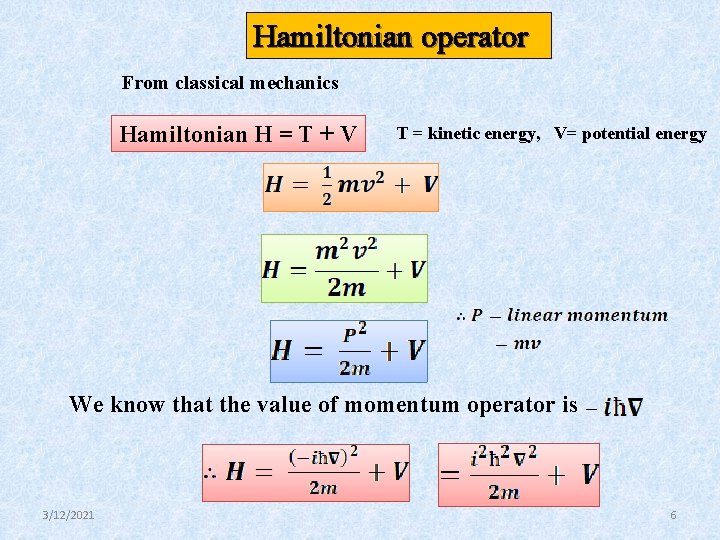
Hamiltonian operator From classical mechanics Hamiltonian H = T + V T = kinetic energy, V= potential energy We know that the value of momentum operator is 3/12/2021 6

Free particle Hamiltonian For a free particle V=0 3/12/2021 7

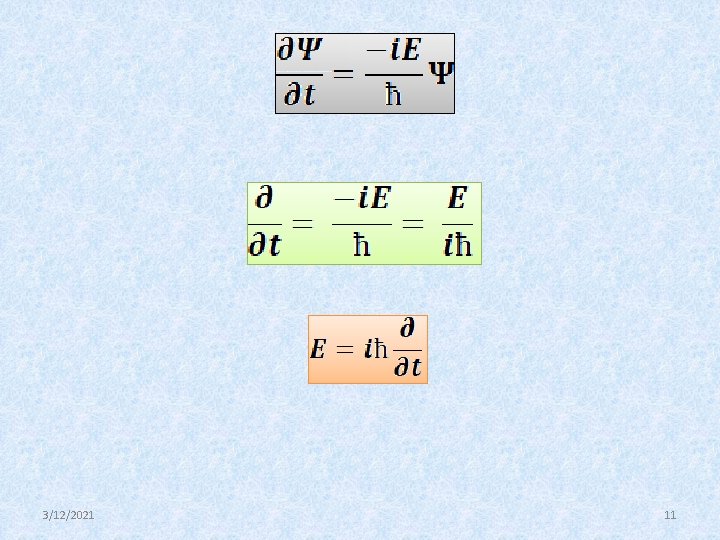
(Time Independent Schrodinger Equation) E= Energy Eigenvalue (Time dependent Schrodinger Equation) 3/12/2021 8
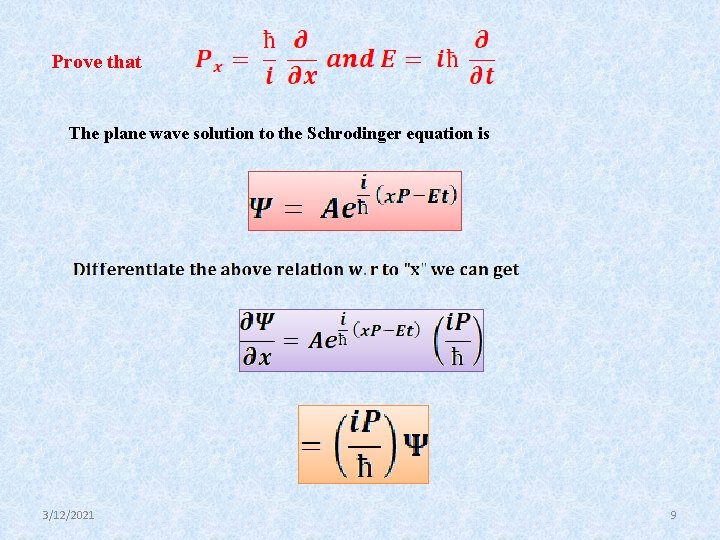
Prove that The plane wave solution to the Schrodinger equation is 3/12/2021 9

or 3/12/2021 10

3/12/2021 11

3/12/2021 12

Eigenvalue equation is 3/12/2021 3: 25 AM 13

3/12/2021 14

Identity (or) Unity operator Null operator 3/12/2021 15

Inverse operator -1 (or) = -1 and -1 -1 = are inverse operators. Equal operator 3/12/2021 16

Parity operator The parity operator is a special mathematical operator and is denoted by. For a wave function of the variable x, The parity operator is defined as is operated This means that when the wavefunction by the parity operator, it gets reflected in its co-ordinates. 3/12/2021 17

, Eigenvalue of parity operator The Eigenvalue equation of the parity operator is Operating the above equation again by This means that is the parity operator is operated twice Hence, 3/12/2021 18

Therefore, the Eigenvalues are +1 and -1. From the equations 1 and 2 If λ =1, the wave function is even If λ = -1, the wave function is add Bosans are described by symmetric wave function. Fermions are described by symmetric wave function. 3/12/2021 19
![Commuting operator Therefore AB BA 0 A B 0 Anti commuting Commuting operator Therefore AB – BA = 0 [A, B] = 0 Anti commuting](https://slidetodoc.com/presentation_image_h/3609aa4f42f6459264275d4baaad7e1b/image-20.jpg)
Commuting operator Therefore AB – BA = 0 [A, B] = 0 Anti commuting operator ie AB + BA =0 3/12/2021 20

Linear operator An operator is said to be linear if it satisfies the relation where C 1 and C 2 are constants. The inverse operator A-1 is defined by the relation An operator commutes with its inverse 3/12/2021 21

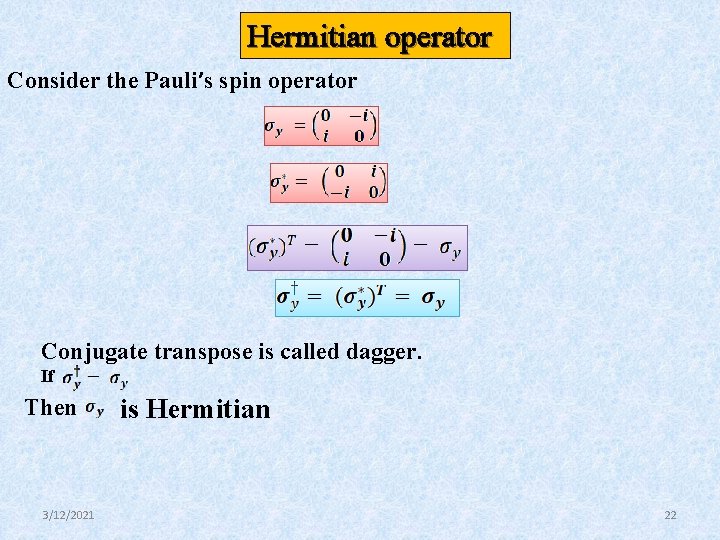
Hermitian operator Consider the Pauli’s spin operator Conjugate transpose is called dagger. If Then 3/12/2021 is Hermitian 22

An operator is said to be Hermitian if satisfy the following condition. 3/12/2021 =A and it should 23

For any operator A (a) Hermitian, (b) anti Hermitian, (c) unitary, (d) orthogonal 3/12/2021 24

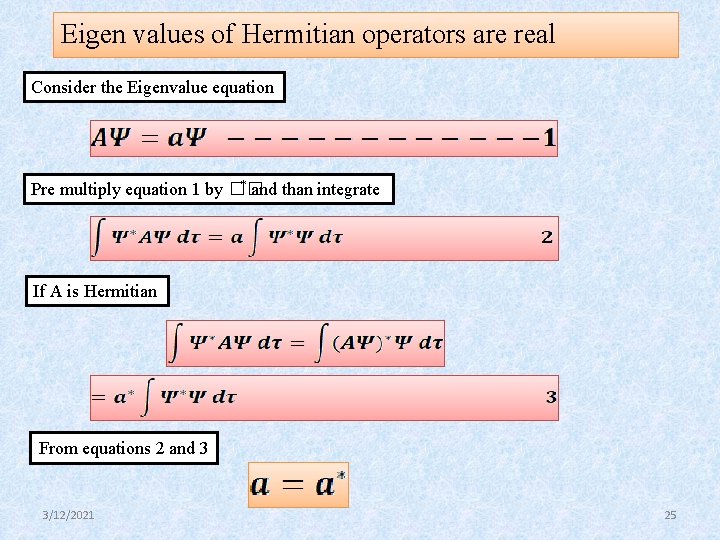
Eigen values of Hermitian operators are real Consider the Eigenvalue equation * and than integrate Pre multiply equation 1 by �� If A is Hermitian From equations 2 and 3 3/12/2021 25

Two Eigenfunctions of Hermitian operators, belonging to different Eigenvalues, are orthogonal Consider �� , and �� are the two Eigenfunctions of the Hermitian operator. There we can write * and then integrate, we can get Pre multiply equation 1 by �� If A is Hermitian 3/12/2021 26

3 -4 ⇒ From equation 5, it is clear that (a-b) ≠ 0 should be equal to zero. This means that the i. e a ≠ b, but wavefunctions �� and �� are mutually orthogonal. 3/12/2021 27

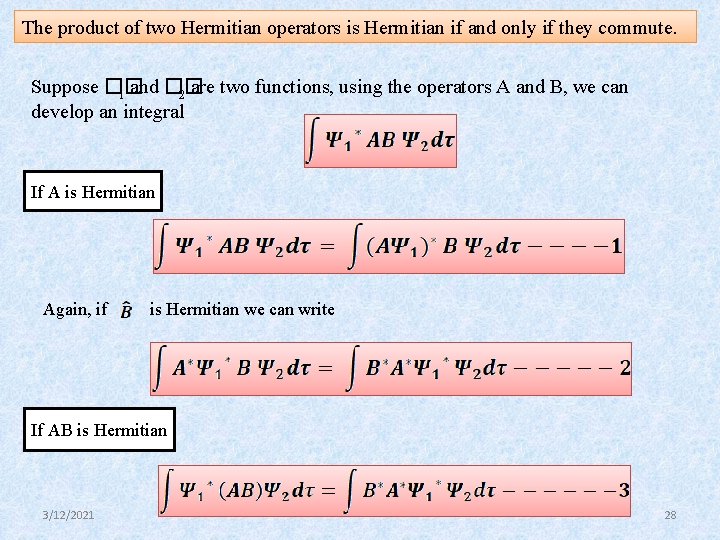
The product of two Hermitian operators is Hermitian if and only if they commute. Suppose �� 1 and �� 2 are two functions, using the operators A and B, we can develop an integral If A is Hermitian Again, if is Hermitian we can write If AB is Hermitian 3/12/2021 28

If the operators A and B commute, we have Which is the condition for the product operator to be Hermitian 3/12/2021 29

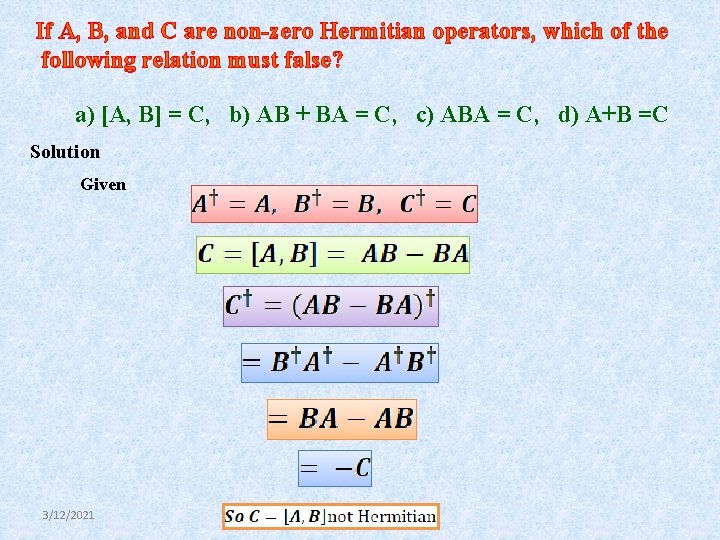
If A, B, and C are non-zero Hermitian operators, which of the following relation must false? a) [A, B] = C, b) AB + BA = C, c) ABA = C, d) A+B =C Solution Given + 3/12/2021

Prove that the momentum operator is Hermitian Momentum operator If P is said to be Hermitian The expectation value of can be written as We have to solve the above integral Put 3/12/2021 31
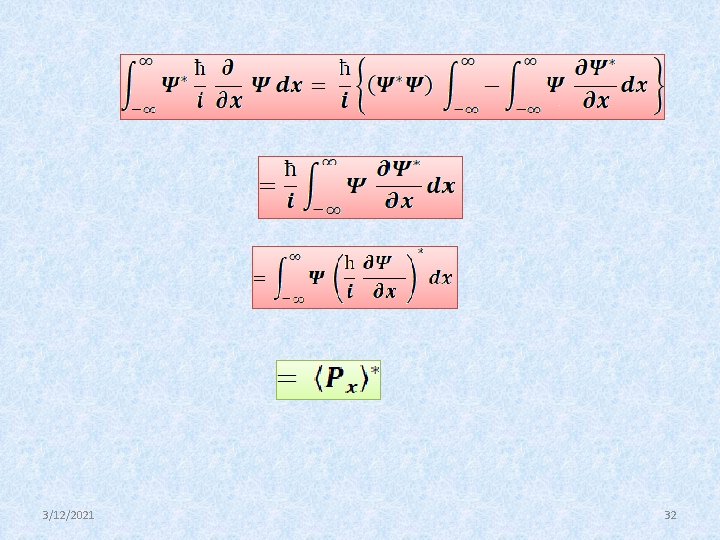
3/12/2021 32

Prove that parity operator commutes with the Hamiltonian π = Parity operator H = Total Hamiltonian We have to prove [π, H] = 0 ie πH = H π πH - H π = 0 we know that 3/12/2021 33

3/12/2021 34
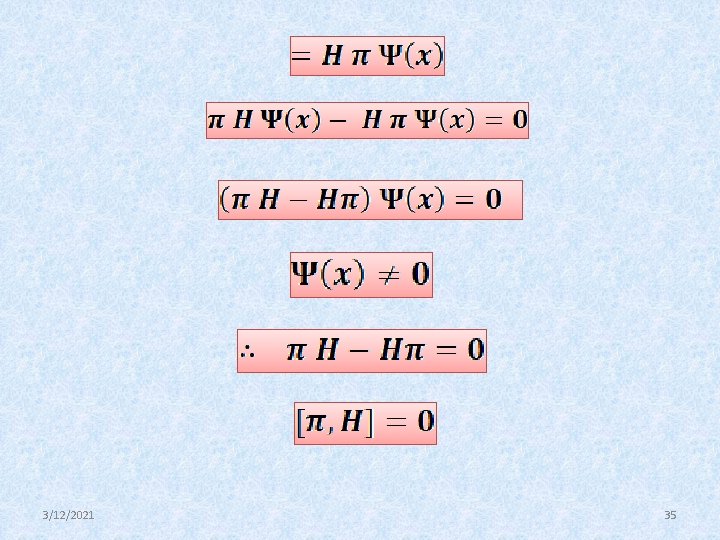
3/12/2021 35

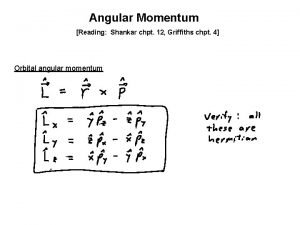
Angular momentum operators We know that the orbital angular momentum 3/12/2021 36
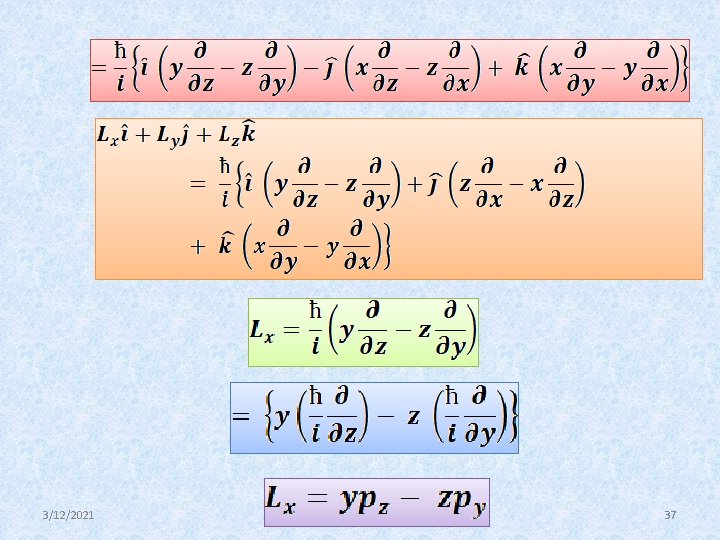
3/12/2021 37
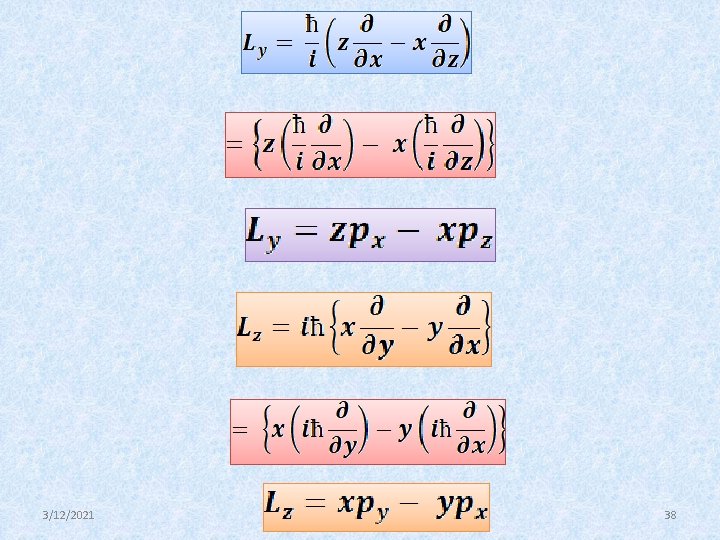
3/12/2021 38

3/12/2021 39

3/12/2021 40
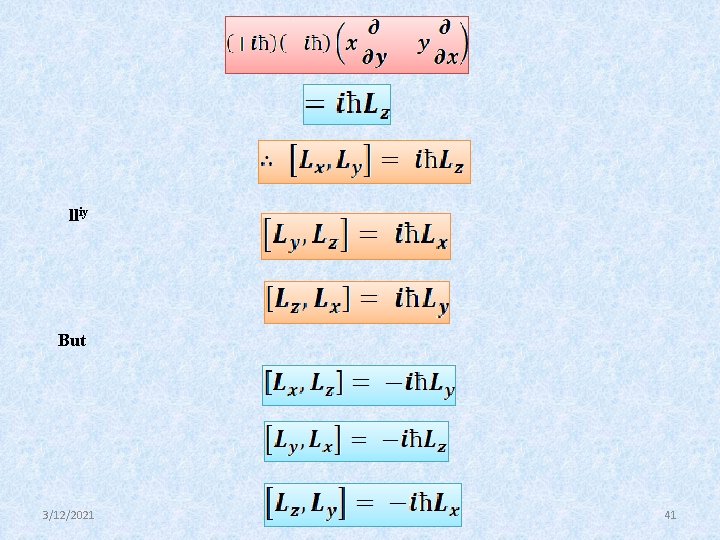
lliy But 3/12/2021 41

Value of Commutation relation between L 2 and Lz 3/12/2021 42
![We know that AB C A CB AB C In the same We know that [AB, C] = [A, C]B + A[B, C] In the same](https://slidetodoc.com/presentation_image_h/3609aa4f42f6459264275d4baaad7e1b/image-43.jpg)
We know that [AB, C] = [A, C]B + A[B, C] In the same way we can prove that ------1 3/12/2021 43

-------2 From the equations 1 and 2 We may conclude that the square of the angular momentum operator commutes with one of its components but the components among themselves do not commute. 3/12/2021 44

Raising and Lowering operators (Ladder operators) are called raising. and lowering operators, repectively. Each time operation of the raising operator may increase the Eigenvalue of the system by one unit of ћ On the other hand, each time operation of lowering operator may decrease the Eigenvalue of the system by one unit of ћ. Therefore, these operators are called Ladder operators. 3/12/2021 45

Commutation relation between Similarly 3/12/2021 46

Commutation relation between 3/12/2021 47
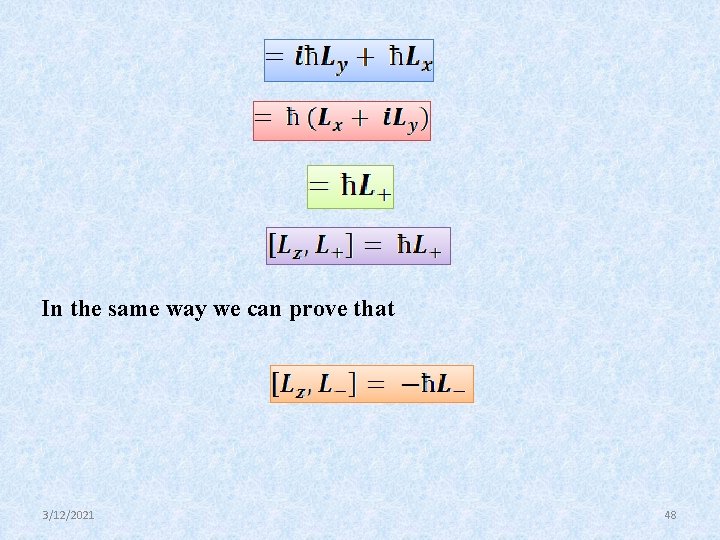
In the same way we can prove that 3/12/2021 48

3/12/2021 49
 Operators in quantum mechanics
Operators in quantum mechanics Edict pharmaceuticals
Edict pharmaceuticals Classical mechanics
Classical mechanics Quantum physics vs mechanics
Quantum physics vs mechanics Operator in quantum mechanics
Operator in quantum mechanics New criticism and formalism differences
New criticism and formalism differences Logical operators priority in c
Logical operators priority in c Unary and binary operator
Unary and binary operator Pada tipe data boolean berlaku operator-operator adalah
Pada tipe data boolean berlaku operator-operator adalah Pada tipe data boolean, berlaku operator-operator...
Pada tipe data boolean, berlaku operator-operator... Completeness in quantum mechanics
Completeness in quantum mechanics Littlejohn quantum mechanics
Littlejohn quantum mechanics Introduction to quantum statistical mechanics
Introduction to quantum statistical mechanics Quantum mechanics basics
Quantum mechanics basics Dr susan cartwright
Dr susan cartwright Quantum mechanics definition
Quantum mechanics definition Wave reflection formula
Wave reflection formula Review of quantum mechanics
Review of quantum mechanics Expectation value in quantum mechanics
Expectation value in quantum mechanics Postulates of quantum mechanics
Postulates of quantum mechanics Quantum mechanics powerpoint
Quantum mechanics powerpoint What is the prison program quantum mechanics
What is the prison program quantum mechanics Quantum mechanics
Quantum mechanics Schröndiger
Schröndiger Postulates of quantum mechanics
Postulates of quantum mechanics Expectation value of energy in quantum mechanics
Expectation value of energy in quantum mechanics Griffiths
Griffiths Mathematical tools of quantum mechanics
Mathematical tools of quantum mechanics Spin 1 operators
Spin 1 operators Central potential quantum mechanics
Central potential quantum mechanics Commutation relation in quantum mechanics
Commutation relation in quantum mechanics Hermitian operator
Hermitian operator Commutation relation in quantum mechanics
Commutation relation in quantum mechanics Ap physics quantum mechanics
Ap physics quantum mechanics Quantum mechanics in your face
Quantum mechanics in your face Finite potential well
Finite potential well Transfer matrix quantum mechanics
Transfer matrix quantum mechanics French and taylor quantum mechanics
French and taylor quantum mechanics Quantum mechanics in three dimensions
Quantum mechanics in three dimensions Operators in quantum mechanics
Operators in quantum mechanics Quantum mechanics
Quantum mechanics Expectation value of energy in quantum mechanics
Expectation value of energy in quantum mechanics Rigid rotor quantum mechanics
Rigid rotor quantum mechanics Qft
Qft Quantum mechanics postulate
Quantum mechanics postulate Russian formalism theory
Russian formalism theory 4 critical variables of literary theory and criticism
4 critical variables of literary theory and criticism Approaches formalism and substantivism
Approaches formalism and substantivism Formalism ethics
Formalism ethics Formalist lens
Formalist lens